NIPS17 GNN GraphSAGE 论文解读

论文链接：https://arxiv.org/pdf/1706.02216v1.pdf

论文代码：Pytorch Geometric实现

概括

Low-dimensional embeddings of nodes in large graphs have proved extremely useful in a variety of prediction tasks, from content recommendation to identifying protein functions。However, most existing approaches require that all nodes in the graph are present during training of the embeddings; these previous approaches are inherently transductive and do not naturally generalize to unseen nodes。Here we present GraphSAGE, a general inductive framework that leverages node feature information (e.g., text attributes) to efficiently generate node embeddings for previously unseen data。Instead of training individual embeddings for each node, we learn a function that generates embeddings by sampling and aggregating features from a node’s local neighborhood。Our algorithm outperforms strong baselines on three inductive node-classification benchmarks: we classify the category of unseen nodes in evolving information graphs based on citation and Reddit post data, and we show that our algorithm generalizes to completely unseen graphs using a multi-graph dataset of protein-protein interactions

大多数现有的方法都要求在嵌入训练期间，图的所有节点都存在；这些以前的方法本质上是直推式(Transductive Learning)的，不能自然地推广到看不见的节点。这里我们展示了GraphSAGE，这是一个通用的归纳框架，它利用节点特征信息（例如，文本属性）高效地为新的数据生成节点嵌入。我们没有为每个节点训练单个嵌入，而是学习一个函数，该函数通过从节点的局部邻域采样和聚合特征来生成嵌入。

1. 前言

节点嵌入法的基本思想是利用降维技术将节点图邻域的高维信息提取到密集向量嵌入中。然后可以将这些节点嵌入反馈到下游机器学习系统，并帮助完成节点分类、聚类和链接预测等任务。

然后，现有的工作都关注于单个固定图中的节点嵌入，许多现实世界的应用程序需要为看不见的节点或全新图快速生成嵌入。这种归纳能力(Inductive Learning)对于高通量、生产型机器学习系统至关重要，这些系统在不断变化的图形上运行，并不断遇到看不见的节点（例如Reddit上的帖子、用户和Youtube上的视频）。生成节点嵌入的归纳方法也有助于在具有相同特征形式的图之间进行泛化：例如，可以在从模型生物衍生的蛋白质-蛋白质相互作用图上训练嵌入生成器，然后使用训练过的模型轻松生成新生物上收集的数据的节点嵌入。

即，以前的图网络(GCN)，需要得到整张图才能训练或预测，无法对未知数据预测。本文针对这个问题，将图的训练改为对节点的嵌入学习

直推式学习(Transductive Learning)：GCN

归纳学习(Inductive Learning)：GraphSAGE

与Transductive Learning相比，Inductive Learning的节点嵌入问题尤其困难，因为推广到看不见的节点需要将新观察到的子图与算法已经优化的节点嵌入“对齐”。归纳框架必须学会识别节点邻域的结构属性，这些属性揭示了节点在图中的局部角色及其全局位置。

大多数现有的生成节点嵌入的方法本质上是直推式的。这些方法中的大多数使用基于矩阵分解的目标直接优化每个节点的嵌入，并且不会自然地推广到看不见的数据，因为它们在单个固定图中对节点进行预测。这些方法可以修改为在归纳环境中运行，但这些修改往往在计算上很昂贵，需要在进行新预测之前进行额外的梯度下降。最近也有一些使用卷积算子学习图结构的方法，它们有望成为一种嵌入方法。到目前为止，图卷积网络（GCN）仅应用于固定图的直推式。在这项工作中，我们将GCN扩展到归纳无监督学习的任务，并提出了一个框架，将GCN方法推广到使用可训练的聚合函数。

问：为什么GCN就是Transductive的，而GraphSAGE就是Inductive的？

回答：训练好的GCN唯一的参数就是W，当W训练好后按理说加入新的节点，或预测新的图，只是聚合周围节点信息，再用W转换特征向量的过程，是可以被理解为Inductive的。个人理解，GraphSAGE的出发点就是说，传统的基于频谱的图网络，需要每次计算图的邻接矩阵和度矩阵，当有新节点加入时，其laplace矩阵也会发生变化，对结果有一定影响。而GraphSAGE只需要周围节点的信息就可以训练或得到新节点的嵌入，新节点的出现对结果没有影响。

但：我觉得说不通，GCN也能将新节点加入并预测，只需要改动邻接矩阵即可。并且之后也有论文针对GCN做Inductive的实验，也是能够预测的。姑且以GraphSAGE论文出发点继续往下读吧。

频谱域方法：GCN需要利用邻接矩阵和度矩阵构造laplace矩阵的方法，称为频谱域方法。图的频域卷积是在傅里叶空间完成的，我们对图的拉普拉斯矩阵进行特征值分解。

空间域方法：空间域方法作用与节点的邻居节点，使用周围K个邻居节点计算当前节点属性，根据迭代次数L可以取到周边L距离的节点属性。如GraphSAGE。

我们提出了一个通用框架，称为GraphSAGE(SAmple and aggreGatE)，用于归纳节点嵌入。与基于矩阵分解的嵌入方法不同，我们利用节点特征来学习一个可推广到看不见节点的嵌入函数。通过在学习算法中加入节点特征，我们可以同时学习邻居节点的拓扑结构以及节点特征在邻居节点中的分布。我们的算法也适用于没有节点特征的图。

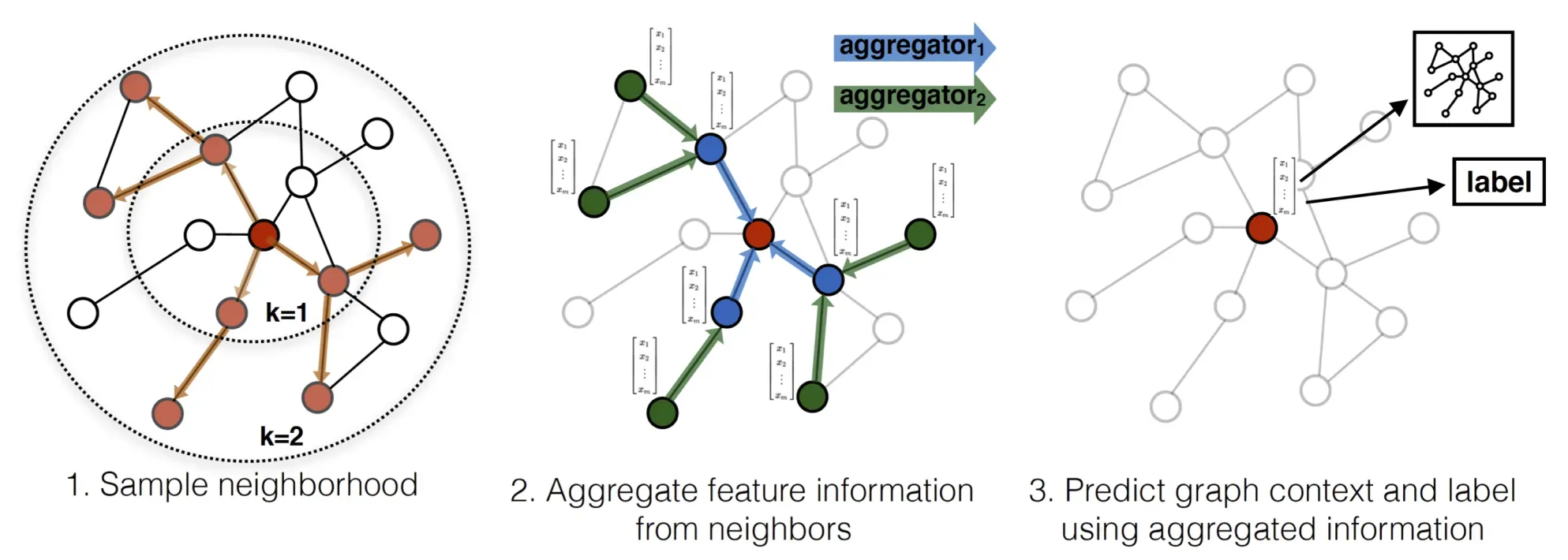
我们不是为每个节点训练一个不同的嵌入向量，而是训练一组聚合器函数，学习从节点的局部邻域聚合特征信息，如图1所示。每个聚合器函数从给定节点之外的不同跳数或搜索深度聚合信息。在test或inference时，我们使用经过训练的模型，通过应用学习的聚合函数，为新的节点生成嵌入。根据之前关于生成节点嵌入的工作，我们设计了一个无监督损失函数，该函数允许图在没有特定任务监督的情况下进行训练。我们还表明，图形图像可以在完全监督的方式下进行训练。

2. GraphSAGE方法

该方法的关键思想是学习如何从节点的局部邻域聚合特征信息

3.1 嵌入生成（前向传播）方法

这一节，我们描述了嵌入生成，或称为前向传播方法，即图网络已经训练好的情况下。特别地，假设已经学习了聚合K个邻居节点的函数的参数，表示为 NIPS17 GNN GraphSAGE 论文解读。它聚集了节点邻居的信息，以及一组权重矩阵，用于在模型的不同层或“搜索深度”之间传播信息。

算法步骤：

进入：

图
图节点特征
深度
权重矩阵
非线性激活函数
可微聚合函数，一般，
节点v的邻居节点

输出：

图节点向量表示

算法：
NIPS17 GNN GraphSAGE 论文解读
k为网络深度，也可理解为迭代次数、捕获邻居节点的跳数。训练中发现，迭代次数为2时最好。可以这么理解，k为跳数，当k只有1时，当前节点A只聚合了周围邻居节点B的信息，周围邻居节点B聚合了自身周围节点C的信息；当k为2时，代表在此一次迭代基础上，再迭代了一次，即当前节点吸收了已吸收C信息的邻居节点B的信息，获得了更远的节点的信息。如果迭代次数足够多，每个节点都可以获取全图的节点信息，这种获取信息的感觉和感受野类似，随着网络加深，或迭代次数加深，每个特征点能捕获到周围更多的信息。