1、什么是联合概率分布?
双向频率表是显示两个分类变量的频率(或“计数”)的表。
例如,下面的双向表显示了一项调查的结果,该调查询问了 100 人他们最喜欢哪种运动:棒球、篮球或足球。
行显示受访者的性别,列显示他们选择的运动:
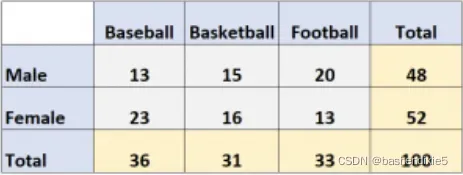
在此示例中,有两个变量:Sports 和 Gender。
联合概率分布简单地描述了给定个体为一个变量取两个特定值的概率。联合概率分布的要点是找到两个变量之间的关系。
“联合”这个词来自于我们对两件事同时发生的概率感兴趣的事实。
例如,在这 100 个人中,有 13 个人是男性,他们选择棒球作为他们最喜欢的运动。
因此,我们可以说给定个人是男性并选择棒球作为他们最喜欢的运动的联合概率是 13/100 = 0.13 或 13% 。
用数学符号写成:
P(性别=男性,运动=棒球)= 13/100 = 0.13 。
我们可以使用这个过程来计算整个联合概率分布:
- P(性别=男性,运动=棒球)= 13/100 = 0.13
- P(性别=男性,运动=篮球)= 15/100 = 0.15
- P(性别=男性,运动=足球)= 20/100 = 0.20
- P(性别=女性,运动=棒球)= 23/100 = 0.23
- P(性别=女性,运动=篮球)= 16/100 = 0.16
- P(性别=女性,运动=足球)= 13/100 = 0.13
请注意,概率之和等于 1 或 100% 。
2、为什么使用联合概率分布?
联合概率分布很有用,因为我们经常收集关于两个变量的数据,例如运动和性别,并且我们有兴趣回答与这两个变量相关的问题。
例如,我们可能想知道人口中某个特定个体是男性并且更喜欢棒球作为他们最喜欢的运动的可能性有多大。
或者我们可能想知道某个特定的人是女性并且喜欢足球作为他们最喜欢的运动的可能性有多大。
联合概率分布可以帮助我们回答这些问题。
使用以下示例作为练习,以更好地理解联合概率分布。
示例 1
以下双向表显示了一项调查的结果,该调查询问了 238 人他们最喜欢哪种电影类型:
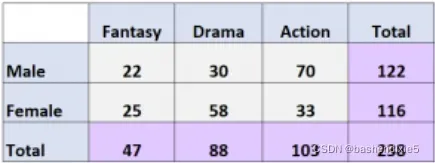
问题:给定的个体是女性并且更喜欢戏剧作为他们最喜欢的电影类型的概率是多少?
答案:P(性别 = 女性,类型 = 戏剧)= 58/238 = 0.244 = 24.4%
示例 2
下面的双向表显示了一个班级中 64 名学生的考试成绩,根据他们花费了多少小时来计算:
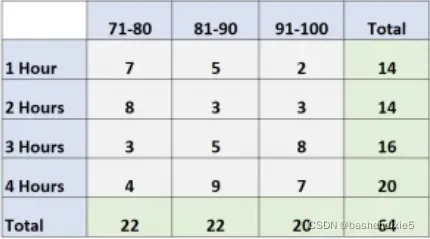
问题:给定个人学习 2 小时并获得 91 到 100 分的概率是多少?
答案:P(学习 = 2 小时,分数 = 91-100)= 3/64 = 0.047 = 4.7%
3、联合概率分布和监督学习
监督学习假设输入与输出的随机变量X和Y遵循联合概率分布P(X,Y)。P(X,Y)表示分布函数,或分布密度函数。注意在学习过程中,假定这一联合概率分布存在,但对学习系统来说,联合概率分布的具体定义是未知的。训练数据与测试数据被看作是依联合概率分布P(X,Y)独立同分布产生的。统计学习假设数据存在一定的统计规律,X和Y具有联合概率分布就是监督学习关于数据的基本假设。
文章出处登录后可见!
