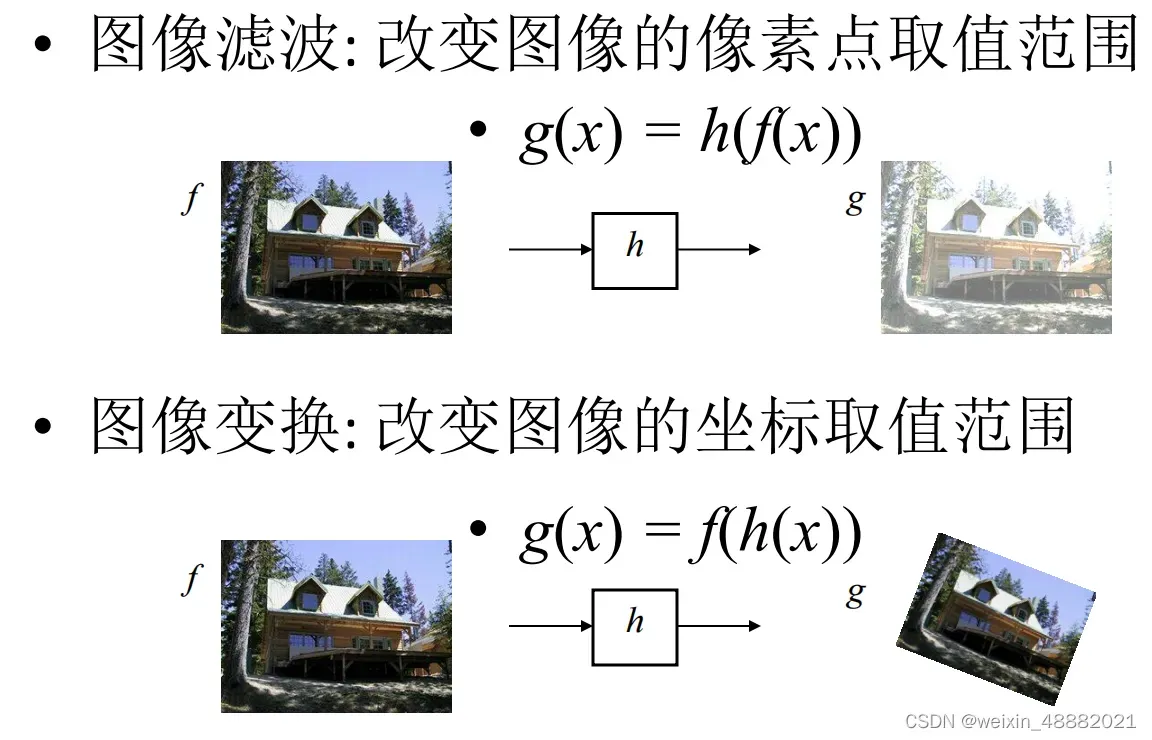
内容

1. 图像映射和全景拼接

1.1 简介

1.2 基础流程

1.3 计算图像之间的变换结构

1.4 图像拼接的几何原理

1.5 变换类型选择

1.6 2D 图像变换原理

1.7 变换参数求解

1.8 图像映射流程

1.9 图像拼接整体流程

2.全景拼接测试

2.1 代码展示

2.2 运行结果

1. 图像映射和全景拼接

1.1 简介

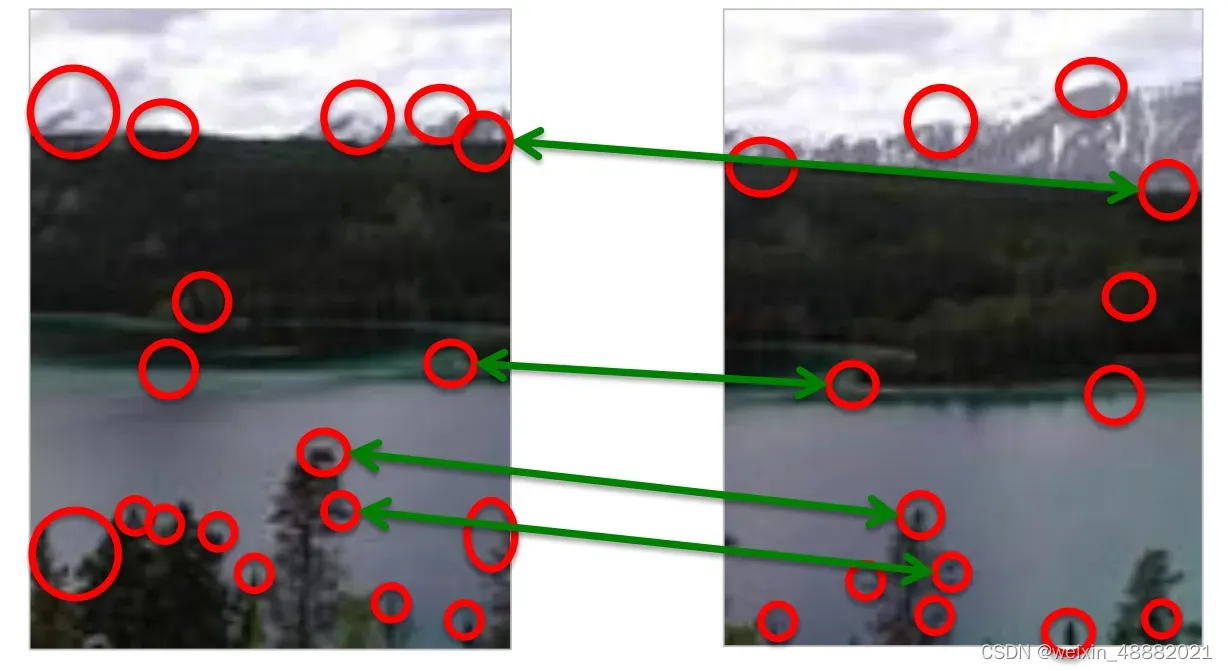
首先是在连续图像对间使用SIFT特征寻找匹配对应点对，SIFT是具有较强稳健性的描述子，能够比其他描述子产生更少的错误点，但是该方法仍不是很完美；使用RANSAC算法估计出图像间的单应性矩阵，判定哪些点对是正确的，哪些点对是错误的，即使用一个阈值来决定哪些单应性矩阵是合理的；然后将所有的图像扭曲到一个公共的图像平面上。

通常，这里的公共平面为中心图像平面。一种方法是创建一个很大的图像，比如将图像中全部填充0，使其和中心图像平行，然后将所有的图像扭曲到上面。由于我们所有的图像是由照相机水平旋转拍摄的，因此我们可以使用一个较简单的步骤：将中心图像左边或者右边的区域填充为0，以便为扭曲的图像腾出空间。
图像拼接的几何原理：全景融合的 3D 几何解释，图像被投影到共同的拼接平面上（同一坐标系）， 在拼接平面上实现全景融合。在拼接的应用中，其实可以简化理解为 2D图像的变换，叠加过程。

1.2 基础流程

① 拍摄场景的多张/连续图像

②计算第二张图像与第一张图像的变换关系

③ 将第二张图片叠加到第一张图片的坐标系中

④转化融合/合成

⑤ 在多画面场景下，重复上述过程

1.3 计算图像之间的变换结构

• 提取特征点

• 生成描述符

• 特征匹配

• 计算转换结构

1.4 图像拼接的几何原理

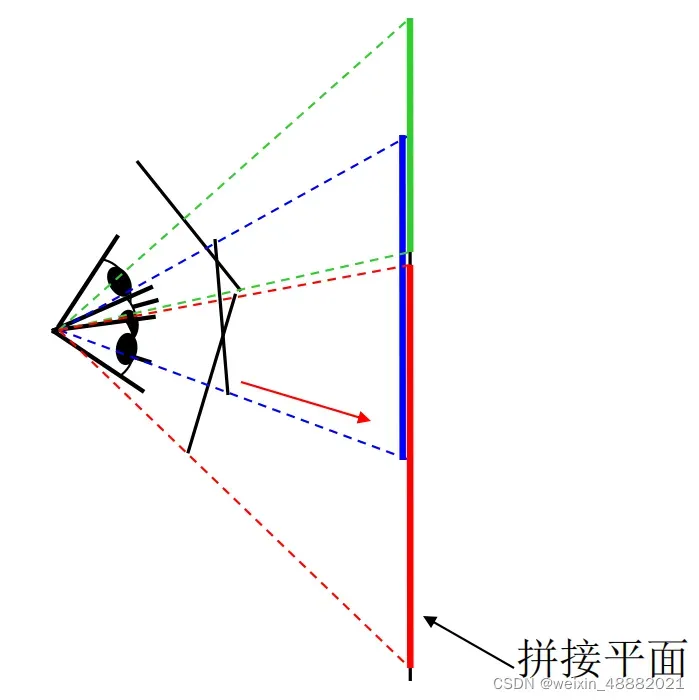
• 全景融合的 3D 几何解释

– 图像被投影到一个共同的拼接平面上（相同的坐标系）

– 拼接平面上的全景融合

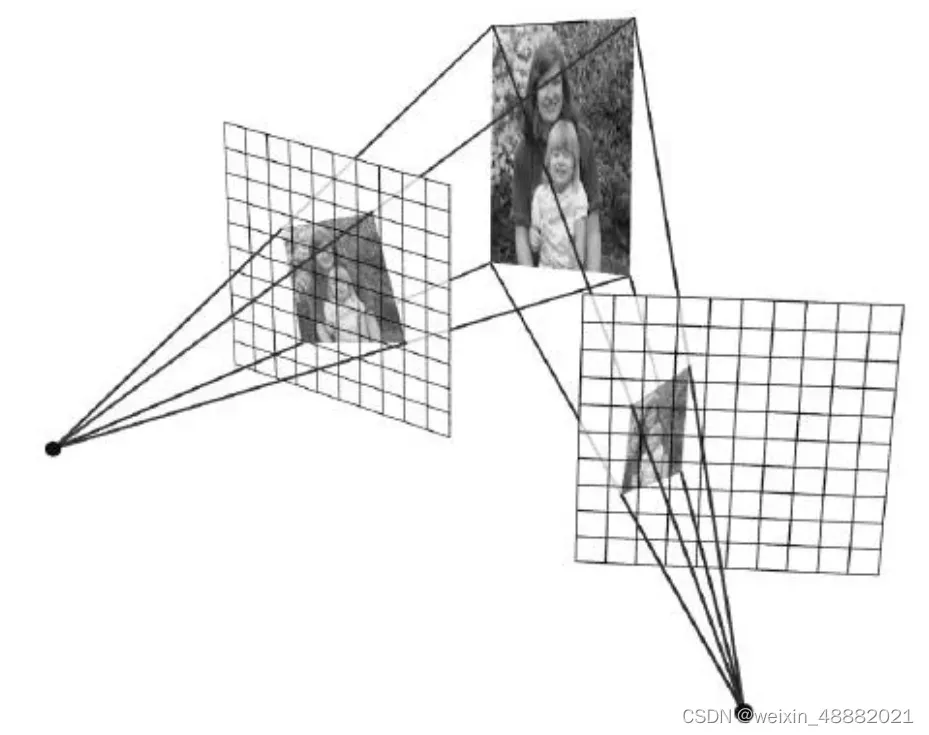
• 在拼接的应用中，其实可以简化理解为 2D 图像的变换、叠加过程

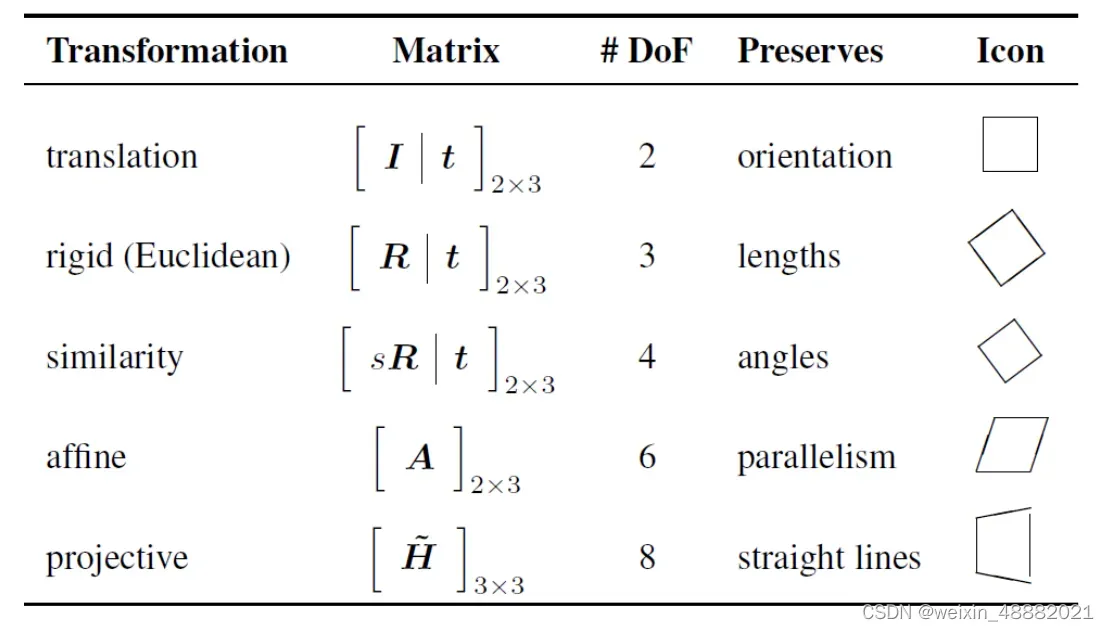
1.5 变换类型选择

• 要将两个图像叠加在一起，需要什么模型？

•translation （位移）

•rotation （旋转）

•scale （尺度 / 大小）

•affine （仿射）

• Perspective （透视）

1.6 2D图像变换原理

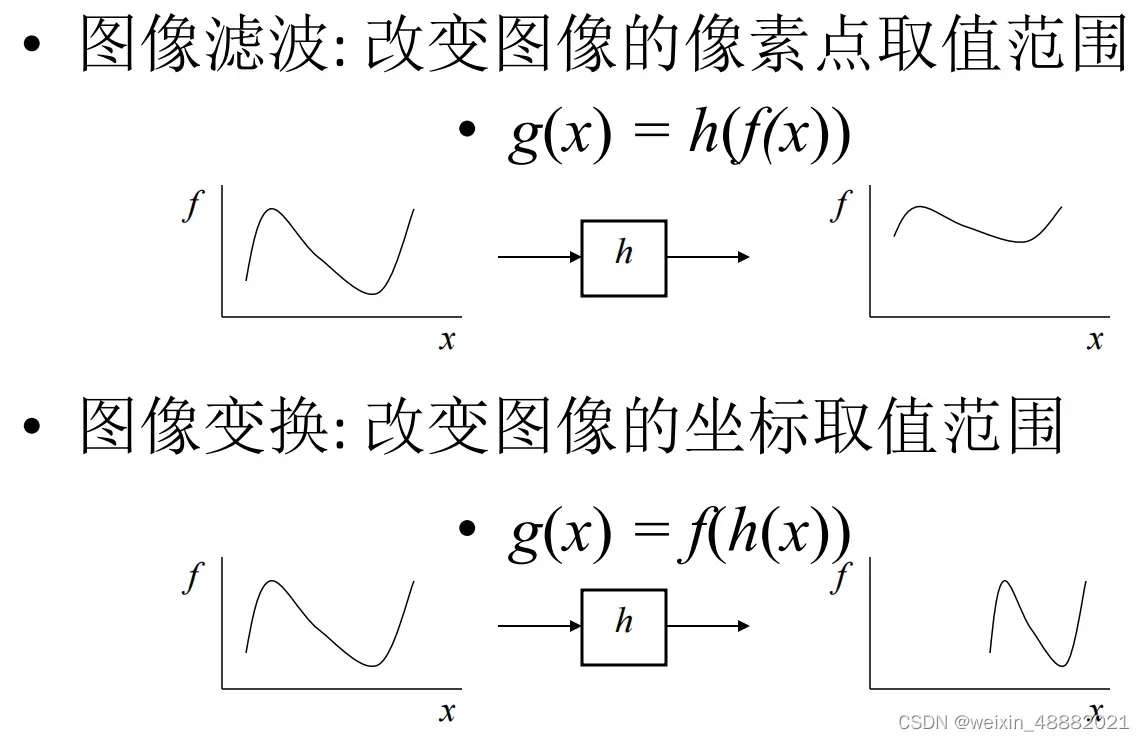
1.7变换参数求解

对于不同的问题，需要多少对匹配的特征来计算模型参数。

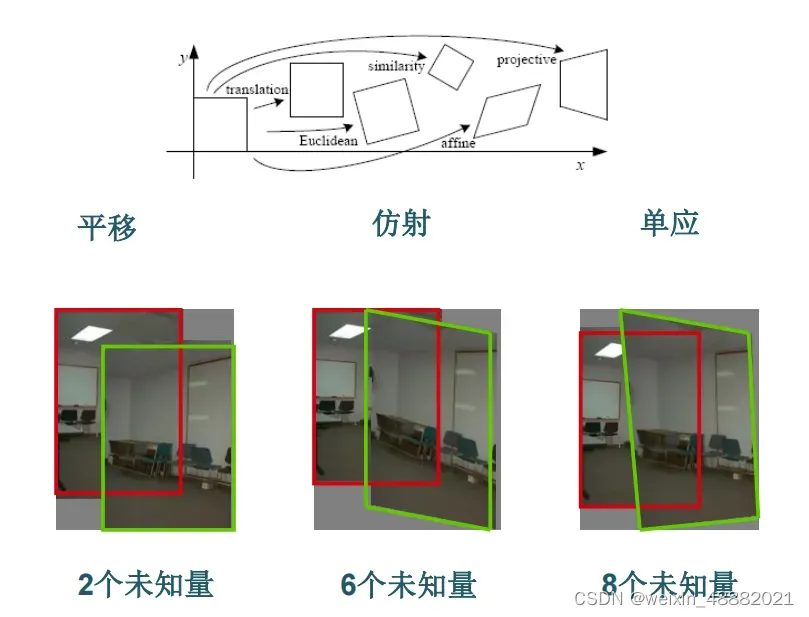
对于平移变换，有两个未知参数，需要一对点来列出要求解的两个方程。

1.8图像映射流程

① 两幅/多幅图像的特征提取

②特征匹配

③根据图像变换的特点，选择合适的变换结构

④根据 DLT 等方法计算变换结构

⑤使用正向/反向映射，并使用插值实现图像映射变换

1.9 图像拼接整体流程

• 基于给定图像/集的特征匹配

• 通过匹配特征计算图像之间的变换结构

•使用图像变换结构实现图像映射

•针对叠加后的图像，采用 APAP 之类的算法，对齐 特征点

•通过图形切割方法自动选择接缝

• 根据 multi-band blending 策略实现融合

2.全景拼接测试

2.1 代码展示

import matplotlib.pyplot as plt
from numpy import *
from PIL import Image

from PCV.geometry import homography, warp
from PCV.localdescriptors import sift
from PCV.tools import reviseSize

# 批量修改图像尺寸
path = "H:\\zhifangtu\\"
reviseSize.startAction(path,2000,1800)  # 设置图像的宽、高

# 设置数据文件夹的路径
featname = [path + str(i + 1) + '.sift' for i in range(5)]
imname = [path + str(i + 1) + '.jpg' for i in range(5)]

# 提取特征并匹配使用sift算法
l = {}
d = {}
for i in range(5):
    sift.process_image(imname[i], featname[i])
    l[i], d[i] = sift.read_features_from_file(featname[i])

matches = {}
for i in range(4):
    matches[i] = sift.match(d[i + 1], d[i])

# 可视化匹配
for i in range(4):
    im1 = array(Image.open(imname[i]))
    im2 = array(Image.open(imname[i + 1]))
    plt.figure()
    sift.plot_matches(im2, im1, l[i + 1], l[i], matches[i], show_below=True)


# 将匹配转换成齐次坐标点的函数
def convert_points(j):
    ndx = matches[j].nonzero()[0]
    fp = homography.make_homog(l[j + 1][ndx, :2].T)
    ndx2 = [int(matches[j][i]) for i in ndx]
    tp = homography.make_homog(l[j][ndx2, :2].T)

    # switch x and y - TODO this should move elsewhere
    fp = vstack([fp[1], fp[0], fp[2]])
    tp = vstack([tp[1], tp[0], tp[2]])
    return fp, tp


# 估计单应性矩阵
model = homography.RansacModel()

fp, tp = convert_points(1)
H_12 = homography.H_from_ransac(fp, tp, model)[0]  # im1 到im2 的单应性矩阵

fp, tp = convert_points(0)
H_01 = homography.H_from_ransac(fp, tp, model)[0]  # im0 到im1 的单应性矩阵

tp, fp = convert_points(2)  # 注意：点是反序的
H_32 = homography.H_from_ransac(fp, tp, model)[0]  # im3 到im2 的单应性矩阵

tp, fp = convert_points(3)  # 注意：点是反序的
H_43 = homography.H_from_ransac(fp, tp, model)[0]  # im4 到im3 的单应性矩阵

# 扭曲图像
delta = 2000  # 用于填充和平移

im1 = array(Image.open(imname[1]), "uint8")
im2 = array(Image.open(imname[2]), "uint8")
im_12 = warp.panorama(H_12, im1, im2, delta, delta)

im1 = array(Image.open(imname[0]), "f")
im_02 = warp.panorama(dot(H_12, H_01), im1, im_12, delta, delta)

im1 = array(Image.open(imname[3]), "f")
im_32 = warp.panorama(H_32, im1, im_02, delta, delta)

im1 = array(Image.open(imname[4]), "f")
im_42 = warp.panorama(dot(H_32, H_43), im1, im_32, delta, 2 * delta)

plt.figure()
plt.imshow(array(im_42, "uint8"))
plt.axis('off')
plt.show()

2.2 运行结果