参考

1. LeeML-Notes
   

强烈建议阅读一篇英文博客，讲得非常全面清楚。它的相应的中文翻译博客 参考https://blog.csdn.net/google19890102/article/details/69942970

1. 基本概念

在回归问题的第三步中，需要解决如下优化问题：

• :lossfunction（损失函数）
  
• :parameters（参数）
  

这里的parameters是复数，即指代一堆参数，比如上篇说到的和。

我们需要找到一组参数，使损失函数尽可能小，这个问题可以通过梯度下降法解决：

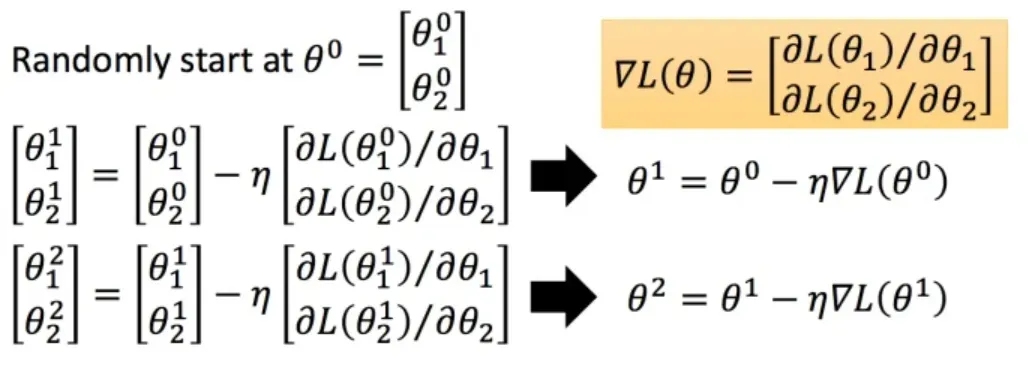
然后分别计算初始点处，两个参数对的偏微分，然后减掉乘上偏微分的值，得到一组新的参数。同理反复进行这样的计算。即为梯度，叫做Learning rates（学习速率）。

1.1 自适应学习率

采取一个简单的想法：随着次数的增加，将学习率降低一些因素

• 通常在开始时，初始点会远离最低点，所以使用较大的学习率
  
• update好几次参数之后比较靠近最低点了，此时减少学习率
  
• 例如，是次数。随着次数的增加，减少
  

学习率不可能是所有特征的值，不同的参数需要不同的学习率

1.2 Adagrad 算法

详情可参考知乎。Adagrad 涉及到动量的知识。

每个参数的学习率除以前一个导数的均方根。解释：

普通梯度下降是：

是参数

Adagrad 可以做的更好：

：前面参数所有导数的均方根，每个参数不同。

• 例子
  
  

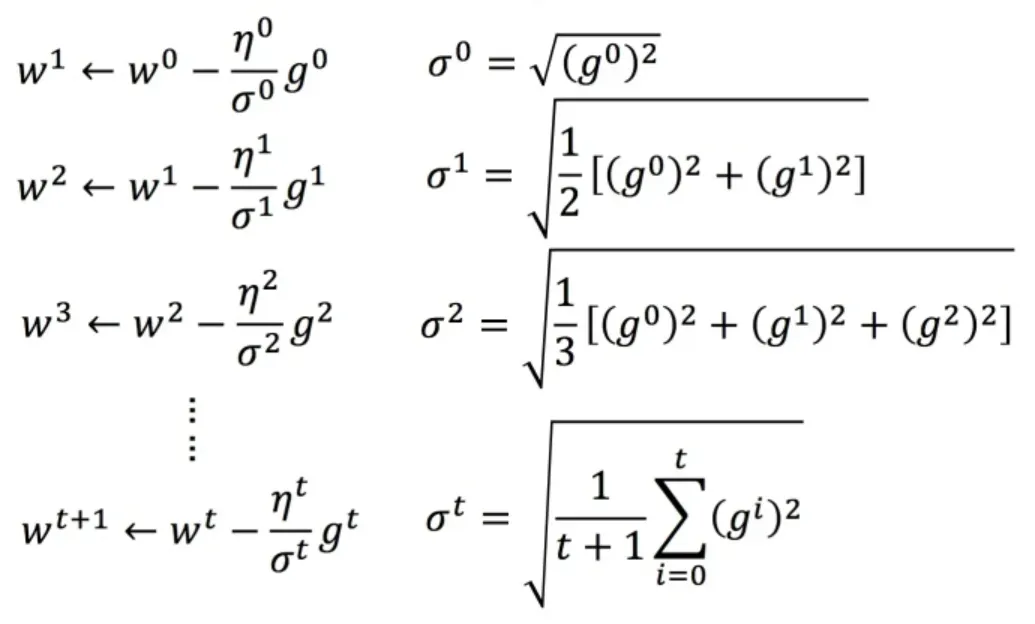
将 Adagrad 的式子进行化简：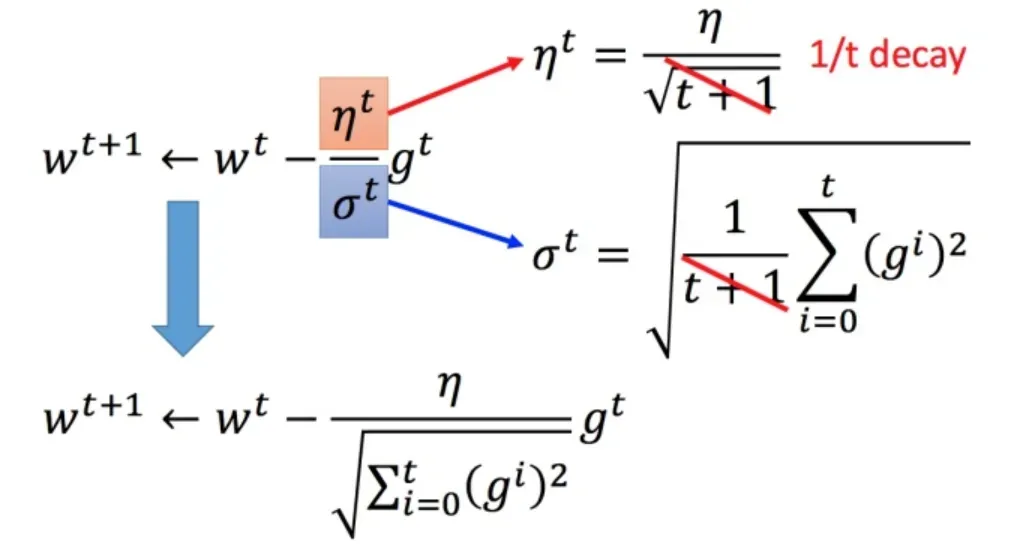

2. 随机梯度下降法

原始梯度下降公式为：

在随机梯度下降法中，损失函数不需要处理训练集中的所有数据，而是随机选择一个数据，如

此时不需要像之前那样对所有的数据进行处理，只需要计算某一个例子的损失函数Ln，就可以更新梯度。

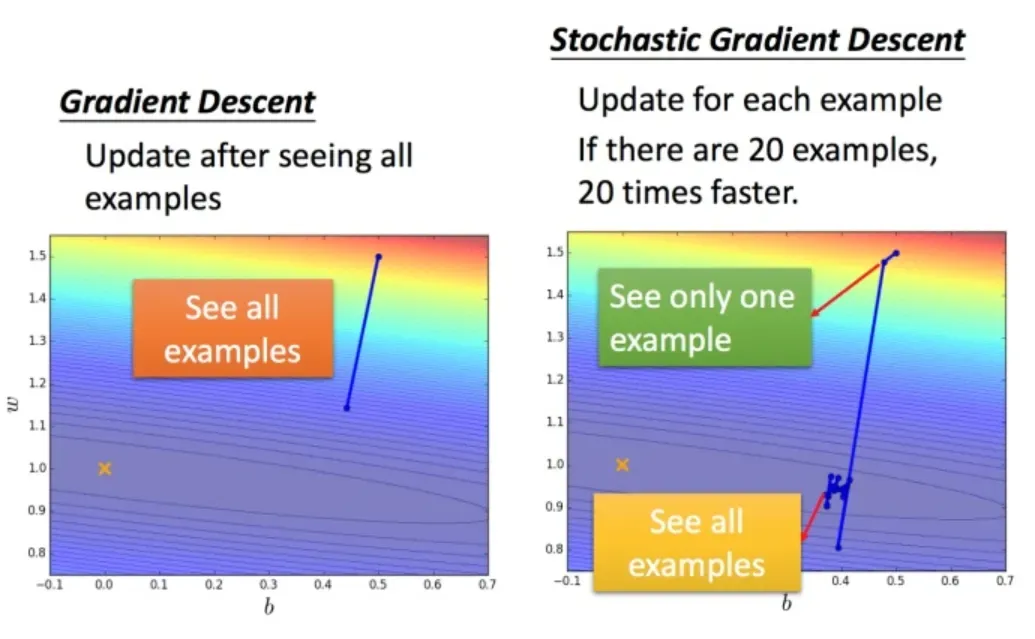
常规梯度下降法一步完成所有 20 个示例，但随机算法此时已经采取了 20 个步骤（针对每个处理的示例进行更新）

• 随机是指我们随机使用样本中的一个样本来逼近我所有的样本来调整θ，所以随机梯度下降会带来一定的问题，因为计算出来的梯度不是一个准确的，对于优化问题，凸问题，虽然损失函数每次迭代得到的不是全局最优解的方向，而是大整体的方向是全局最优解，最终的结果往往接近全局最优解
  
• 随机梯度下降法最终不会收敛到最优解，而是会收敛到最优解附近的一个浮动。
  

3. 理论基础

在解决梯度下降问题时：

每次更新参数，都会得到一个新的，使得损失函数变小。这是：

上述结论正确吗？

结论是不正确的。

比如在处，你可以在一个小圆圈里找到损失函数小的，继续寻找。

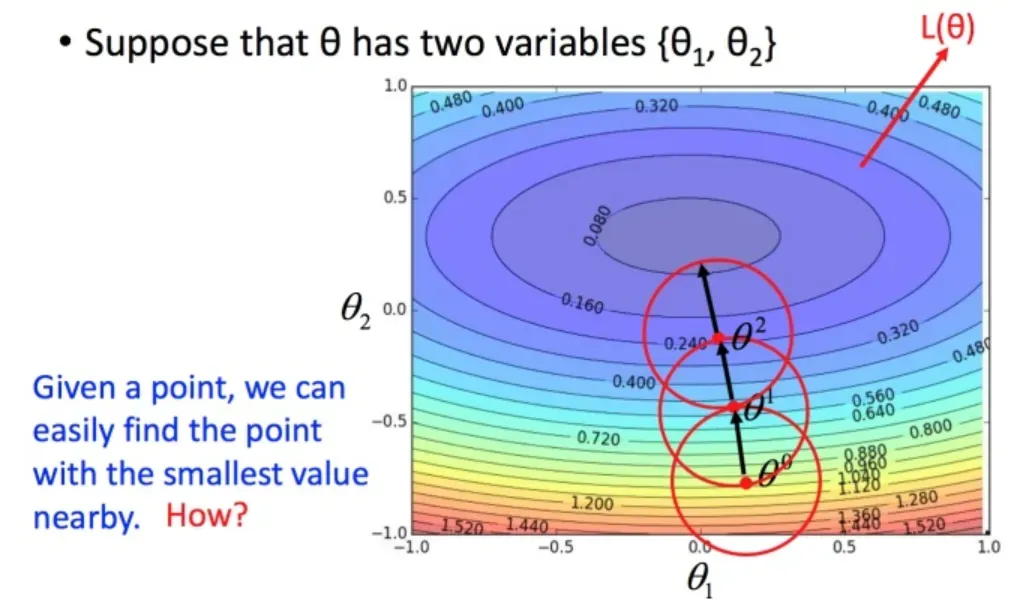
下一步是快速找到小圆圈中的最小值？

3.1 泰勒展开

定义

若在点的某个领域内有无限阶导数（即无限可微分，infinitely differentiable），那么在此领域内有：

当很接近时，有式14 就是函数在点附近关于的幂函数展开式，也叫泰勒展开式。

多元泰勒展开

以下是两个变量的泰勒展开式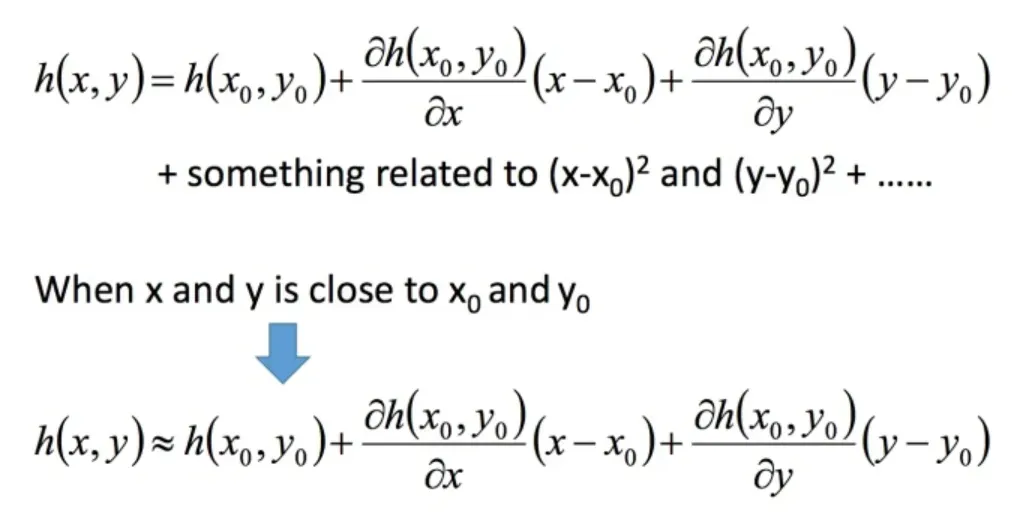

使用泰勒展开化简

回到如何快速找到圆内的最小值。基于泰勒展开式，在点红圈范围内，损失函数可以通过泰勒展开式简化：

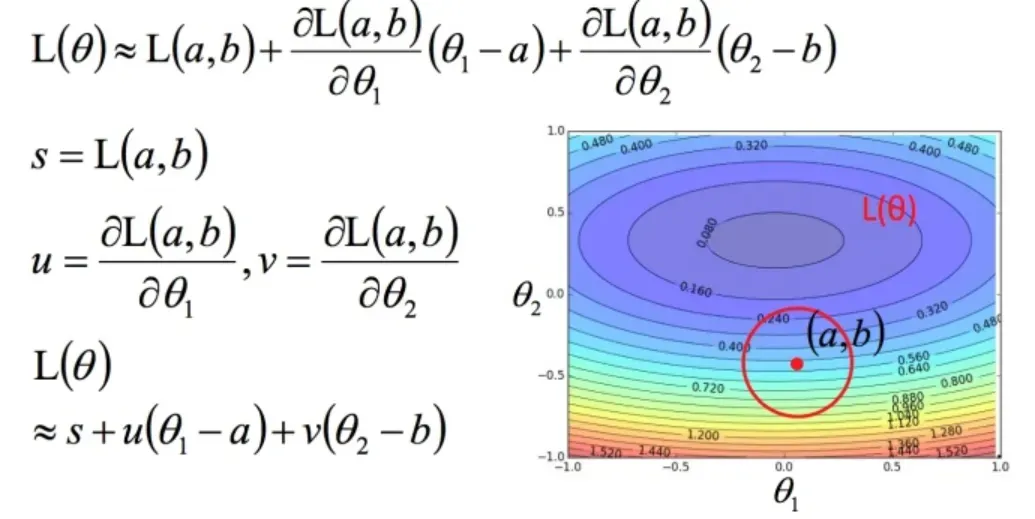
问题进一步简化为下图：

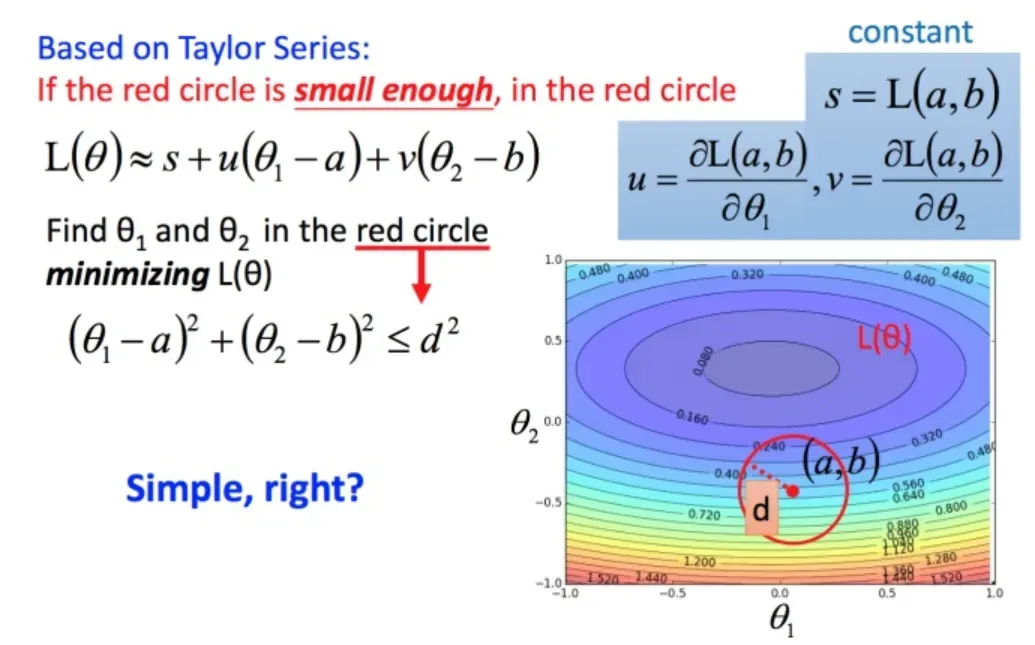
不考虑s的话，可以看出剩下的部分就是两个向量和的内积，那怎样让它最小，就是和向量方向相反的向量

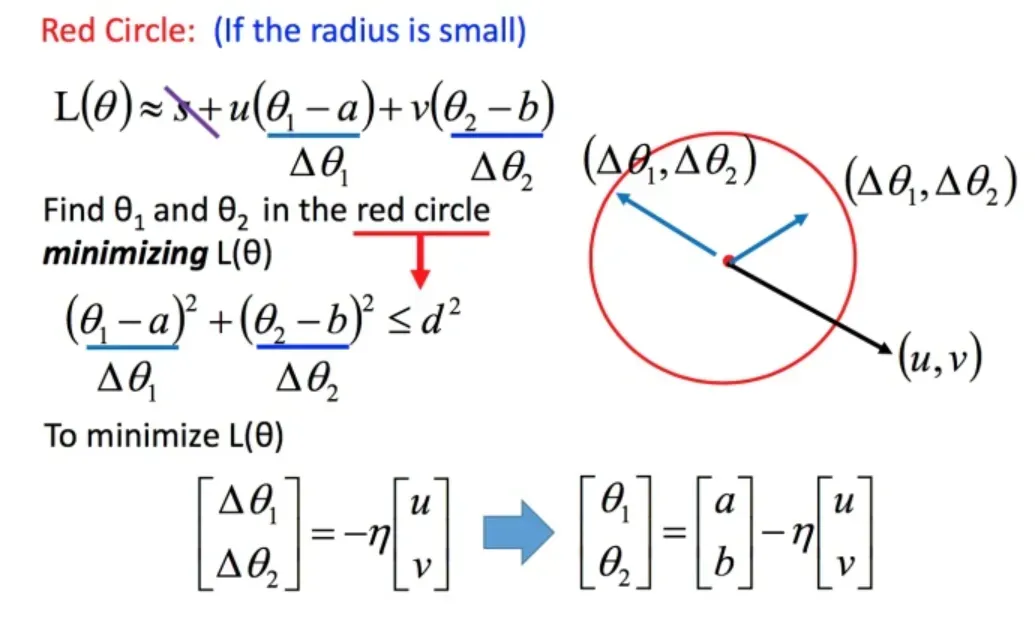
然后将u和v带入。

发现最后的式子就是梯度下降的式子。但这里用这种方法找到这个式子有个前提，泰勒展开式给的损失函数的估算值是要足够精确的，而这需要红色的圈圈足够小（也就是学习率足够小）来保证。所以理论上每次更新参数都想要损失函数减小的话，即保证式1-2 成立的话，就需要学习率足够足够小才可以。

所以实际中，当更新参数的时候，如果学习率没有设好，是有可能式1-2是不成立的，所以导致做梯度下降的时候，损失函数没有越来越小。

式1-2只考虑了泰勒展开式的一次项，如果考虑到二次项（比如牛顿法），在实际中不是特别好，会涉及到二次微分等，多很多的运算。

4. 梯度下降限制

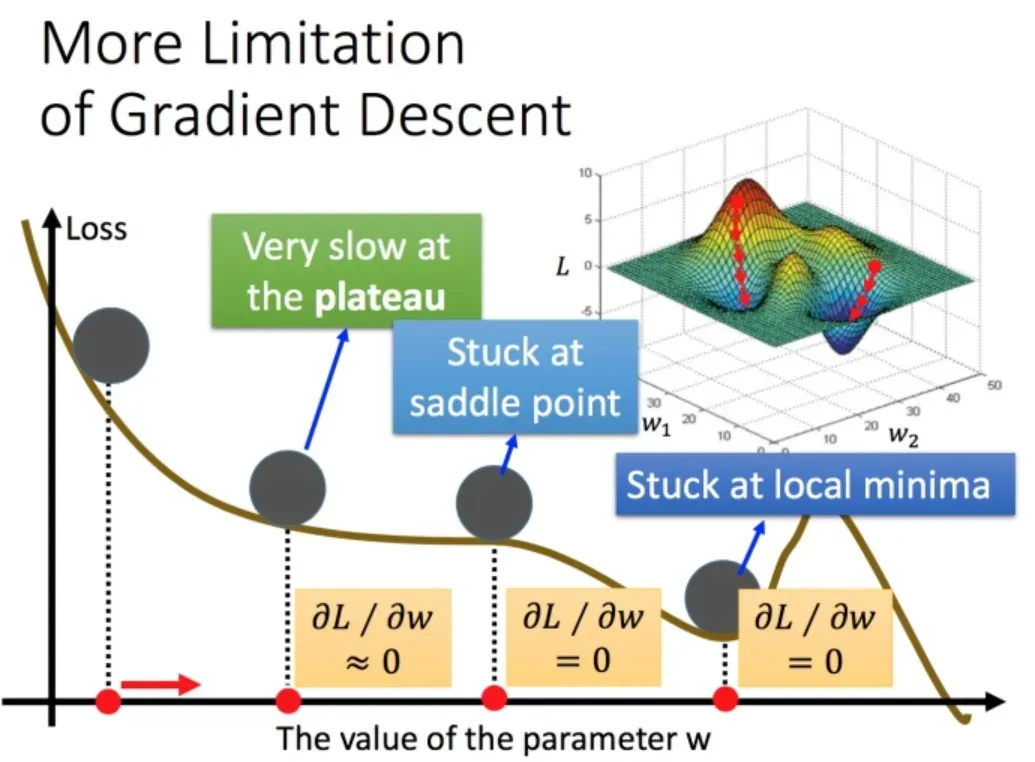
容易陷入局部极值 还有可能卡在不是极值，但微分值是0的地方 还有可能实际中只是当微分值小于某一个数值就停下来了，但这里只是比较平缓，并不是极值点。