走向深度关系学习[0]

使用 PyNeuraLogic 超越图神经网络

Python 中的可微分逻辑编程，用于优雅的编码和将 GNN 扩展到更复杂的深度关系模型

在之前的文章中，我们讨论了关系机器学习的问题，如何在关系逻辑中自然地表达它，以及为什么不能用标准的基于特征向量的模型（例如经典神经网络）来完全解决它。然后，我们回顾了旨在将逻辑与神经网络相结合的神经符号集成范式，简要回顾了其历史，并指出了主要挑战。最后，在上一篇文章中，我们讨论了如何用关系逻辑优雅地解决结构化深度学习模型（例如图神经网络 (GNN)）的最新进展。[0][1][2]

在本文中，我们将在一个名为 NeuraLogic 的实用框架中展示这些原则，旨在将深度学习与（可微分）逻辑编程相结合。我们将展示如何使用相应的 Python 库轻松实现现有 GNN 模型并将其扩展到更复杂和通用的功能，您将能够开始自己创建新颖的深度关系学习架构！

Data representation

让我们从如何表示数据开始。 NeuraLogic 中的数据样本以加权关系逻辑的表达格式存储（但为方便起见，在基本情况下也有来自常见张量格式的转换器）。正如前面文章中所讨论的，这是一种非常笼统的形式主义，涵盖了各种表示形式。由于我们将（再次）在这里使用众所周知的 GNN 作为示例，让我们更仔细地看一下相应图形数据格式的表示。[0]

简而言之，在关系逻辑中，我们定义了术语之间的关系，这些关系可以表示各种感兴趣的对象。然后，图只是节点之间二元边关系的集合。因此，给定一些节点 n1…nk，我们可以写成：

edge(n1,n3), edge(n2,n3), edge(n4,n5), …

请注意，此处的名称“edge”是任意的。我们可以为图的二元关系想出任何名称，例如

next(n1,n2), next(n2,n3), ... or   parent(n4,n1), parent(n4,n2), …

例如，表示图的一些特殊情况（序列和树）。我们还可以在同一个节点之间引入多个不同的关系：

related(n1,n3), neighbor(n1,n3), closeby(n1,n3), …

等等。请注意，节点（术语）的顺序表示（二元）关系是否对称，即这里的图是否是无向的。

• 这种对称性也可以隐式指定，例如有规律
  edge(Y,X) <= edge(X,Y) ，但稍后会详细介绍规则……

在 GNN 场景中，我们通常也将节点与一些属性或特征相关联。在分类属性的情况下，我们可以通过引入一元关系来保持清晰的逻辑领域，例如：

positive(n2), red(n1), …

对于数值特征，我们可以进一步将这些语句与（张量）值相关联，例如

[0.725, -1.6, …, 1.0] features(n2), ...

等等。¹同样，这里的“特征”名称是任意的，并且可以将多个不同的表示与每个节点相关联。

与许多 GNN 框架相比，将边缘与特征关联起来同样简单：

[1.2, -0.6,…] edge(n1,n3), ...

超越图形表示的偷窥

虽然我们可以用这种方式表示任意 GNN 数据，但 NeuraLogic 库中没有任何东西会限制您使用图形格式。因此，您可以疯狂地关联，例如，多个节点与“边”（超图）：

edge(n2,n3,n5,n4), ..., simplex(n2,n3,n4), complex(n1,n3,n5,n6)

或者创建全新的对象并将它们与新的关系和值相关联：

edge(n1,n2,e12), 0.9 covers(e12,n2), [0.8,1,…] in_graph(g1,e12), ...

and so on.

• 提示：数据表示基本上是一个关系数据库，每个表的每一行都有一个可选的（张量）权重。

然后，您可以将这些进一步组合成更复杂的表示（然后可用于促进更高级的推理过程，超越经典的基于边缘的消息传递方案）。

Model representation

用 NeuraLogic 语言表示模型与标准深度学习框架的区别甚至更大。与现有的程序方法相比，直接在计算图级别上使用张量表示进行操作，NeuraLogic 使用声明性逻辑编程来抽象模型的计算原理。

• 你肯定知道，例如 SQL，它也是一种声明性语言。

虽然这对于经典的张量运算深度学习问题可能显得有些多余，但在关系学习环境中它变得非常优雅，表现出各种形式的对称性。在这种情况下，使用 NeuraLogic 会产生更加紧凑和优雅的学习程序，直接表达每个模型的本质（例如 GNN 中节点和边的局部置换不变性）。[0]

简而言之，使用的逻辑编程范式是一种声明性编码方法，您可以在其中声明逻辑变量之间的关系，对应于域的对象（用大写字母书写以区别于术语）。例如，我们可以写

edge(X,Y)

描述图中任意一对节点（X 和 Y）之间所有边的集合。然后可以将这些进一步组合成模式，例如

edge(X,Y), edge(Y,Z), edge(Z,X)

在这样的图中表示一个三角形（3-cycle）。最后，这些模式可用于形成驱动计算（推理）的所谓“规则”。例如，我们可以写

in_triangle(X) <= edge(X,Y), edge(Y,Z), edge(Z,X).

为出现在三角形中的每个节点派生（推断）一个新属性“in_triangle”。

一组这样的规则然后形成一个所谓的逻辑程序，其执行相当于对规则进行逻辑推理。然后，NeuraLogic 框架使这个推理过程可区分，这反过来又使它等同于深度（关系）学习中的前向传播。最后，这些程序可以通过将（可学习的）权重与规则相关联来参数化，例如[0]

W₀ in_triangle(X) <= W₁ edge(X,Y), W₂ edge(Y,Z), W₃ edge(Z,X).

• 然后可以直接使用这样的规则来形成，例如，各种 subgraph/graphlet/motif/cellular GNN 等模型

如果您不熟悉该领域，这可能听起来有点过于抽象，但让我们继续上一篇文章中的基本 GNN 演练示例，以保持基础。[0]

在 NeuraLogic 中编码 GNN

从上一篇文章中，我们知道任何 GNN 模型的核心都有一个所谓的传播规则，用于在相邻节点之间传递和聚合“消息”。特别是，节点 X 的一些新表示（’new_message’）是通过聚合相邻节点 Y 的先前表示（’old_message’）来计算的，即在 X 和 Y 之间具有“边缘”的那些。写得更“正式”一点：[0]

new_message(X) <= old_message(Y), edge(X,Y).

在 NeuraLogic 中，这就是实际代码！它简单地读作：“要计算任何对象 X 的‘new_message’属性值，请取一些其他对象 Y 的‘old_message’属性值，其中两者之间存在关系‘边’。”²

然后，这个简单的语句编码了经典 GNN 的计算原理。最后，为了实际学习节点的一些有用（分布式）表示，我们只需将可学习的参数（矩阵 W）附加到此计算中，例如作为

W2 new_message(X) <= W1 old_message(Y) , edge(X,Y).

然后，底层计算将在（邻域）聚合之前通过可学习的 W1 矩阵投影您的输入节点嵌入（“old_message”），然后在聚合之后通过 W2 矩阵进行投影。假设您在 NeuraLogic (tanh+avg) 中保留默认激活/聚合函数设置，则此加权规则表示计算：

这是图卷积层（变体）的正式定义。

引擎盖下的偷窥

现在我们已经有了关系数据和编码的模型，我们可以开始在数据上训练模型。在这里，我们只需要确保输入数据表示与模型表示匹配，即对应关系命名相同。然后引擎将匹配表示并通过规则开始数据的推理，也就是前向传播。

在关系逻辑中，这个过程可能是相当复杂的，会自动引入很多中间概念。这正是我们利用简单优雅的程序对复杂的深度关系学习架构进行建模的优势。[0]

让我们再次访问 GCN 以更详细地揭示底层过程。假设我们用分子数据学习，这是一个突出的 GNN 应用领域。当然，通过指定包含的原子“a”（例如，a(o1)、a(h1)、…）和它们之间的键“b”（b(o1,h1)，分子图可以很容易地用逻辑表示），……）。接下来，我们定义 GCN 模型规则，就像上面一样，但使用分子中使用的原子 (‘a’) 和键 (‘b’) 的特定命名：

Wh₁ h(X) <= Wa a(Y), Wb b(X,Y).

其中“h”是原子的新诱导（“隐藏”）表示（下一个“层”）。然后，我们通常希望根据 w.r.t 对分子进行分类。一些目标，为此我们从原子表示中为图级“读数”引入另一个全局表示“q”（“查询”）：

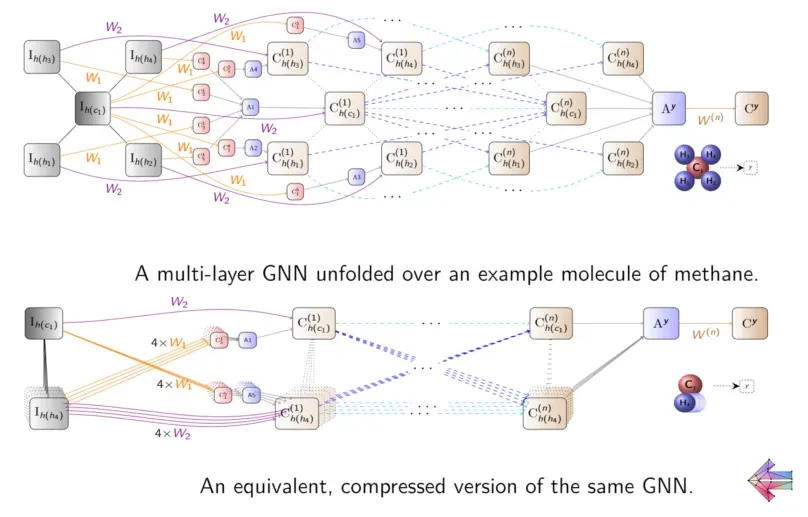
Wq q <= Wh2 h(X).

最后，通过 NeuraLogic 引擎运行这个关系规则集将得出一个反映逻辑推理过程的可微计算图，同时相当于 GCN 操作：

在此过程中，输入结构直接映射到“事实节点”，形成“规则节点”的输入。这些是通过逻辑变量的所有有效替换从程序规则中实例化的，这由底层推理引擎处理。规则节点可以被模糊地认为是“卷积”操作的实例化，因为它们还导致（地面）模型中的权重共享。然后将这些规则节点聚合在“聚合节点”中以产生新的表示，表示为“原子节点”，对应于规则的“头”（每个规则的左侧）。然后，相同的原理递归地应用于以蓝色显示的下一个（“读出”）规则。

最后，我们让与规则相关的权重（W）被（自动）优化，以通过梯度下降以标准方式反映给定查询（q）的预期输出值（Aq）。

有关更多详细信息，请查看 Github 上的 NeuraLogic 库或阅读相关的 Beyond GNN 论文 [3]。如果您想在更广泛的（科学）背景下理解概述的原则，欢迎您查看这篇论文，以深入了解具有关系逻辑表示的深度学习主题。[0][1][2]

到目前为止介绍的编码适用于普通的 NeuraLogic 框架，其中输入数据和模型是从明文解析的。当然，在纯文本文件中开发模型并不是很流行，对于机器学习实验也不是很方便。[0]

考虑到这一点，现在让我们将这种声明式、可微分的逻辑编程范式嵌入到普通的 Python 中，并进入我们在深度学习中都习惯的便利环境。为此，我们将使用一些智能 Python 运算符重载，并且为了保持简洁，我们现在将通过“键入”这些对象来明确标记什么是逻辑关系以及什么是变量

Relation.message(Var.X)     or, in short:        R.message(V.X)

然后，我们可以直接在 Python 中将与上述相同的 GCN 规则编码为

R.new_msg(V.X)[5,10] <= (R.old_msg(V.Y)[10,20], R.edge(V.X,V.Y))

包括相应（矩阵）参数化的维数规范。如果您想更改默认的激活/聚合函数，您可以另外将此（和其他）信息附加到每个规则，例如作为

(... <= ...) | [Activation.RELU, Aggregation.AVG]

将其缩小到经典的 GCN 层。

然后，这允许直接将引入的、相​​当非正统的、深度关系学习范式的好处与 Python 语言和生态系统的熟悉和方便的特性相结合。使用 PyNeuraLogic，您现在可以以一种与现有深度学习框架非常相似的便捷方式开始快速开发新颖的深度关系模型。

图深度学习及其他

介绍的 GCN 演练示例现在可以轻松扩展到各种其他 GNN 模型和学习场景。例如，您可以直接开始的一个有趣的扩展是在规则中包含子图模式，也称为“graphlets”或“motifs”等，例如我们上面开始的 in_triangle 示例。这增加了 GNN 的表达能力（超出了 WL 测试），并且目前正在探索这种“子图 GNN”的几种变体（例如，简单 GNN）。 PyNeuraLogic 是一个非常适合编码这些修改和扩展的框架。[0][1]

• 事实上，已经在提升关系神经网络 [9] 中使用 NeuraLogic 探索了各种类似的“graphlet-NN”架构，包括这些 [10] 的自动结构学习。最近还有一些简短的演示，例如分子环，可以帮助您入门 [11]。[0][1]

然而，重要的是，PyNeuralogic 绝不限于 GNN 模型。⁴ 让我们回忆一下所使用的声明性关系逻辑形式主义的表现力给我们带来了什么。首先，使用关系逻辑，我们不必关心如何将关系数据转换为张量（例如，如何将图排列成邻接矩阵）。而且由于没有这种隐含的张量表示，我们现在可以直接使用精心制作的模型所假设的对称性，并专注于它们的表现力，这与几何深度学习的精神非常相似。[0][1]

例如，当我们编写消息（X）时，代表所有节点的各自表示，这里没有潜在的排序（例如进入向量）。因此，这种一元关系语句可以直接用于定义在元素集（“深度集”）上运行的各种排列不变的深度学习架构。进一步研究二元关系，例如我们的 edge(X,Y) ，再次没有潜在的邻接矩阵表示。因此，我们可以直接使用在图同构不变性假设下运行的架构，例如 GNN 中已证明的节点和边的局部排列。⁵

将这些边的组合扩展到关系模式（例如子图）然后工作完全相同，因此这些不需要特殊（预处理）处理。当我们进一步将递归引入规则时，可以包括以组合（分形）对称性运行的各种递归神经架构。

请注意，在 PyNeuraLogic 中，这些原则不仅仅是一些数学抽象，而是直接可操作的，因为这正是您对模型本身进行编码的方式！

最后，当你超越图，引入多个更高数量的关系，并将它们组合成更复杂的模式和层次规则时，新的深度关系学习模型等待你去探索。为了给你一些入门的想法，在 PyNeuraLogic 中，你可以直接玩：

• 多种关系和对象类型
• 嵌套图、超图、关系数据库
• soft pattern matching
• 替代表示传播方案
• 包含逻辑背景知识
• and more…

在框架中，所有这些想法都采用相同形式的简单小（可微）逻辑程序，由于它们的声明性，这些程序通常高度透明且易于理解。⁶

所有这些特性使 PyNeuraLogic 非常适合您探索图深度学习的一些前沿！[0]

从学习到推理

虽然我们以 GNN 和类似模型训练中对 PyNeuraLogic 的解释为起点，但使用的逻辑形式自然也允许处理一些通用的 AI 功能，超出 ML 的观点。自然，逻辑是 AI 中任何形式的推理背后的核心形式，它在 PyNeuraLogic 中的使用可以让你在学习和推理之间顺利转换，这对于通用 AI 系统来说是一种越来越重要的能力。[0][1]

特别是，迄今为止我们用于对神经模型进行编码的关系规则可能会采用更具“指导性”的形式，以将逻辑推理引导到更复杂的推理任务中。例如，让我们重温一下著名的 DeepMind 对伦敦地铁路径进行推理的演示。[0][1]

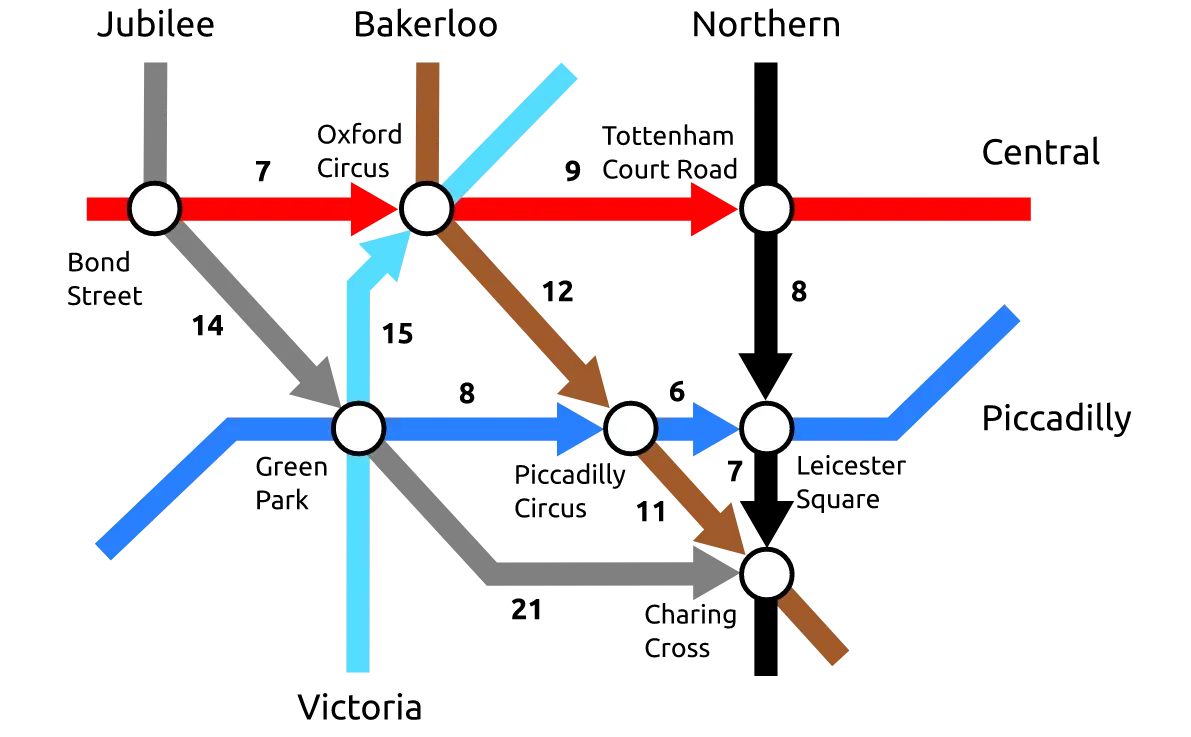
虽然这种形式的“算法推理”对于符号 AI 方法来说非常简单，但将其编码到神经模型（“可微神经计算机”）中需要 DeepMind 付出大量的努力和训练（由于“不适当的”、命题的、固定的大小张量学习表示）。

在 PyNeuraLogic 中，由于逻辑推理和神经推理之间的对偶性，解决此类问题非常简单。特别是，我们可以从采用符号方法开始，其中路径将是一个简单的递归定义，由两个规则组成，表示：

1. 如果两个站（X，Y）在数据中直接连接，则存在路径 X -> Y（递归的终止条件）：

R.path(V.X, V.Y) <= R.connected(V.X, V.Y)

2. 如果 X 连接到 Y 并且存在路径，则存在路径 X -> Z
Y->Z（递归定义）：

R.path(V.X, V.Z) <= ( R.connected(V.X, V.Y), R.path(V.Y, V.Z) )

运行逻辑推理，这是在将规则转换为计算图形时本地执行的，在一些（图形）数据上进行编码，例如作为：

R.connected(T.bond_street, T.oxford_circus),
R.connected(T.oxford_circus, T.tottenham_court_road),
...

然后将产生所有（且仅）查询的任何站点之间的有效路径。当然，这可以通过任何纯符号推理引擎轻松实现。然而，在 PyNeuraLogic 中，我们可以进一步为逻辑关系分配数值，例如表示地铁站之间的距离：

R.connected(T.bond_street, T.oxford_circus)[7]

并使用相同的推理引擎来产生例如最短路径（以 min 作为聚合函数）。最后，由于在 PyNeuraLogic 中，这种推理是可微分的，我们可以将可学习的权重附加到规则上，并在这些路径表示之上探索各种学习任务。⁷

• 您可以在 PyNeuraLogic 文档中更详细地探索这个“伦敦地铁”示例。[0]

Computing Performance

好的，所以这个新框架使用声明式编程通过关系逻辑中指定的底层对称性来编码（高级）神经模型，而不是在（命题）张量表示之上对代数运算进行通用编码。

现在，您可能认为这种疯狂的基于逻辑推理的 DL 方法至少会带来一些可怕的计算复杂性问题（通常与逻辑有关的任何事情都会出现这种情况，对吧？）。

毕竟，张量表示和并行处理的诱导可能性是深度学习计算成功的主要原因。然而，对于稀疏和不规则数据表示和计算图的关系问题，情况并非（必然）如此。在那里，“把一切都变成张量”的思维偏差实际上可能会使模型不仅可读性降低，而且效率也会降低！[0]

PyNeuraLogic 实例化了这些见解，在允许您轻松声明更具表现力的模型的同时，它也经常在经典 GNN 模型的游戏中击败标准框架的计算性能。

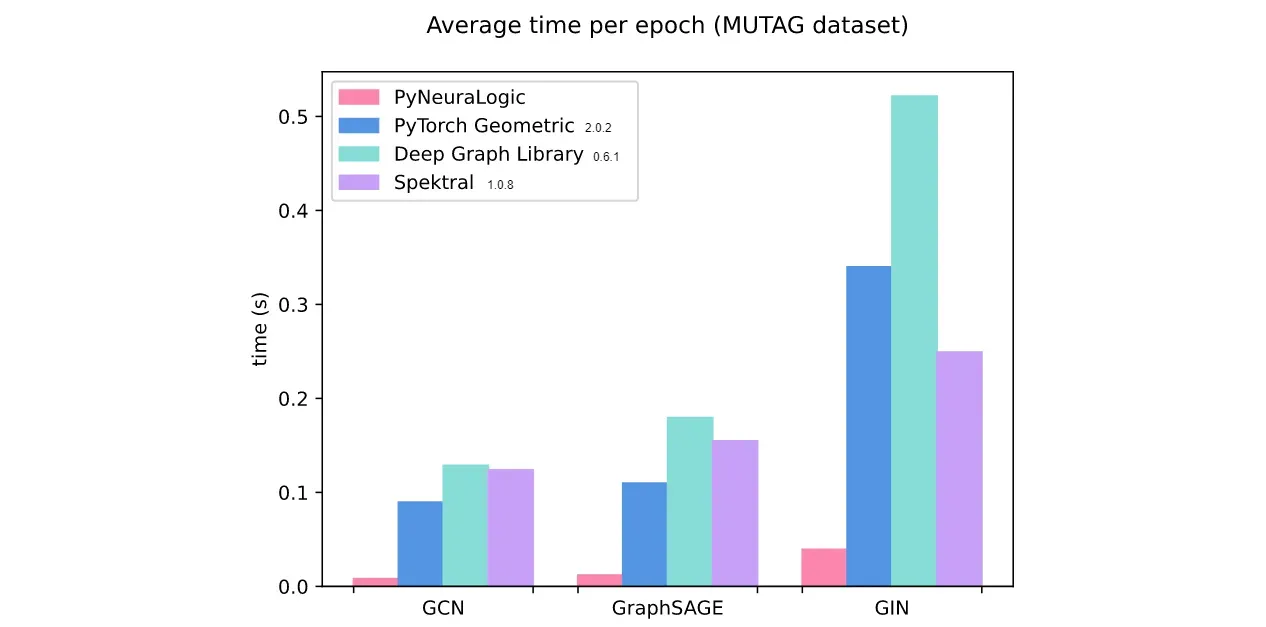
查看我们的基准测试，我们证明对于一系列常见的 GNN 模型和应用程序，例如使用分子学习，PyNeuraLogic 实际上比流行的 GNN 框架快得多。[0]

这（部分）也是由于符号 AI（“提升推理”）中已知的高级加速技术，由于 PyNeuraLogic 中使用的逻辑表示，它也可以应用于神经模型（如 ICLR 论文 [8 ]）。[0]

Conclusion

最后，我们引入了一个新的、相当非正统的 Python 深度关系学习框架，它将神经网络与关系逻辑相结合，以支持开发具有高级学习和推理能力的复杂神经架构。对于初学者来说，它可以有效地捕捉经典的 GNN 模型，但它本质上更具表现力。

我们诚挚邀请您试用 PyNeuraLogic[0]

$ pip install neuralogic

并开始探索您对新的深度关系模型的想法。还有一些示例在线笔记本可以帮助您入门。[0]

• 如果您有任何改进或合作的想法，请联系我们！

如果不出意外，我们希望至少为您提供关于 GNN 模型类的新视角，以及深度学习和符号 AI 范式如何很好地结合在一起……

1. 还要注意，对于如何将这些表示混合在一起没有句法限制，因此可以选择数据的哪些部分用（子符号）分布式数字表示更好地建模，哪些部分可以自己被表示通过纯粹的逻辑方式，并根据需要沿着这个维度不断移动。

2. 再次注意，这里的名称是完全任意的，唯一重要的是表达逻辑变量之间关系的有向关系模式，通过 GNN 中的 WL 捕捉局部邻域聚合的原理。

3. Sourek、Gustav、Filip Železný 和 Ondřej Kuželka。 “超越具有提升关系神经网络的图神经网络。”机器学习 110.7（2021）：1695–1738。

4. 这就是为什么不需要对图中的子图进行预处理并在顶部运行标准 GNN 的原因，就像在某些工作中所做的那样，但是整个消息传递方案可以调整为直接在子图上操作相反，正如最近的蜂窝 GNN 或前面提到的 NeuraLogic 的“分子环 GNN”[11] 演示所提出的那样。[0][1]

5. 请注意，同样的假设适用于流行的 Transformer 架构，我们只假设一个完全连接的图（这相当于不假设任何边，而是简单地聚合给定范围内的所有其他对象）。

6. 因此，您无需为底层（例如，GNN）计算的每个小修改设计一个黑盒类名称动物园，因为您在此处直接在逻辑原则级别进行编码。

7. 在这个简单的例子中，这基本上对应于在后台训练大量小型递归神经网络。

[8] Sourek、Gustav、Filip Zelezny 和 Ondrej Kuzelka。 “通过提升对结构化卷积模型进行无损压缩。” ICLR，2021 年。

[9] 苏雷克、古斯塔夫等人。 “提升的关系神经网络。” arXiv 预印本 arXiv:1508.05128 (2015)。

[10] 苏雷克、古斯塔夫等人。 “用于提升关系神经网络的堆叠结构学习。”归纳逻辑编程国际会议。施普林格，湛，2017。

[11] Sourek、Gustav、Filip Zelezny 和 Ondrej Kuzelka。 “学习图神经网络之外的分子。” arXiv 预印本 arXiv:2011.03488 (2020)。

作者非常感谢 Lukas Zahradnik 校对这些帖子并开发了 PyNeuraLogic。[0][1]