🌞欢迎来到机器学习的世界
🌈 博客主页:青云阁💌欢迎关注🎉点赞👍收藏⭐️评论📝
🌟本文由青云阁原创!
🌠此阶段属于练气阶段,希望你顺利完成突破
📆首发时间:🌹2021年5月5日🌹
✉️希望和你一起完成进阶之路!
🙏作者水平非常有限,如果发现错误请留言炸!非常感谢!

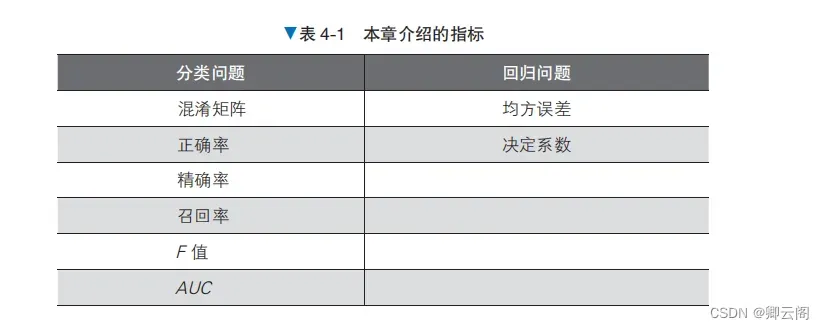
🍈 1. 监督学习的评价
🍉 2. 分类问题的评估方法[0]
这里把目标变量(类别标签数据)的 0 和 1 反转了。这是为了将恶性视为 1 (阳性),将良性视为 0(阴性)。在 scikit-learn 中,标签往往没有意义。这个数据本来是将恶性视为 0 的,但是在实际的诊疗中,一般将发现恶性肿瘤作为检查目标,所以就这个问题来说,把恶性当 作阳性来处理更加自然。from sklearn.datasets import load_breast_cancer data = load_breast_cancer() X = data.data y = 1 - data.target # 反转标签的0和1 X = X[:, :10] from sklearn.linear_model import LogisticRegression model_lor = LogisticRegression() model_lor.fit(X, y) y_pred = model_lor.predict(X)混淆矩阵首先要介绍的分类问题评估指标是混淆矩阵(confusion matrix)。混淆矩阵可以将分类结果以 表格的形式汇总,这样就可以检查哪些标签分类正确,哪些标签分类错误。我们可以通过 scikit learn 的 confusion_matrix 函数创建混淆矩阵。from sklearn.metrics import confusion_matrix cm = confusion_matrix(y, y_pred) print(cm) 结果: [[337 20] [ 30 182]]将这个二元分类的结果作为混淆矩阵输出,我们会得到一个 2 行 2 列的矩阵。它是一个真实数据(正确答案)和预测数据的矩阵。
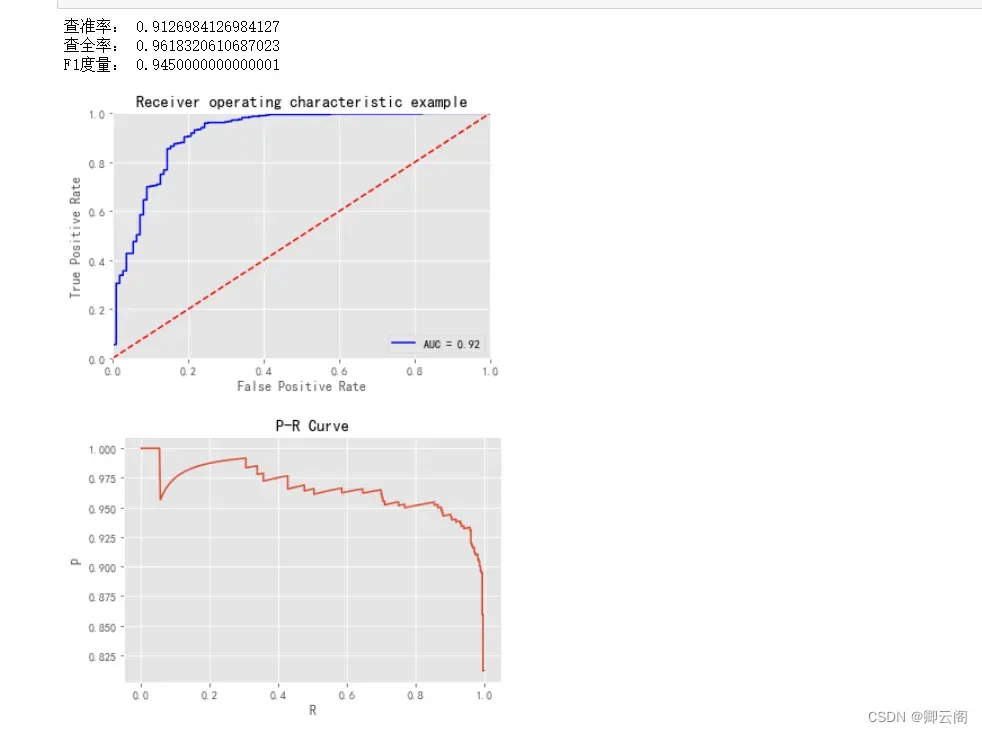
正确率正确率(accuracy)指的是预测正确的结果占总预测结果的比例。accuracy_score 函数用于计算正确率。from sklearn.metrics import accuracy_score accuracy_score(y, y_pred)0.9121265377855887这里输出的是基于“作为实际答案的目标变量 y”和“使用学习后的模型预测的 y_pred”计算出来的正确率。 正确率超过了 90%,看上去模型正确地学习了数据。精确率精确率(precision)指的是在所有被预测为阳性的数据中,被正确预测为阳性的数据所占的比 例。precision_score 函数用于计算精确率。from sklearn.metrics import precision_score precision_score(y, y_pred)0.900990099009901召回率召回率指的是在实际为阳性的数据中,被正确预测为阳性的数据所占的比例。recall_score函数用于计算召回率。from sklearn.metrics import recall_score recall_score(y, y_pred)0.8584905660377359F 值F 值是综合反映精确率和召回率两个趋势的指标。f1_score 函数用于计算 F 值。from sklearn.metrics import f1_score f1_score(y, y_pred)0.8792270531400966精确率和召回率之间是此消彼长的关系,如果试图让其中一个的值更高,则会导致另一个的值 更低。如果这两个指标同等重要,可以观察 F 值。ROC 曲线与AUC在输入数据有偏差的情况下,比如阳性数据有 95 个,阴性数据有 5 个的情况下, 正确率会高达 95%。 虽然这个模型是一个极端的例子,但是在实际工作中,这种没有经过很好训练的模型因数据不 均衡而计算出高正确率结果的情况经常出现。 应对数据不均衡问题的指标有 AUC(Area Under the Curve,曲线下面积)。AUC 指的是 ROC (Receiver Operating Characteristic,接收器操作特性)曲线下的面积。这里的 ROC 曲线指 的是横轴为假阳性率(即 FP 的占比),纵轴为真阳性率(即 TP 的占比)的图形。图中显示了当预 测数据为阳性的预测概率的阈值从 1 开始逐渐下降时,FP 和 TP 之间关系的变化。 假阳性率、真阳性率是可视化 ROC 曲线的必要条件,可以使用 roc_curve 函数计算。from sklearn.metrics import roc_curve probas = model_lor.predict_proba(X) fpr, tpr, thresholds = roc_curve(y, probas[:, 1]roc_curve 函数的输入是目标变量(类别标签数据)和预测概率。这里使用 predict_proba 方法计算了预测概率。下面在 Matplotlib 中对 roc_curve 函数输出的 fpr 和 tpr 进行可视化。%matplotlib inline import matplotlib.pyplot as plt plt.style.use('fivethirtyeight') fig, ax = plt.subplots() fig.set_size_inches(4.8, 5) ax.step(fpr, tpr, 'gray') ax.fill_between(fpr, tpr, 0, color='skyblue', alpha=0.8) ax.set_xlabel('False Positive Rate') ax.set_ylabel('True Positive Rate') ax.set_facecolor('xkcd:white') plt.show()ROC 曲线下方的面积是 AUC。面积的最大值是 1,最小值是 0。AUC 越接近于 1(面积越大), 说明精度越高;如果其值在 0.5 左右,则说明预测不够理想。换言之,如果值在 0.5 左右,则得到 的分类模型和抛硬币随机决定良性恶性没多大区别。roc_auc_score 函数用于计算 AUC 值。from sklearn.metrics import roc_auc_score roc_auc_score(y, probas[:, 1])AUC 的结果约为 0.977,接近于 1。对于一个分类模型来说,这样的精度是很高的。由于乳腺癌的数据偏差不大,所以用正确率来考查模型的性能也没有太大问题。不过如果输入 数据为关于“观看网站广告的用户中有多少会购买商品”的预测数据,那么正例和反例的数量可能 有相当大的偏差,常常出现正确率为 0.99,但 AUC 只有 0.6 的情况。在处理不均衡数据时,我们使 用 AUC 作为指标。from sklearn.preprocessing import StandardScaler import pandas as pd import matplotlib.pyplot as plt import numpy as np from sklearn.metrics import accuracy_score from sklearn.metrics import recall_score from sklearn.metrics import precision_recall_curve, roc_curve, auc from sklearn.metrics import f1_score dataset = pd.read_excel('d:\\huqidata.xlsx') data = dataset.iloc[:,1:-1] #从1列到最后一列为呼气数据的特征数据 label = dataset.iloc[:,-1] #最后一类为标签,1代表不吸烟,0代表吸烟 from sklearn.model_selection import train_test_split x_train,x_test,y_train,y_test = train_test_split(data,label,test_size=0.45,random_state=10) scaler = StandardScaler() scaler.fit(x_train) X_train = scaler.transform(x_train) X_test = scaler.transform(x_test) from sklearn.ensemble import GradientBoostingClassifier gbc = GradientBoostingClassifier() gbc.fit(X_train, y_train) y_pred = gbc.predict(X_test) #进行预测 print('查准率:',accuracy_score(y_test,y_pred)) print('查全率:',recall_score(y_test,y_pred)) print('F1度量:',f1_score(y_test,y_pred)) #画ROC曲线并计算AUC值 y_pred_gbc = gbc.predict_proba(X_test)[:,1] ###这个用于预测概率 fpr, tpr, threshold = roc_curve(y_test, y_pred_gbc) ###画图的时候要用预测的概率 roc_auc = auc(fpr, tpr) plt.plot(fpr, tpr, 'b', label='AUC = %0.2f' % roc_auc)#生成ROC曲线 plt.legend(loc='lower right') plt.plot([0, 1], [0, 1], 'r--') plt.xlim([0, 1]) plt.ylim([0, 1]) plt.xlabel('False Positive Rate') plt.ylabel('True Positive Rate') plt.title('Receiver operating characteristic example') plt.show() #画PR曲线 P,R, thresholds = precision_recall_curve(y_test, y_pred_gbc) plt.xlabel("R") plt.ylabel("P") plt.title('P-R Curve') plt.plot(R,P) plt.show()
🍅 3.回归问题的评价方法
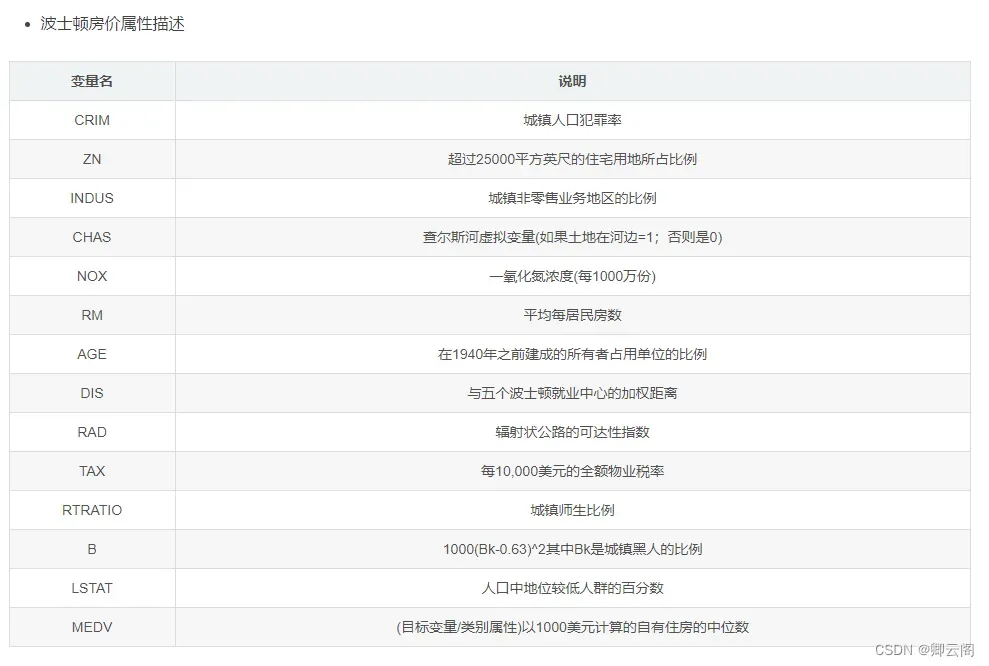
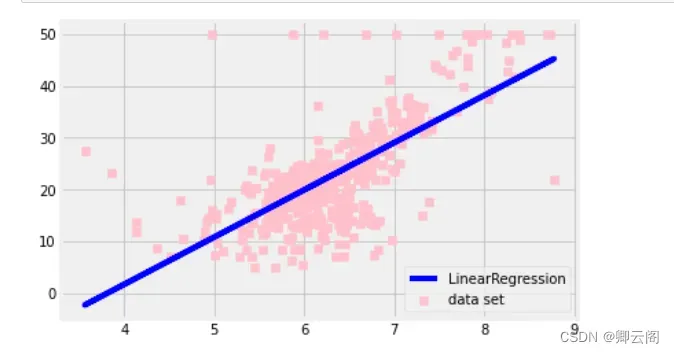
这里使用的数据是美国波士顿的房价数据集。这个数据集有 13 个特征变量,目标变量是 5.0 ~ 50.0 的数值。简单起见,这里介绍一元回归的评估方法,所以我 们只使用 13 个特征变量中的“住宅平均房间数”(列名为 RM)。设从数据集中的特征变量选择的平均房间数的列为 X,目标变量为 y。虽然特征变量 X 是由一列组成的数据,但这里也按照惯例使用大写的 X。目标变量 y 是数值数据。X 是 506 行 1 列的 数据,y 也是 506 行 1 列的数据。from sklearn.datasets import load_boston data = load_boston() X = data.data[:, [5,]] y = data.target上面的代码导入并使用了 LinearRegression 类,然后初始化 model_lir,使用 fit 方法进行训练。接着,代码使用训练好的 model_lir 的 predict 方法进行预测,并将预测结果赋给变量 y_pred。 本次使用的 LinearRegression 是一种线性回归算法。另外,由于特征变量是 1 列数据,所 以模型可以使用线性方程 y = ax + b 表示。现在看一下斜率 a 和截距 b 的值。from sklearn.linear_model import LinearRegression model_lir = LinearRegression() model_lir.fit(X, y) y_pred = model_lir.predict(X)print(model_lir.coef_) print(model_lir.intercept_)[9.10210898] -34.67062077643857斜率 a 约为 9.10,截距 b 约为 –34.67,所以本次训练的模型可以表示为直线 y =9.10x –34.67。 当房间数为 5 时,将其代入该式,有 9.10×5–34.67,可以得到预测租金为 10.83。线性回归利用训 练数据确定学习参数 a 和 b。随着训练数据的增减,这些学习参数会变为不同的值。 接下来绘制预测结果的图形,来看一下训练好的模型是如何预测的。由于这次是基于一个特征 变量(平均房间数)对目标变量(租金)进行预测的,所以我们可以绘制一个横轴为平均房间数, 纵轴为租金的图形。下面使用 Matplotlib 查看数据。%matplotlib inline import matplotlib.pyplot as plt fig, ax = plt.subplots() ax.scatter(X, y, color='pink', marker='s', label='data set') ax.plot(X, y_pred, color='blue', label='LinearRegression') ax.legend() plt.show()
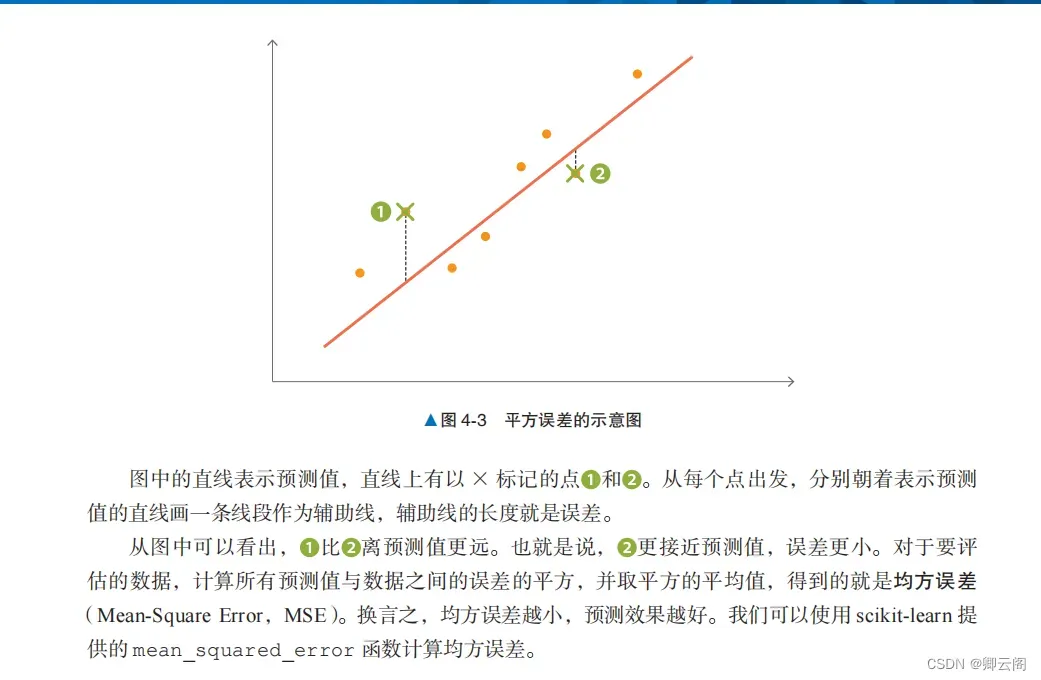
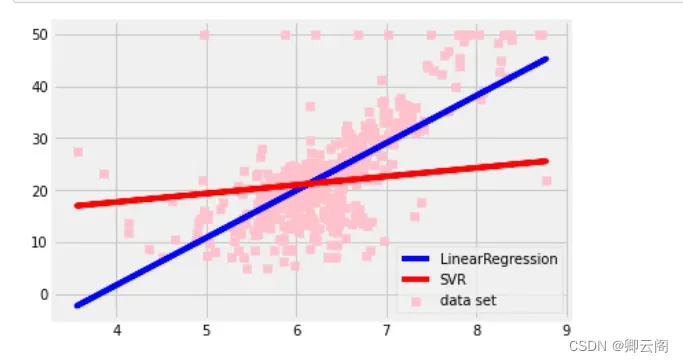
均方误差平方误差是一个表示实际值和预测值之间存在多大差异的数值。from sklearn.metrics import mean_squared_error mean_squared_error(y, y_pred)43.60055177116956决定系数决定系数(coefficient of determination)是使用均方误差来表示训练好的模型的预测效果的数 值,也就是被称为 R2 的系数。 当该系数取最大值 1.0 时,说明没有误差。它的值通常在 0.0 和 1.0 之间,但如果预测的误差过大,也可能为负值。换言之,该系数的值越接近 1.0,说明模型对数据点的解释能力越强。我们可以使用 r2_score 函数计算决定系数。from sklearn.metrics import r2_score r2_score(y, y_pred)0.48352545599133423均方误差和决定系数指标的不同前面解释了如何使用均方误差和决定系数两个指标评估回归问题。光看均方误差的数值不能判 断精度是好还是坏。如果目标变量的方差较大,均方误差也会变大。而决定系数可以使用不依赖于 目标变量方差的取值范围在 0.0 和 1.0 之间的值表示,所以即使目标变量的数量级不同,也可以将 决定系数作为一般的指标使用。与其他算法进行比较前面使用 LinearRegression 介绍了均方误差和决定系数,我们再来看一下使用其他算法的情况。下面使用 SVR 进行回归,并与使用 LinearRegression 时的情况进行比较。SVR 是将第 2 章介绍的支持向量机(核方法)应用于回归而得到的算法。from sklearn.svm import SVR model_svr_linear = SVR(C=0.01, kernel='linear') model_svr_linear.fit(X, y) y_svr_pred = model_svr_linear.predict(X)上面的代码导入了 SVR 类,用于训练和预测。下面在图 4-4 中查看使用 LinearRegression和 SVR 时的学习结果。%matplotlib inline import matplotlib.pyplot as plt fig, ax = plt.subplots() ax.scatter(X, y, color='pink', marker='s', label='data set') ax.plot(X, y_pred, color='blue', label='LinearRegression') ax.plot(X, y_svr_pred, color='red', label='SVR') ax.legend() plt.show()
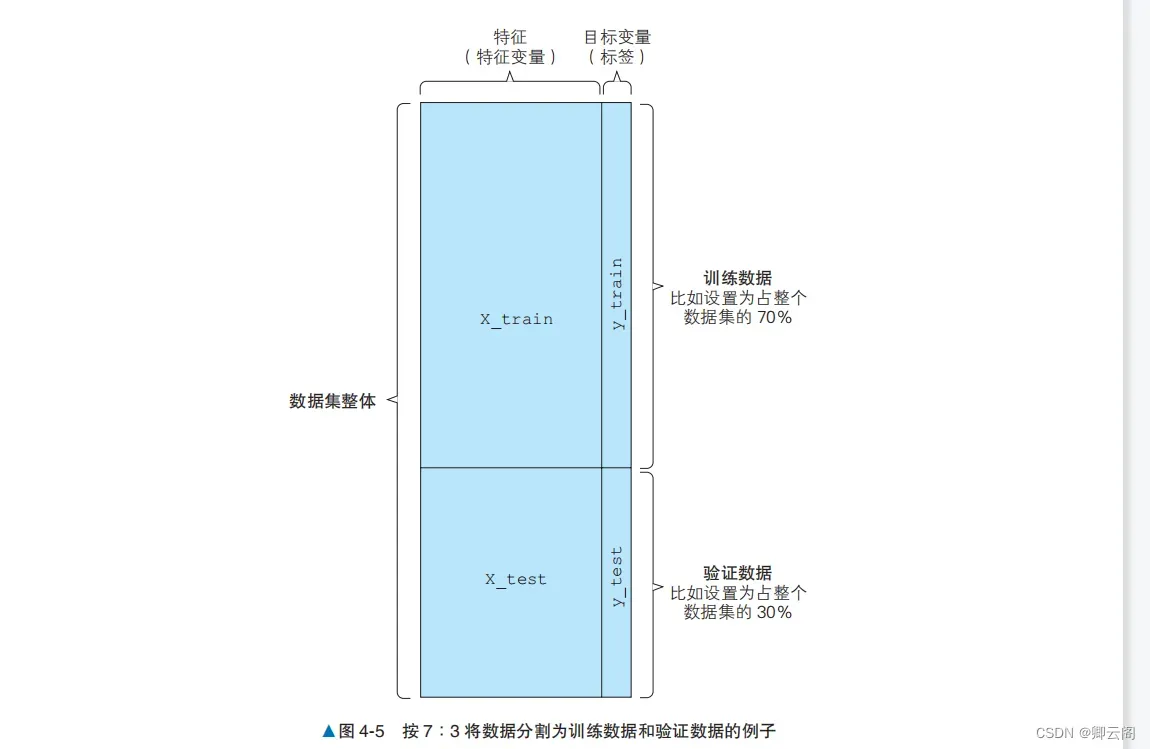
蓝线表示 LinearRegression,红线表示 SVR。从图中可以看出,SVR 的线和数据不太一致。下面看一下均方误差和决定系数的值。print(mean_squared_error(y, y_svr_pred)) # 均方误差 print(r2_score(y, y_svr_pred)) # 决定系数 print(model_svr_linear.coef_) # 斜率 print(model_svr_linear.intercept_) # 截距72.14197118147209 0.14543531775956597 [[1.64398]] [11.13520958]结果依次是均方误差、决定系数、斜率和截距。LinearRegression 的均方误差和决定系数分别约为 43.6 和 0.484,与之相比,SVR 的均方误差和决定系数都变差了,分别约为 72.1 和 0.145。 经过比较,我们发现 LinearRegression 的各个指标的值都更好。通过均方误差和决定系数,我们能够对模型进行定量评估。这个结果可能会给人以 SVR 不是一个好算法的印象。其实通过改变 SVR 的 C 和 kernel 参数,就可以改善 SVR 的均方误差和决定系数。超参数的设置下面将初始化 SVR 时的参数变更为 C = 1.0, kernel = ‘rbf’。model_svr_rbf = SVR(C=1.0, kernel='rbf') model_svr_rbf.fit(X, y) y_svr_pred = model_svr_rbf.predict(X) print(mean_squared_error(y, y_svr_pred)) # 均方误差 print(r2_score(y, y_svr_pred)) # 决定系数37.40032481992347 0.5569708427424378可以看出,均方误差和决定系数都得到了改善。C 和 kernel 是 SVR 的超参数。model_svr_rbf.coef_ 和 model_svr_rbf.intercept_ 等学习参数是由机器学习算法更新的,而超参数需要在训练开始前由用户给出。因此,如果超参数设置得不好,模型的性能就可能会很差。模型的过拟合下面来看一下模型的过拟合。使用以下代码将数据集分为训练数据和用来确认性能的验证数据,然后进行 SVR 的训练和预测train_X, test_X = X[:400], X[400:] train_y, test_y = y[:400], y[400:] model_svr_rbf_1 = SVR(C=1.0, kernel='rbf') model_svr_rbf_1.fit(train_X, train_y) test_y_pred = model_svr_rbf_1.predict(test_X) print(mean_squared_error(test_y, test_y_pred)) # 均方误差 print(r2_score(test_y, test_y_pred)) # 决定系数69.32813164021485 -1.4534559402985217虽然超参数没有变过,但模型在验证数据上的表现远差于在训练数据上的表现。这种对训练数 据的预测效果很好,但对验证数据(没有用于训练的数据)的预测效果不好的现象叫作过拟合。 在有监督学习中,防止过拟合是一个重要课题。仅仅考查之前介绍的各指标,并不足以判断模 型的好坏。重要的是在解决实际问题时,模型对未知数据的预测精度。模型对这种未知数据的预测 能力叫作泛化能力。即使模型对训练数据的均方误差很小,如果发生过拟合,泛化能力也会很低。 过拟合和超参数的设置是分类问题和回归问题的共同挑战。防止过拟合的方法有监督学习的特征值和目标变量是作为训练数据预先给出的。前面介绍了对训练数据的性能评 估方法。但在使用有监督学习解决实际问题时,除了评估模型对训练数据的性能之外,评估模型对 不包括在训练数据中的数据(未知数据)的性能也是非常重要的。以乳腺癌数据集为例,“患者的身体数据”(特征)和“恶性 / 良性”(目标变量)是训练数据。在实际应用中,对于“恶性 / 良性”不明的患者,重要的是能否通过患者的体检数据预测出“恶性 / 良性”。一个模型如果对训练数据的预测精度很高,但对未知数据不能进行很好的预测,那就不能说它是一个好模型。防止过拟合的方法有几种,以下是一些有代表性的方法。将数据分为训练数据和验证数据防止过拟合的一个代表性的方法是将数据分为训练数据和验证数据。换言之,这种方法不使用 事先给定的所有数据进行训练,而是留出一部分数据用于验证,不用于训练。 使用 scikit-learn 的 train_test_split 函数,我们可以很容易地分割数据。from sklearn.datasets import load_breast_cancer data = load_breast_cancer() X = data.data y = data.target from sklearn.model_selection import train_test_split X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3)训练用的特征值:X_train验证用的特征值:X_test训练用的目标变量:y_train验证用的目标变量:y_test我们将数据分为训练数据和验证数据,其中 70% 用于训练,30% 用于验证(图 4-5)。这个分 割比例设为多少是没有明确规定的。如果数据集很大,有足够的数据用于训练,将分割比例设置为 6∶4 也是可行的;反之,如果数据集太小,不能很好地进行训练,可以将分割比例设置为 8∶2 等。 另外要注意的是,每次运行时 train_test_split 的结果都是不同的,如果想保持结果固定,需要设置 random_state 参数。下面使用训练数据和验证数据来学习算法并创建模型。
from sklearn.svm import SVC model_svc = SVC() model_svc.fit(X_train, y_train) y_train_pred = model_svc.predict(X_train) y_test_pred = model_svc.predict(X_test) from sklearn.metrics import accuracy_score print(accuracy_score(y_train, y_train_pred)) print(accuracy_score(y_test, y_test_pred))
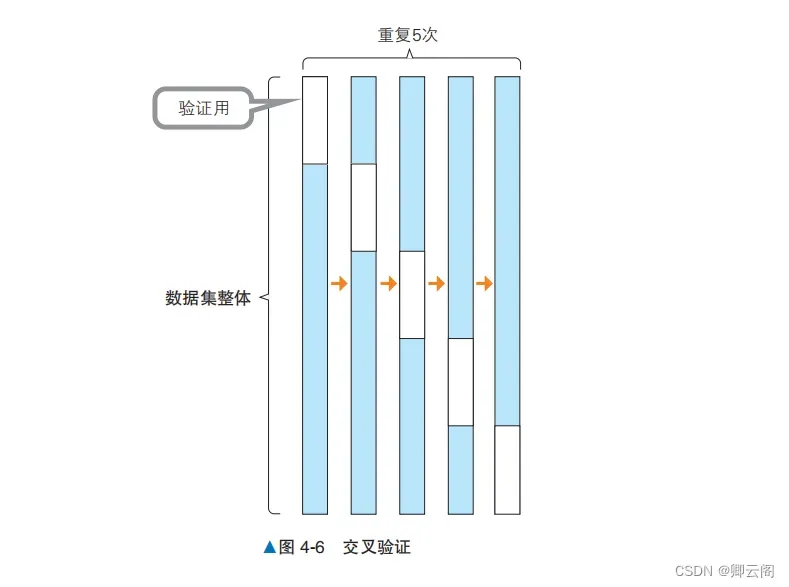
0.9020100502512562 0.9239766081871345如果与对训练数据的正确率相比,对验证数据的正确率要低很多,就说明数据发生了过拟合。上 面代码中的模型对未知数据的正确率约为 60%。下面使用另一个模型 RandomForestClassifier 来试一下。from sklearn.ensemble import RandomForestClassifier model_rfc = RandomForestClassifier() model_rfc.fit(X_train, y_train) y_train_pred = model_rfc.predict(X_train) y_test_pred = model_rfc.predict(X_test) from sklearn.metrics import accuracy_score print(accuracy_score(y_train, y_train_pred)) print(accuracy_score(y_test, y_test_pred))1.0 0.9707602339181286这次虽然对验证数据的正确率依然比对训练数据的低,却是约为 96% 的高正确率。由于模型 对验证数据的正确率也很高,所以可以说防止了过拟合。 从这些模型的结果来看,也许我们应该使用 RandomForestClassifier。在选择模型时, 如果没有分割数据,只看对训练数据的正确率,我们可能会选择 SVC。通过观察对验证数据的正确 率,我们能够避免使用出现了过拟合的模型。交叉验证即使在将数据分为训练数据和验证数据后进行评估,也依然可能发生过拟合。可以想到的原因是使用的训练数据和验证数据碰巧非常相似。反过来也有可能出现训练数据和验证数据非常不相似的情况。为了避免这种数据分割的误差,可以使用不同的分割方案进行多次验证,这就是所谓的交叉验证(cross validation)。本节以将数据分割 5 次,其中 80% 的数据用于训练,20% 的数据用于验证的情况为例进行说明。 如图 4-6 所示,每次获取不同的 20% 的数据作为验证数据,重复 5 次。在这个例子中,20% 的数据是按分组顺序分别分割的,但在实际应用中,作为验证数据的 20% 的数据是随机抽取的。以下代码非常轻松地将数据分成了 5 块,即运行 5 次,每次留下 20% 的数据用于训练后的验证。
from sklearn.model_selection import cross_val_score from sklearn.model_selection import KFold cv = KFold(5, shuffle=True) model_rfc_1 = RandomForestClassifier() cross_val_score(model_rfc_1, X, y, cv=cv, scoring='accuracy')
array([0.92105263, 0.96491228, 0.99122807, 0.95614035, 0.96460177])这时正确率会被输出 5 次。我们可以看到正确率有时很高,有时很低。在选择模型时,需要考 虑所有正确率的均值和方差。 另外,我们也可以输出 F 值的评估结果。通过将 cross_val_score 函数的 scoring 参数定义为 f1,就可以输出 F 值,代码如下所示array([0.96103896, 0.97101449, 0.99224806, 0.98113208, 0.94285714])搜索超参数前面介绍了如何使用分割得到的数据来选择不会出现过拟合的模型。如果在此基础上仔细地选择超参数,就可以进一步提高模型的性能。就像前面在“超参数的设置”部分介绍的那样,通过 反复设置一个超参数并检查其性能,最终可以得到更好的超参数。但是多个超参数的组合数量非常 多,逐一设置每个超参数的过程非常耗时。 本节将介绍搜索超参数的方法。使用网格搜索选择超参数网格搜索是一种自动搜索超参数的方法。如图 4-7所示,这是一种对各个超参数组合进行穷尽搜索的方法。需要注意的是,要搜索的超参数必须事先确定。下面是使用 scikit-learn 的 GridSearchCV 进行RandomForestClassifier 超参数搜索的示例代码。GridSearchCV 一边关注对验证数据的性能,一边执行超参数的搜索。首先加载数据。这里要做的是对分类任务进行网格搜索,所以要重新加载美国威斯康星州乳腺癌数据集。GridSearchCV(cv=KFold(n_splits=5, random_state=None, shuffle=True), estimator=RandomForestClassifier(), param_grid={'max_depth': [5, 10, 15], 'n_estimators': [10, 20, 30]}, scoring='accuracy')
from sklearn.datasets import load_breast_cancer data = load_breast_cancer() X = data.data y = 1 - data.target # 反转标签的0和1 X = X[:, :10]接下来进行网格搜索。from sklearn.ensemble import RandomForestClassifier from sklearn.model_selection import GridSearchCV from sklearn.model_selection import KFold cv = KFold(5, shuffle=True) param_grid = {'max_depth': [5, 10, 15], 'n_estimators': [10, 20, 30]} model_rfc_2 = RandomForestClassifier() grid_search = GridSearchCV(model_rfc_2, param_grid, cv=cv, scoring='accuracy') grid_search.fit(X, y)上面的代码为 max_depth 准备了 3 个值,为 n_estimators 也准备了 3 个值,对二者所有的组合,即 3×3=9 种情况进行了评估。下面输出所得到的最好的得分及相应的超参数值。print(grid_search.best_score_) print(grid_search.best_params_)0.9630336904207422 {'max_depth': 15, 'n_estimators': 30}除了交叉验证外,GridSearchCV 还支持使用 F 值进行评估。修改 GridSearchCV 的评估方法很简单,将 scoring 参数指定为 f1 即可。前面介绍了通过调整超参数等来防止过拟合的方法。除此之外,还有其他一些方法可以防止过拟合。下面列出防止过拟合的主要方法的名称。在应对过拟合时,也可以考虑这些方法。增加训练数据减少特征值正则化Early Stopping集成学习
文章出处登录后可见!
已经登录?立即刷新