人工智能（第三版）第二章 习题

讨论题：

1. 搜索为什么是 AI 系统的重要组成部分？

   搜索可以获取目标信息、有效信息

1. 状态空间图是什么？

   它是对问题的一种表示方法，它有很多条路径，某个具体问题的解将对应状态空间图中的一条路径

1. 描述生成-测试范式。

   先给出所有可能的解，然后再筛选出所有符合条件的解 

1. 生成器有什么属性？

   完备的、非冗余、知情的

1. 回溯法如何对完全枚举法进行改进？

   完全枚举法会查看所有可能的情况，即使当前步骤不能得到解，它也会继续往后搜索；而回溯法在当前步骤无法不能得到解时，会回溯到前一步， 寻找能够摆放当前步骤的位置，若找不到，则撤销前一步，以此往复。

1. 用一两句话描述贪心算法。

   贪心算法会将一个问题拆解成好几个步骤，然后找出当前步骤的最优解

1. 陈述旅行商问题

   给定n个顶点的加权图（即每条边上带有开销值），求从某个顶点Vi出发经过加权图中的所有顶点（每个顶点只经过一次），然后返回到Vi的最短路径

1. 简述 3 种盲目搜索算法。

   深度优先搜索（DFS）： 从起始顶点开始，沿着一条路径一直向下访问直到末端，然后回溯并继续探索下一条路径。

   广度优先搜索（BFS）：从起始顶点开始，首先访问起始顶点的所有相邻顶点，然后依次访问这些相邻顶点的相邻顶点，以此类推，直到所有顶点都被访问过。

   迭代加深的深度优先搜索（DFS-ID）：它会先以较浅的深度进行深度优先搜索，在搜索过程中若未找到目标，则逐渐增加深度限制，并重复进行深度优先搜索，直至找到目标为止

1. 在何种意义上，盲目搜索算法是盲目的？

   没有确定的目标，搜索方法是随机的抽取

1. 按照完备性、最优性和时空复杂性，比较本章描述的 3 种盲目搜索算法。

完备性：

      ·深度优先搜索：在所有路径都不是很深的情况下，DFS是完备；在某几条路径很长的情况下，DFS不是完备的

      ·广度优先搜索：如果搜索空间的分支因子是有限的，那么 BFS 是完备的

      ·迭代加深的深度优先搜索：如果给定的搜索空间是有限的，并且DFS-ID算法能够遍历所有可能的输入样本，那么它具有完备性。但是，如果搜索空间无限大或算法无法遍历所有输入样本，那么DFS-ID可能无法解决所有情况，从而导致不完备性。

1. 在什么情况下，DFS 比 BFS 好？

    树很深；分支因子不太大；并且解出现在树中的位置相对较深

1. 在什么情况下，BFS 比 DFS 好？

    搜索树的分支因子不太大（一个适度的 b 值），当整棵树的分支因子实际上很大时， BFS 会因为有过多的路径需要探索而不堪重负；解出现在树中的位置在合理的深度（一个适度的 d 值）；所有路径都不是特别深

1. 在什么意义上，可以说 DFS-ID 是 BFS 和 DFS 的折中？

在时间复杂度上，DFS-ID比BFS稍好；在空间复杂度上，它与DFS相同

练习题：

1. 在只允许称重 3 次的情况下，求解 12 枚硬币的假币问题。回忆一下，天平可以返回以下3种结果之一：相等、左侧轻或左侧重。
2. 在只称重两次的情况下，求解微型假币问题或证明这是不可能的。

   只称重两次只有在特定情况下能够求解

   当第一组和第二组的重量相同时，说明假币在第三组中，拿出第一组中的一枚硬币与第三组中的其中一枚比较，若重量相等则另一枚是假币，若重量不相等则这枚是假币 

1. 非确定性搜索（nondeterministic search）是本章未讨论的一种盲目搜索方法。在这种搜索中，刚刚扩展的子节点以随机顺序放在开放表中。请判断非确定性搜索是否完备以及是否最优。

   不是完备的。将扩展的子节点以随机顺序放在开放表中，无法保证在有限的步骤中找到解。

   不是最优的。由于节点扩展顺序是随机的，无法保证在最少的步骤中找到解。

1. n皇后问题的另一个生成器如下：第一个皇后放在第一行，第二个皇后不放在受第一个 皇后攻击的任何方格中。在状态 i，将第 i 列的皇后放在未受前面（i−1）个皇后攻击的方格中， 如图 2.34 所示。 （a）使用这个生成器求解 4 皇后问题。 （b）证明这个生成器比文中使用的两个生成器拥有更多的信息。 （c）画出搜索第一个解时在搜索树中展开的部分。

1. ：解是[1,3,0,2]和[2,0,3,1]
2. ：原本的生成器会将所有的情况都遍历一遍，而这个生成器会将明显会导致冲突的情况排除掉，缩小范围，降低运行成本

1. 思考下列 4 皇后问题的生成器：从 i=1 到 i=4，随机地分配皇后 i 到某一行。这个生成器完备吗？非冗余吗？解释你的答案。

   不完备也不是非冗余的。首先，这个生成器是随机地分配皇后的位置，这无法保证皇后遍历过每一个位置，造成不完备 ；其次，这个随机分配有可能分配到同一个地方，产生同一个解，造成冗余

1. 如果一个数等于其因数（不包括这个数本身）的和，则称这个数是完美数。例如，6 是 完美数，因为 6 = 1 + 2 + 3，其中整数 1、2 和 3 都是 6 的因数。给出你所能想到的拥有最多信息的生成器，使用这个生成器，可以找到 1 和 100 之间（包括 1 和 100 在内）的所有完美数。

def factor_sum(n):

    return sum(f for f in range(1, n) if n % f == 0)

perfect_numbers = [num for num in range(1, 101) if factor_sum(num) == num]

print(perfect_numbers)

1. 使用 Dijkstra 算法找到从源顶点 V0到所有其他顶点的最短路径，如图 2.35 所示。 图 2.34 4 皇后问题的生成器 图 2.35 使用 Dijkstra 算法的标记图

1. 创建拼图（如15拼图）的表示以适合检查重复状态。

   建立一个二维数组，在相应的位置标上号，若对应的是空位置，则标上0   

1. 使用广度优先搜索求解传教士与野人问题。  
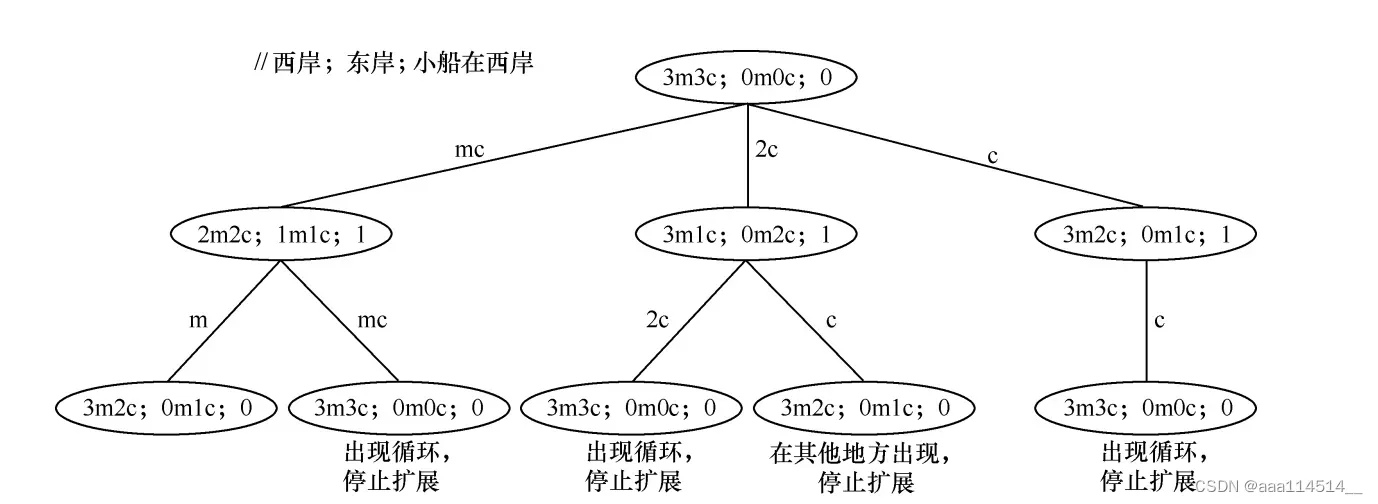
2. 在河的西岸，一个农夫带着一匹狼、一只山羊和一篮子卷心菜（参见图 2.0）。河上有一艘船，可以装下农夫以及狼、山羊、卷心菜三者中的一个。如果留下狼与羊单独在一起，那么狼会吃掉羊。如果留下羊与卷心菜单独在一起，那么羊会吃掉卷心菜。现在的目标是将它们都安全地转移到河的对岸。请分别使用以下搜索算法解决上述问题：（a）深度优先搜索；（b）广度优先搜索
3. 深度优先搜索：先把羊送过去，以这个为起点，然后继续搜索下去
4. 广度优先搜索：将把狼、山羊、卷心菜这三个东西都送过去的情况都遍历，这一层只有运送山羊的情况成功，接下来就如DFS一样遍历下去

1. 首先使用 BFS，然后使用 DFS，从图 2.36（a）和图 2.36（b）的起始节点 S 开始，最终到达目标节点 G。其中每一步都按照字母表顺序浏览节点。
2. 标记图 2.37 所示的迷宫。
3. 对于图 2.37 所示的迷宫，先使用 BFS，再使用 DFS，从起点处开始走到目标处。 图 2.36 使用 BFS 和 DFS 到达目标节点 图 2.37 迷宫
4. 我们已经确定，12枚硬币的假币问题需要对3组硬币进行称重才能确定假币。那么在 15 枚硬币中，需要称重多少次才可以确定假币？20 枚硬币时又会怎么样？请开发出一种算法来 证明自己的结论。 提示：可以先考虑 2～5 枚硬币所需的基本称量次数，从而开发出事实知识库，自底向上得 到这个问题的解。

15枚:4次

20枚：4次

先将所有的硬币等分成相同的个数，进行比较，然后再等分，直到找到假币为止     

1. 我们讨论了传教士与野人问题。假定“移动”或“转移”是强行（受迫）的，找出这个问题的一个解。确定问题解决状态的“子目标状态”，我们必须获得这个状态，才能解决这个问题