前言
终于从头到尾把鱼书看完啦,真的是非常入门,非常查漏补缺,对新手很友好,对有一定基础的人也非常不错。看完不复习等于没看,所以今天开始复盘,顺便写这篇读书笔记。希望分享给没看过这本书或者看过这本书的同僚们参考,欢迎大家指教。我将从第三章神经网络开始复习,前两章内容书里已经非常基础and清楚了。(会持续更新滴)
三、神经网络
3.2 激活函数
这一小节学习的概念是神经网络学习中非常重要的激活函数,它们都是一些非线性函数,至于为何是非线性函数,因为非线性函数组合才能实现复杂网络的构建。以下将实现三个激活函数,它们分别是阶跃函数、sigmoid函数和relu函数
3.2.1 阶跃函数
def step_function(x):
# if x > 0:
# y = 1
# else:
# y = 0
y = x > 0
y = y.astype(np.int)
return y
这就是阶跃函数的代码实现,可以了解到阶跃函数就是当自变量大于零的时候等于1,小于零的时候等于0的函数,注释上面的改写成下面的原因是,为了numpy数组更方便进行后续操作。
x = np.array([1.5,-2,5.0])
step_function(x)
输出为array([1, 0, 1])
x1 = np.arange(-6,7,1)
y1 = step_function(x1)
plt.plot(x1,y1)
plt.show()
输出的图像为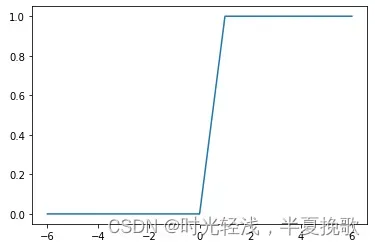
3.2.2 sigmoid函数
def sigmoid(x):
y = 1/(1+np.exp(-x))
return y
sigmoid函数是1/(+exp(-x))的形式,当输入是numpy数组的时候,用上面的代码就可实现了。
sigmoid(x):
输出为array([0.81757448, 0.11920292, 0.99330715])
x1 = np.arange(-6,7,1)
y2 = sigmoid(x1)
plt.plot(x1,y2)
plt.show()
输出的图像为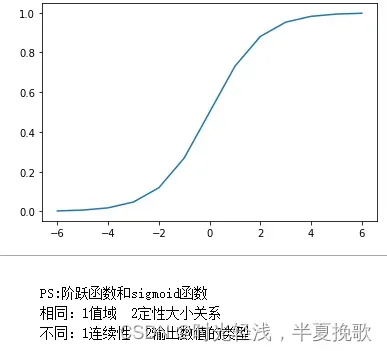
3.2.3 ReLU函数
def ReLU(x):
y = np.maximum(0,x)
return y
ReLU函数相当于在自变量小于0的时候为0,大于零的时候和自变量相等,也就是在自变量和0中取最大值,如上代码即可实现。
ReLU(x)
输出为array([1.5, 0. , 5. ])
x1 = np.arange(-6,7,1)
y3 = ReLU(x1)
plt.plot(x1,y3)
plt.show()
输出图像为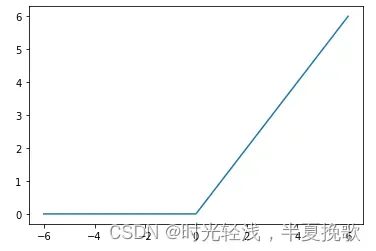
以上小节激活函数,为什么激活函数不能是线性函数呢?如果使用线性函数,加深神经网络的层数就没有意义了。
3.3 多维数组
numpy多维数组的相关运算对于神经网络的实现是基本操作。
3.3.1 多维数组的维度和形状
a = np.array([[2,4,5],[2,3,9]])
a.ndim #维度 将会输出2
a.shape #形状 将会输出(2,3)
b = np.array([[2,2,1],[2,2,4],[5,4,4]])
b.ndim #维度 将会输出2
b.shape #形状 将会输出(3,3)
3.3.2 多维数组的点乘
np.dot(a,b) #维度要符合矩阵乘法,左列等于右行;不然就要符合广播机制
输出为array([[37, 32, 38],
[55, 46, 50]])
3.4 三层神经网络的实现
3.4.1 一步一步进行
第一层,大概逻辑是输入×权重加偏置,然后激活函数
X = np.array([1.0,0.5])
W1 = np.array([[0.1,0.3,0.5],[0.2,0.4,0.6]])
B1 = np.array([0.1,0.2,0.3])
print(X.shape)
print(W1.shape)
print(B1.shape)
输出为(2,)
(2, 3)
(3,)
A1 = np.dot(X,W1) + B1
print(A1)
输出为[0.3 0.7 1.1]
Z1 = sigmoid(A1)
print(Z1)
输出为[0.57444252 0.66818777 0.75026011]
第二层,和第一层的逻辑
W2 = np.array([[0.1,0.4],[0.2,0.5],[0.3,0.6]])
B2 = np.array([0.1,0.2])
A2 = np.dot(A1,W2) + B2
print(A2)
输出为[0.6 1.33]
Z2 = sigmoid(A2)
print(Z2)
输出为[0.64565631 0.79084063]
第三层,前面逻辑一样,激活函数那里用的恒等函数,回归用恒等,分类下一节介绍
W3 = np.array([[0.1,0.3],[0.2,0.4]])
B3 = np.array([0.1,0.2])
A3 = np.dot(A2,W3) + B3
print(A3)
输出为[0.426 0.912]
def identity_function(x):
y = x
return y
Z3=identity_function(A3)
print(Z3)
输出为[0.426 0.912]
回归问题的输出层的激活函数为恒等函数,下一节详细介绍
3.4.2 合起来实现
先构建一个初始化参数的函数,如下:
def init_network():
network = {}
network['W1'] = np.array([[0.1,0.3,0.5],[0.2,0.4,0.6]])
network['W2'] = np.array([[0.1,0.4],[0.2,0.5],[0.3,0.6]])
network['W3'] = np.array([[0.1,0.3],[0.2,0.4]])
network['B1'] = np.array([0.1,0.2,0.3])
network['B2'] = np.array([0.1,0.2])
network['B3'] = np.array([0.1,0.2])
return network
然后构建一个前进函数,如下:
def forward(network,x):
W1,W2,W3 = network['W1'],network['W2'],network['W3']
B1,B2,B3 = network['B1'],network['B2'],network['B3']
A1 = np.dot(x,W1) + B1
Z1 = sigmoid(A1)
A2 = np.dot(Z1,W2) + B2
Z2 = sigmoid(A2)
A3 = np.dot(Z2,W3) + B3
Z3 = identity_function(A3)
return Z3
接着传入输入,观察参数通过网络的情况
network=init_network()
x=np.array([1.0,0.5])
y=forward(network,x)
print(y)
输出为[0.31682708 0.69627909]
3.5 输出层的设计
3.5.1 Softmax函数
激活函数的使用,回归问题用恒等函数,分类问题用softmax函数
def softmax(x):
exp_x = np.exp(x)
sum_exp_x = np.sum(exp_x)
y = exp_x / sum_exp_x
return y
softmax函数的函数形式相当于是自然指数除以自然之数求和
x = np.array([0.3,2.9,4.0])
y = softmax(x)
print(y)
输出为[0.01821127 0.24519181 0.73659691]
x = np.array([1010,1000,990])
y = softmax(x)
print(y)
输出为[nan nan nan]
为了解决数组中的大数的输入无法处理的问题,将softmax函数优化为下面这样,在传入自然指数的时候减去数组中的最大值,得到的函数定义代码如下:
def softmax(x):
c = np.max(x)
exp_x = np.exp(x-c)
sum_exp_x = np.sum(exp_x)
y = exp_x / sum_exp_x
return y
x = np.array([1010,1000,990])
y = softmax(x)
print(y)
输出为[9.99954600e-01 4.53978686e-05 2.06106005e-09],至此解决了softmax函数的大数输入问题
3.5.2 Softmax函数的特征:输出值求和为1,符合概率分布问题
sum_y = np.sum(y)
print(sum_y)
输出为1.0,因此对于分类问题的输出都是需要进行这样的softmax操作,规范输出的求和符合1.0
四、神经网络的学习
4.2 损失函数
4.2.1 均方误差MSE
4.2.2 交叉熵误差CEE
4.2.3 mini-batch上的交叉熵的实现
4.3 数值微分
4.4 梯度
4.5 学习算法的实现
总结
第三章到第七章将会以书上的基础内容总结为主,第八章争取找一些新东西(那些没有代码示例,但似乎很有趣的概念和算法)加进读书笔记里。
希望这一次的读书笔记不要半途而废,每天总结一小部分,积少成多,希望早日完结撒花~
文章出处登录后可见!
