1. 神经网络介绍

神经网络的定义：人工神经网络（Artificial Neural Networks，简写为ANNs）也简称为神经网络（NNs）或称作连接模型（Connection Model），它是一种模仿动物神经网络行为特征，进行分布式并行信息处理的算法数学模型。这种网络依靠系统的复杂程度，通过调整内部大量节点之间相互连接的关系，从而达到处理信息的目的。

1.1 神经网络的生物学背景

• 神经细胞的工作机制
  神经元理论（neurons theory）：神经细胞之间是相互独立的，通过某种形式传递信号。

• 神经元学说
  (1) 神经网络由许多独立的神经细胞个体（“神经元”），通过神经元之间的接触点联接而成；
  (2) 所有神经元都具有不对称的极性结构：一边有一枝很长的“轴突”纤维状突起，另一边有许多“树突”。树突(dendrites) 是接收其他神经元输入信息的结构，而 轴突(axon) 则是神经元将信息传向远方的输出结构；
  (3) 基于神经组织的发育、退化和再生的结构变化，卡哈尔 还首先提出了神经联接的可塑性概念；
  (4) 树突接收信息，触发区整合电位，产生神经冲动，末端的突触为输出区，从而向下一个神经元传递。人脑神经系统包含近860亿个神经元，每个神经元有千个突触(synapse)。

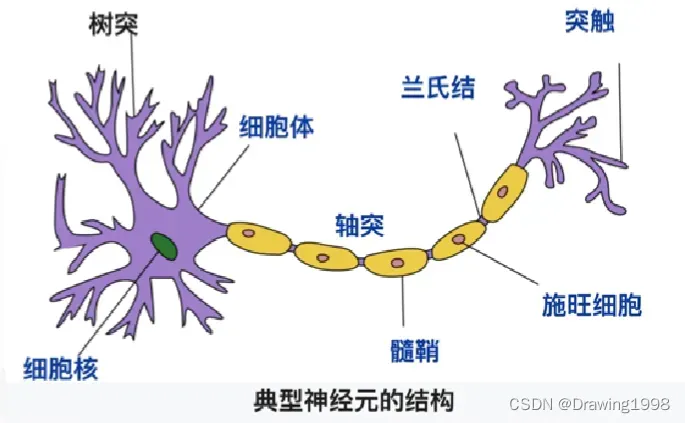
• 生物神经网络的假定特点：
  (1) 每个神经元都是一个 多输入单输出 的信息处理单元；
  (2) 神经元输入 分 兴奋性输入 和 抑制性输入 两种类型；
  (3) 神经元具有 空间整合特性 和 阈值特性；
  (4) 神经元输入与输出间有固定的 时滞，主要取决于突触延搁

1.2 人工神经元与感知机

1943年心理学家 W.S.McCulloch 和 数理逻辑学家 W.Pitts 提出 按照生物神经元的结构和工作原理构造出来的抽象和简化模型—— M-P模型。此类模型通常将神经元形式化为一个「激活函数复合上输入信号加权和」的形式。

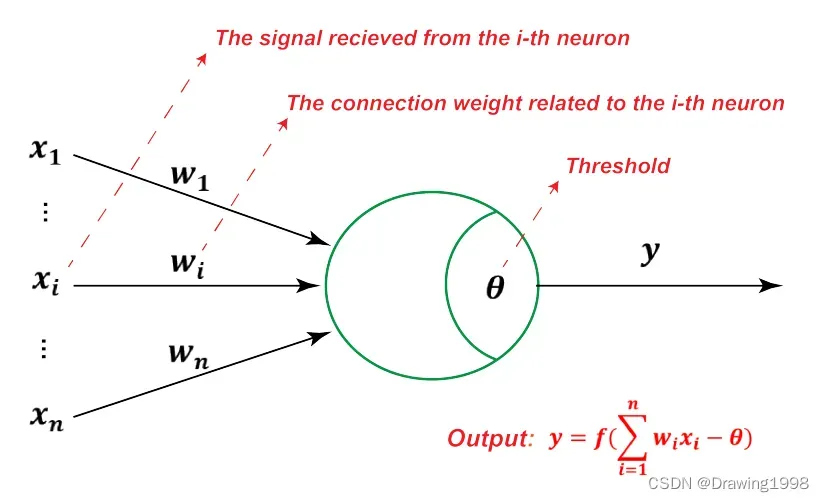
M-P 模型接收到来自 个其他神经元传递过来的输入信号 ，这些输入信号通过带权重的连接 进行传递，神经元接收到的总输入值 将与 神经元的阈值 进行比较，然后通过激活函数 处理以产生神经元的输出。即：
其中， 表示来自其他神经元的信号， 表示对应的连接权重， 表示神经元的阈值， 表示通常连续可微的激活函数(Activation Function)（或称 转移函数(Transfer Function)）。

• 神经元激活与否取决于阈值水平 ，即只有当其输入总和超过阈值 时，神经元才被激活而发放脉冲，否则神经元不会发生输出信号。
• 当神经元被激活时，称该神经元处于激活状态或兴奋状态，反之称神经元处于抑制状态。

1.3 常用激活函数

1.3.1 线性函数（Linear Function）

1.3.2 斜面函数（Ramp Function）

1.3.3 阈值函数（Threshold Function）

1.3.4 sigmoid函数

Sigmoid函数 是一个在生物学中常见的S型函数，也称为S型生长曲线。在信息科学中，由于其单增以及反函数单增等性质，Sigmoid函数常被用作神经网络的激活函数，将变量映射到0,1之间。

sigmoid函数 也叫 Logistic函数，用于隐层神经元输出，取值范围为(0,1)（0表示“抑制”，1表示“兴奋”），它可以将一个实数映射到(0,1)的区间，可以用来做二分类。在特征相差比较复杂或是相差不是特别大时效果比较好。Sigmoid作为激活函数有以下优缺点：

• 优点：平滑、易于求导。
• 缺点：激活函数计算量大，反向传播求误差梯度时，求导涉及除法；反向传播时，很容易就会出现梯度消失的情况，从而无法完成深层网络的训练。

Sigmoid 函数定义：

对 进行求导：

Sigmoid函数的图形：

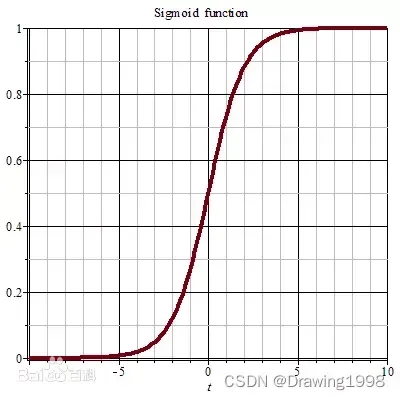
1.3.5 双曲正切函数（tanh函数）

函数图像为：

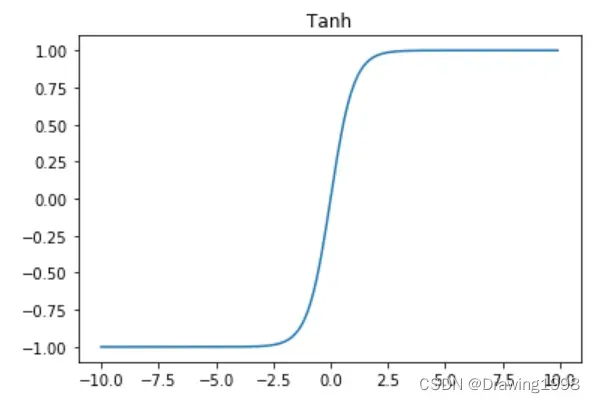
sigmoid函数 和 tanh函数 是研究早期被广泛使用的2种激活函数。两者都为S 型饱和函数。 当 sigmoid 函数 输入的值趋于正无穷或负无穷时，梯度会趋近零，从而发生梯度弥散现象。sigmoid函数 的输出恒为正值，不是以零为中心的，这会导致权值更新时只能朝一个方向更新，从而影响收敛速度。tanh 激活函数是 sigmoid 函数的改进版，是以零为中心的对称函数，收敛速度快，不容易出现 loss 值晃动，但是无法解决梯度弥散的问题。2个函数的计算量都是指数级的，计算相对复杂。softsign 函数是 tanh 函数的改进版，为 S 型饱和函数，以零为中心，值域为（−1，1）。

为什么 LR 模型要使用 sigmoid 函数，背后的数学原理是什么？

1.3.6 ReLU (Rectified Linear Regression，整流线性单元)

在现代神经网络中，默认的推荐是使用 由激活函数 定义的 整流线性单元 (Rectified Linear Regression) 或者称为 ReLU。

通常意义下，线性整流函数指代数学中的斜坡函数，即 。
而在神经网络中，线性整流作为神经元的激活函数，定义了该神经元在线性变换 之后的非线性输出结果。换言之，对于进入神经元的来自上一层神经网络的输入向量 ，使用线性整流激活函数的神经元会输出 。

2. 单层感知机（单层神经网络，线性回归）

2.1 单层感知机模型

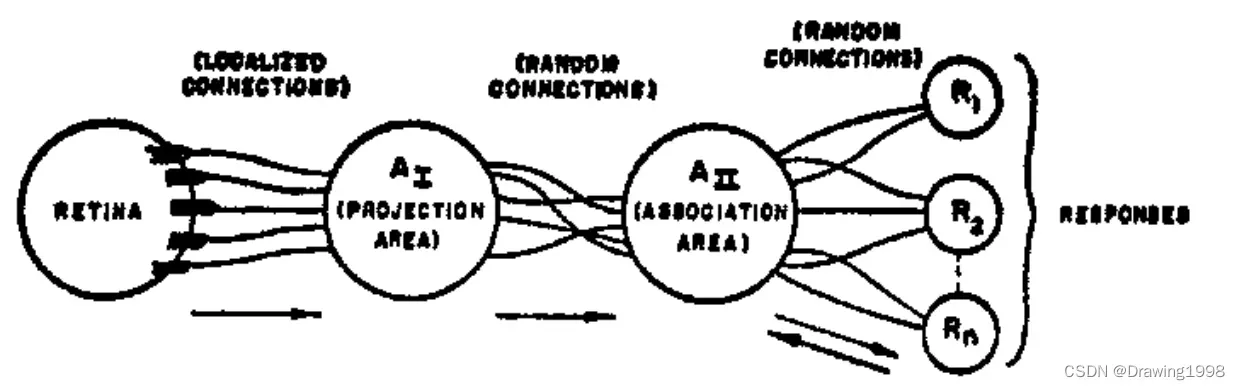
1957年，Frank Rosenblatt 结合 M-P模型 和 Hebb学习规则 发明了 感知机(perceptron)，两层神经网络，结构与MP模型类似，一般视为最简单的人工神经网络。

感知机 与 MP模型 的区别：输入不是离散的 0/1，激活函数不一定是 阈值函数。

感知机模型的组织结构如下：