前言

最近在复习线代，写了一份思维导图，打算分享一下有下载MindLine思维导图的朋友可以打开一下文件，文末可以下载

矩阵

定义

矩阵(matrix):一种存储数据的数阵,最早在线性方程组中,如:

$\left\{\begin{aligned}x_1+2x_2+5x_3 =7\\2x_1+3x_2+1x_3=8\end{aligned}\right.\Rightarrow A=\begin{pmatrix} 1&2&5\\2&3&1\end{pmatrix},B=\begin{pmatrix} 1&2&5&7\\2&3&1&8\end{pmatrix}$

我们称A为系数矩阵(cofficient matrix),B为增广矩阵(augment matrix)

同时，我们习惯在矩阵 $A_{m\times n}$ 下方表示矩阵形状,如上述 $A_{2\times 3}$ 表示矩阵形状2行3列

运算

矩阵转置

主对角线元素(下标为ii即元素所在的位置行数等于列数,如 $a_{22}\ a_{33}\ ...$ )

$\begin{pmatrix} a_{11}&...&a_{1j}\\ ...&\ &...\\ a_{i1}&...&a_{ij}\\ \end{pmatrix}^{T}=\begin{pmatrix} a_{11}&...&a_{i1}\\ ...&\ &...\\ a_{1j}&...&a_{ji}\\ \end{pmatrix}\\$

加法

要求矩阵形状一致,然后对应元素相加

$\begin{pmatrix} a_{11}&...&a_{1n}\\ ...&\ &...\\ a_{n1}&...&a_{nn}\\ \end{pmatrix}+\begin{pmatrix} b_{11}&...&b_{1n}\\ ...&\ &...\\ b_{n1}&...&b_{nn}\\ \end{pmatrix}=\begin{pmatrix} a_{11}+b_{11}&...&a_{1n}+b_{1n}\\ ...&\ &...\\ a_{n1}+b_{n1}&...&a_{nn}+b_{nn}\\ \end{pmatrix}$

数乘

常数k分配到矩阵中的每一个元素

$k\times\begin{pmatrix} a_{11}&...&a_{1n}\\ ...&\ &...\\ a_{n1}&...&a_{nn}\\ \end{pmatrix}=\begin{pmatrix} ka_{11}&...&ka_{1n}\\ ...&\ &...\\ ka_{n1}&...&ka_{nn}\\ \end{pmatrix}\\$

乘法

$A_{m\times n}\times B_{n\times k}=C_{m\times k}$ ，其中C中的元素

$c_{mk}=\begin{aligned}\sum_{j=1}^{n} a_{mj}b_{jk}\end{aligned}$

分块

矩阵的行列式计算时可以将块矩阵当成整体计算,下面会详细介绍

共轭

矩阵中的元素实部不变，虚部变为原来的相反数

$A=\begin{pmatrix} a_{11}+b_{11}i&...&a_{1n}+b_{1n}i\\ ...&\ &...\\ a_{n1}+b_{n1}i&...&a_{nn}+b_{nn}i\\ \end{pmatrix},then\ \overline{A}=\begin{pmatrix} a_{11}-b_{11}i&...&a_{1n}-b_{1n}i\\ ...&\ &...\\ a_{n1}-b_{n1}i&...&a_{nn}-b_{nn}i\\ \end{pmatrix}\\$

共轭转置

共轭转置本质上就是两种运算的结合，一种是共轭，另一种是转置，符号记为 $A^H$

$A^H=(\overline{A})^T$

$A=\begin{pmatrix} a_{11}+b_{11}i&...&a_{1n}+b_{1n}i\\ ...&\ &...\\ a_{n1}+b_{n1}i&...&a_{nn}+b_{nn}i\\ \end{pmatrix},then\ A^{H}=\begin{pmatrix} a_{11}-b_{11}i&...&a_{n1}-b_{n1}i\\ ...&\ &...\\ a_{1n}-b_{1n}i&...&a_{nn}-b_{nn}i\\ \end{pmatrix}\\$

特殊矩阵(补)

对称矩阵

$A^{T}=A$
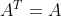
埃尔米特矩阵

$A^{H}=A$
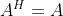
正交矩阵

$A^{T}A=E$
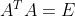
带状矩阵

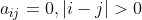
$a_{ij}=0,|i-j|>0$
酉矩阵

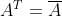
$A^{T}=\overline{A}$
上下三角矩阵

$|A|=\prod_{i=1}^{n}a_{ii}$

相似矩阵

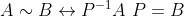
$A\sim B\leftrightarrow P^{-1}A\ P=B$
相合矩阵

$C^{H}A\ C=B$ ,若C为实矩阵非复矩阵时，关系为合同

范德蒙(Vandermonde)矩阵

每一列或行呈几何级数关系,其行列式的值为:

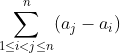
$\begin{aligned}\sum_{1\leq i<j\leq n}^{n}(a_j-a_i)\end{aligned}$
对角矩阵(diagonal matrix)

也叫标量阵

夹克比矩阵(Jacobian matrix)

存储函数的偏导数

旋转矩阵(Rotation matrix)

元素为三角函数

矩阵分解(补)

1.LU分解:

A=LU,L为为下三角,U为上三角

2.谱分解:

$A=P^{-1}\Lambda P$ ,其中，P为特征向量矩阵， $\Lambda$ 为特征值矩阵
3.SVD分解:

$A_{m\times n}=U_{m\times m}\Lambda_{m\times n} V_{n\times n}^{*}$ (A为共轭对称矩阵)
4.取用其中AA^{T}非零特征值并存入

$\begin{aligned} \Lambda&=PAP^{T}\\ AA^{T}&=U\Lambda_{1}U^{T}\\ A^{T}A&=V\Lambda_{2}V^{T}\\ \end{aligned}\\$
5.满秩分解

$A_{m\times n}=C_{m\times r}$ (列满秩) $\times$ $D_{r\times n}$ (行满秩)(先将A化简成最简矩阵B，接着取B前rank(秩)行作为D,再取每行首个非零元所在列构成C)
6.LUP分解

在LU分解前提下

矩阵的幂求法

在平常A $\times$ A还是可以计算，可当矩阵变为更为复杂如 $A^{100}$ 此时就需要一些技巧计算

1.对角化: $A^{n}=PB^{n}P^{-1}$ ,B为对角阵
2.幂零矩阵:将矩阵拆分成一个纯量阵以及幂零矩阵( $\exists k \ and \ matrix\ N\ so\ that\ N^{k}=0$ ,N叫做幂零矩阵,k叫做N的度数或指数),即: $A=\lambda E+B,\exists B^{k}=0$
3.行列拆分:若矩阵每一行(列)成几何级数关系 $\begin{pmatrix}r_{1}\\r_{2}\\...\\r_{n}\end{pmatrix}$ ,我们可以有 $A=\begin{pmatrix}1\\\frac{r_{2}}{r_{1}}\\...\\\frac{r_{n}}{r_{1}}\end{pmatrix}\begin{pmatrix}a_{11}\ a_{12}\ ...\ a_{1n}\end{pmatrix}$

4.分块矩阵:

$\begin{pmatrix}3 &4 &0&0\\4&-3&0&0\\0&0&-1&0\\0&0&0&2\end{pmatrix}^{n}\rightarrow\begin{pmatrix}\begin{pmatrix}3&4\\4&-3\end{pmatrix}^{n}&0\\0&\begin{pmatrix}-1&0\\0&2\end{pmatrix}^{n}\end{pmatrix}$

5.找规律
6.Hamilton-Cayley定理:

由 $f(\lambda)=|\lambda E-A|=\lambda^{n}+b_{1}\lambda^{n-1}+...+b_{n-1}\lambda+b_{n}$ 特征多项式,

那么我们有 $f(A)=A^{n}+b_{1}A_{n-1}+...+b_{n-1}A+b_{n}E=0$ 联立递归可得结果

逆矩阵

伴随矩阵

符号: $A^{*}$ 形式:

$A^{*}=\begin{pmatrix}A_{11}&...&A_{1n}\\...&&...\\A_{n1}&...&A_{nn}\end{pmatrix}$ , $A_{ij}$ 为除原矩阵i行j列元素组成的行列式\\
性质: $AA^{*}=|A|$

基础概念

概念:已知AB=E,那么AB这种关系类似实数里面的倒数关系，因此引入矩阵中逆的概念,B=A^{-1}\\
条件:方阵(非奇异矩阵)且矩阵的行列式子不为0
性质:

$\\1.|A^{-1}|=|A|^{-1}\\\\2..|A|\neq0$

广义逆矩阵(伪逆）

概念:奇异矩阵还有非方阵没有逆，但有伪逆

左逆矩阵: $A^{L}A=E$ 但不满足 $AA^{L}=E,A^{L}$ 称为左逆矩阵\\
$A^{L}A=E\xrightarrow[Least\ square\ method,AX=Y]{m\geq n,Column Full Rank}A^{L}=(A^{T}A)^{-1}A^{T}E=(A^{T}A)^{-1}A^{T}$

Column full rank:列满秩,Least square method:最小二乘法

右逆矩阵: $AA^{R}=E$ 但不满足 $A^{R}A=E,A^{R}$ 称为右逆矩阵\\
$AA^{R}=E\xrightarrow[Least\ square\ method,AX=Y]{n\geq m,Row Full Rank}A^{R}=A^{T}(A^{T}A)^{-1}E=A^{T}(A^{T}A)^{-1}$

伪逆矩阵: $n=m,A_{m\times n}$ 的秩为 $r\leq m=n$ ,通过SVD分解，我们有 $A=U\sum V^{T}$ ,则伪逆 $A^{+}=V\sum\ ^{+}U^{T}$ , $\sum\ ^{+}$ 中每个值为 $\sum$ 中每个值的倒数

最小二乘法(补)

$\\AX=Y\\ A=(X^{T}X)^{-1}X^{T}Y\\ A=\begin{pmatrix}k\\b\end{pmatrix},X=\begin{pmatrix}x&1\end{pmatrix}$

初等变换

初等矩阵:单位阵仅经过一次初等变换得到的矩阵(其逆为本身)

类别: $|A^T|=|A|$

1. $r_i\leftrightarrow r_j$ : $r_1$ 与 $r_2$ 互换

2. $r_i+kr_j$ : $r_j$ 的k倍加到 $r_i$

3. $kr_i$ : $r_i$ 乘以k倍

左乘初等矩阵为行变换，右乘为列变换

解方程AX=B

1.初等变换(A|B)~(E|X)

2.逆:X= $A^{-1}$ B

3.最小二乘法: $X=A^{T}(AA^{T})^{-1}B$

行列式

概念

是一种函数

性质

1. $|A^T|=|A|$

2. $|A|^{-1}=|A^{-1}|$

3.推论: $\exists r_{i}\vee c_{j}$ 全为0 $\rightarrow$ 行列式值为0

4.加法:只有一行或一列不同,才可以加减，满足后不同的那一行或列进行加减运算

5.三种变换

$\\r_{1}\leftrightarrow r_{2}$ : $r_1$ 与 $r_2$ 互换位置,行列式前添负号
$r_{1}+k\times r_{2}$ : $r_1$ 加上 $r_{2}$ 的k倍,行列式值不变
$k\times r_{1}$ : $r_1$ 变为原来的k倍,行列式值变为原来的 $\frac{1}{k}$ 倍

计算方法

二阶:

$\begin{vmatrix} a & b\\ c & d\\ \end{vmatrix}=ad-bc$

三阶:

$\begin{vmatrix} a_{11}&a_{12}&a_{13}\\ a_{21}&a_{22}&a_{23} \\ a_{31}&a_{32}&a_{33} \\ \end{vmatrix}$ = $(a_{11}a_{22}a_{33}+a_{12} a_{23} a_{31}+a_{21}a_{32} a_{13} )$ – $(a_{13} a_{22} a_{31} +a_{23} a_{32} a_{11} +a_{12} a_{21} a_{33} )$

$\\\begin{aligned} = \sum_{i=1}^{3} ((-1)^{i+j}a_{ij}A_{ij})=\sum_{j=1}^{3}((-1)^{i+j}a_{ij}A_{ij})\\~\\\end{aligned}\\~$ $=\begin{vmatrix} b_{11}&b_{12}&b_{13}\\ 0&b_{22}&b_{23} \\ 0&0&b_{33} \\ \end{vmatrix}=b_{11}b_{22}b_{33}$

高阶行列式:采用行列展开降阶或者化为三角阵

向量

定义

向量定义:向量是空间中一组有大小有方向的线段

线性

定义

线性组合定义:已知空间中的一组基底，向量空间中的任意向量都可用基底表示
线性表示定义: $\beta=\alpha x_n$ ,即 $\beta$ 用 $\alpha$ 线性表示

线性相关与线性无关的定义:两个向量间一个向量可以用另一向量表示就叫做线性相关,而一个向量组中一个向量可以用向量组内的其它向量表示就叫做向量组线性相关，反之，线性无关

向量组等价:向量组内的向量经过一系列线性变换(加减乘)后得到的新向量组，新旧两个向量组的关系就叫做向量组等价
行秩大小=列秩大小

矩阵的秩

定义:描述矩阵线性无关组的一个量,任取矩阵的i行i列 $(i\leq m,i\leq n)$ ,找到交叉项，取出来组成矩阵 $T_{i\times i}$ ，计算行列式 $|T_{i\times i}|$ ，若 $|T_{i\times i}|\neq0,|T_{(i+1)\times (i+1)}|=0$ ,则称矩阵的秩为i,通常记为r

求法:化为梯矩阵，数非零行行数

极大线性无关组:
将矩阵化成梯矩阵\rightarrow找到每行首个非零元\rightarrow将每行首个非零元所在的列找出来就是最大线性无关组

线性相关性质

1.对应行列式为0
2.r<m

线性相关与线性无关的分辨方法

1.行列式: $|A|=0\rightarrow$ 矩阵A中的向量组线性相关
2.秩:梯矩阵非零行行数 $r<m\rightarrow$ 矩阵A中的向量组线性相关
3.比值:向量 $r_1$ 与 $r_2$ 有 $\frac{r_1}{r_2}=C(C\ is\ a\ constant)\rightarrow$ 矩阵A中的向量组线性相关

向量空间

n维向量空间: $a\in R^{n},b\in R^{n}\rightarrow(a+b)\in R^{n}$
子空间:属于向量空间的一部分
基底:空间中所有的向量都可以用基底向量组线性表示
维数:矩阵的秩
坐标:以一个固定点0进行观测的向量

基变换

设原基底 $A=(\alpha_1\ \alpha_2\ ...)$ , 新基底B= $(\beta_1\ \beta_2\ ...)$
过渡矩阵:P= $B^{-1}$
基变换公式:B=PA
坐标变换公式:(新坐标)=P $\times$ (旧坐标)

内积与线性无关向量组的正交规范化

内积:对应维数相乘在求和,俩向量内积为零则说明俩向量正交
线性向量无关组正交规范化的施密特(Schimit)方法:
Step1:

$\beta_1=\alpha_1,\\$
Step2:

$\beta_2=\alpha_2-\frac{a_1,\beta_1}{(\beta_1,\beta_1)}\beta_1$

…
重复Step2直到 $\beta$ 数量到了n
Step3:

$\begin{aligned}\beta_n=\alpha_n-\sum_{i=1}^{n}\frac{a_i,\beta_i}{(\beta_i,\beta_i)}\beta_i\end{aligned}\\$
规范正交基:基底向量的膜长(norm)为1,正交矩阵:矩阵的列向量组成为规范正交基,俩俩正交

线性方程组

定义

解空间:包含了线性方程所有解的情况,解空间的解都可以由基础解析线性表示

Crammer法则

设有系数矩阵A,X变量与常量B形成AX=B关系,D=|A|, $D_i$ 为将B向量替换掉A中的i列,解得X:
$X=\begin{pmatrix}\frac{D_1}{D}\\\\\frac{D_2}{D}\\\\...\\\\\frac{D_n}{D}\end{pmatrix}\\$

解的情况

下面两种判断解情况可以通过行列式(方阵):
齐次线性方程组 $A_{m\times n}X=0$ 解的情况:1.零解rank(A)=m;2.通解rank(A)<m
非齐次线性方程AX=B解的情况:
1.无解:rank(A)<rank(A|B)
2.唯一解:rank(A)=rank(A|B)=n
3.通解:rank(A)=rank(A|B)<n

线性方程组解的结构与性质

1.基础解系间彼此线性无关
2.非齐次线性方程的解由齐次的通解 $\eta$ 加非齐次的特解 $\zeta$ :
$\\A\eta=0,A\zeta=B\rightarrow A(\eta+\zeta)=B\\ X=(\eta+\zeta)$

解(非)齐次线性方程的过程

Step1:用初等行变换化增广矩阵为梯矩阵，判断解是否存在
Step2:继续初等行变换化梯矩阵为最简梯矩阵
Step3:写出通解
Step4:化解通解为基础解系形式

特征值与特征向量

概念

为了求矩阵的幂 $A^n$ ,平常正常计算步骤太繁琐,因此猜想有没有什么结构能使计算变得简单,若有矩阵P(P可逆)使得 $A=P\Lambda P^{-1}$ ，( $\lambda$ 为一个数值),为了求解我们变换式子 $\\AP=P\lambda=\lambda P$ ,我们得到特征多项式: $(A-\lambda E)P=0$ ,我们称 $\lambda$ 的解为特征值，在对应的特征值下的解系，叫做特征向量，利用这个我们得到Hamilton-Cayley定理(在幂求解法有提到)
$tr(A)=\begin{aligned}\sum_{i=1}^{n}\lambda_{ii}\end{aligned}\ \ ,\ \ |A|=\begin{aligned}\prod_{i=1}^{n}\lambda_{ii}\end{aligned}\\$

相似变换

矩阵A经过对角化后得到对角阵B,则称AB相似,即A~B,
B= $P^{-1}AP$ ,相似矩阵间具有特征值矩阵与原矩阵到关系
可对角化条件:列向量个数=特征值个数,重根条件下，多少重根就多少个特征向量
实对称矩阵一定可对角化

二次型

定义

$f(x_1,x_2,..,x_n)=a_{11}x_1^2+a_{22}x_2^2+...+a_{nn}x_n^2+\begin{aligned}\sum_{j=1}^{n}\sum_{i=1}^{n}a_{ij} x_ix_j\end{aligned}\\$
矩阵表示
$\begin{pmatrix} a_{11}&\frac{a_{12}}{2}&&\\ \frac{a_{21}}{2}&a_{22}&&\\ &&...&\\ &&&a_{nn} \end{pmatrix}\\$

合同变换(Contract transformation)

矩阵A可分解为: $A=C^TBC$

合同矩阵:
1.原矩阵A为实对称矩阵
2.二次型的秩=未知数个数

化二次型的标准型

1.正交变换:系数矩阵 $A\xrightarrow[]{Contract transformation}$ 对角阵 $\rightarrow$ 将对角阵的元素作为y=cx的y系数 $\rightarrow$ 解出合同变换中的C(C的解要求基底正交规范化)(此处标准型就结束，若要规范型则继续) $\xrightarrow[Take\ the\ sign\ of\ B]{Normalize\ the\ vectors\ in\ P}$ 取y=cz作为规范型

2.配方法：利用完全平方进行配方

惯性定律

正惯性系数=矩阵的秩-负惯性系数=A中正特征向量的个数
正定二次型定义: $\forall X,we\ havef(X)>0\\$
正定矩阵:对应的二次型值>0 $\leftrightarrow$ 顺序主子式的值>0 $\leftrightarrow$ 正惯性系数p=未知数个数 $n\leftrightarrow$ 特征值均>0
半正定矩阵:正定矩阵中的条件”>”改为” $\geq$ ”
负定矩阵(应用霍尔维茨定理):顺序主子式呈现负正负正…的顺序排列

思维导图

提取码:cw1r

文章出处登录后可见！

已经登录？立即刷新

线性代数总复习(持续更新)

前言

矩阵

定义

运算