摘要

模拟退火算法来（SA）源于固体退火原理，是一种基于概率的算法，将固体加温至充分高，再让其徐徐冷却，加温时，固体内部粒子随温升变为无序状，内能增大，而徐徐冷却时粒子渐趋有序，在每个温度都达到平衡态，最后在常温时达到基态，内能减为最小。实验结果表明，SA 算法在处理 TSP 问题时，该算法具有较高的精度及较低的时间复杂度。

关键词:SA;TSP;解空间;评价函数;随机搜索

引言

TSP 问题（Traveling Salesman Problem）又译为旅行推销员问题、货郎担问题，是数学领域中著名问题之一。假设有一个旅行商人要拜访 n 个城市，他必须选择所要走的路径，路径的限制是每个城市只能拜访一次，而且最后要回到原来出发的城市。路径的选择目标是要求得的路径路程为所有路径之中的最小值。该问题是一个组合优化问题。该问题可以被证明具有 NPC 计算复杂性。因此，任何能使该问题的求解得以简化的方法，都将受到高度的评价和关注。迄今为止，这类问题中没有一个找到有效算法。倾向于接受 NP 完全问题（NP-Complete 或 NPC）和 NP 难题（NP-Hard 或 NPH）不存在有效算法这一猜想，认为这类问题的大型实例不能用精确算法求解，必须寻求这类问题的有效的近似算法。此类问题中，经典的还有子集和问题；Hamilton 回路问题；最大团问题。

为此，我们尝试使用模拟退火算法解决这类问题，利用物理退火达到平衡态时的统计思想，建立数学模型，编写该算法的 Python 程序，进行求解，得出最短旅行的最短距离；

正文

模拟退火算法基本思想

模拟退火是启发示算法的一种，也是一种贪心算法，但是它的搜索过程引入了随机因素。在迭代更新可行解时，以一定的概率来接受一个比当前解要差的解，因此有可能会跳出这个局部的最优解，达到全局的最优解。以下图为例，假定初始解为左边蓝色点 A，模拟退火算法会快速搜索到局部最优解 B，但在搜索到局部最优解后，不是就此结束，而是会以一定的概率接受到左边的移动。也许经过几次这样的不是局部最优的移动后会到达全局最优点 D，于是就跳出了局部最小值。

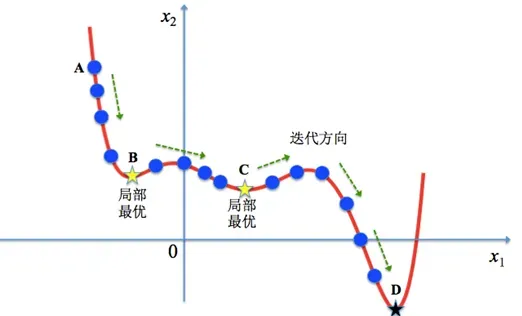
如图，D 为全局最优

模拟退火算法的基本流程

随机生成一个解 A,计算解 A 对应的目标函数值 f(A)

在 A 附近随机生成一个解 B，计算解 B 对应的目标函数值 f(B)

如果 f(B)>f(A)，则将解 B 赋值给解 A，然后重复上面步骤（爬山法的思想);。

如果 f(B)≤f(A)，那么计算接受 B 的概率

，然后生成一个[0.1]之间的随机数 r,如果 r<p,我们就将解 B 赋值给解 A,然后重复上面的步骤;否则我们返回第(2)步，在原来的 A 附近再重新生成一个解 B，然后继续下去。

的设置

定义初始温度

，温度下降的公式为:

，

常取 0.95，那么时刻 t 时的温度=100*0.95^t

取

,那么

注意:这里取倒数是为了保证 C 关于 t 递增。

在编程中的实现

t可以看成我们迭代的次数(循环)。为了保证搜索过程的彻底，在同一温度下(同一个小t)我们需要进行多次搜索（例如重复上面的流程500次);之后我们降低温度，然后再来进行新的一轮搜索。

模拟退火算法的优缺点

模拟退火算法的应用很广泛，可以高效地求解 NP 完全问题，如货郎担问题(Travelling Salesman Problem，简记为 TSP)、最大截问题(Max Cut Problem)、0-1 背包问题(Zero One Knapsack Problem)、图着色问题(Graph Colouring Problem)等等，但其参数难以控制，不能保证一次就收敛到最优值，一般需要多次尝试才能获得（大部分情况下还是会陷入局部最优值）。观察模拟退火算法的过程，发现其主要存在如下三个参数问题：

温度 T 的初始值设置问题

温度 T 的初始值设置是影响模拟退火算法全局搜索性能的重要因素之一、初始温度高，则搜索到全局最优解的可能性大，但因此要花费大量的计算时间；反之，则可节约计算时间，但全局搜索性能可能受到影响。

退火速度问题，即每个 T 值的迭代次数

模拟退火算法的全局搜索性能也与退火速度密切相关。一般来说，同一温度下的“充分”搜索是相当必要的，但这也需要计算时间。循环次数增加必定带来计算开销的增大。

温度管理问题

温度管理问题也是模拟退火算法难以处理的问题之一。实际应用中，由于必须考虑计算复杂度的切实可行性等问题。

完整的模拟退火算法流程图

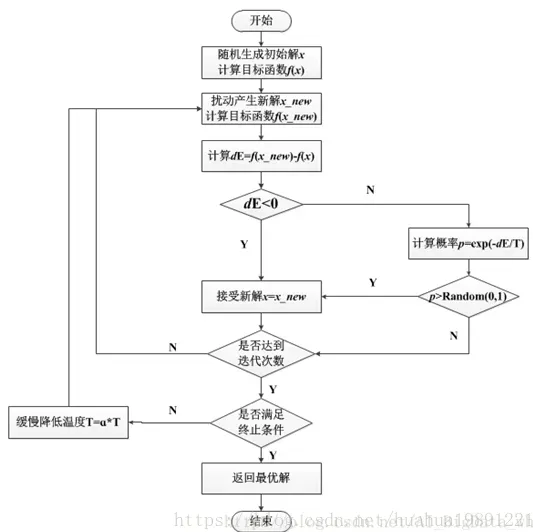
实验

实验使用一台 CPU 为 i7-8750H CPU @ 2.20GHz，内存为 8 GB 的电脑，算法使用 Python 实现。为便于实验，实验所用数据使用了直接在图片上标记点，然后提取标记点的坐标作为实验原始数据，最后以绘图的形式展示出初始的随机结果、SA 后的结果、迭代曲线以及在图像中呈现的最终结果。

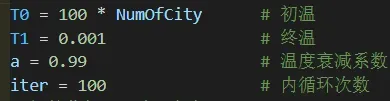
所采用的实验参数

City=15 时的实验结果

City=30 时的实验结果

结论

可以看出，本文算法在此试验参数下可以取得较高的精度。由于 City 数取值过高时算法耗时过大，故未将 City 值设置过大。在 City 数较小时，均能在迭代次数 4000~6000 次时找到最优解。在时间复杂度、空间复杂度和精确度属于较成功的解 TSP 算法。

参考文献

胡运权,运筹学基础及应用 (第六版)[M].2004.

姚新,陈国良,模拟退火算法及其应用[J].计算机研究与发展,1990(7):1-6.

Behzad, Arash;
Modarres, Mohammad, New Efficient Transformation of the Generalized Traveling Salesman Problem into Traveling Salesman Problem, Proceedings of the 15th International Conference of Systems Engineering (Las Vegas), 2002
Steinbrunn M,Moerkotte G, Kemper A. Heuristic and Randomized Optimization for the Join Ordering Problem[J ] . The VLDB Journal, 1997, 6 (3) :8 - 17.

卓金武.MATLAB 在数学建模中的应用—模拟退火算法[J].北京航空航天大学出版社，2014.9.
Join Ordering Problem[J ] . The VLDB Journal, 1997, 6 (3) :8 – 17.

卓金武.MATLAB 在数学建模中的应用—模拟退火算法[J].北京航空航天大学出版社，2014.9.