原文链接：CSDN-脉冲神经网络（SNN）论文阅读（三）—–高精度低时延的ANN转换SNN方法

目录

说明

准备将自己读的一些和SNN（脉冲神经网络）相关的一些论文记录下来，方便自己以后回看也希望能够帮到有需要的人。
删除了文中一些自认为不重要的内容而用自己的话进行简洁描述（很少，比如引言的一些内容），其他部分尽量使用专业用语进行翻译，如果有什么出错或不恰当的地方希望各位批评指出。

相关信息

论文地址: Optimal ANN-SNN Conversion for High-accuracy and Ultra-low-latency Spiking Neural Networks
论文由北京大学（于肇飞组）研究人员发表于ICLR 2022，代码发布于here

主要贡献

论文首先分析了ANN转SNN过程中的一些转换误差，然后提出了quantization clip-floor-shift activation function去替换ANN中的ReLU激活函数，这样转换后的SNN能够在较低的time step内达到较高的精度。

ANN转SNN相关公式以及动机

• 符号定义：首先，定义表示ANN中第层中所有神经元的输出，令表示在t时刻(时)脉冲神经元接收到前一层的输入后但并未发放脉冲前的膜电势，令表示在t时刻(时)脉冲神经元接收到前一层的输入并发放脉冲后的膜电势。
• 令表示脉冲神经元的放电阈值，表示在时刻第层中所有脉冲神经元发放的脉冲，假设神经元放电后传出的脉冲大小等于阈值，令表示第层的神经元向下一层传递的脉冲信息,表示第层神经元和第层神经元之间的权值。
• ANN转SNN：在ANN中有
  
  ，其中表示ReLU激活函数。在SNN中有
  
  通过将等式2从time step1累加到T，可以得到：
  
  使用表示从时刻0到T内的平均突触后电势，可以得到：
  
  等式4描述了相邻层之间脉冲神经元的平均突触后电势（）的关系。由于，如果让初始膜电势并且忽略掉，当令T（time step）足够大时等式4就几乎等同于等式1，即此时的SNN公式和ANN公式相等。然而太大的time step会导致很高的推理时间，从而影响SNN的实际应用，因此本文旨在在极低的延迟(time step)下实现高性能的ANN转换SNN。

转换误差分析

本部分详细分析ANN转换SNN中每一层存在的一些误差，此时假设ANN和SNN从前一层接收到的输入相等，即假设，然后开始分析第层存在的误差。

• 为了简化后续公式，使用表示第层传递至层的输入（ANN和SNN均如此）。
• 绝对转换误差 = 转换后的SNN的输出减去原始ANN的输出：
  
  从等式5中可以看到如果且则转化误差就不为0。事实上，转换误差由以下三个因素造成：

1. Clipping error：
   由于脉冲神经元的阈值为，所以SNN的输出，但是ANN的输出，其中表示的最大值。如图1a所示，可以通过下式映射到：
   
   这里的函数表示当时结果为a，时结果为b,时结果为x，表示向下取整，表示将映射为的的值。在ANN中的位于和之间的激活值都被映射为SNN中的，这样造成的转换误差称为clipping error。
   
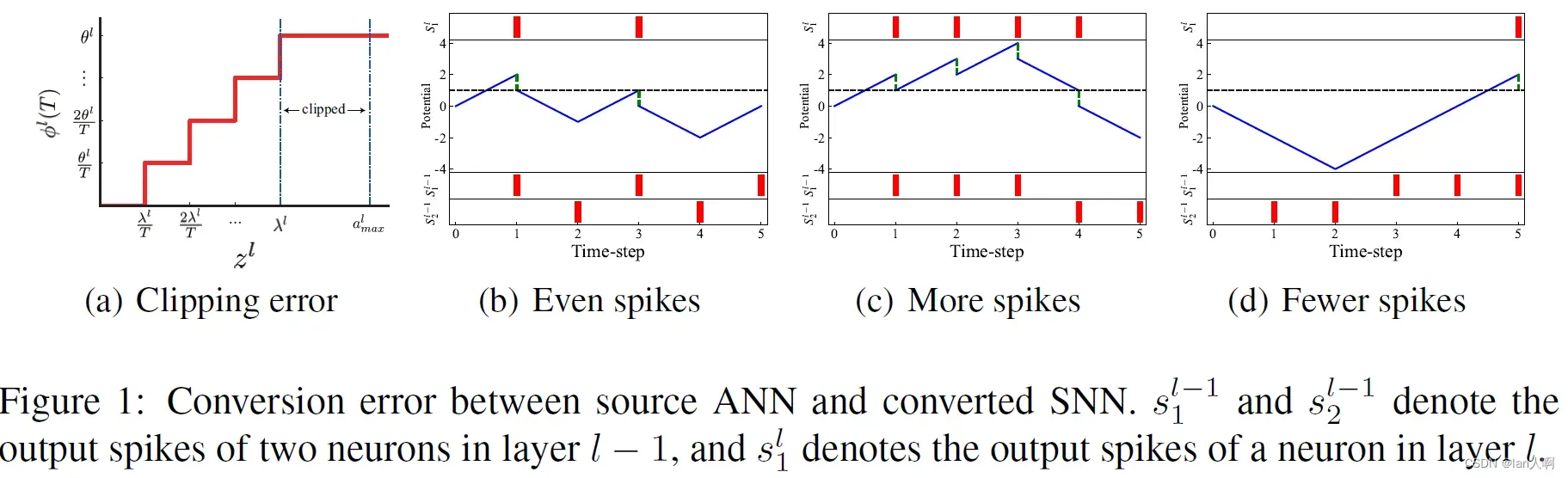
2. Quantization error（flooring error）：
   输出脉冲是离散事件，因此在经过量化后也是离散的，当把映射为时，不可避免地存在着一些量化误差。例如图1a中所示，ANN中位于之间的激活值在SNN中都被映射为。
3. Unevenness error：
   不均匀误差是由于输入脉冲的不均匀造成的。同样的脉冲数量，如果脉冲到达的时间不一样，产生的输出也不一样，可能会产生比预期更多或更少的输出。
   举个例子：
   假设在源ANN中第层中的两个神经元和第层一个神经元的连接权值分别是2和-2，第层两个神经元的输出是[0.6, 0.4]。在转换后的SNN中假设层的两个脉冲神经元在5个time step内(time step=5)分别发放3个脉冲和2个脉冲，令阈值。因此有。即使且ANN和SNN中的权值相等也会随着脉冲到达的时间不同而变化。ANN中的，对于SNN有如图1b-d所示的三种情况。
   如果两个权值为2和-2的神经元发放脉冲时间分别为和，突触后神经元将会在时刻发放脉冲，且。然而如果两个神经元发放脉冲时间分别为和，突触后神经元将会在时刻发放四个脉冲且;如果两个神经元发放脉冲时间分别为和，突触后神经元将只会在时刻发放一个脉冲且。

上述三种误差中存在一些相互依赖关系，特别是如果，不均匀误差会退化为量化误差，因此假设时可以忽略掉不均匀误差的影响从而估计SNN的激活函数。在转换后的SNN中估计输出值可以使用和函数来表示：

详细推导过程在论文的附录中，感兴趣的朋友可以去查看原始论文。
根据等式7，estimated conversion error 可以由下式得出：

优化的ANN转换SNN

quantization clip-floor activation function

由等式8可以得出，如果将ANN中的ReLU函数替换为带有一定量化步长L的clip-floor函数是不是能够消除掉在time step T=L时刻的转换误差呢？从而能够解决掉低时延的性能退化问题。
由上述思路，论文作者提出了quantization clip-floor activation function去训练ANN：

其中的超参数表示ANN中的量化步长（quantization step），而是可训练的参数，决定着将ANN中映射到SNN中的最大值对应的最大值（比较绕，其实说白了就是）。使用这样一个新的激活函数，满足以下几个条件时ANN和转换后的SNN之间的转换误差为0：

• 条件：量化步长L=time step T；；
• 缺陷：在时误差不一定为0。

进一步改进的quantization clip-floor-shift activation function

基于以上缺陷，论文作者又提出了进一步改进的quantization clip-floor-shift activation function：

和式9相比，式10多了一个超参数向量来控制激活函数的偏移（shift）。当时虽然不能保证转换误差为0，但是可以估计转换误差的期望值。相似于Deng & Gu, 2020¹，这里同样假设服从一定的均匀分布，当满足以下条件时，可以证明当源ANN中的时对于任意的T和L，转换误差的期望值接近于0。

• 条件：；。
  证明过程在论文附录中给出，感兴趣的朋友可以去查看原始论文。
  结果表示当时即使平均转换误差也接近于0，从而能够在极低的time step内实现高性能的转换后的SNN。

用于带有quantization clip-floor-shift activation function的训练算法

训练带有quantization clip-floor-shift activation function的ANN也是一个问题。在训练时，论文作者采用straight-through estimatorBengio et al., 2013²作为floor函数的导数，即令。整体的导数规则如下式17所示：

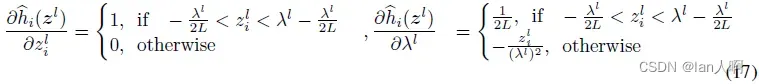
实验部分

作者使用VGG-16、ResNet-18、ResNet-20等网络结构在CIFAR-10、CIFAR-100和ImageNet数据集上做了实验证明了该方法的优越性。另外表示随着L的增加，转换后的SNN在time step较小时的精度也会随之下降，即L过大过小都不行，推荐的L为4或8.

部分参考文献

本文由CSDN-lan人啊原创，转载请注明！