原文标题 :Tune Deep Neural Networks using Bayesian Optimization
使用贝叶斯优化调整深度神经网络
利用贝叶斯理论来提高你的表现

在上一篇文章中,我们介绍了一个关于使用 TensorFlow 和深度学习方法进行图像分类的案例研究。[0]
尽管案例研究很少,但它展示了机器学习项目的每个阶段:清理、预处理、模型构建、训练和评估。但是我们跳过了调优。
在本文中,我们将深入研究超参数优化。同样,我们将使用 Tensorflow 中包含的 Fashion MNIST[1] 数据集。[0]
提醒一下,该数据集在训练集中包含 60,000 张灰度图像,在测试集中包含 10,000 张图像。每张图片代表属于 10 个类别之一的时尚单品(“T 恤/上衣”、“裤子”、“套头衫”等)。因此,我们有一个多类分类问题。
Setup
我将简要介绍准备数据集的步骤。更多信息请查看上一篇文章的第一部分:简而言之,步骤是:[0]
- Load the data.
- 分为训练集、验证集和测试集。
- 将像素值从 0–255 标准化到 0–1 范围。
- One-hot 编码目标变量。
回顾一下,所有训练、验证和测试集的形状是:
Hyperparameter tuning
现在,我们将使用 Keras Tuner 库 [2]:它将帮助我们轻松调整神经网络的超参数。要安装它,请执行:
pip install keras-tuner注意:Keras Tuner 需要 Python 3.6+ 和 TensorFlow 2.0+
快速提醒一下,超参数调整是机器学习项目的基础部分。有两种类型的超参数:
- 结构超参数:定义模型的整体架构(例如隐藏单元的数量、层数)
- 优化器超参数:影响训练速度和质量的参数(例如学习率和优化器类型、批量大小、时期数)
为什么调音很棘手?
为什么需要超参数调优库?我们不能尝试所有可能的组合,看看验证集上什么是最好的吗?
Unfortunately, no:
- 深度神经网络需要大量时间来训练,甚至几天。
- 如果您在云上训练大型模型(例如 Amazon Sagemaker),请记住每个实验都需要花钱。
因此,需要一种限制超参数搜索空间的剪枝策略。
Bayesian optimization
幸运的是,Keras 调谐器提供了贝叶斯优化调谐器。贝叶斯优化调谐器不是搜索每个可能的组合,而是遵循一个迭代过程,它随机选择前几个。然后,根据这些超参数的性能,贝叶斯调谐器选择下一个可能的最佳值。
因此,每个超参数的选择都取决于之前的尝试。根据历史记录选择下一组超参数并评估性能的迭代次数将继续,直到调谐器找到最佳组合或用尽最大试验次数。我们可以使用参数“max_trials”来配置它。
除了贝叶斯优化调谐器之外,Keras 调谐器还提供了另外两个调谐器:RandomSearch 和 Hyperband。我们将在本文末尾讨论它们。
回到我们的例子
接下来,我们将对我们的网络应用超参数调整。在上一篇文章中,我们尝试了两种网络架构,标准多层感知器(MLP)和卷积神经网络(CNN)。
Multilayered Perceptron (MLP)
但首先,让我们记住我们的基线 MLP 模型是什么:
调优过程需要两种主要方法:
- hp.Int():设置超参数的范围,其值为整数 – 例如,密集层中隐藏单元的数量:
model.add(Dense(units = hp.Int('dense-bot', min_value=50, max_value=350, step=50))2. hp.Choice():为超参数提供一组值——例如,Adam 或 SGD 作为最佳优化器?
hp_optimizer=hp.Choice('Optimizer', values=['Adam', 'SGD'])因此,在我们原始的 MLP 示例中使用贝叶斯优化调谐器,我们测试了以下超参数:
- 隐藏层数:1-3
- 第一密集层大小:50–350
- 第二和第三密集层大小:50–350
- Dropout Rate: 0, 0.1, 0.2
- 优化器:SGD(nesterov=True,momentum=0.9) 或 Adam
- Learning Rates: 0.1, 0.01, 0.001
注意第 5 行的 for 循环:我们让模型决定网络的深度!
最后,我们启动调谐器。请注意我们之前提到的 max_trials 参数。
This will print:
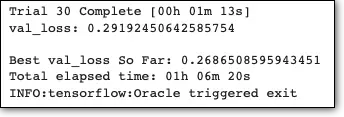
该过程用尽了迭代次数,大约需要 1 小时才能完成。我们还可以使用以下命令打印模型的最佳超参数:

就是这样!我们现在可以使用最优超参数重新训练我们的模型:
或者,我们可以用更少的冗长重新训练我们的模型:
我们现在要做的就是检查测试的准确性:
# Test accuracy: 0.8823与基线的模型测试精度相比:
Baseline MLP model: 86.6 %
Best MLP model: 88.2 %
事实上,我们观察到测试准确度的差异约为 3%!
卷积神经网络 (CNN)
同样,我们将遵循相同的程序。使用 CNN,我们可以测试更多参数。
首先,这是我们的基线模型:
基线模型仅包含一组过滤和池化层。对于我们的调优,我们将测试以下内容:
- 卷积、MaxPooling 和 Dropout 层的“块”数
- 每个块中 Conv 层的过滤器大小:32、64
- 转换层上的有效或相同填充
- 最后一个额外层的隐藏层大小:25-150,乘以 25
- 优化器:SGD(nesterov=True,动量=0.9)或 Adam
- Learning Rates: 0.01, 0.001
model = Sequential()
model = Sequential()
model.add(Input(shape=(28, 28, 1)))
for i in range(hp.Int('num_blocks', 1, 2)):
hp_padding=hp.Choice('padding_'+ str(i), values=['valid', 'same'])
hp_filters=hp.Choice('filters_'+ str(i), values=[32, 64])
model.add(Conv2D(hp_filters, (3, 3), padding=hp_padding, activation='relu', kernel_initializer='he_uniform', input_shape=(28, 28, 1)))
model.add(MaxPooling2D((2, 2)))
model.add(Dropout(hp.Choice('dropout_'+ str(i), values=[0.0, 0.1, 0.2])))
model.add(Flatten())
hp_units = hp.Int('units', min_value=25, max_value=150, step=25)
model.add(Dense(hp_units, activation='relu', kernel_initializer='he_uniform'))
model.add(Dense(10,activation="softmax"))
hp_learning_rate = hp.Choice('learning_rate', values=[1e-2, 1e-3])
hp_optimizer=hp.Choice('Optimizer', values=['Adam', 'SGD'])
if hp_optimizer == 'Adam':
hp_learning_rate = hp.Choice('learning_rate', values=[1e-2, 1e-3])
elif hp_optimizer == 'SGD':
hp_learning_rate = hp.Choice('learning_rate', values=[1e-2, 1e-3])
nesterov=True
momentum=0.9像以前一样,我们让网络决定它的深度。
现在,我们准备调用贝叶斯调谐器。最大迭代次数设置为 100:
model.compile( optimizer=hp_optimizer,loss='categorical_crossentropy', metrics=['accuracy'])
tuner_cnn = kt.tuners.BayesianOptimization(
model,
objective='val_loss',
max_trials=100,
directory='.',
project_name='tuning-cnn')This will print:
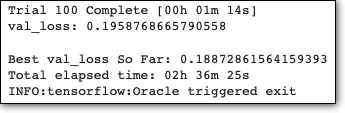
最好的超参数是:
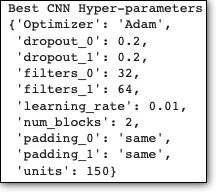
最后,我们使用最佳超参数训练我们的 CNN 模型:
model_cnn = Sequential()
model_cnn.add(Input(shape=(28, 28, 1)))
for i in range(best_cnn_hyperparameters['num_blocks']):
hp_padding=best_cnn_hyperparameters['padding_'+ str(i)]
hp_filters=best_cnn_hyperparameters['filters_'+ str(i)]
model_cnn.add(Conv2D(hp_filters, (3, 3), padding=hp_padding, activation='relu', kernel_initializer='he_uniform', input_shape=(28, 28, 1)))
model_cnn.add(MaxPooling2D((2, 2)))
model_cnn.add(Dropout(best_cnn_hyperparameters['dropout_'+ str(i)]))
model_cnn.add(Flatten())
model_cnn.add(Dense(best_cnn_hyperparameters['units'], activation='relu', kernel_initializer='he_uniform'))
model_cnn.add(Dense(10,activation="softmax"))
model_cnn.compile(optimizer=best_cnn_hyperparameters['Optimizer'],
loss='categorical_crossentropy',
metrics=['accuracy'])
print(model_cnn.summary())
history_cnn= model_cnn.fit(train_x, train_y, epochs=50, batch_size=32, validation_data=(dev_x, dev_y), callbacks=callback)并检查测试集的准确性:
cnn_test_loss, cnn_test_acc = model_cnn.evaluate(test_x, test_y, verbose=2)
print('\nTest accuracy:', cnn_test_acc)# Test accuracy: 0.92与基线的 CNN 模型测试精度相比(来自我们之前的文章):
Baseline CNN model: 90.8 %
Best CNN model: 92%
再次,我们看到优化模型的性能提升!
除了准确性之外,我们可以确认调谐器做得很好,原因如下:
- 调谐器在每种情况下都选择了一个非零的 Dropout 值,即使我们也为调谐器提供了零 Dropout。这是意料之中的,因为 Dropout 是一种减少过拟合的宝贵机制。
- 有趣的是,最好的 CNN 架构是标准管道,其中过滤器的数量在每一层中逐渐增加。这是意料之中的,因为随着后续层的计算向前推进,模式变得更加复杂。因此,有更多的模式组合需要更多的过滤器才能被捕获。
Closing Remarks
毫无疑问,Keras Tuner 是使用 Tensorflow 优化深度神经网络的多功能工具。
最明显的选择是贝叶斯优化调谐器。但是,还有两个其他人可以使用的选项:
- RandomSearch:这种类型的调谐器通过随机选择其中的一些来避免探索超参数的整个搜索空间。但是,它不能保证此调谐器会找到最佳调谐器。
- Hyperband:此调谐器选择一些超参数的随机组合,并仅使用它们来训练模型几个 epoch。然后,调谐器使用这些超参数来训练模型,直到用尽所有 epoch 并从中选择最好的。
感谢您的阅读!
References
- Zalando 的时尚 MNIST 数据集,https://www.kaggle.com/datasets/zalando-research/fashionmnist,麻省理工学院许可证 (MIT) 版权所有 © [2017][0]
- Keras 调谐器,https://keras.io/keras_tuner/[0]
文章出处登录后可见!
