本文部分理论引用了:4 Strategies for Multi-Step Time Series Forecasting
Multivariate Time Series Forecasting with LSTMs in Keras (machinelearningmastery.com)
(更新于2022年10月,最近需要做相关的大型实验,对这个LSTM神经网络预测有了更深的认识,也发现以往有些概念是错误的,在这里记录一下。有问题或者有其他预测需求可以直接私聊我一起交流,我有空的时候会看的。)
(1.首先题目的“时序多步预测”改为了“时序预测”,其实这个代码算是一个多次的单步预测,而且并不需要一次性去预测两步(如果需要改的话,需要改神经网络预测中的交替时间步,可以用一个XTrain对应两个YTrain中的两个数,那就可以多步预测了。原理和结果详情可见置顶的第二篇文章,里面基于Python提到了一次性预测两步的问题),因为LSTM不断在更新网络,所以这样反而精度下降了。但是那个在前文提到,交替一个时间步的预测效果是最好的,因为很显然,只预测一步当然比预测两步的效果好。)
(2.在文章中区分出lag和多步预测(预测步数为a)的概念。这个概念在之前有些混淆。lag指的是利用当前数据去预测下一个数据时中间隔了多少秒。预测步数a指的是利用当前数据去预测下一几个时间步的数据。)
(网上资料繁杂众多,而且到底如何预测也没有一个准确答案,基本都是教如何训练神经网络以及验证神经网络的准确度的,但是都没有一个神经网络的实战,本文将好好记录一下我这些年的所思所感以及LSTM神经网络在实验中的应用,所用源代码+数据(非实验所用,经过简化处理)将会以文件的方式供大家下载,有需要的自己去下载使用。希望能给大家启发。)
LSTM时序预测神经网络与NAR、NARx等时序预测神经网络结构有着本质上的不同,像其他几篇博客所述,通过观察工作区发现,NAR和NARx的输入实际上是“延迟向量”。LSTM神经网络因为“门”这种特殊的概念引入,使其有着更长、更好的时间预测效果。 本文将根据LSTM有两种预测方式,一种是根据预测值去更新网络状态,另外一种是根据观测值去更新网络状态。
目录
Step2:构造交替5秒时间间隔的时间序列作为神经网络的输入和输出。
一、根据预测值去更新网络状态(单序列数据用)
数据集、源码地址:(直接运行就能用)
放在评论区了,放在文字里面没法通过审核。
实现的是:已知前面几年的数据,往后预测2023年的100天的数据。
Step1:加载数据,并进行数据预处理
clc
clear
load dataset.mat %加载数据(double型,剔除了2023年的的第一个数据,总共为2191个。时序预测没有实际时间,只有事情发生的顺序)
data=data(:,2)'; %不转置的话,无法训练lstm网络,显示维度不对。
%% 序列的前2000个用于训练,后191个用于验证神经网络,然后往后预测200个数据。
dataTrain = data(1:2000); %定义训练集
dataTest = data(2001:2191); %该数据是用来在最后与预测值进行对比的
%% 数据预处理
mu = mean(dataTrain); %求均值
sig = std(dataTrain); %求均差
dataTrainStandardized = (dataTrain - mu) / sig; LSTM对于数据标准化要求很高。且这里只对训练集进行标准化的原因是经过神经网络中的值只有训练集,因此无须对测试集进行标准化。
Step2:交替一个时间步
%% 输入的每个时间步,LSTM网络学习预测下一个时间步,这里交错一个时间步效果最好。
XTrain = dataTrainStandardized(1:end-1);
YTrain = dataTrainStandardized(2:end); 大多数LSTM相关的资料还是使用默认的a=1来将时间序列拆分为具有输入和输出分量的样本。我在自己的其他试验中使用不同的a来观察(a=1,2,5,10)。这个a的意思是规定了一次性往后预测多少步。设置不同的预测步数a的目的是观察是否能够改善预测模型性能。但据某些验证表明,增加滞后并不能改善预测模型的性能。其实也很好理解,单次预测精度肯定是比预测两步的精度要高的。
a=1即输入[[1],[2],[3],…,[10]]对应着输出[[2],[3],[4],…[11]],a为2的时候即[[1],[2],[3],…,[10]]对应着[[2,3],[3,4],[4,5],…,[10,11]。
这里的交替时间步的作用是什么呢?
- 转化序列数据使其呈静态。具体来说,就是使用 a=1差分移除数据中的增长趋势。
- 将时间序列问题转化为监督学习问题。具体来说,就是将数据组为输入和输出模式,上一时间步长的观察值可作为输入用于预测当前时间步长的观察值。
Step3:定义LSTM网络架构并训练
%% 一维特征lstm网络训练
numFeatures = 1; %特征为一维
numResponses = 1; %输出也是一维
numHiddenUnits = 200; %创建LSTM回归网络,指定LSTM层的隐含单元个数200。可调
layers = [ ...
sequenceInputLayer(numFeatures) %输入层
lstmLayer(numHiddenUnits) % lstm层,如果是构建多层的LSTM模型,可以修改。
fullyConnectedLayer(numResponses) %为全连接层,是输出的维数。
regressionLayer]; %其计算回归问题的半均方误差模块 。即说明这不是在进行分类问题。
%指定训练选项,求解器设置为adam, 1000轮训练。
%梯度阈值设置为 1。指定初始学习率 0.01,在 125 轮训练后通过乘以因子 0.2 来降低学习率。
options = trainingOptions('adam', ...
'MaxEpochs',1000, ...
'GradientThreshold',1, ...
'InitialLearnRate',0.01, ...
'LearnRateSchedule','piecewise', ...%每当经过一定数量的时期时,学习率就会乘以一个系数。
'LearnRateDropPeriod',400, ... %乘法之间的纪元数由“ LearnRateDropPeriod”控制。可调
'LearnRateDropFactor',0.15, ... %乘法因子由参“ LearnRateDropFactor”控制,可调
'Verbose',0, ... %如果将其设置为true,则有关训练进度的信息将被打印到命令窗口中。默认值为true。
'Plots','training-progress'); %构建曲线图 将'training-progress'替换为none
net = trainNetwork(XTrain,YTrain,layers,options); 需要提醒的是:在MATLAB中,其已经将LSTM网络进行封装,类似工具箱的形式,因此不再涉及底层的“门”概念。如果利用Python去编程,将会涉及到。
这里有三个参数很重要,第一个是numHiddenUnits,第二是LearnRateDropPeriod,第三个是LearnRateDropFactor,这三个需要根据你的数据集去改。如果RMSE曲线下降太慢,那么就可能是以下原因:(在本代码中,需要将LearnRateDropPeriod改大。)

Step4:初始化网络状态
net = predictAndUpdateState(net,XTrain); %将新的XTrain数据用在网络上进行初始化网络状态
[net,YPred] = predictAndUpdateState(net,YTrain(end)); %用训练的最后一步来进行预测第一个预测值,给定一个初始值。这是用预测值更新网络状态特有的。训练的最后一个,即预测的第一个。
Step5:利用LSTM网络进行单步预测
%% 进行用于验证神经网络的数据预测(用预测值更新网络状态)
for i = 2:291 %从第二步开始,这里进行191次单步预测(191为用于验证的预测值,100为往后预测的值。一共291个)
[net,YPred(:,i)] = predictAndUpdateState(net,YPred(:,i-1),'ExecutionEnvironment','cpu'); %predictAndUpdateState函数是一次预测一个值并更新网络状态
end在其他博客提到的NAR和NARx中,递归预测会一直累积误差,以至于使性能迅速下降,但LSTM对比其他网络独有的是其有这个特殊的函数predictAndUpdateState能够在每次预测时更新网络状态,因此其能够预测更长的序列。
Step6:将预测结果与实际数据对比
%% 验证神经网络
YPred = sig*YPred + mu; %使用先前计算的参数对预测去标准化。
rmse = sqrt(mean((YPred(1:191)-dataTest).^2)) ; %计算均方根误差 (RMSE)。
subplot(2,1,1)
plot(dataTrain(1:end)) %先画出前面2000个数据,是训练数据。
hold on
idx = 2001:(2000+191); %为横坐标
plot(idx,YPred(1:191),'.-') %显示预测值
hold off
xlabel("Time")
ylabel("Case")
title("Forecast")
legend(["Observed" "Forecast"])
subplot(2,1,2)
plot(data)
xlabel("Time")
ylabel("Case")
title("Dataset")
%% 继续往后预测2023年的数据
figure(2)
idx = 2001:(2000+291); %为横坐标
plot(idx,YPred(1:291),'.-') %显示预测值
hold offStep7:重置网络状态
net = resetState(net); 如果需要进行其他的预测,如进行下一轮300个的预测。需要重置一下网络状态。
训练结果: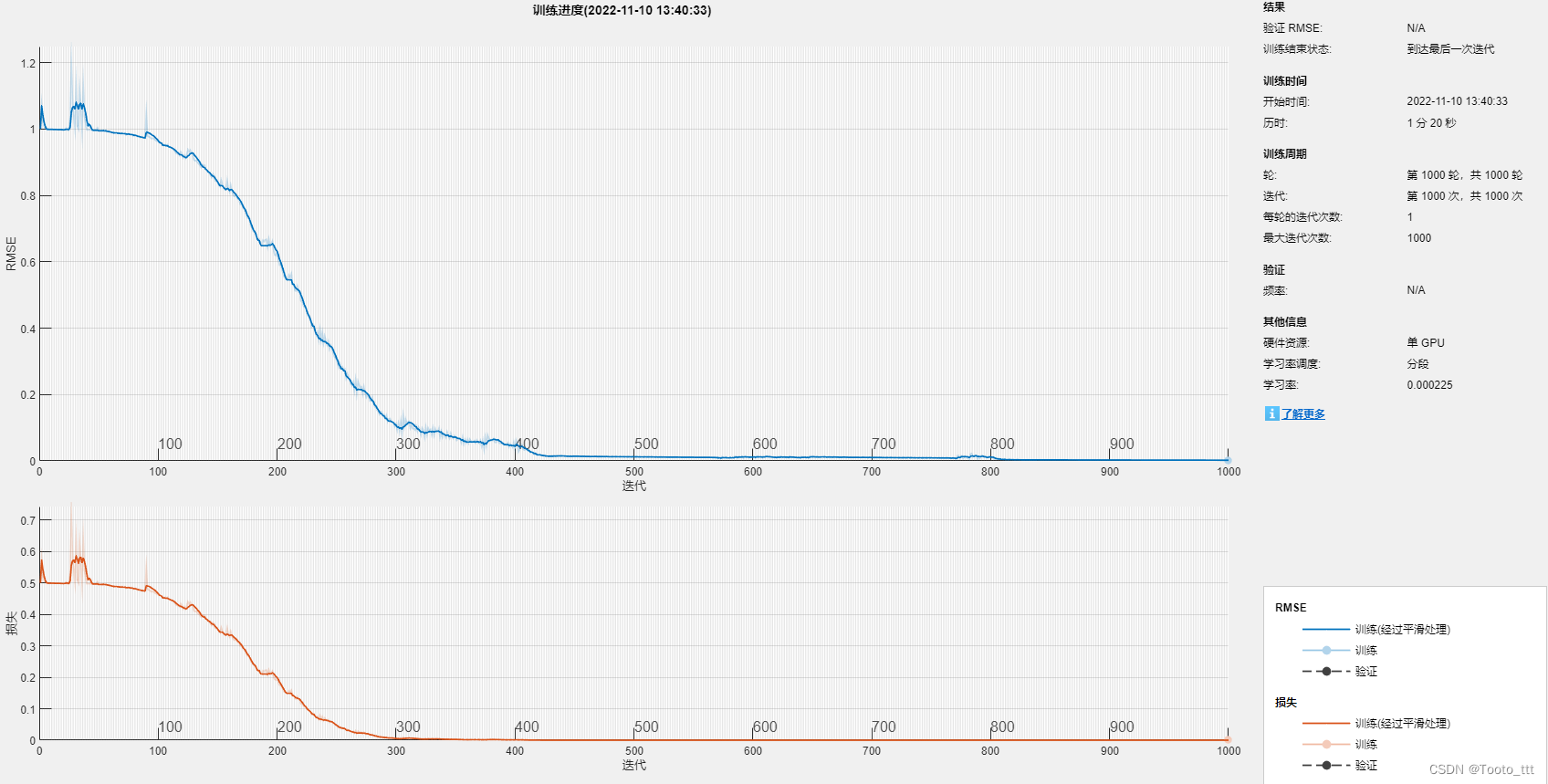
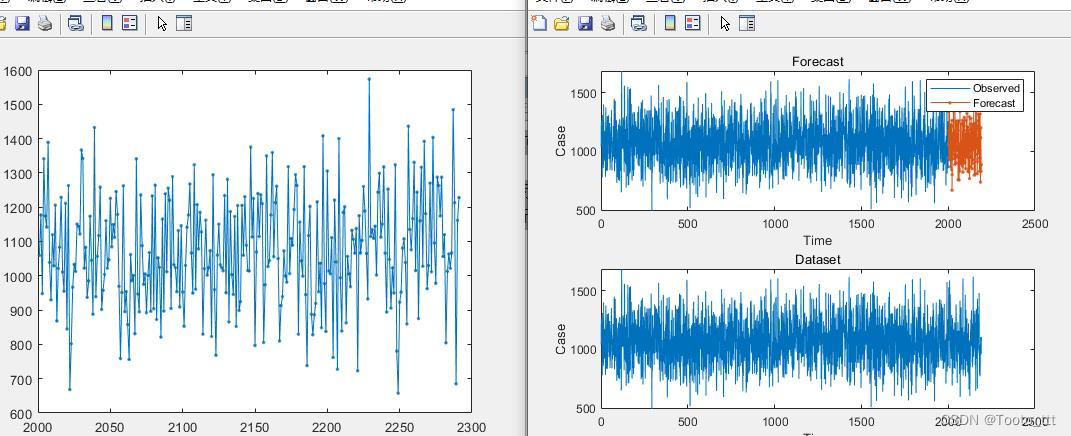
左图表示的是,从2191个开始,往后预测了100个。右图表示的是利用2001:2191个数据来验证神经网络的训练结果,这里还是比较好的。
但在预测的时候,不能单从训练集和预测集的数量以及比例去评价这个数据集的好坏,从理论上来说,训练集应包含多个周期的变化,不然肯定无法通过此去进行预测。而且100个数据去预测30个数据这并不意味着用1000个数据去预测后面300个是一样的表现,两者是不相同的。
使预测模型更加精确的方法有:增加预测输入的维度,即加入不同的特征(如下文所提到的多个波高仪)。同时需要注意的是,该模型仅适用于单序列预测(即仅有波浪力这个数据,去预测后面的波浪力,因此其实它的预测精度也是不高的。)
二、根据观测值去更新网络状态(实验用、多序列)
在实验中的需求是:利用5个波高仪的波高数据去预测去一段时间间隔(5秒)后的波浪力。因此神经网络训练所需要的是足够数量的波高、波浪力数据样本,每一步将5个波高仪的数据去跟5秒后的波浪力数据进行对应即可。由于实验数据不能泄露,因此大家可参透代码根据自己的实际情况进行使用。
Step1:加载数据,并进行数据预处理
%% 将所有测得的数据切分为7500个数据和对数据进行标准化,消除变量之间的量纲关系,使数据具有可比性。
load testdata.mat %其中第一列为时间,第二列至第六列为波高数据,第七列为波浪力数据。
dt=0.01 %这里的每一步的间隔为0.01秒,可根据实际实验采样频率情况来定。
time_lag=500; %这里指的是根据波高力数据预测5秒后的波浪力,这个间距可以自己根据实际来调整。
N_total=7500; %这里指的是7500个时间步
t=testdata(:,1); %时间,共有7500个。
std_scale=std(testdata(:,2:7)); %对波高数据和波浪力数据求标准差
testdata_norm(:,2:7) =normalize(testdata(:,2:7)); %将数据归一化
lag=500;
Step2:构造交替5秒时间间隔的时间序列作为神经网络的输入和输出。
%% 首先先将时间步分割好
t_input=t(1:end-lag); %7000=7500-500。1:7000个
t_output=t(lag+1:end); %501:7500个
%% 分割波高数据和波浪力数据
height_input(1:5,:)=testdata_norm(1:end-lag,2:6)'; %因此这里height_input中的每一行是一个波高仪的数据,一共有5个波高仪,每个波高仪收集了1-7500个时间步的波高信息。然后这里波高作为输入,是只截取第1-7000个时间步的数据作为输入。
height_output(1,:)=testdata_norm(lag+1:end,7)'; %这里指的是第501~7500个时间步的波浪力作为输出。
%% 决定网络的输入、输出、总数
net_input=height_input; %1:7000,指代的是波高信息
net_output=height_output; %501:7500,指代的是波浪力信息
sample_size=length(height_output); %样本总数7000Step3:神经网络训练
%% 训练神经网络参数设定
numHiddenUnits =5; %指定LSTM层的隐含单元个数为5
train_ratio= 0.8; %划分用于神经网络训练的数据比例为总数的80%
LearnRateDropPeriod=50; %乘法之间的纪元数由“ LearnRateDropPeriod”控制
LearnRateDropFactor=0.5; %乘法因子由参“ LearnRateDropFactor”控制,
%% 定义训练时的时间步。
numTimeStepsTrain = floor(train_ratio*numel(net_input(1,:))); %一共为7000个*0.8=5600个
%% 交替一个时间步,可以交替多个时间步,但这里交替一个时间步的效果其实是最好的,详见那篇开头第二篇建立在python之上的文章。(真正想要改变往后预测时间的长短为lag这个变量。)
XTrain = net_input(:, 1: numTimeStepsTrain+1); %1~5601,XTrain---input,一共为5601个
YTrain = net_output(:, 2: numTimeStepsTrain+2); %2~5602,YTrain---expected output,为5601个
%% 输入有5个特征,输出有1个特征。
numFeatures = numel(net_input(:,1)); %5
numResponses = numel(net_output(:,1)); %1
layers = [ ...
sequenceInputLayer(numFeatures) %输入层为5
lstmLayer(numHiddenUnits) %lstm层,构建5层的LSTM模型,
fullyConnectedLayer(numResponses) %为全连接层,是输出的维数。
regressionLayer]; %其计算回归问题的半均方误差模块 。即说明这不是在进行分类问题。
options = trainingOptions('adam', ... %指定训练选项,求解器设置为adam, 1000轮训练。
'MaxEpochs',150, ... %最大训练周期为150
'GradientThreshold',1, ... %梯度阈值设置为 1
'InitialLearnRate',0.01, ... %指定初始学习率 0.01
'LearnRateSchedule','piecewise', ... %每当经过一定数量的时期时,学习率就会乘以一个系数。
'LearnRateDropPeriod', LearnRateDropPeriod, ...
'LearnRateDropFactor',LearnRateDropFactor, ... %在50轮训练后通过乘以因子 0.5 来降低学习率。
'Verbose',0, ... %如果将其设置为true,则有关训练进度的信息将被打印到命令窗口中,0即是不打印 。
'Plots','training-progress'); %构建曲线图 ,不想构造就将'training-progress'替换为none
net = trainNetwork(XTrain,YTrain,layers,options); %训练神经网络
save('LSTM_net', 'net'); %将net保存为LSTM_net
end
Step4:神经网络预测+精度反映
%% 定义Xtest和Ytest,其目的是仿照神经网络训练中XTrain和YTrain的样式去构造一个测试集
%% input_Test指的是实验中得到的波高数据。
%% output_Test指的就是参与跟预测值进行对比的测量值。即expected output
numTimeStepsTrain2 = floor(0.1*sample_size); %一共为7000个*0.1=700个。可以自己再随意取一个比例,去尝试一下。当然也可以跟上面的numTimeStepsTrain保持一致。
input_Test = net_input(:, numTimeStepsTrain2+1: end-1); %7000个中取701个~6999,一共是6299个
output_Test = net_output(:, numTimeStepsTrain2+2: end); %7000个取702:7000,为6299个,因为 numTimeStepsTrain是700.
%% 这里首先用input_Train来初始化神经网络。经过测试,不是将整个input_Train放进去最好,放其中一点比例即可。
input_Train = net_input(:, floor(numTimeStepsTrain*0.9): numTimeStepsTrain); %630~700
net = predictAndUpdateState(net, input_Train);
%% 预测量预定义
rec_step=numel(output_Test); %滚动预测6299个。跟后面的j循环有关。
YPred=zeros(rec_step,1); %6299个预测,1个特征。这个预测是和Test来比对,看是否正确的。
%% 神经网络预测(这个也是之后实际预测需要用到的)
for j=1: rec_step
[net,YPred0] = predictAndUpdateState(net, input_Test(:, j)); %用input_Test代入刚刚用input_Train来更新的网络得到第一个输出并得到对应的预测值。
YPred(j, :) = YPred0; %记录输出的预测值。
end
%% 神经网络精度反映。这里的Y都是波浪力
YTest = output_Test(:,1:rec_step)'; %这一步可以简化。其实只是一个转置。
NRMSE=sqrt(sum((YPred-YTest).^2)/rec_step/(max(YTest)-min(YTest)));这里需要重点说明的是用input_Train来初始化神经网络的问题。 因为在LSTM中,state cell是实时在更新的,但对于整个网络需要给它一个初始化的值,但不一定是利用整个input_Train的效果最好,因此在实际使用中input_Train可以考虑给予一个比例,来让其初始化。
Step5:神经网络实际应用
rec_step=2; %这里只预测两步
input_Test=[1;2;3;4;5,6;4;8;9;7]; %假设第一个时间步波高数据分别为1,2,3,4,5,第二个时间步波高数据分别为6;4;8;9;7。
%% 神经网络预测
for j=1: rec_step
[net,YPred0] = predictAndUpdateState(net, input_Test(:, j)); %用input_Test代入刚刚用input_Train来更新的网络得到第一个输出并得到对应的预测值。
YPred(j, :) = YPred0; %记录输出2个的预测值。
end
假设已经同时得到了5个波高仪数据,需要预测5秒(在之前的神经网络训练中已经预设好了)后的波浪力。每次得到的波高数据应该是放在for循环里面,去不断的进行单步预测。

左边是数据集,右边是预测,我在预测中的输入是2秒前的波高,预测了2秒后的波浪力。这个相当于多次的单步预测,还是相当的准确的。
文章出处登录后可见!
