🚀个人主页:欢迎访问Ali.s的首页
⏰ 最近更新:2022年8月18日
⛽ Java框架学习系列:【Spring】【SpringMVC】【Mybatis】
🔥 Java项目实战系列:【飞机大战】【图书管理系统】
🍭 Java算法21天系列:【查找】【排序】【递归】
⛳ Java基础学习系列:【继承】【封装】【多态】
🏆 通信仿真学习系列:【硬件】【通信】【MATLAB】
🍄 个人简介:通信工程本硕🌈、Java程序员🚴。目前只会CURD😂
💌 点赞 👍 收藏 💗留言 💬 都是我最大的动力💯


文章目录
前言
傅里叶变换和傅里叶级数是有史以来最伟大的数学发现之一。它们可以帮助我们将函数分解成其基本成分。它们揭示了任何数学函数的基本模块,但是傅里叶分析的公式对于连高数中sin2x的积分都不熟悉的工科白菜来说简直就是连多看它一样的勇气都没有,我想这就是为什么复杂的傅里叶分析成为大学中通信专业的疑难杂症的主要原因,更不要说学好《信号与系统》、《通信原理》这些专业课程了,所以本文就从不一样的角度来研究它的本质,来揭开傅里叶级数与傅里叶变换的神秘面纱。
一、时域与频域
以你来到这个世界为起点,随着时间的流逝,你将会在时间轴上留下属于你的时间烙印;股票的走势随着时间的变化而变化,在每个具体的时间点上都会有属于它的价格;这种以时间作为节点来看待问题的方法便是时域分析。
 这么看来,好像所有的事务都是随着时间不断的发展的,如果你有这种想法,那么恭喜你,你应该就是那个傅里叶学不好的白菜。其实从频域的角度看,这个世界便是静止的了,这里所说的静止不是你们学的那个哲学世界是变化的非静止的,要用变化的眼光看待问题的那个静止。下面用钢琴的音节来表示频域的特征,每个音节的组合,才弹奏出音乐,我们观察到钢琴的琴弦一会上一会下的摆动,就如同一支股票的走势,而在频域,只有那一个永恒的音节。
这么看来,好像所有的事务都是随着时间不断的发展的,如果你有这种想法,那么恭喜你,你应该就是那个傅里叶学不好的白菜。其实从频域的角度看,这个世界便是静止的了,这里所说的静止不是你们学的那个哲学世界是变化的非静止的,要用变化的眼光看待问题的那个静止。下面用钢琴的音节来表示频域的特征,每个音节的组合,才弹奏出音乐,我们观察到钢琴的琴弦一会上一会下的摆动,就如同一支股票的走势,而在频域,只有那一个永恒的音节。

二、傅里叶级数
1、傅里叶级数的理解
当你看到下面这个傅里叶级数的公式时,你肯定时一个头两个大,但一打开《信号与系统》、《通信原理》等书籍,动不动就跳出一个傅里叶级数或傅里叶变换,弄一长串公式,让人云山雾罩。
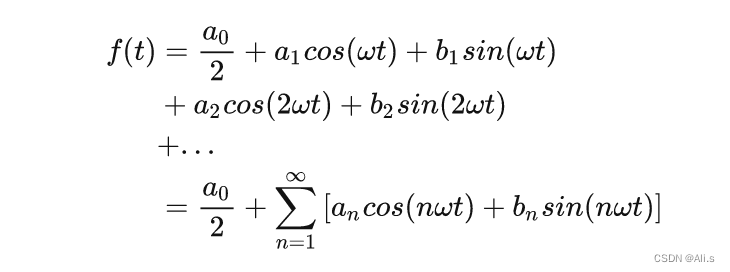 仔细观察上面的式子,不难发现,信号
仔细观察上面的式子,不难发现,信号f(t)其实就是一些不同频率的正弦函数组成相加而成,这里就是关键了,还记得上面钢琴谱的时域音乐是如何出来了的吗?正是一个个音节组合叠加而成,看到这里,你应该更加明白时域与频域的含义了,所以可以将上面的式子抽象成比较简单的式子来表达:
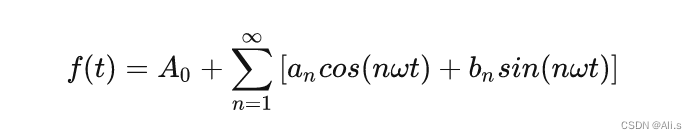 那么不难发现,简化的式子只需要解出直流分量
那么不难发现,简化的式子只需要解出直流分量A0和傅里叶级数系数an、bn,就能够确定出信号。下面给出系数的计算公式:
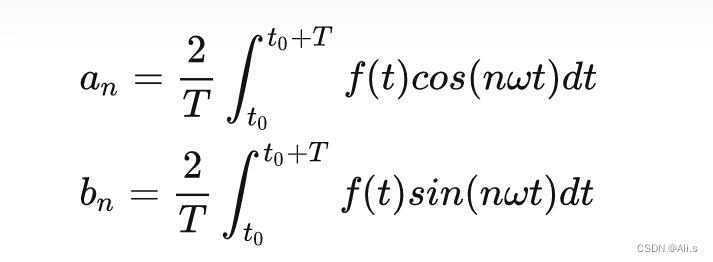
2、傅里叶级数的频谱
通过上面傅里叶级数的理解,可以看出任何信号都是正弦波的叠加,那么相当于同一个正弦波做不同的振荡,是不是就可以对信号进行合成,下面有个神奇的动图,很好的展示了这个特点,
 下面一起来看一下矩形波是如何形成的,简单的使用
下面一起来看一下矩形波是如何形成的,简单的使用MATLAB进行一下仿真模拟;
x=0:pi/4:6*pi;
for step=1:2:50
f=0;
for i=1:2:step
f = f+1/i*sin(i*x);
end
plot(f);
set(figure(1));
filename=[num2str(step)];
print(1,filename);
end
随着叠加的递增,所有正弦波中上升的部分逐渐让原本缓慢增加的曲线不断变陡,而所有正弦波中下降的部分又抵消了上升到最高处时继续上升的部分使其变为水平线。一个矩形就这么叠加而成了,由傅里叶级数公式可知,如果需要做成一个标准的矩形波,那需要n无限大,所以是不可能完成的,只能对其进行大致模拟,主要是这种思想,真是思想有多远,就能走多远。

3、傅里叶级数的条件
说了这么多,感觉是不是已经懂了傅里叶级数的内容,那么你肯定已经知道信号可以通过一系列的正弦波叠加而成,而正弦波都是周期信号,所以能够使用傅里叶展开的信号必然是周期信号。一般我们遇到的周期信号都能满足狄利克雷条件,这里引入了狄利克雷条件:
(1)在一周期内,只有有限个第一类间断点;
(2)在一周期内,极值数目应是有限个;
(3)在一周期内,信号是绝对可积的。
可去间断点:函数在该点左极限、右极限存在且相等,但不等于该点函数值或函数在该点无定义。跳跃间断点:函数在该点左极限、右极限存在但不相等。可去间断点和跳跃间断点称为第一类间断点。
三、傅里叶变换
1、傅里叶变换的理解
既然傅里叶级数这么强,那么还需要傅里叶变换干什么呢,当然是来解决非周期信号的问题了,由于傅里叶级数是对周期信号进行处理的,利用这样的傅立叶级数展开可以得到信号的频率分量,然而对于非周期信号我们没法傅立叶级数展开,因为不满足狄利克雷条件,所以我们利用引入频谱密度这样的方法来处理,这个在下一篇频域性质分析中会提及到。下面给出傅里叶变换的公式:
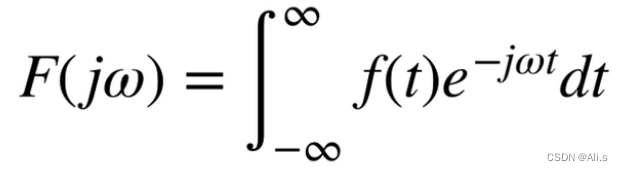 如果你已经理解了傅里叶级数的一切,那么傅里叶变换就会非常简单了。一个时间函数的傅里叶变换是一个频率的复值函数,其大小代表了原始函数中存在的该频率的数量,其参数是该频率的基本正弦波的相位偏移。傅里叶变换不限于时间函数,但原始函数的域就是前面提到的时域。
如果你已经理解了傅里叶级数的一切,那么傅里叶变换就会非常简单了。一个时间函数的傅里叶变换是一个频率的复值函数,其大小代表了原始函数中存在的该频率的数量,其参数是该频率的基本正弦波的相位偏移。傅里叶变换不限于时间函数,但原始函数的域就是前面提到的时域。
2、神奇的欧拉
欧拉公式的出现,给傅里叶变换和傅里叶级数的处理带来了非常关键的思想,下面先来看看欧拉的神奇之处,欧拉公式如下:
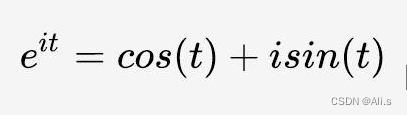
会惊奇的发现,这个式子说明一个指数函数可以写成复数域的两个正弦函数的和,这里是不是很熟练,前面的傅里叶级数是不是说过信号可以由多个正弦波叠加而成,竟然出奇的一致,这可能就是数学的魅力吧,然而更神奇的事还在后面,当t取值为π时,神奇的事情又发生了:
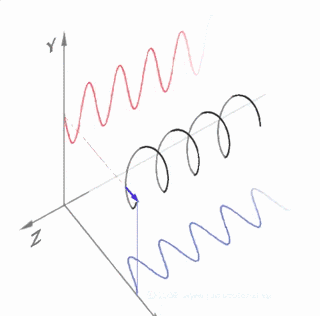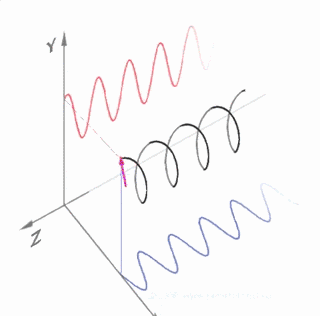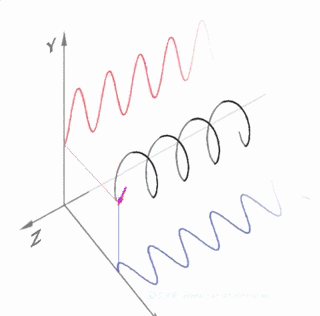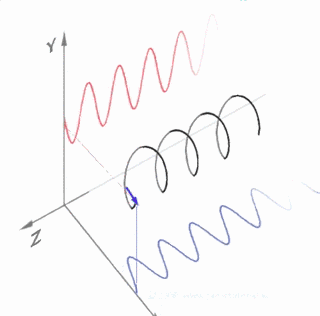
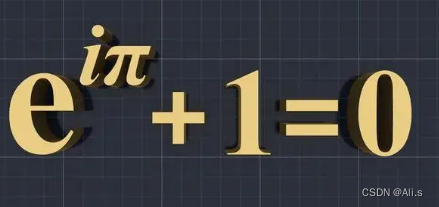 欧拉公式所要表达的是随着时间变化,在复平面上做圆周运动的点,随着时间的改变,在时间轴上就成了一条螺旋线。如果只看它的实数部分,也就是螺旋线在左侧的投影,就是一个标准余弦函数。而右侧的投影则是一个标准的正弦函数。
欧拉公式所要表达的是随着时间变化,在复平面上做圆周运动的点,随着时间的改变,在时间轴上就成了一条螺旋线。如果只看它的实数部分,也就是螺旋线在左侧的投影,就是一个标准余弦函数。而右侧的投影则是一个标准的正弦函数。
3、傅里叶级数与变换
当你看到这里,想必已经对傅里叶级数和傅里叶变换有了一个全新的认识,傅里叶级数是周期变换,傅里叶变换是一种非周期变换,傅里叶级数是以三角函数为基对周期信号的无穷级数展开,如果把周期函数的周期取作无穷大,对傅里叶级数取极限即得到傅里叶变换。傅里叶变换是从傅里叶级数推演而来的,傅里叶级数是所有周期函数都可以分解成一系列的正交三角函数。那么一起看看两者在信号的不同阶段的表现,你将会更加明白上面这绕口的表述了:
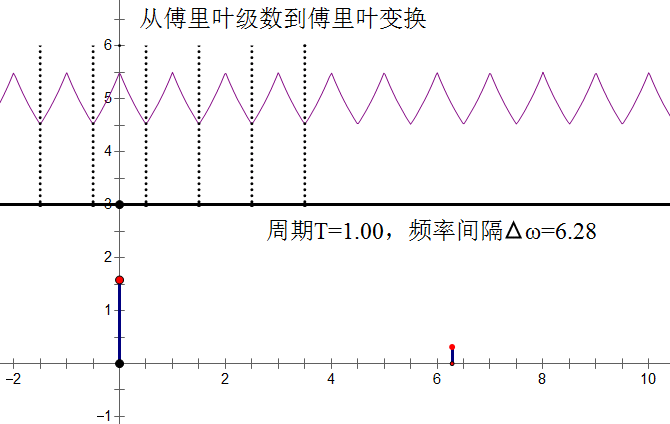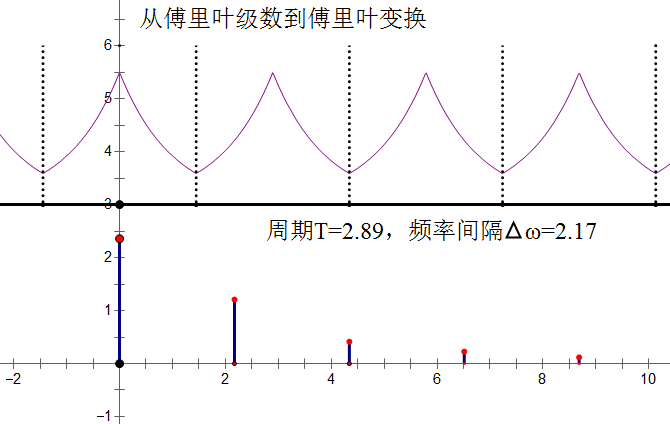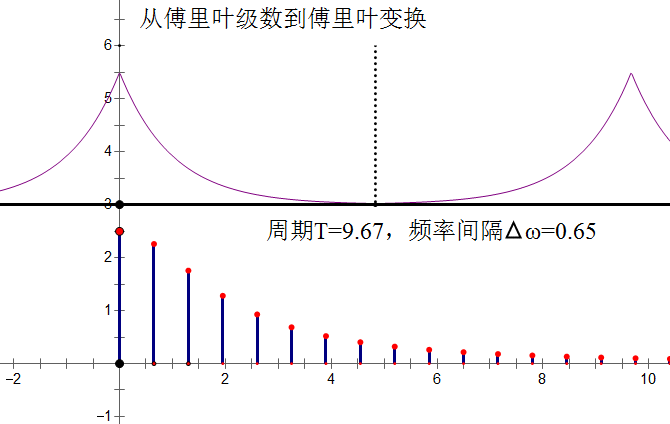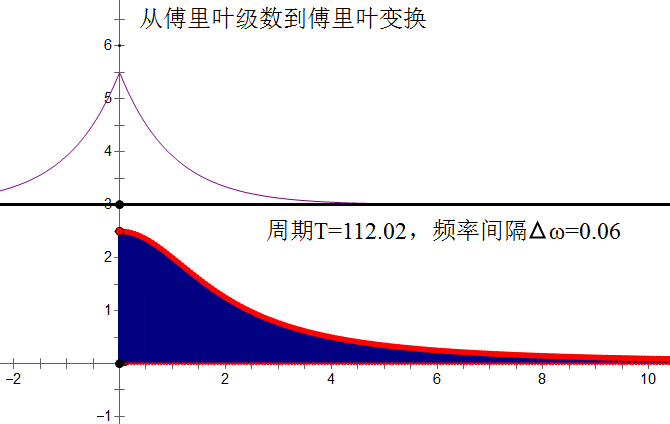 这样,周期函数对应的傅里叶级数即是它的频谱函数。需要提及的是傅里叶级数是周期信号的另一种时域的表达方式,也就是正交级数,它不同频率的波形的叠加,而傅里叶变换就是完全的频域分析。
这样,周期函数对应的傅里叶级数即是它的频谱函数。需要提及的是傅里叶级数是周期信号的另一种时域的表达方式,也就是正交级数,它不同频率的波形的叠加,而傅里叶变换就是完全的频域分析。
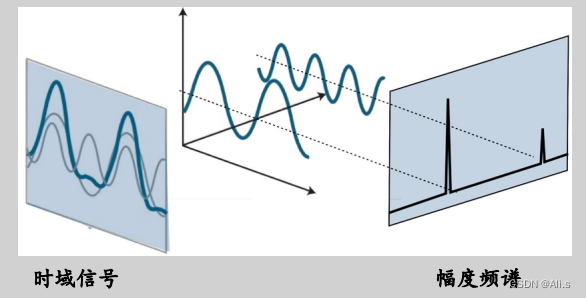 一个信号从不同的角度去观察时,便可以得出不同的特征,时域信号的周期性不确定,决定了是使用傅里叶变换还是傅里叶级数对其分析,而信号的特征有很多,幅度频谱是最常见之一。
一个信号从不同的角度去观察时,便可以得出不同的特征,时域信号的周期性不确定,决定了是使用傅里叶变换还是傅里叶级数对其分析,而信号的特征有很多,幅度频谱是最常见之一。

总结
对于周期信号利用傅立叶级数可以将其展开为很多正弦余弦信号的叠加,能清楚看出原信号所含有的频率成分,利用这样的傅立叶级数展开可以得到信号的频率分量;然而对于非周期信号我们没法傅立叶级数展开,因为不满足狄利克雷条件,所以我们利用引入频谱密度这样的方法,因为非周期信号可以认为是周期无限大的周期信号,利用这样的关系以及频谱密度的方法,然后利用欧拉公式和极限的知识,可将傅立叶级数的展开式变成了傅立叶变换的积分式,所以,傅立叶级数和傅立叶变换实际目的是相通的,就是观察信号的频率成分,以便利用频域分析的方法。
文章出处登录后可见!
