特征选择

特征选择是特征工程里的一个重要问题，其目标是寻找最优特征子集。特征选择能剔除不相关(irrelevant)或冗余(redundant )的特征，从而达到减少特征个数，提高模型精确度，减少运行时间的目的。并且常能听到“数据和特征决定了机器学习的上限，而模型和算法只是逼近这个上限而已”，由此可见其重要性。
特征选择有以下三种常见的方法：
导入数据:

import pandas as pd
data = pd.read_csv(r"C:\Users\18700\Desktop\03数据预处理和特征工程\digit recognizor.csv")
data.head()

X = data.iloc[:,1:] #特征矩阵
y = data.iloc[:,0] #标签
X.shape #维度指的是特征的数量，这个数据维度太高
#(42000, 784)
"""
这个数据量相对夸张，如果使用支持向量机和神经网络，很可能会直接跑不出来。使用KNN跑一次大概需要半个小时。
用这个数据举例，能更够体现特征工程的重要性。
"""

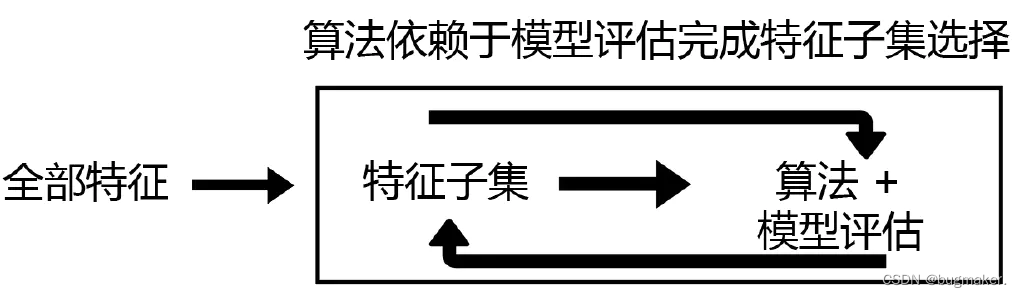
Wrapper（包装法）

基本思想：基于hold-out方法，对于每一个待选的特征子集，都在训练集上训练一遍模型，然后在测试集上根据误差大小选择出特征子集。需要先选定特定算法，通常选用普遍效果较好的算法， 例如Random Forest， SVM， kNN等等。
但是遍历所有可能的组合达到全局最优级，计算复杂度是2^n，一般是不太实际的算法。

Filter（过滤法）

Filter(过滤法)：按照发散性或相关性对各个特征进行评分，设定阈值或者待选择特征的个数进行筛选
基本想法是：分别对每个特征x，计算x相对于标签y的信息量S。然后将S按照从大到小排序，输出前k个特征。关键的问题是使用什么样的方法来度量 S？下面给出几种常见的度量方式：

Pearson相关系数

Pearson相关系数
皮尔森相关系数是一种最简单的，能帮助理解特征和变量之间关系的方法，衡量的是变量之间的线性相关性，结果的取值区间为[-1,1] ， -1 表示完全的负相关(这个变量下降，那个就会上升)， +1 表示完全的正相关， 0 表示没有线性相关性。Pearson Correlation速度快、易于计算，经常在拿到数据(经过清洗和特征提取之后的)之后第一时间就执行。Scipy的pearsonr方法能够同时计算相关系数和p-value

import numpy as np
from scipy.stats import pearsonr

np.random.seed(0)
size = 300
x = np.random.normal(0, 1, size)
print("Lower noise：", pearsonr(x, x + np.random.normal(0, 1, size)))
print("Higher noise：", pearsonr(x, x + np.random.normal(0, 10, size)))

from sklearn.feature_selection import SelectKBest
# 选择K个最好的特征，返回选择特征后的数据
# 第一个参数为计算评估特征是否好的函数，该函数输入特征矩阵和目标向量，输出二元组（评分，P值）的数组，数组第i项为第i个特征的评分和P值。在此定义为计算相关系数
# 参数k为选择的特征个数
SelectKBest(lambda X, Y: array(map(lambda x:pearsonr(x, Y), X.T)).T, k=2).fit_transform(iris.data, iris.target)

Pearson相关系数的一个明显缺陷是，作为特征排序机制，他只对线性关系敏感。如果关系是非线性的，即便两个变量具有一一对应的关系，Pearson相关性也可能会接近 0 。

卡方验证

卡方过滤是专门针对离散型标签（即分类问题）的相关性过滤。卡方检验类feature_selection.chi2计算每个非负特征和标签之间的卡方统计量，并依照卡方统计量由高到低为特征排名。再结合feature_selection.SelectKBest这个可以输入”评分标准“来选出前K个分数最高的特征的类，我们可以借此除去最可能独立于标签，与我们分类目的无关的特征。

from sklearn.ensemble import RandomForestClassifier as RFC
from sklearn.model_selection import cross_val_score
from sklearn.feature_selection import SelectKBest #选择k个分数最高的特征
from sklearn.feature_selection import chi2 #卡方检验

#假设在这里我需要300个特征
X_fschi = SelectKBest(chi2, k=300).fit_transform(X_fsvar, y) #选择前300个卡方值的特征
X_fschi.shape
#(42000, 300)

验证模型的效果如何

cross_val_score(RFC(n_estimators=10,random_state=0),X_fschi,y,cv=5).mean()

输出结果：

0.9344761904761905
'''
如果模型的效果降低了，这说明我们在设定k=300的时候删除了与模型相关且有效的特征，
我们的K值设置得太小，要么我们需要调整K值，要么我们必须放弃相关性过滤。
'''

互信息法

互信息法是用来捕捉每个特征与标签之间的任意关系（包括线性和非线性关系）的过滤方法。和F检验相似，它既可以做回归也可以做分类，并且包含两个类feature_selection.mutual_info_classif（互信息分类）和feature_selection.mutual_info_regression（互信息回归）。
它返回“每个特征与目标之间的互信息量的估计”，这个估计量在[0,1]之间取值，为0则表示两个变量独立，为1则表示两个变量完全相关。

from sklearn.feature_selection import mutual_info_classif as MIC
result = MIC(X_fsvar,y)
k = result.shape[0] - sum(result <= 0)
#X_fsmic = SelectKBest(MIC, k=填写具体的k).fit_transform(X_fsvar, y)
#cross_val_score(RFC(n_estimators=10,random_state=0),X_fsmic,y,cv=5).mean()

方差选择法

过滤特征选择法还有一种方法不需要度量特征 x 和标签 y 的信息量。这种方法先要计算各个特征的方差，然后根据阈值，选择方差大于阈值的特征。优先消除方差为0的特征。VarianceThreshold有重要参数threshold，表示方差的阈值，表示舍弃所有方差小于threshold的特征，不填默认为0，即删除所有的记录都相同的特征。
VarianceThreshold:

from sklearn.feature_selection import VarianceThreshold
selector = VarianceThreshold() #实例化，不填参数默认方差为0
X_var0 = selector.fit_transform(X) #获取删除不合格特征之后的新特征矩阵
#也可以直接写成 X = VairanceThreshold().fit_transform(X)
X_var0.shape #是一个ndarray
#(42000, 708) #可将特征变少了，删除了方差为0的特征

#X_var0.head() #会报错
pd.DataFrame(X_var0).head() #所以需要转换为dataframe

根据方差的中位数进行过滤

#通过var的中位数进行过滤
import numpy as np
X_fsvar = VarianceThreshold(np.median(X.var().values)).fit_transform(X) #就是舍弃方差小于中位数方差的特征
#X.var()是一个series，.values提取对应的值
X.var().values
np.median(X.var().values)
X_fsvar.shape
#(42000, 392)

特征是伯努利随机变量(二分类)

#若特征是伯努利随机变量，假设p=0.8，即二分类特征中某种分类占到80%以上的时候删除特征
X_bvar = VarianceThreshold(.8 * (1 - .8)).fit_transform(X)
X_bvar.shape
#(42000, 685)

方差选择的逻辑并不是很合理，这个是基于各特征分布较为接近的时候，才能以方差的逻辑来衡量信息量。但是如果是离散的或是仅集中在几个数值上，如果分布过于集中，其信息量则较小。而对于连续变量，由于阈值可以连续变化，所以信息量不随方差而变。 实际使用时，可以结合cross-validate进行检验

Embedded(嵌入法）

Embedded(嵌入法)：先使用某些机器学习的模型进行训练，得到各个特征的权值系数，根据系数从大到小选择特征（类似于Filter，只不过系数是通过训练得来的）
基于惩罚项的特征选择法 通过L1正则项来选择特征：L1正则方法具有稀疏解的特性，因此天然具备特征选择的特性。

feature_selection.SelectFromModel

class sklearn.feature_selection.SelectFromModel (estimator, threshold=None, prefit=False, norm_order=1,max_features=None)
#estimator：使用的模型评估器，只要是带feature_importances_或者coef_属性，或带有l1和l2惩罚项的模型都可以使用。
#threshold：特征重要性的阈值，重要性低于这个阈值的特征都将被删除。

from sklearn.feature_selection import SelectFromModel 
from sklearn.ensemble import RandomForestClassifier as RFC

RFC_ = RFC(n_estimators =10,random_state=0) #需要先实例化随机森林，再带入SelectFromModel。
X_embedded = SelectFromModel(RFC_,threshold=0.005).fit_transform(X,y) #这个是嵌入法的实例化
#在这里我只想取出来有限的特征。0.005这个阈值对于有780个特征的数据来说，是非常高的阈值，因为平均每个特征只能够分到大约0.001的feature_importances_
X_embedded.shape
#(42000, 47)  模型的维度明显被降低了

绘制threshold的学习曲线

import numpy as np
import matplotlib.pyplot as plt

RFC_.fit(X,y).feature_importances_ #看特征重要性
#linspace(小值，大值，个数) 在最大值和最小值之间取20个数
threshold = np.linspace(0,(RFC_.fit(X,y).feature_importances_).max(),20) #让阈值的取值在0到最大值之间取出20个数

score = []
for i in threshold:
    X_embedded = SelectFromModel(RFC_,threshold=i).fit_transform(X,y)
    once = cross_val_score(RFC_,X_embedded,y,cv=5).mean()
    score.append(once)

plt.plot(threshold,score)
plt.show()

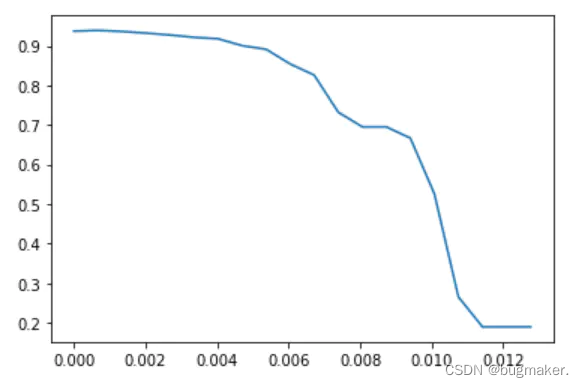
X_embedded = SelectFromModel(RFC_,threshold=0.00067).fit_transform(X,y)
X_embedded.shape
#(42000, 324)

cross_val_score(RFC_,X_embedded,y,cv=5).mean()
#0.9391190476190475