目录
一、MPC模型
1.1车辆运动学模型
在车辆运动学建模时先简化汽车,用前后轮和车轴表示,即为自行车模型。车轮的转角用表示,车轴长用L表示,汽车转弯可以近似为后轮绕某一点做圆周运动。推导如下:
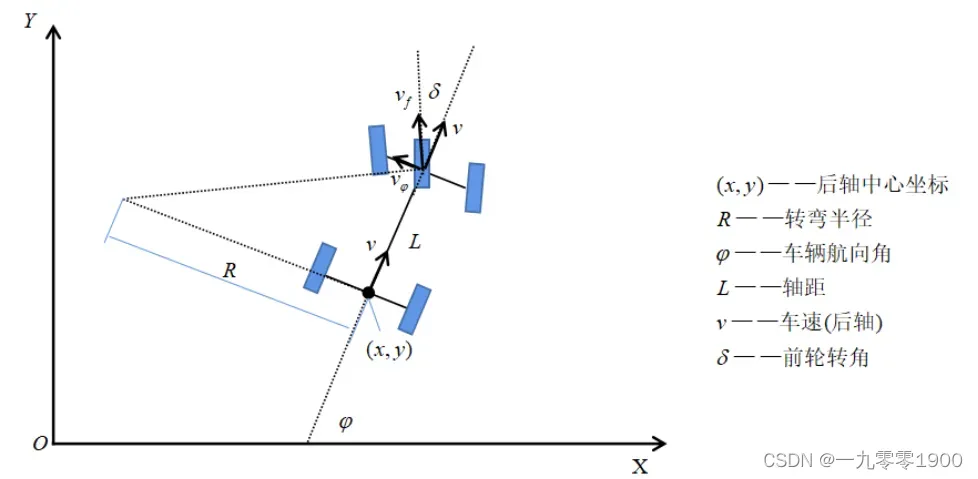
转弯半径:
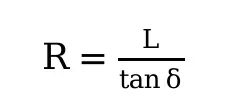 (1)
(1)
其中为车速,为车辆航向,则航向角速度:
![]() (2)
(2)
根据几何关系,x方向的横向速度
![]() (3)
(3)
y方向的纵向速度:
![]() (4)
(4)
联立(1)-(4)得阿克曼转向的车辆运动学模型:
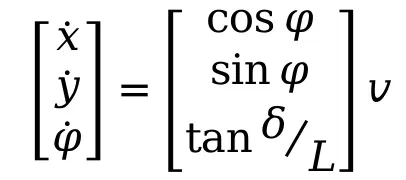 (5)
(5)
1.2模型线性化
得到的状态方程有三角函数和乘法操,是一个非线性方程,要先使用泰勒展开进行线性化。取生成的路径上的某一点进行泰勒展开,取第一阶即可完成线性化的过程。
令,,线性化将运动学模型在此刻运动学方程在参考点泰勒展开:
![]() (6)
(6)
车状态:
![]() (7)
(7)
其中雅可比矩阵A,B:
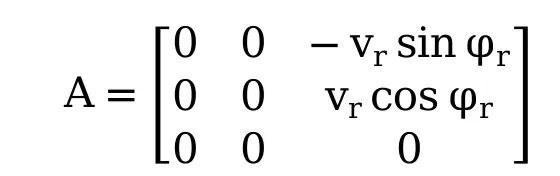 (8)
(8)
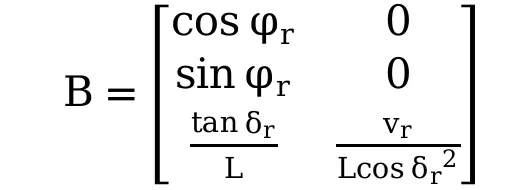 (9)
(9)
1.3模型离散化
带入式(7)进行离散化
![]() (10)
(10)
![]() (11)
(11)
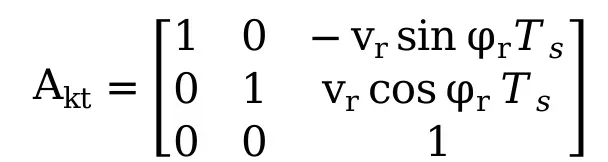 (12)
(12)
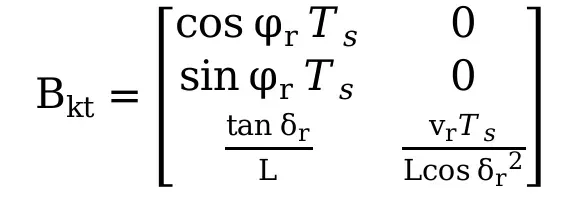 (13)
(13)
则车辆运动学模型离散为:
![]() (14)
(14)
1.4预测
假设预测当前时刻后的n个时刻,未来状态只与当前状态和过程控制量有关。
![]() (15)
(15)
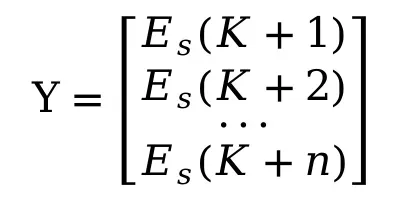 (16)
(16)
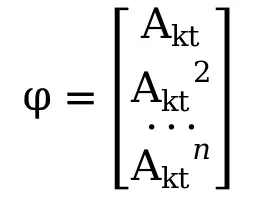 (17)
(17)
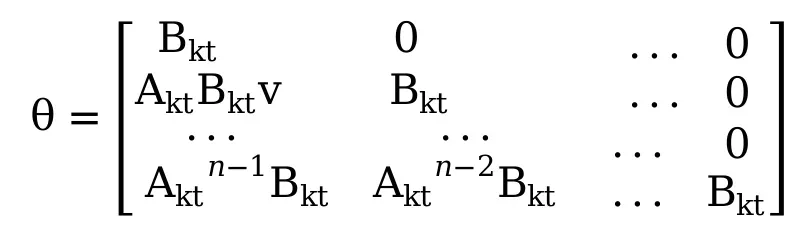 (18)
(18)
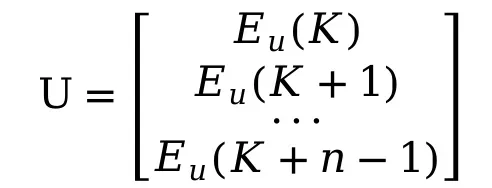 (19)
(19)
则预测公式为
![]() (20)
(20)
1.5最优化
当前状态已知,求解最优U使目标函数最小。针对状态方程(20),取式(19)误差平方和最小,则目标函数为:
![]() (21)
(21)
使用python库函数的cvxopt求解。
二、多线程通信
mpc程序发布控制消息指令,updatestate程序接收指令,更新车辆状态,发布给mpc程序,实现两者的ros通信。在主程序中定义函数thread_job()实现ros通信的多线程。当主函数运行的时候,给rospy额外开启一个线程处理收发ros消息。用户在图像上选择可行驶区域引导点,通过ros消息发布给mpc控制程序,mpc程序不断接受ros消息,并保存拟合成可行驶的三次曲线。具体实现如下:
def thread_job(): #多线程
rospy.Subscriber('chatter', Float64MultiArray, callback)
rospy.spin()
if __name__=='__main__':
add_thread = threading.Thread(target = thread_job)
add_thread.start()三、用户交互
用户可以自己导入所需的图片
在终端依次运行
roscore和
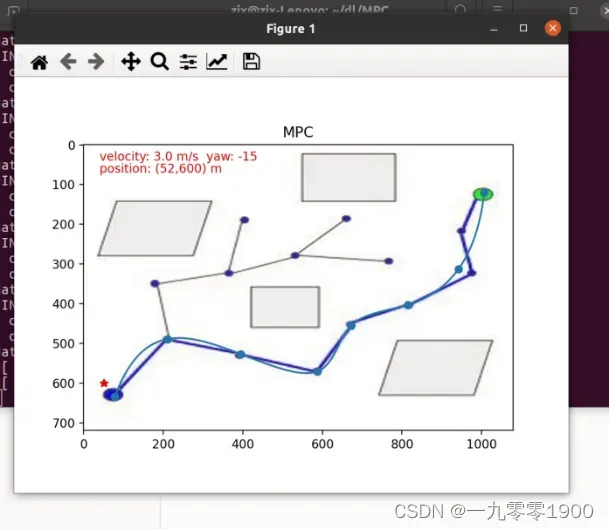
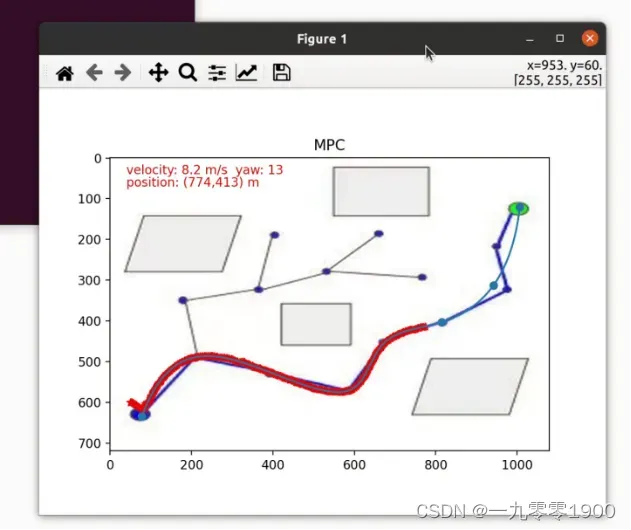
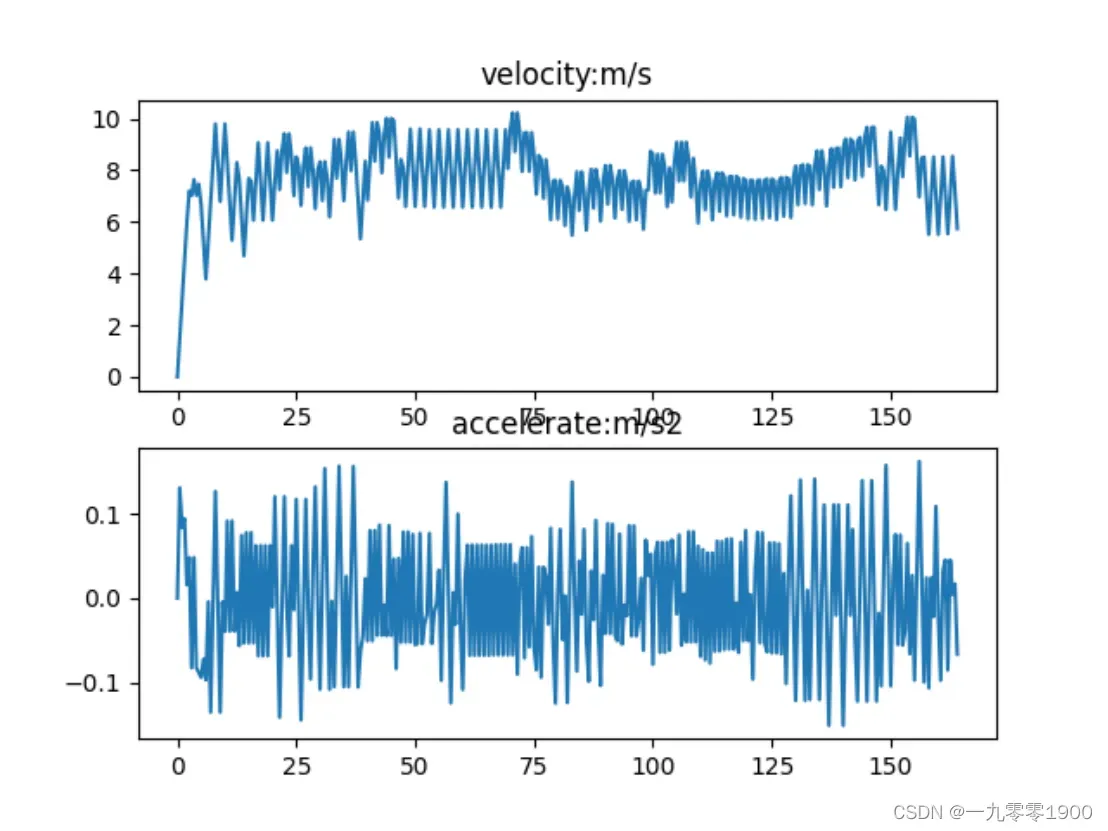
bash start.sh即可进入选择图像上可通行区域的引导点(4个+)。按回车确认,程序即可自动启动拟合曲线。运行MPC控制程序引导小车完成轨迹跟踪,其中左上角实时显示当前位置、车速和航向角。轨迹跟踪结束后,自动生成跟踪过程的车速和加速度。
所有代码
代码链接Link:https://github.com/zuojixiang/MPC_carcontrol.git
mpc.py主程序
import matplotlib.pyplot as plt
import numpy as np
from math import *
from cvxopt import matrix, solvers
from scipy.interpolate import interp1d
import cv2
import rospy
from std_msgs.msg import Float64MultiArray, Float64
import threading
import time
from PIL import ImageFont, ImageDraw, Image
class MPC:
def __init__(self):
self.Np = 60 # 预测步长
self.Nc = 60 # 控制步长
self.dt = 0.5 # 时间间隔
self.Length = 1.0 # 车辆轴距
max_steer = 30 * pi / 180 # 最大方向盘打角
max_steer_v = 15 * pi / 180 # 最大方向盘打角速度
max_v = 12#8.7 # 最大车速
max_a = 3.0 # 最大加速度
# 目标函数相关矩阵
self.Q = 50 * np.identity(3*self.Np) # 位姿权重
self.R = 100 * np.identity(2*self.Nc) # 控制权重
self.kesi = np.zeros((5, 1))
self.A = np.identity(5)
self.B = np.block([
[np.zeros((3, 2))],
[np.identity(2)]
])
self.C = np.block([
[np.identity(3), np.zeros((3, 2))]
])
self.PHI = np.zeros((3*self.Np, 5))
self.THETA = np.zeros((3*self.Np, 2*self.Nc))
self.CA = (self.Np+1) * [self.C]
self.H = np.zeros((2*self.Nc, 2*self.Nc))
self.f = np.zeros((2*self.Nc, 1))
# 不等式约束相关矩阵
A_t = np.zeros((self.Nc, self.Nc))
for p in range(self.Nc):
for q in range(p+1):
A_t[p][q] = 1
A_I = np.kron(A_t, np.identity(2))
# 控制量约束
umin = np.array([[-max_v], [-max_steer]])
umax = np.array([[max_v], [max_steer]])
self.Umin = np.kron(np.ones((self.Nc, 1)), umin)
self.Umax = np.kron(np.ones((self.Nc, 1)), umax)
# 控制增量约束
delta_umin = np.array([[-max_a * self.dt], [-max_steer_v * self.dt]])
delta_umax = np.array([[max_a * self.dt], [max_steer_v * self.dt]])
delta_Umin = np.kron(np.ones((self.Nc, 1)), delta_umin)
delta_Umax = np.kron(np.ones((self.Nc, 1)), delta_umax)
self.A_cons = np.zeros((2 * 2*self.Nc, 2*self.Nc))
self.A_cons[0:2*self.Nc, 0:2*self.Nc] = A_I
self.A_cons[2*self.Nc:4*self.Nc, 0:2*self.Nc] = np.identity(2*self.Nc)
self.lb_cons = np.zeros((2 * 2*self.Nc, 1))
self.lb_cons[2*self.Nc:4*self.Nc, 0:1] = delta_Umin
self.ub_cons = np.zeros((2 * 2*self.Nc, 1))
self.ub_cons[2*self.Nc:4*self.Nc, 0:1] = delta_Umax
def mpcControl(self, x, y, yaw, v, angle, tar_x, tar_y, tar_yaw, tar_v, tar_angle): # mpc优化控制
T = self.dt
L = self.Length
# 更新误差
self.kesi[0][0] = x-tar_x
self.kesi[1][0] = y-tar_y
self.kesi[2][0] = self.normalizeTheta(yaw - tar_yaw)
self.kesi[3][0] = v - tar_v
self.kesi[4][0] = angle - tar_angle
# 更新A矩阵
self.A[0][2] = -tar_v * sin(tar_yaw) * T
self.A[0][3] = cos(tar_yaw) * T
self.A[1][2] = tar_v * cos(tar_yaw) * T
self.A[1][3] = sin(tar_yaw) * T
self.A[2][3] = tan(tar_angle) * T / L
self.A[2][4] = tar_v * T / (L * (cos(tar_angle)**2))
# 更新B矩阵
self.B[0][0] = cos(tar_yaw) * T
self.B[1][0] = sin(tar_yaw) * T
self.B[2][0] = tan(tar_angle) * T / L
self.B[2][1] = tar_v * T / (L * (cos(tar_angle)**2))
# 更新CA
for i in range(1, self.Np+1):
self.CA[i] = np.dot(self.CA[i-1], self.A)
# 更新PHI和THETA
for j in range(self.Np):
self.PHI[3*j:3*(j+1), 0:5] = self.CA[j+1]
for k in range(min(self.Nc, j+1)):
self.THETA[3*j:3*(j+1), 2*k: 2*(k+1)
] = np.dot(self.CA[j-k], self.B)
# 更新H
self.H = np.dot(np.dot(self.THETA.transpose(), self.Q),
self.THETA) + self.R
# 更新f
self.f = 2 * np.dot(np.dot(self.THETA.transpose(), self.Q),
np.dot(self.PHI, self.kesi))
# 更新约束
Ut = np.kron(np.ones((self.Nc, 1)), np.array([[v], [angle]]))
self.lb_cons[0:2*self.Nc, 0:1] = self.Umin-Ut
self.ub_cons[0:2*self.Nc, 0:1] = self.Umax-Ut
# 求解QP
P = matrix(self.H)
q = matrix(self.f)
G = matrix(np.block([
[self.A_cons],
[-self.A_cons]
]))
h = matrix(np.block([
[self.ub_cons],
[-self.lb_cons]
]))
solvers.options['show_progress'] = False
sol = solvers.qp(P, q, G, h)
X = sol['x']
# 输出结果
v += X[0]
angle += X[1]
return v, angle
def normalizeTheta(self, angle): # 角度归一化
while(angle >= pi):
angle -= 2*pi
while(angle < -pi):
angle += 2*pi
return angle
def findIdx(self, x, y, cx, cy): # 寻找欧式距离最近的点
min_dis = float('inf')
idx = 0
for i in range(len(cx)):
dx = x - cx[i]
dy = y - cy[i]
dis = dx**2 + dy**2
if(dis < min_dis):
min_dis = dis
idx = i
return idx
'''def update(self, x, y, yaw, v, angle): # 模拟车辆位置
x += v * cos(yaw) * self.dt
y += v * sin(yaw) * self.dt
yaw += v / self.Length * tan(angle) * self.dt
return x, y, yaw'''
wps= []
def callback(data):
wps.append(data.data) # data.data是取出一维数组
def callbackux(ux):
global x
x=ux.data
def callbackuy(uy):
global y
y=uy.data
def callbackuyaw(uyaw):
global yaw
yaw=uyaw.data
def thread_job(): #多线程
rospy.Subscriber('chatter', Float64MultiArray, callback)
rospy.spin()
if __name__ == '__main__':
rospy.init_node('listener', anonymous=True)
add_thread = threading.Thread(target = thread_job)
add_thread.start()
time.sleep(25)
wps=np.transpose(wps)
print(wps)
x = wps[0]
y = wps[1]
t = np.linspace(0, 1, num=len(x))
f1 = interp1d(t,x,kind='cubic')
f2 = interp1d(t,y,kind='cubic')
newt = np.linspace(0,1,100)
cx = f1(newt)
cy = f2(newt)
dx = np.zeros(len(cx))
ddx = np.zeros(len(cy))
cyaw = np.zeros(len(cx))
ck = np.zeros(len(cx))
# 计算一阶导数
for i in range(len(cx)-1):
dx[i] = (cy[i+1] - cy[i])/(cx[i+1] - cx[i])
dx[len(cx)-1] = dx[len(cx)-2]
# 计算二阶导数
for i in range(len(cx)-2):
ddx[i] = (cy[i+2] - 2*cy[i+1] + cy[i]) / (0.5 * (cx[i+2] - cx[i]))**2
ddx[len(cx)-2] = ddx[len(cx)-3]
ddx[len(cx)-1] = ddx[len(cx)-2]
# 计算偏航角
for i in range(len(cx)):
cyaw[i] = atan(dx[i])
# 计算曲率
for i in range(len(cx)):
ck[i] = ddx[i] / (1 + dx[i]**2)**1.5
# 初始状态
x = 50.0
y = 600.0
yaw = 0.0
v = 0.0
angle = 0.0
t = 0
# 历史状态
xs = [x]
ys = [y]
vs = [v]
angles = [angle]
ts = [t]
pubx = rospy.Publisher('chatterx', Float64, queue_size=10)
puby = rospy.Publisher('chattery', Float64, queue_size=10)
pubyaw = rospy.Publisher('chatteryaw', Float64, queue_size=10)
pubv = rospy.Publisher('chatterv', Float64, queue_size=10)
pubangle = rospy.Publisher('chatterangle', Float64, queue_size=10)
# 实例化
mpc = MPC()
while(1):
idx = mpc.findIdx(x, y, cx, cy)
if(idx == len(cx)-1):
break
tar_v = 30.0/3.6
tar_angle = atan(mpc.Length * ck[idx])
(v, angle) = mpc.mpcControl(x, y, yaw, v, angle,
cx[idx], cy[idx], cyaw[idx], tar_v, tar_angle)
pubx.publish(x) # 发布数据
#rospy.loginfo(x) # 输出数据
puby.publish(y)
#rospy.loginfo(y)
pubyaw.publish(yaw)
#rospy.loginfo(yaw)
pubv.publish(v)
#rospy.loginfo(v)
pubangle.publish(angle)
#rospy.loginfo(angle)
#订阅车辆状态
rospy.Subscriber('/upstatex', Float64, callbackux)
rospy.Subscriber('/upstatey', Float64, callbackuy)
rospy.Subscriber('/upstateyaw', Float64, callbackuyaw)
#(x, y, yaw) = mpc.update(x, y, yaw, v, angle)
ve='velocity: '+str(round(v,1))+' m/s'+' yaw: '+str(int(-yaw/3.14*180))
po='position: '+'('+str(int(x))+','+str(int(y))+')'+' m'
# 保存状态
xs.append(x)
ys.append(y)
vs.append(v)
angles.append(angle)
t = t+0.5
ts.append(t)
# 显示
img1 = cv2.imread('1.png')
plt.title("MPC")
plt.text(40, 40, ve, color='red')
plt.text(40, 70, po, color='red')
plt.imshow(img1)
plt.scatter(wps[0], wps[1])
plt.plot(cx, cy)
plt.scatter(xs, ys, c='r', marker='*')
plt.pause(0.01) # 暂停0.01秒
plt.clf()
plt.close()
plt.subplot(2, 1, 1)
plt.title("velocity:m/s")
plt.plot(ts, vs)
plt.subplot(2, 1, 2)
plt.title("accelerate:m/s2")
plt.plot(ts, angles)
plt.show()click_points.py程序
import cv2 as cv
import os
import rospy
import time
import numpy as np
from std_msgs.msg import Float64MultiArray, Int16
from cv_bridge import CvBridge , CvBridgeError
maxsize = (1080, 720) # 定义图片放缩大小
img = cv.imread('1.png')
img = cv.resize(img, maxsize, cv.INTER_AREA)
os.remove('points.txt')
# 鼠标事件
def on_EVENT_LBUTTONDOWN(event, x, y, flags, param):
if event == cv.EVENT_LBUTTONDOWN:
xy = "%d,%d" % (x, y)
# 画圈(图像:img,坐标位置:xy,半径:1(就是一个点),颜色:蓝,厚度:-1(就是实心)
cv.circle(img, (x, y), 1, (255, 0, 0), thickness=-1)
cv.putText(img, xy, (x, y), cv.FONT_HERSHEY_PLAIN, 1.0, (0, 0, 0), thickness=1)
cv.imshow("click some points with mouse to pass!", img)
#写入txt
x_str = str(x)
y_str = str(y)
f = open(r"points.txt", "a+")
f.writelines(x_str + ' ' + y_str + '\n')
cv.namedWindow("click some points with mouse to pass!")
cv.resizeWindow("click some points with mouse to pass!", 800, 600) #设置窗口大小
cv.setMouseCallback("click some points with mouse to pass!", on_EVENT_LBUTTONDOWN)
cv.imshow("click some points with mouse to pass!", img)
#回车键退出
key=1
while (key!=13):
key = cv.waitKey(1) & 0xFF
break
cv.waitKey(0)
cv.destroyAllWindows()
data_list = np.loadtxt("points.txt")
n=np.shape(data_list)[0]
print(data_list)
rospy.init_node('talker', anonymous=True)
pub = rospy.Publisher('chatter', Float64MultiArray, queue_size=10)
rate = rospy.Rate(10)
time.sleep(0.5)
for i in range(n):
data = Float64MultiArray(data=data_list[i]) # 二维数组依次发送
pub.publish(data) # 发布数据
rospy.loginfo(data) # 输出数据
rate.sleep()updatestate.py程序
from std_msgs.msg import Float64
import time
import rospy
from math import *
rospy.init_node('listener1', anonymous=True)
pubupx = rospy.Publisher('upstatex', Float64, queue_size=10)
pubupy = rospy.Publisher('upstatey', Float64, queue_size=10)
pubupyaw = rospy.Publisher('upstateyaw', Float64, queue_size=10)
dt = 0.5 # 时间间隔
Length = 1.0 # 车辆轴距
x = 50.0
y = 600.0
yaw = 0.0
v = 0.0
angle = 0.0
def callbackx(xx):
global x
x=xx.data
def callbacky(yy):
global y
y=yy.data
def callbackyaw(yyaw):
global yaw
yaw=yyaw.data
def callbackv(vv):
global v
v=vv.data
def callbackangle(aangle):
global angle
angle=aangle.data
while(1):
rospy.Subscriber('/chatterx', Float64, callbackx)
rospy.Subscriber('/chattery', Float64, callbacky)
rospy.Subscriber('/chatteryaw', Float64, callbackyaw)
rospy.Subscriber('/chatterv', Float64, callbackv)
rospy.Subscriber('/chatterangle', Float64, callbackangle)
#更新车辆状态
x += v * cos(yaw) * dt
y += v * sin(yaw) * dt
yaw += v / Length * tan(angle) * dt
pubupx.publish(x) # 发布数据
#rospy.loginfo(x) # 输出数据
pubupy.publish(y)
#rospy.loginfo(y)
pubupyaw.publish(yaw)
#rospy.loginfo(yaw)
time.sleep(0.2)#延迟200ms发送start.sh启动文件
#!/bin/bash
python3 updatestate.py&
python3 click_points.py&
python3 mpc.py
存在问题
当规划轨迹期望航向角大于90度时,MPC控制程序会崩溃陷入死循环,原因在于当计算期望航向角时,用的atan函数,其范围为(-90,90),当范围扩展到(-180,180)时,才能跟踪航向角大于90度的路径。
文章出处登录后可见!
