上次我们介绍了多层感知机(MLP),本次将介绍深度学习领域中第二个基本的模型:卷积神经网络(CNN)。CNN在MLP之上又引入了两种新的层:卷积层和池化层。
一、简介
1.1 大脑皮层中的局部检测器和平移不变性
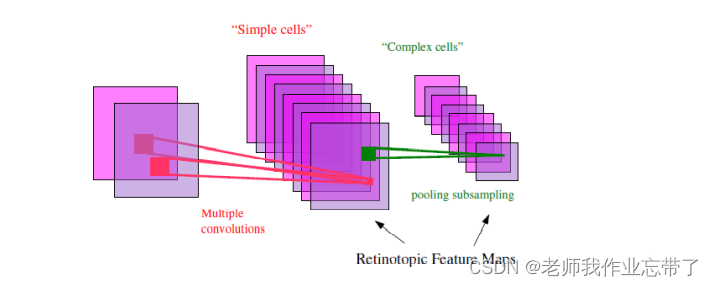
神经科学家 Hubel 和 Wiesel 于1962在猫的视觉皮层上面发现:
有一种简单细胞用于检测图像物体的局部特征;
另外一种复杂细胞将视网膜上向邻近的简单视网膜的输出“池化”。
按照他们的发现,构造出如下概念模型:
由此提出人工视觉系统的构建方式:
- 组合多个简单细胞/复杂细胞层
- 高层用来计算更全局、不变性更强的特征
- 在顶层添加分类器
从而人们建立了多个模型:
- Neocognitron模型 [Fukushima 1971-1982]
- 卷积网络 [LeCun 1988]
- HMAX模型 [Poggio 2002-2006]
- fragment hierarchy模型 [Ullman 2002-2006]
- HMAX模型 [Lowe 2006]
我们先简单介绍下Neocognitron模型从而了解一下卷积网络模型,后面的模型由于使用较少,本次不进行介绍。
1.2 Neocognitron模型
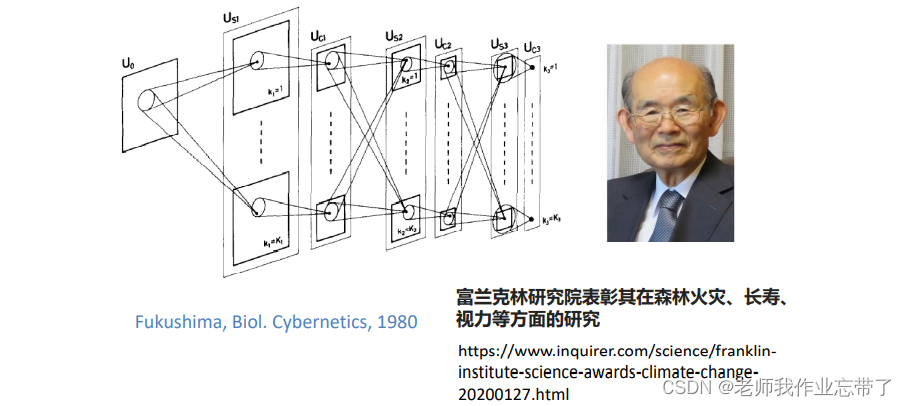
其中U0为输入层
- 之后Us1为简单细胞层,用来检测物体的一些局部信息,
- 之后Uc1复杂细胞层对局部信息进行一些融合(池化pool),
- 再之后Us2–>Uc2–>Us3–>Uc3…
我们所学的CNN结构上与这个模型基本上是一样的,主要的区别是:该模型提出时,还没有后向传播算法(BP)或BP还没有被重视。
1.3 卷积神经网络(Convolutional neural network, CNN)
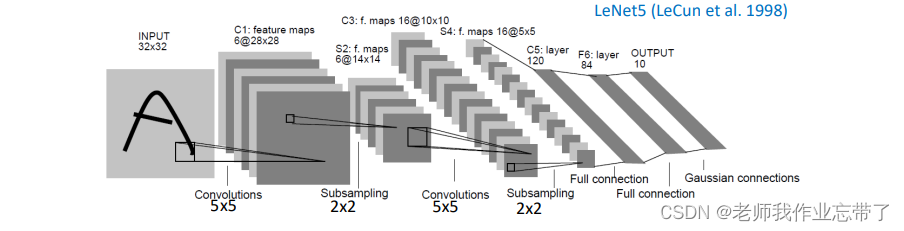
如图:
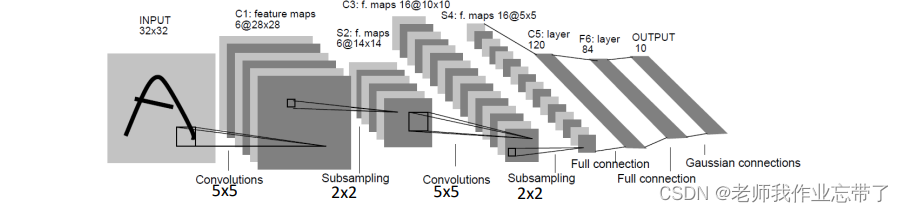
- 其中32*32的矩阵(如图片A)是输入层,
- 之后C1卷积层对应简单细胞层
- 输出
其中
是窗口大小,f 是 sigmoid 函数,w和b是卷积层参数。
- 之后S2层下采样(池化)对应复杂细胞层
- 输出
(如今我们在池化层很少用激活函数了)
- 再之后C3–>S4->C5–>S6…->MLP
注:C1对Input进行卷积,输入就是一个二维矩阵;C3对S2进行卷积,此时输入一个张量(tensor).
卷积层有两个主要的特点:
- 局部连接:它不像MLP全连接,如上图C1层某一处神经元只与前一层的一部分(5×5)连接。
- 权值共享:C1层28×28的图上每一点都是一个神经元,每个神经元都与前面的25个值相连,其25个值对应的权值/参数都是相同的。
1.4 CNN与MLP的区别
经过上面我们就可以看到,CNN相比于MLP多出了两种层:卷积层和池化层。
卷积池化处理完毕之后衔接全连接层。
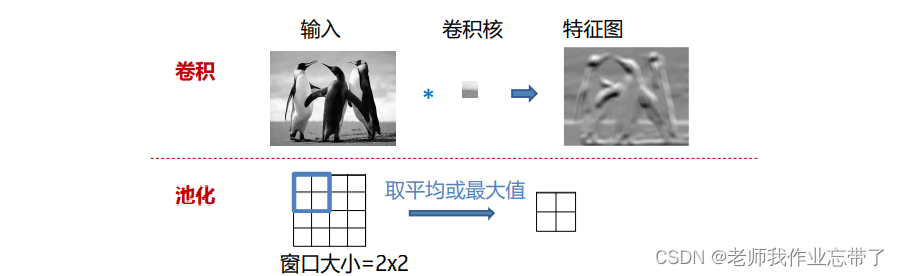
卷积:对于一个输入,我们给它一个卷积核(如上上图5×5个元素还有那25个参数w)在输入图片上进行滑动,求一个响应结果,得到一个相应图片或叫特征图片。图片上的亮度表示每个相应值得大小。
池化:把前一层得输入变小,如把4×4中四个角对应的2×2进行一下取最大(或平均或随机),这样4×4就变成了2×2。
接下来我们详细介绍一下卷积层和池化层及其前向计算,目的是让大家了解其工作原理。
至于后向计算感兴趣朋友的可以自行了解。当然也有很多优秀的工具库我们可以直接拿来用以求解梯度。
二、卷积层
2.1 动机:
对于一维
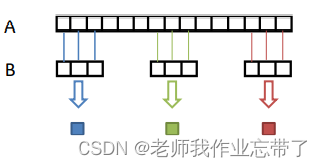
假设有A和B两个一维序列,其中B的长度小于A,计算B与A的每个部分之间的相似度(similarity)
自然地,将B在A上滑动并逐个计算相似度,简便起见,称为关联计算(correlation calculation)
𝑥 和 𝑦 两个向量间的余弦相似度(Cosine Similarity):
对于二维
同理假设A和B是两个二维序列,其中B的长宽小于A:
𝑥 和 𝑦 两个矩阵间的余弦相似度(Cosine Similarity):
注:得到的响应二维矩阵会比输入小一点,因此其3×3每次向右移动一小格取一次输出,且B始终在A里面,不出头。
但这个滑动的过程非常缓慢,为解决此问题,我们:
- 引入卷积和FFT(卷积和傅里叶变换)
- 使用并行计算(显卡)
当然引入卷积并不一定要非用FFT,当前使用并行计算更加流行也更快一些。
2.2 一维卷积
连续卷积:
离散卷积 (对于有限长的序列):

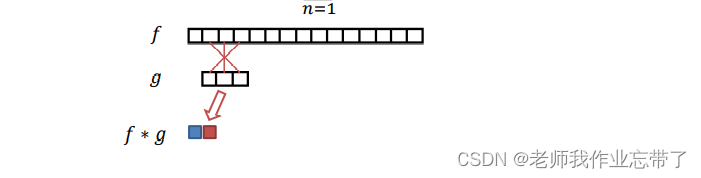
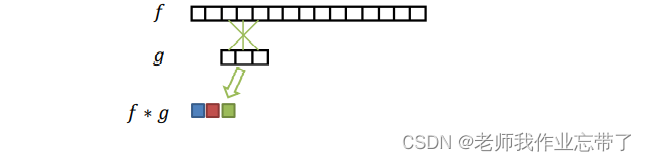
这与我们上面介绍的滑动相似度基本是一样的,不过本次是“交叉计算”。
三种卷积形式
𝑓的长度: 𝑀, 𝑔的长度: 𝑁, 其中 𝑀 ≥ 𝑁
- Valid卷积

- Full卷积

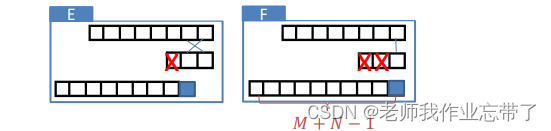
- Same卷积
将full卷积的结果截断至 𝑀 维
Same卷积也可以从 𝑔 与用零填充(zero-padded)的 𝑓 之间的Valid卷积得到
例如:
假设有两个序列:
f=[0,1,2,-1,3] g=[1,1,0]
则:
python代码:
import numpy as np from scipy import signal f = np.array([0, 1, 2, -1, 3]) g = np.array([1, 1, 0]) h1 = signal.convolve(f, g, mode='valid') h2 = signal.convolve(f, g, mode='full') h3 = signal.convolve(f, g, mode='same')
相似度和卷积之间的关系
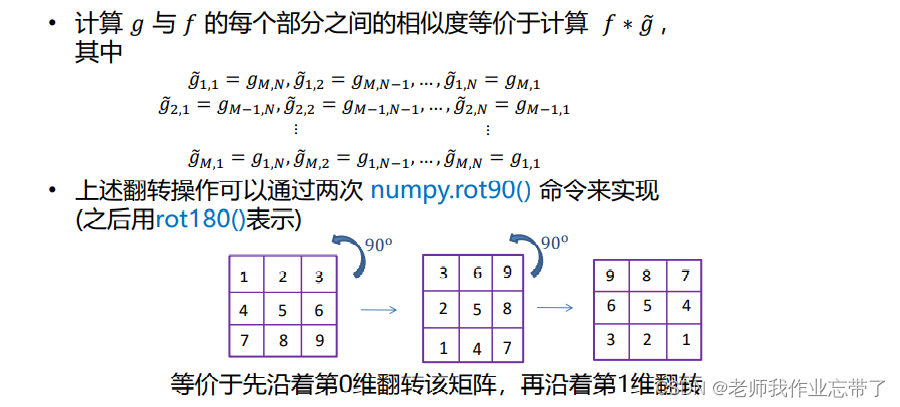
计算 𝑔 与 𝑓 的每个部分 之间的相似度等价于计算 𝑓 ∗ , 其中
也就是我们所谓的交叉计算
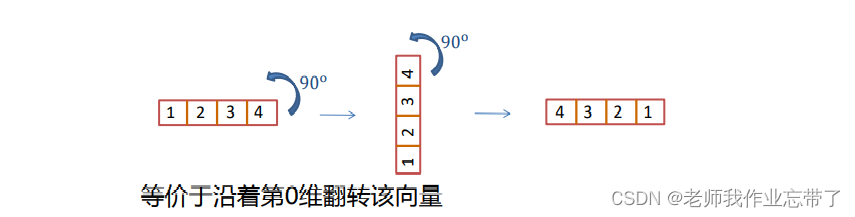
上述翻转操作可以通过两次 numpy.rot90() 命令来实现 (之后用rot180()表示)
2.3 二维卷积
假设有矩阵 𝑓 和 𝑔 , 大小分别 𝑀 × 𝑁 和 𝐾1 × 𝐾2, 其中 𝑀 ≥ 𝐾1, 𝑁 ≥ 𝐾2
两个矩阵间的离散卷积

- valid:h的大小是 (M-K1+1)*(N-K2+1)
- full:h的大小是 (M+K1-1)*(N+K2-1)
- same:h的大小是 M*N
python例子:
import numpy
from scipy import signal
A = numpy.array([[0, 0, 1, 2], [2, 2, 0, 0], [2, 1, 2, 2], [3, 0, 1, 1]])
B = numpy.array([[0, 0, -1], [1, -1, 1], [-1, 1, 1]])
C = signal.convolve2d(A, B, mode='full')
print(C)
C = signal.convolve2d(A, B, mode='valid')
print(C)
C = signal.convolve2d(A, B, mode='same')
print(C)
相似度和卷积之间的关系
同样是交叉计算,f 左上角对应 g 的右下角,g 的右上角对应 f 的左下角…
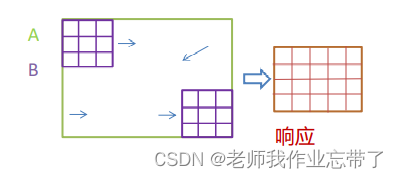
卷积核
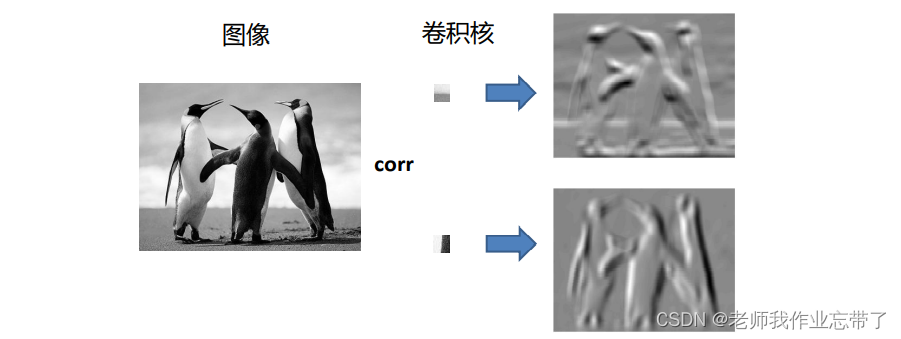
左侧输入图像就是A矩阵,卷积核B矩阵;
上图是对矩阵A和矩阵B进行相关联计算/似度计算,把卷积核B在A上滑动每个地方求一个响应。
ps:真正用卷积实现关联计算的话,应该先把卷积核翻转180°,再做卷积(因为卷积是交叉计算的),结果是一样的。相当于转了个弯,卷积:直接交叉计算,卷积表示关联计算:旋转再交叉计算。
特征图上的值越大(亮),表示图像上的该区域与卷积核的相似度越高。
此外:
我们可以看到第一种卷积核上面亮下面暗,第二种卷积核左边亮右边暗,则对应特征图上分体现出原图像上亮下暗,左亮右暗明显一些。
卷积可以节省参数量
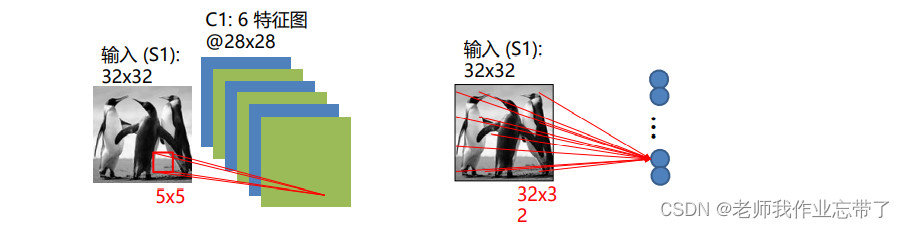
卷积:
- 每个特征图对应个25个参数
- 总参数量: 25 x 特征图数目(权值共享,6个卷积核)
全连:
- 每个神经元对应1024个参数
- 总参数量: 1024 x 神经元个数
扩展
- 使用same卷积保持特征图的空间尺寸不变
- 步长(stride)≠1的卷积操作
1. 保留空间尺寸
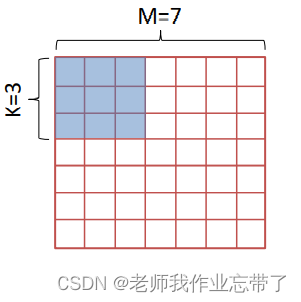
- 输入大小 M=7×7
- 卷积核大小 K=3×3
- 步长(stride)=1
- 输出大小 (valid模式): 5 * 5 (7-3+1)
下一次输入尺寸减小了 如 LeNet 5网络中的例子
如果不想减小输入尺寸,该怎么做?
一种方法是使用 same 卷积,但是有一些库不支持same卷积操作(前面介绍的只是python的操作,不是像tensorflow这样的操作),我们可以对valid进行填充0的操作:
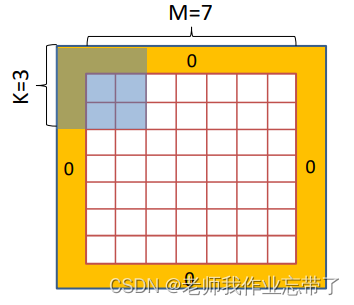
- 输入大小 M=7×7
- 卷积核大小 K=3×3
- 步长(stride)=1
- 在每处边缘填充一( (k-1)/2 )个像素
- 输出大小: 7×7 (same卷积)
通常我们选择K为奇数
为了保持输出尺寸与输入一致,当步长为1时,边缘应该填充多少?( (k-1)/2 )
2. 步长不为1的卷积
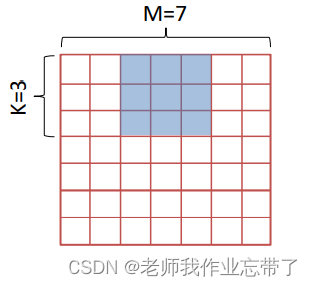
- 输入大小 M=7×7
- 卷积核大小 K=3×3
- 步长 stride=2
- 输出大小 (valid模式): 3×3
输出大小: (M-K)/stride+1
如果(M-K)/stride不是整数?
- 一般去掉多出来的部分,对结果影响不大。
- 说明网络的超参数设计不太对,设计M和K的时候不应该让它出现这种情况。
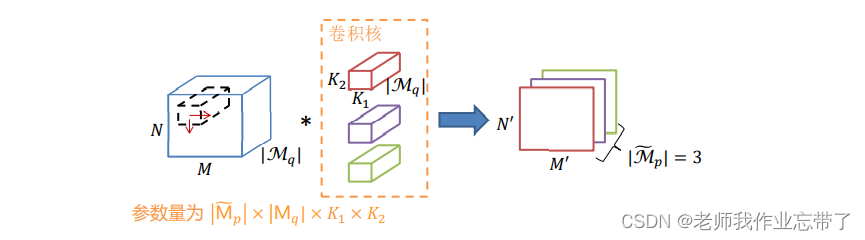
2.4 三维卷积
假设输入通道数与卷积核通道数一致
将三维输入中的一组二维特征图与卷积核对应的部分关联, 并对所有部分求和得到一组输出的特征图
— 可以通过翻转三维卷积核和三维卷积实现
三、池化层
3.1 池化介绍
下图8*10池化为2*2
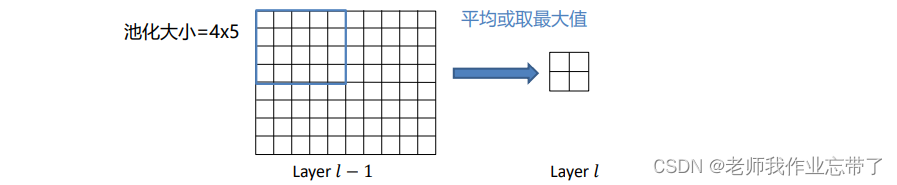
平均池化:
将卷积后的特征图划分为 𝑚 × 𝑛 个不相交区域,对每个区域分别进行取平均(或取最大值)操作,得到池化后的特征。在一维输入上的操作类似。
如果步长不等于池化大小怎么办?
说明是一种有重叠的池化
如何处理三维输入?
逐通道池化
3.2 为什么需要池化
减少分类中的特征数目
- 对于大小为96 × 96的输入图片. 如果有400组对应到8 × 8输入的特征, 则输出特征的大小为
增大下一层的感受区域
- 从池化结果中得到特征图会在像素空间中有更大的感受区域
不变性(invariance)
- 池化后的特征在局部区域内 拥有一定的平移不变性
类似于视觉神经元的感受野,其大小随视觉皮层层次的提高而增大。
3.3 卷积神经网络的组成与实现
组成
卷积层和池化层可以跟之前讨论的层组合使用
- 全连接层(Fully connected layer)
- Sigmoid层, ReLU层, 其它激活层
- 欧式损失层(Euclidean loss layer)
- 交叉熵损失层(Cross-entropy loss layer)
以及一些未讨论过的层,例如:
- 局部响应正则化 Local response normalization layer (Krizhevsky et al. 2012)
- 随机失活层 Dropout layer (Srivastava et al., 2014)
- 批正则化层 Batch normalization layer (Ioffe and Szegedy, 2015)
实现
- 将每个类型的层实现为一个类,并提供其前向和后向计算函数。
- 在主文件内通过指定层的类型来搭建卷积神经网络。
- 前向计算
- 计算输出
对所有的 𝑙 = 1,2, … , 𝐿。
- 计算输出
- 后向计算
- 计算
和
, 以及
对 𝑙 = 𝐿, 𝐿 − 1, … ,1。
- 计算
- 更新
和
对所有的 𝑙 = 1,2, … , L。
示例:
MNIST手写体数字识别 : ConvNetJS MNIST demo (stanford.edu)

CIFAR-10数据集分类: ConvNetJS CIFAR-10 demo (stanford.edu)

四、典型的卷积神经网络
LeNet-5
ImageNet挑战赛 (ILSVRC)

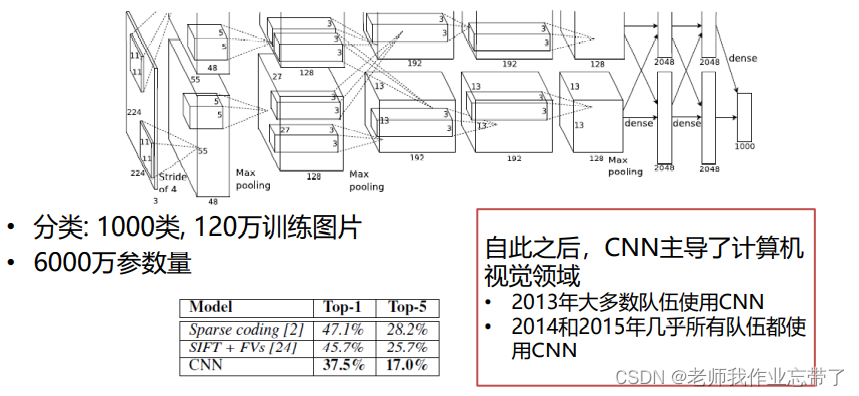
AlexNet
VGG net
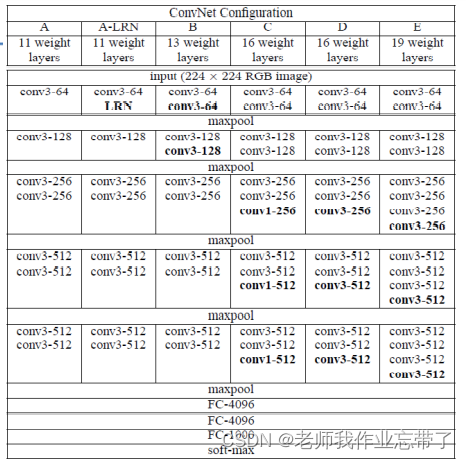
3*3 卷积核被广 泛使用,GPU实现。
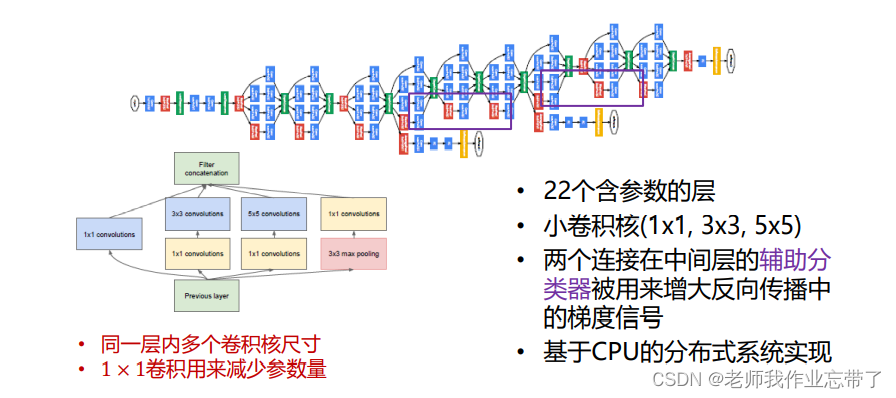
GoogLeNet (Inception-v1)
Inception-v2
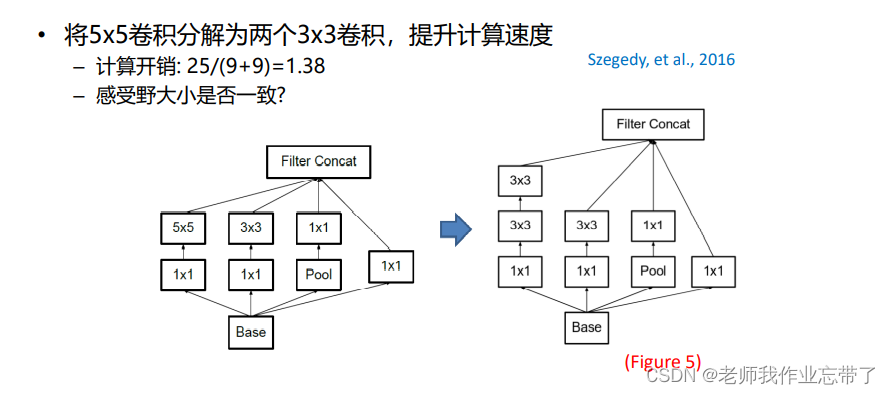
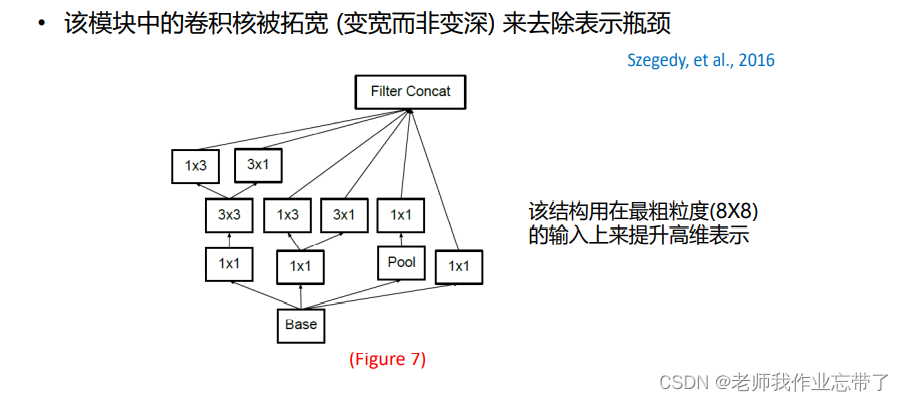
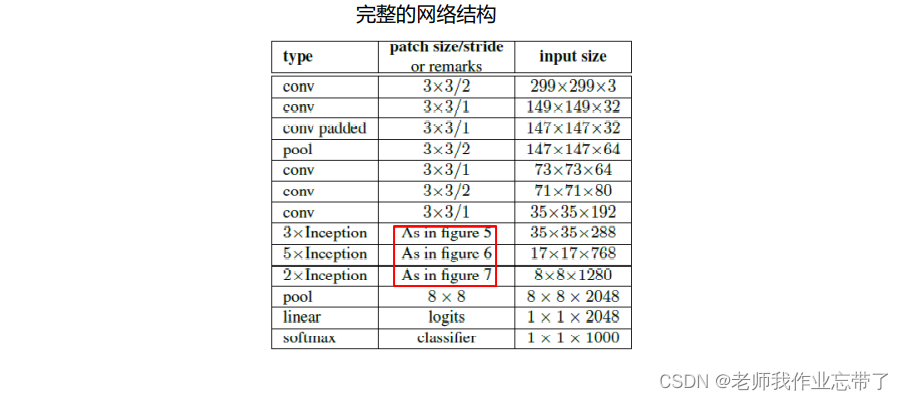
Inception-v3
在Inception-v2上添加额外的技术:
- RMSProp优化器.
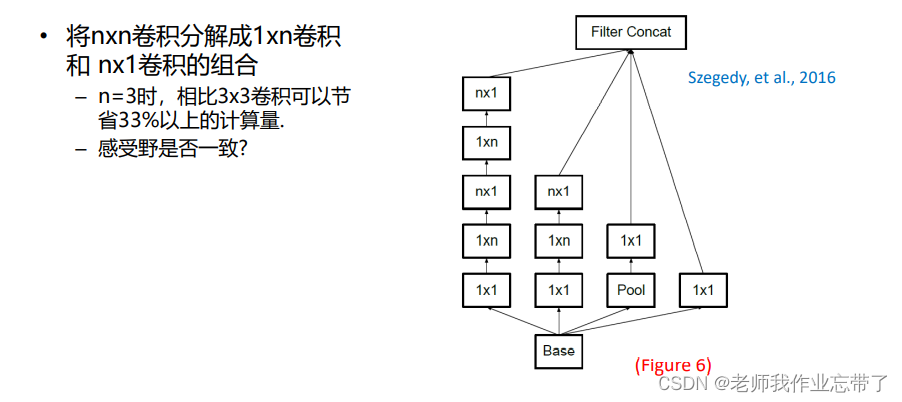
- 分解 7×7 卷积.
- 在辅助分类器中添加批归一化(BatchNorm)
- 标签平滑(Label Smoothing) (一种防止过拟合的正则化技术).
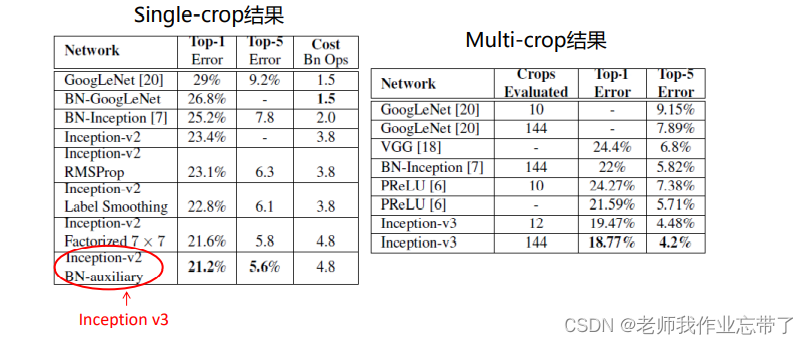
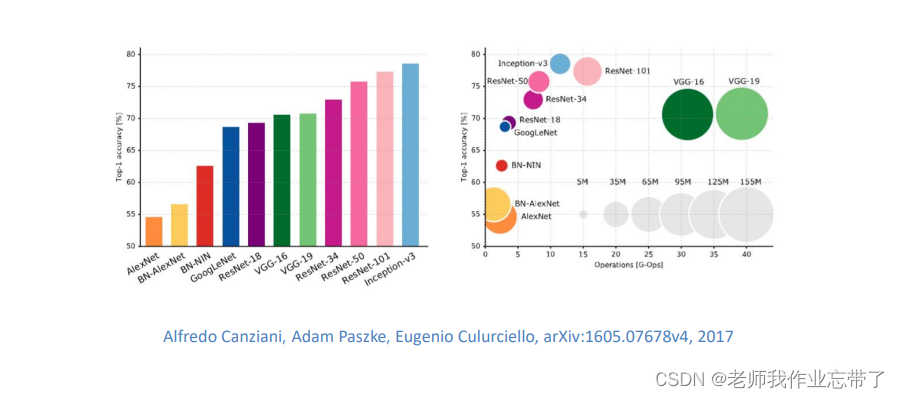
ImageNet数据集上的结果
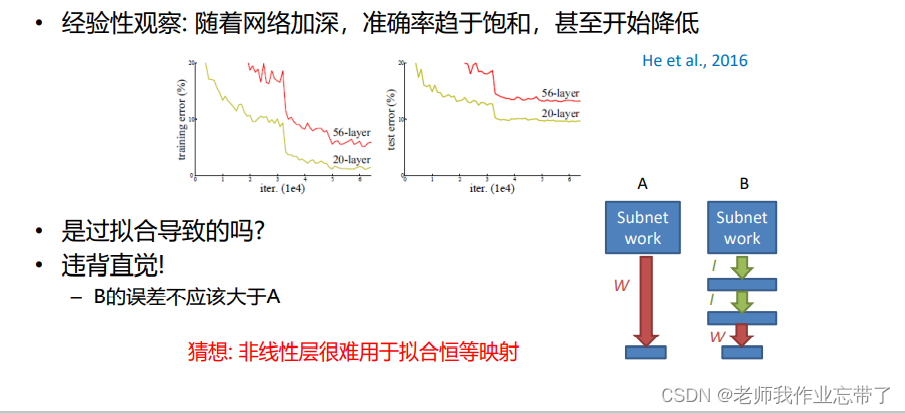
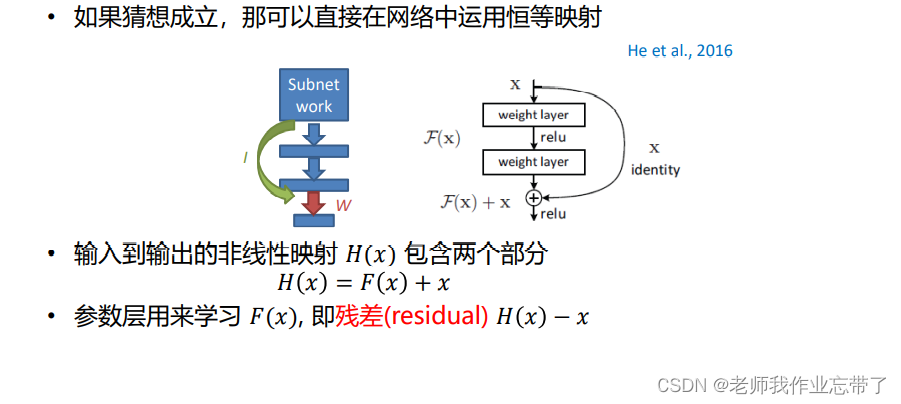
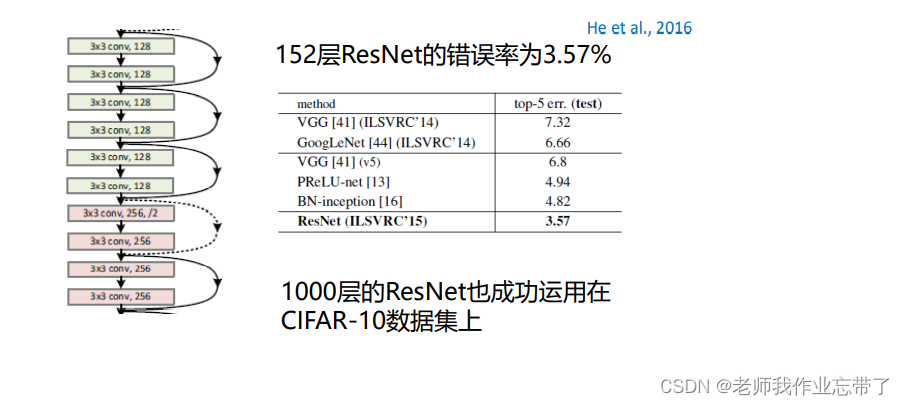
Deep residual network (ResNet)
DenseNet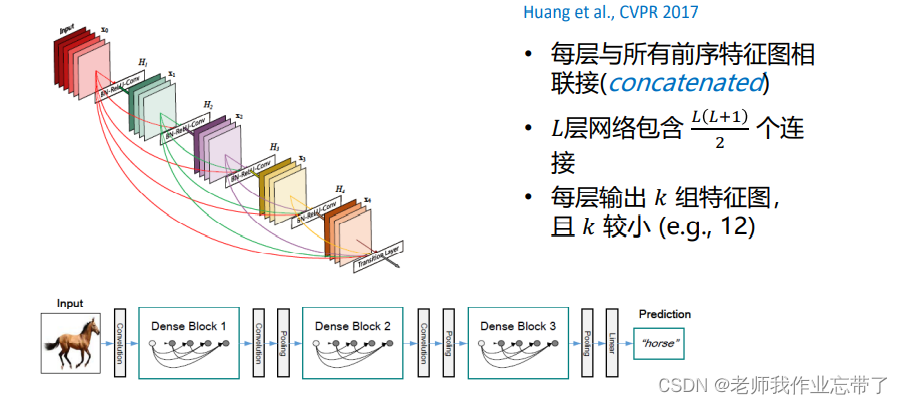
ImageNet数据集上的结果
文章出处登录后可见!