一、基本知识

1、模型的输入：

如果把输入看成一个向量，输出是数值或者类别。但是若输入是一系列的向量（序列），同时长度会改变，例如输入是一句英文，每个单词的长短不一，每个词汇对应一个向量，所以模型的输入是多个长短不一的向量集合，并且每个向量的大小都不一样。

另外有语音信号（其中一段语音为一个向量）、图论（每个节点是一个向量）也能描述为一串向量。

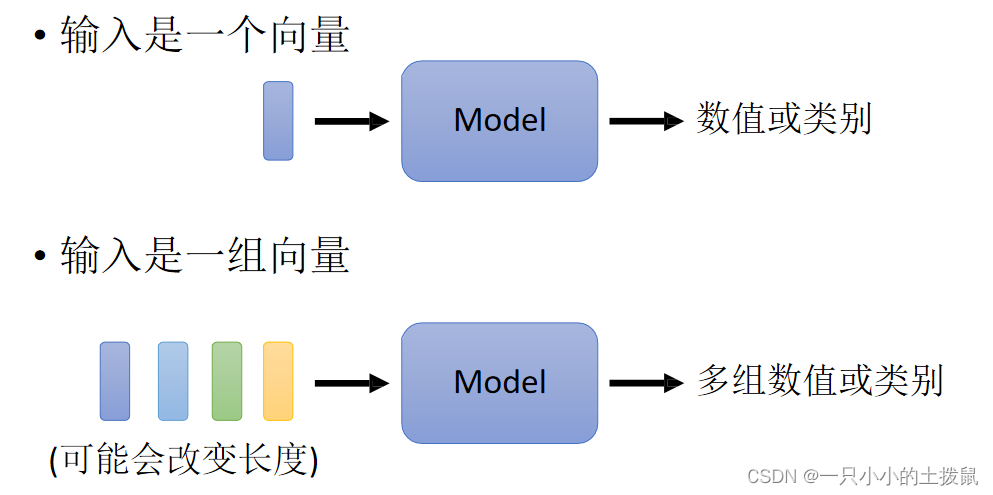
将单词表示为向量的方法，（1）可以利用one-hot encoding，向量的长度就是世界上所有词汇的数目，用不同位的1（其余位置为0）表示一个词汇，但是这种方式下每一个词之间没有关系，里面没有任何有意义的信息。（2）另一个方法是Word Embedding：给单词一个向量，这个向量有语义的信息，一个句子就是一排长度不一的向量。很显然这种方式下类别相同的词聚集在一起，因此它能区分出类别，将Word Embedding画出来：

自注意力机制要解决的问题是：当神经网络的输入是多个大小不一样的向量，并且可能因为不同向量之间有一定的关系，而在训练时却无法充分发挥这些关系，导致模型训练结果较差。

2、模型的输出：

（1）每个输入向量对应一个输出标签（Sequence Labeling）。例如，在文字处理时词性标注（每个输入的单词都输出对应的词性）。在社交网络中，推荐某个用户商品（可能会买或者不买）。

（2）多个输入向量对应一个输出标签。例如，对语义分析正面评价、负面评价。语音识别某人的音色。

（3）机器自己决定输出标签的个数 。例如，翻译语言A到语言B，单词字符数目不同。

3、一对一(Sequnce Labeling) 的情况：

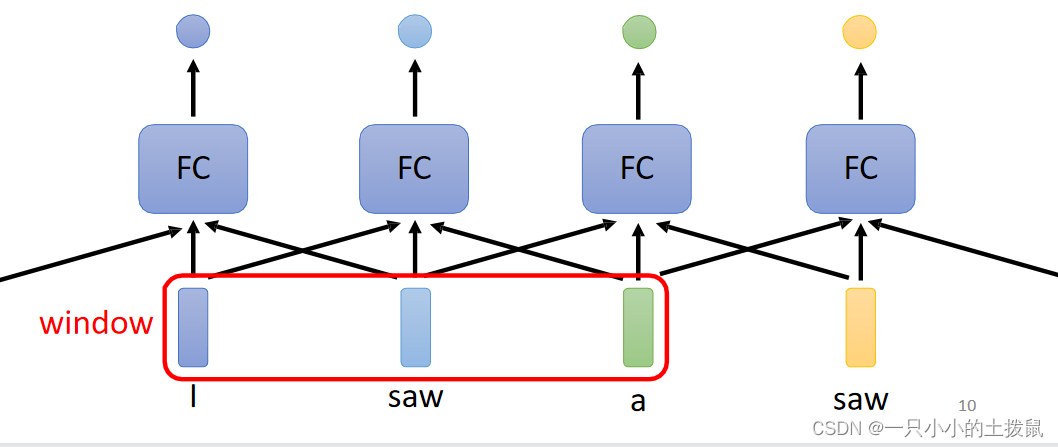
主要是上述第一种情况，每一个输入向量对应一个标签，这种情况又叫做Sequence Labeling。在一句话中如果有两个相同的字。可以使用一个window 滑动窗口，每个向量查看窗口中相邻的其他向量的性质，让FC考虑上下文判断它们的词性。但如果让一个window包括整个序列，但是这会让FC参数非常多，变得很复杂。 同时这种方法不能解决整条语句的分析问题，即语义分析。这就引出了 Self-attention 技术。

 二、Self-attention 自注意力机制

输入整个语句的向量到self-attention中，输出对应个数的向量，再将其结果输入到全连接网络，最后输出标签。过程可多次重复。

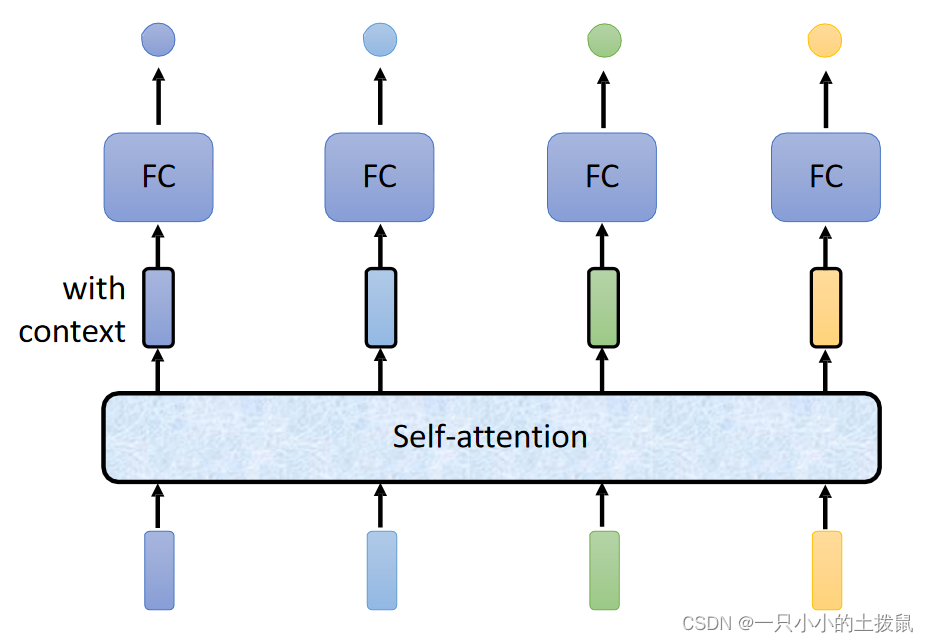
self-attention 最终得到的是：给定当前输入样本 （ 为了更好地理解，把输入进行拆解），产生一个输出，而这个输出是序列中所有样本的加权和。假设这个输出能看到所有输入的样本信息，然后根据不同权重选择自己的注意力点。本质上，对于每个输入向量，Self-Attention产生一个向量，该向量在其邻近向量上加权求和，其中权重由单词之间的关系或连通性决定。

 1、运行原理

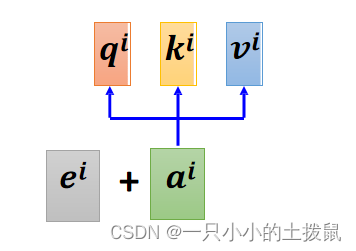
（1）这里需要三个向量：Query，Key，Value

假设  是一个输入样本序列的特征, 其中 n 为输入样本个数(序列长度)，d 是单个样本纬度。Query、Key & Value 定义如下：（X 、Q、K、V 的每一行代表一个输入样本）

Query：  ， 其中， 这个矩阵可以认为是空间变换矩阵，下同

Key：  ，其中

Value：  ，其中

其Q,K,V 的解释参考文章：如何理解 Transformer 中的 Query、Key 与 Value_yafee123的博客-CSDN博客_key query value

例如在推荐系统中，query 是某个人的喜好信息、key 是类型、value 是待推荐的物品。给定一个 query，计算query 与 key 的相关性，然后根据query 与 key 的相关性去找到最合适的 value。但是 self-attention 不是为了 query 去找 value，而是根据当前 query 获取 value 的加权和。

query, key 和 value 的每个属性虽然在不同的空间，其实他们是有一定的潜在关系的，一般来说，两个词向量的意思越接近，距离和夹角就越小，所以query, key 的乘积也会越大。通过某种变换，可以使得三者的属性在一个相近的空间中。

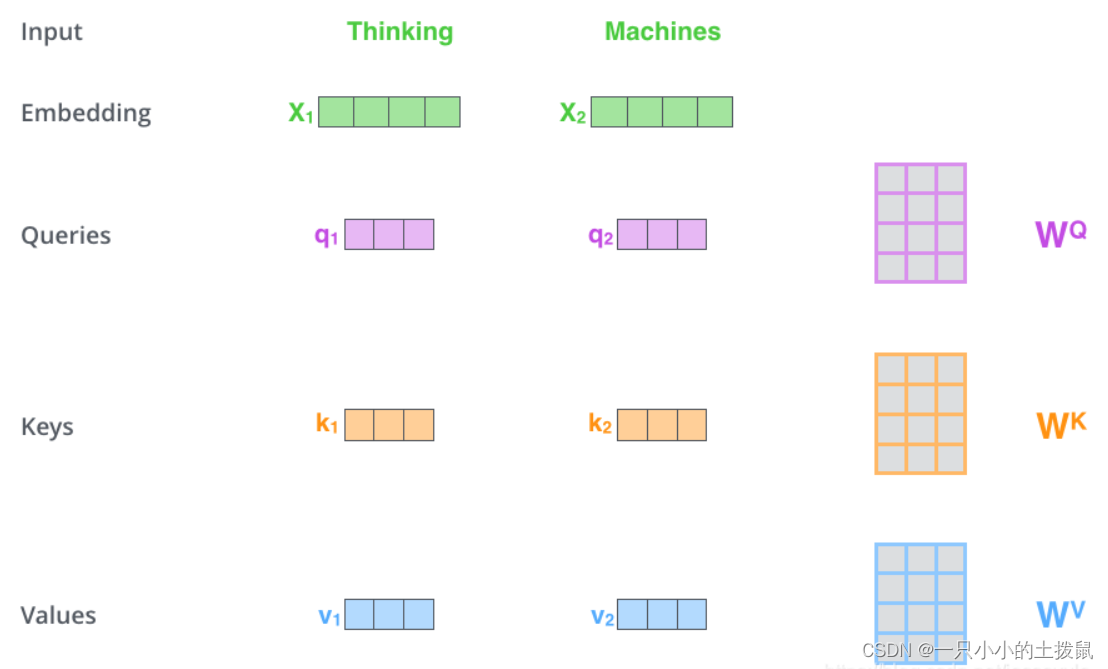
（2）Q,K,Y矩阵

在 self-attention 的原理中，当前的输入样本 ，通过空间变换变成了一个 query，  , 。

图中x1、x2就是句子中的一个个词向量，然后我们有三个矩阵：WQ、WK、WV，通过把词向量和这三个矩阵相乘，得到新的三个向量，这三个向量都是基于原先的词向量x生成的。

所谓的Q K V矩阵、查询向量之类的字眼，其来源都是 与矩阵的乘积，本质上都是 的线性变换。不直接使用 而要对其进行线性变换，是为了提升模型的拟合能力，矩阵 都是可以训练的，起到一个缓冲的效果。

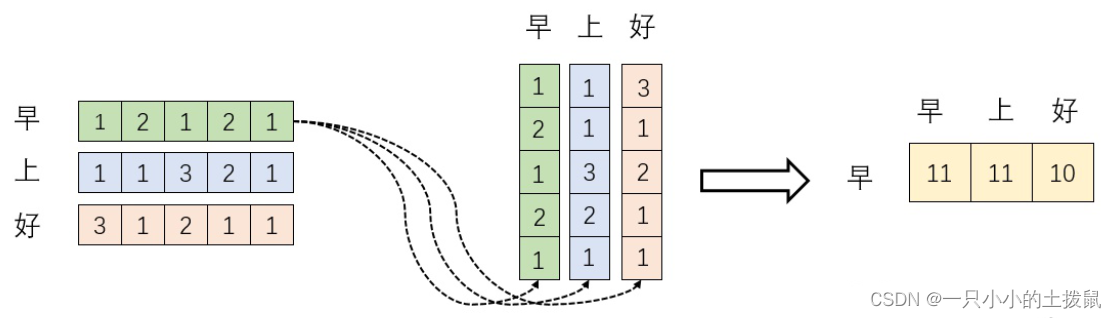
 （3） query 和key 相关性

下一步就是进行点积计算 query 和key 相关性，获得当前样本的关系向量α。向量内积的几何意义是表征两个向量的夹角，表征一个向量在另一个向量上的投影。投影值大，意味两个向量相关度高。如果两个向量夹角是90°，那么这两个向量线性无关，完全没有相关性。矩阵是一个方阵，以行向量的角度理解，里面保存了每个向量和自己与其他向量进行内积运算的结果。（11->0.4，11->0.4，10->0.2）

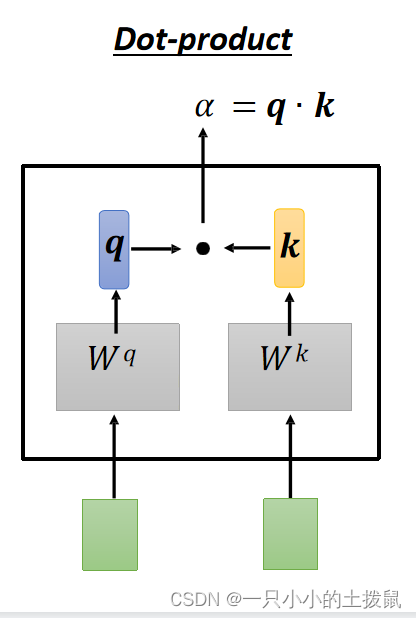
计算方法是两个向量作为输入，直接输出α。 这样，  中的每一个元素就可以看做是当前样本  与序列中其他样本之间的关系向量。类比于推荐中根据 query 与 key 的相关性去检索所需要的value。

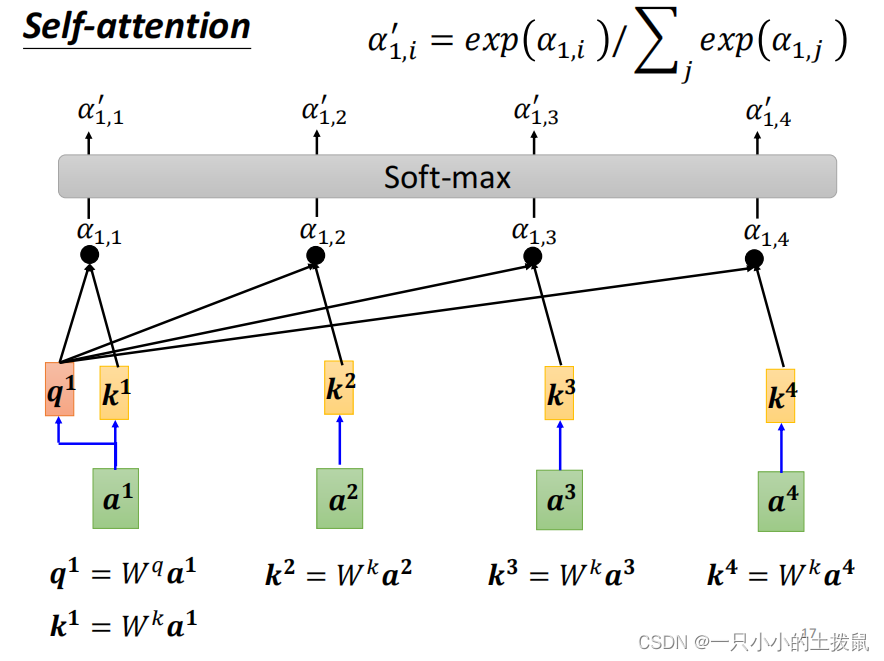
每一个相关的向量跟a1之间的关联程度用α来表示，分别计算出a1和每一个向量的关联性之后，也要计算和自己的关联性。下面的图片中的 ，，是向量a1和其他向量之间的关系向量。之后要做一个归一化 softmax 函数，也可以用relu等别的函数。那么权重就是这些归一化之后的数字。例如当关注“早”这个字的时候，分配0.4的注意力（attention）给它本身，剩下0.4的注意力给“上”，最后的0.2的注意力给“好”。

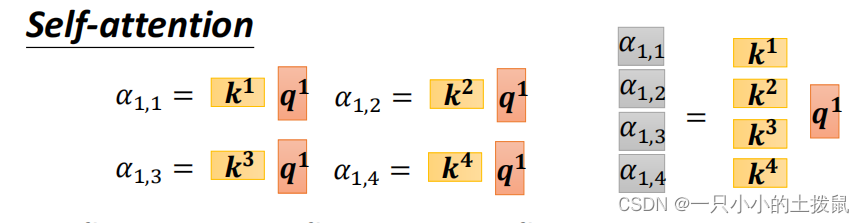
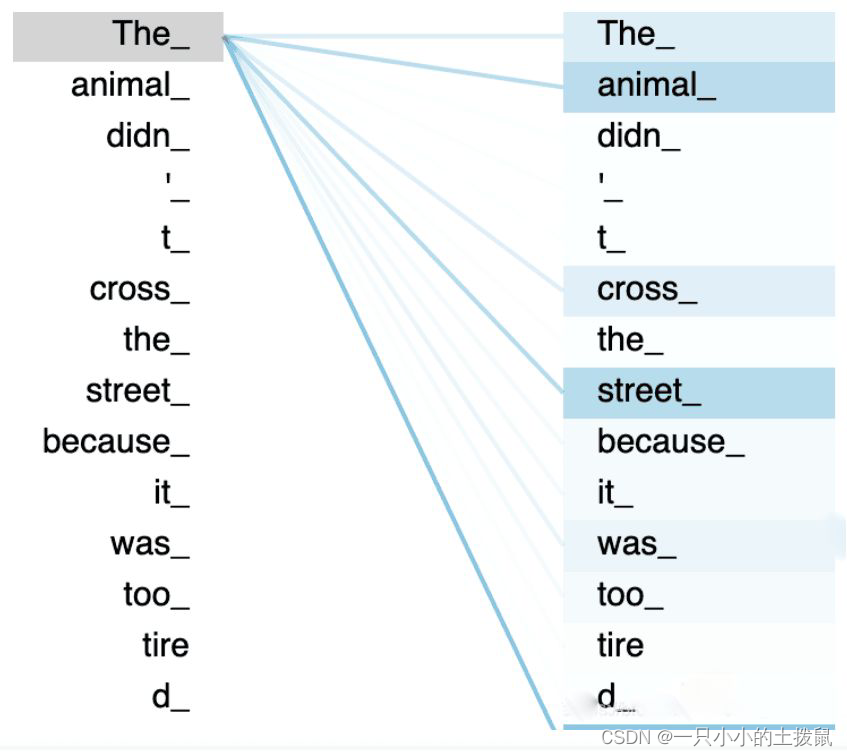
 一张更形象的图是这样的，图中右半部分的颜色深浅，其实就是上图中黄色向量中数值的大小，意义就是单词之间的相关度。

（4） 加权输出

得到样本之间的关联性 α‘ 之后，要根据关联性 α‘ 来抽取重要的信息，谁的关联性越强，谁的v就更影响结果。具体操作是每一个向量乘以一个新的权重矩阵W（v）得到新的向量，便可以得到self-attention 的最终加权输出。

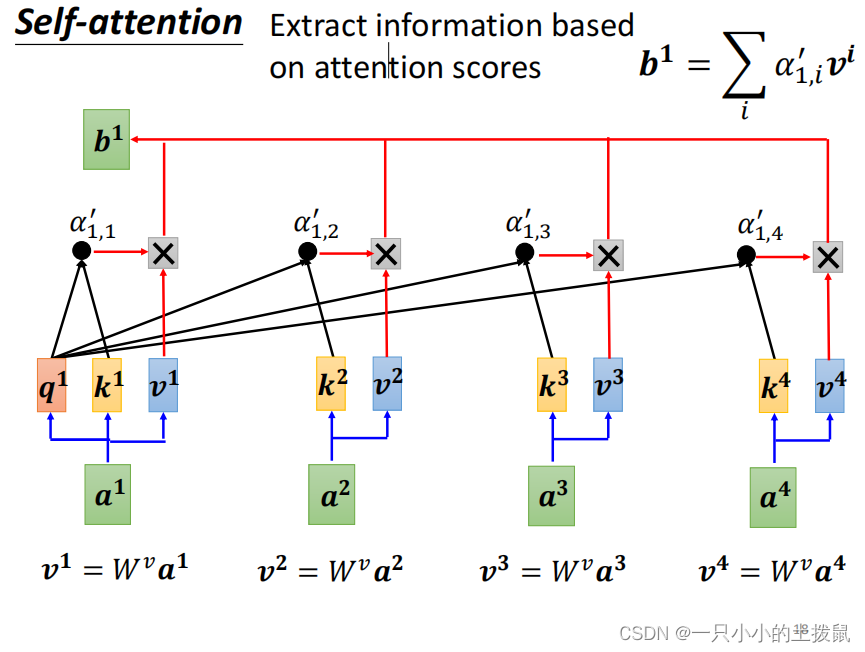
这个行向量与 的一个列向量相乘，得到一个新的行向量，且这个行向量与 的维度相同。 在新的向量中，每一个维度的数值都是由三个词向量在这一维度的数值加权求和得来的， 这个新的行向量就是"早"字词向量经过注意力机制加权求和之后的表示。

每一个原始向量只是一个代表一个单词的数字块。它对应的新向量 b 既表示原始单词，也表示它与周围其他单词的关系。  以此类推可以得到b2/b3/b4， 其中b i ( 1 ≤ i ≤ 4 ) 是同时计算出来的。

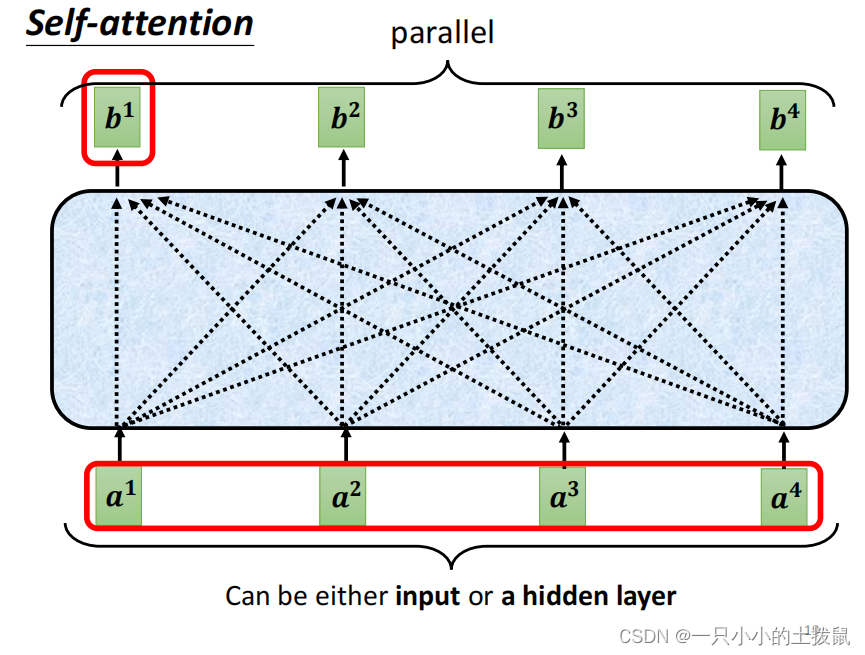
（5）将过程拼接起来

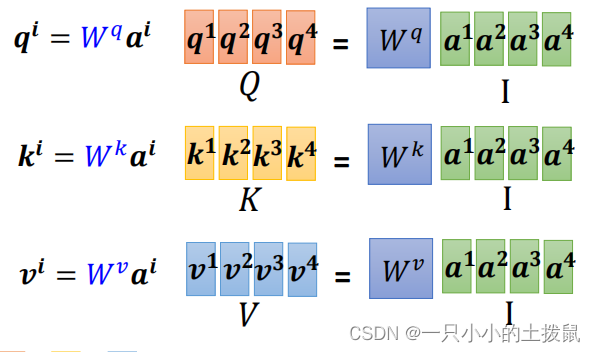
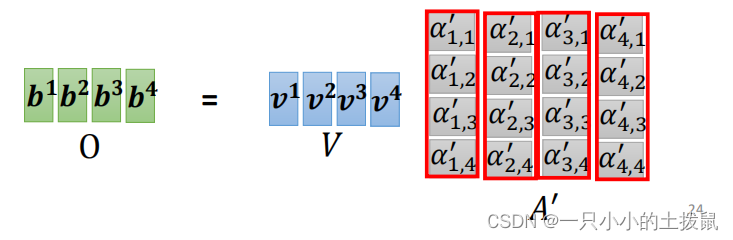
 （6）总结

• 输入矩阵 I 分别乘以三个 W 得到三个矩阵 Q , K , V 。
• 根据Query和Key计算两者的相似性或者相关性，进行归一化处理得到注意力矩阵
• 根据权重系数对Value进行加权求和，得到Attention Value，输出， 其中 O 的每一维输出，相当于是所有输入序列样本对应纬度的加权和，而权重就是关系向量  
• ，其中为向量的长度。

的意义：维度较大时，向量内积容易使得 SoftMax 将概率全部分配给最大值对应的 Label，其他 Label 的概率几乎为 0，反向传播时这些梯度会变得很小甚至为 0，导致无法更新参数。因此，一般会对其进行缩放，缩放值一般使用维度 dk 开根号，是因为点积的方差是 dk，缩放后点积的方差为常数 1，这样就可以避免梯度消失问题。d的维度就是QK的维度，除以d的目的就是降低方差 。

假设 Q, K 都服从均值为0，方差为1的标准高斯分布，那么中元素的均值为0，方差为d。当d变得很大时， A中的元素的方差也会变得很大，那么 Softmax(A)的分布会趋于陡峭（分布方差大，分布集中在绝对值大的区域）。

总结一下就是 Softmax(A)的分布会和d有关。因此A中每个元素除以后，方差又变为了1。这使得Softmax(A)的分布的陡峭程度和d成功解耦，从而使得Transformer在训练过程中的梯度值保持稳定。

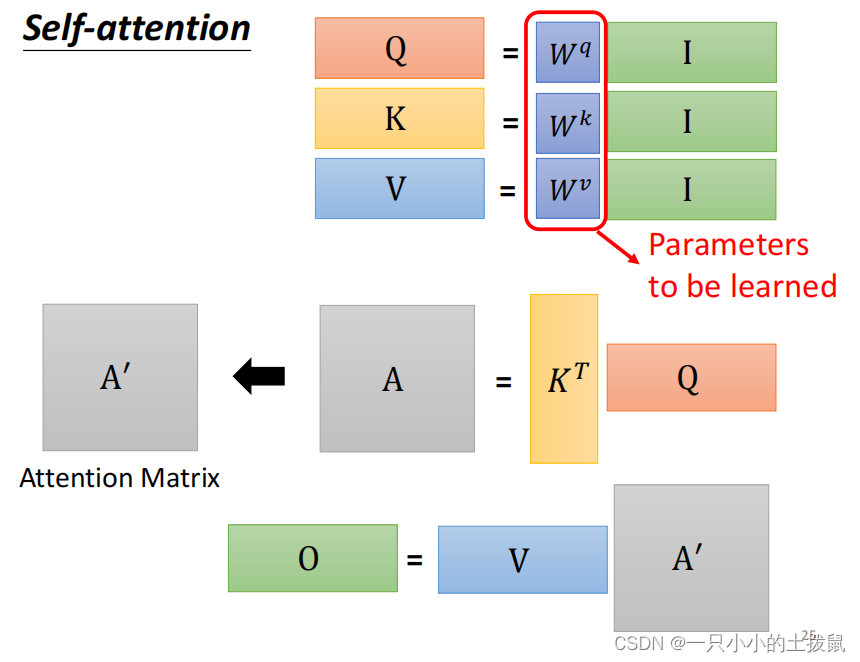
其中唯一要训练出的参数就是 W， 具体计算：动手推导Self-Attention

2. 多头注意力机制 (Multi-head Self-attention)

 上述的self-attention中，每个输入特征 乘上矩阵 后，分别得到一个向量 ，称为单头自注意力机制。如果将这些向量分裂为 n 个就得到 n 头自注意力机制了。每次Q,K,V运算为一个头，公认多头自注意力机制的效果好于单头的，因为前者可以捕获更多维度的信息。示意图如下：

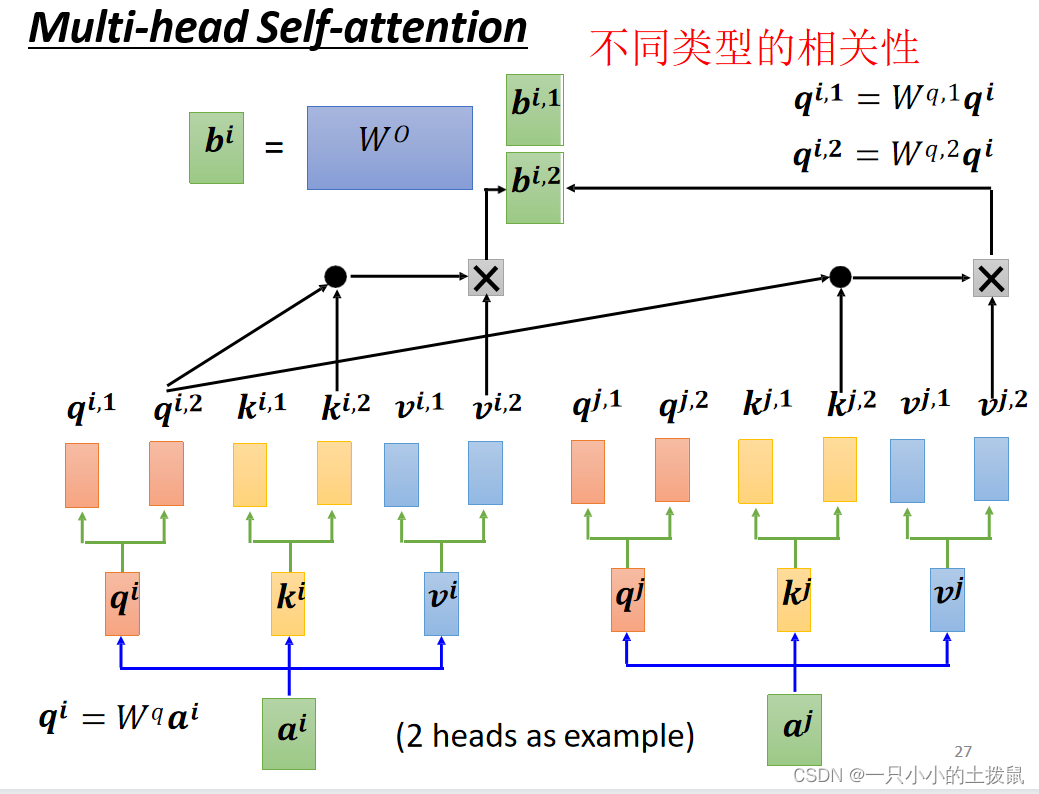
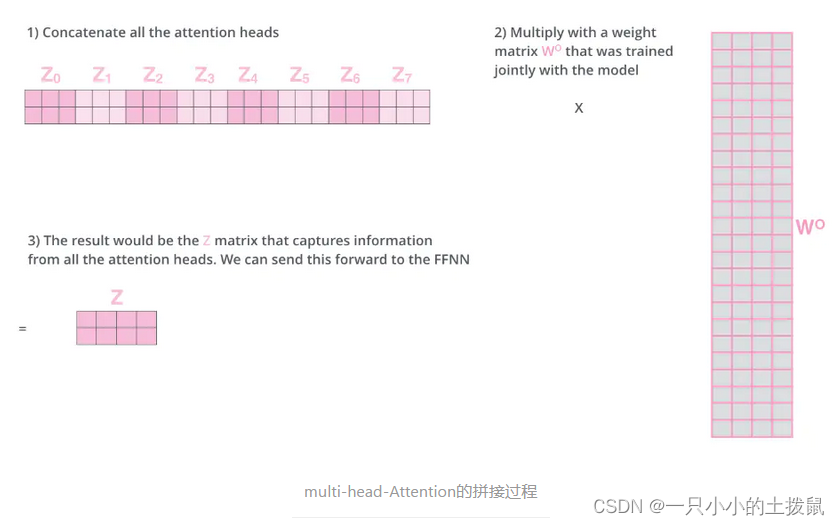
具体操作过程是：输入还是 Query，Key，Value，首先经过一个线性变换，然后输入到attention中，注意这里要做 n 次，其实也就是所谓的多头，每一次算一个头。而且对每一个head，Q，K，V进行线性变换的参数 W 是不一样的（）。然后将 n 次的放缩点积attention的结果进行拼接，再进行一次线性变换得到的值作为多头attention的结果。最终输出变成了不同head的输出的拼接结果。

transformer模型中的self-attention和multi-head-attention机制_小镇大爱的博客-CSDN博客_multihead self-attention

可以看到，一个self-attention会输出一个结果z。那么，multi-head-attention的输出是把每一个self-attention的输出结果拼接起来。然后输入给后面的全连接网络。多头attention的不同之处在于进行了h次计算而不仅仅算一次，这样的好处是可以允许模型在不同的表示子空间里学习到相关的信息。

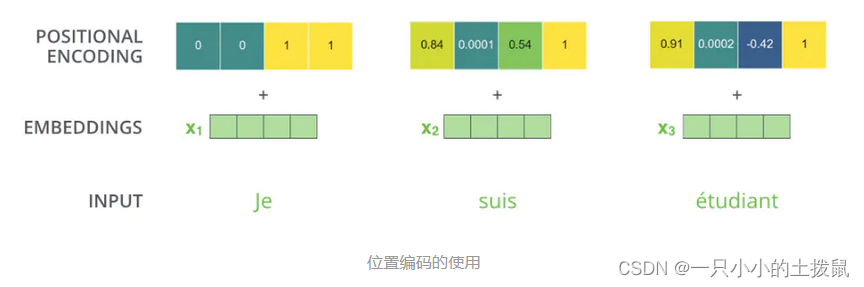
3. 位置编码 (Positional Encoding)

每一个不同的位置都有一个专属的向量 ，然后再做 的操作即可。但是这个  是人工标注的，就会出现很多问题：在确定 的时候只定到128，但是序列长度是129。

Transformer模型并没有捕捉顺序序列的能力，也就是说无论句子的结构怎么打乱，Transformer都会得到类似的结果。为了解决这个问题，在编码词向量时引入了位置编码（Position Embedding）的特征。具体地说，位置编码会在词向量中加入了单词的位置信息，这样Transformer就能区分不同位置的单词了。使用的用三角函数编码的方法。具体公式如下 ：

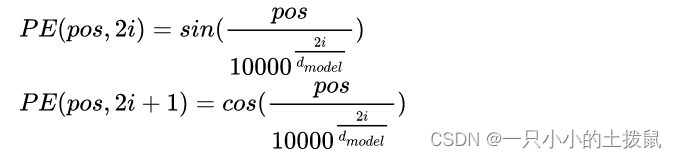
这里的pos表示单词的位置， i表示embedding的维度。之所以用sin, cos 是因为它们的值域在[-1, 1]之间,  这里针对单个词向量内部采用cos 和sin 交换映射, 只是为了丰富位置信息。

Position Embedding 本身是一个绝对位置的信息，但在语言中，相对位置也很重要，上述的位置向量公式的一个重要原因如下：除了单词的绝对位置，单词的相对位置也非常重要。由于我们有 sin(α+β)=sinα cosβ+cosα sinβ 以及 cos(α+β)=cosα cosβ−sinα sinβ，这表明位置 p+k 的向量可以表明位置 p 的向量的线性变换，这提供了表达相对位置信息的可能性。（其实我也看不懂）

 三、自注意力机制的其他应用

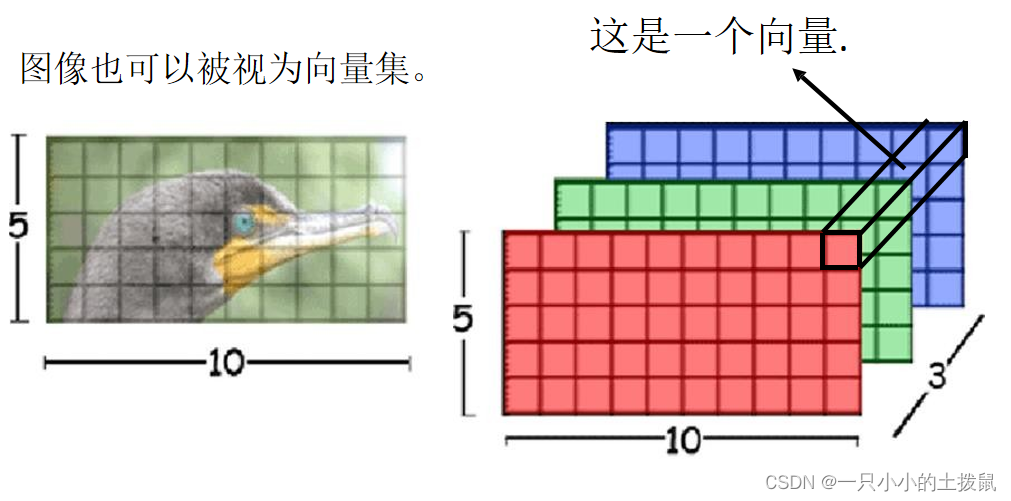
1、图像识别

在做CNN的时候，一张图片可看做一个很长的向量。它也可看做 一组向量：一张 5 ∗ 10 的RGB图像可以看做 5 ∗ 10 的三个（通道）矩阵，把三个通道的相同位置看做一个三维向量。

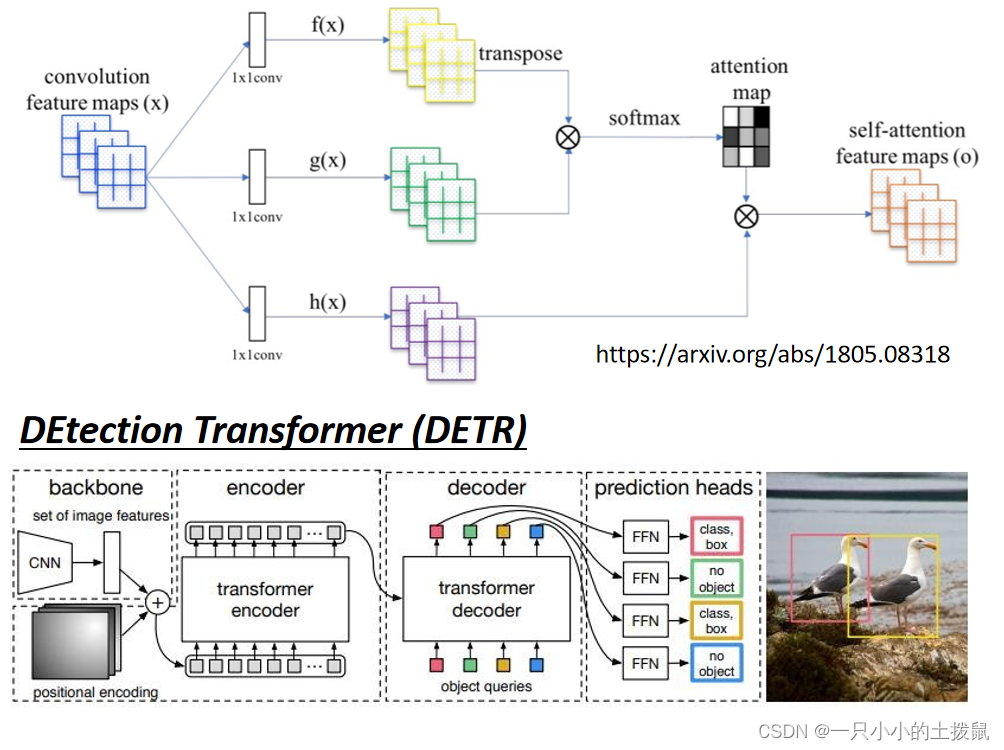
 具体应用：GAN（生成对抗网络）、DETR

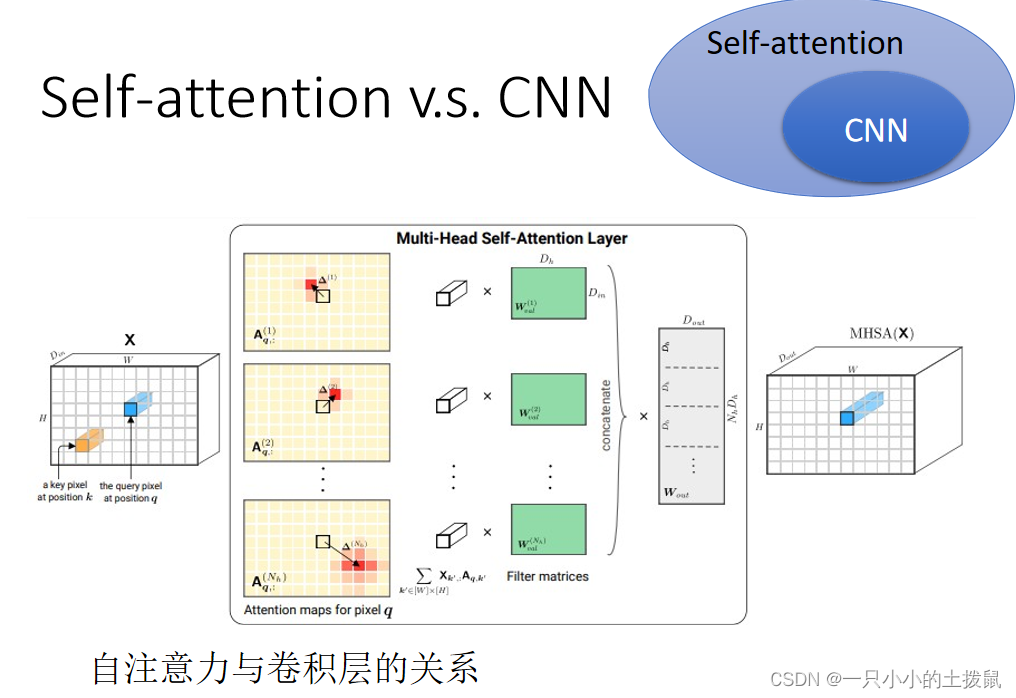
 （1）自注意力机制和CNN的差异

• CNN看做简化版的self-attention：CNN只考虑一个感受野里的信息，self-attention考虑整张图片的信息
• self-attention是复杂版的CNN：CNN里面每个神经元只考虑一个感受野，其范围和大小是人工设定的；自注意力机制中，用attention去找出相关的像素，感受野就如同自动学出来的。

 如果用不同的数据量来训练CNN和self-attention，会出现不同的结果。大的模型self-attention如果用于少量数据，容易出现过拟合；而小的模型CNN，在少量数据集上不容易出现过拟合。

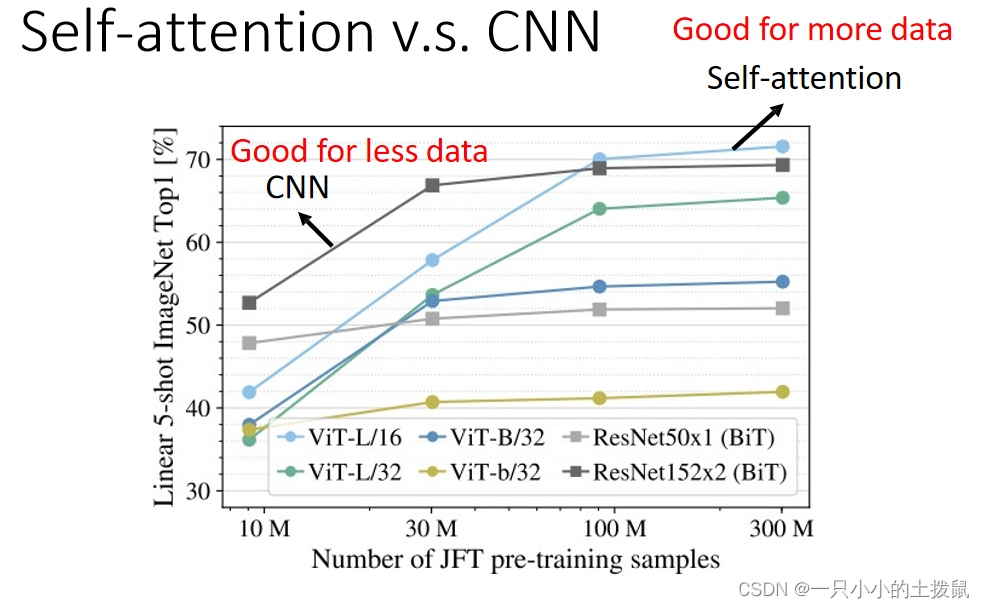
 参考文献：李宏毅《深度学习》- Self-attention 自注意力机制_Beta Lemon的博客-CSDN博客_自注意力模型