前言
最近一直在做类ChatGPT项目的部署 微调,关注比较多的是两个:一个LLaMA,一个ChatGLM,会发现有不少模型是基于这两个模型去做微调的,说到微调,那具体怎么微调呢,因此又详细了解了一下微调代码,发现微调LLM时一般都会用到Hugging face实现的Transformers库的Trainer类
从而发现,如果大家想从零复现ChatGPT,便得从实现Transformer开始,因此便开启了本文:如何从零起步实现Transformer、ChatGLM(至于LLaMA已在之前的博客里解读过),主要分为两个大部分
- 按照Transformer每一步的原理逐步逐行从零实现(主要参考harvard对transformer的实现),先编码器后解码器,特别是注意力机制(缩放点积、多头注意力)
- 从头到尾解读ChatGLM-6B的整体代码架构,及逐行解读每一行代码
且本文的代码解读与其他代码解读最大的不同是:会对出现在本文的每一行代码都加以注释、解释、说明,甚至对每行代码中的变量都会做解释/说明
总之,一如既往的保持对初学者的足够友好,让即便没有太多背景知识的也能顺畅理解本文
第一部分 从零实现Transformer编码器模块
transformer强大到什么程度呢,基本是17年之后绝大部分有影响力模型的基础架构都基于的transformer(比如,这里有200来个,包括且不限于基于decode的GPT、基于encode的BERT、基于encode-decode的T5等等)
通过博客内的这篇文章《Transformer通俗笔记:从Word2Vec、Seq2Seq逐步理解到GPT、BERT》,我们已经详细了解了transformer的原理(如果忘了,建议必复习下再看本文,当然,如果你实在不想跳转,就只想呆在本文,也行,我努力..)
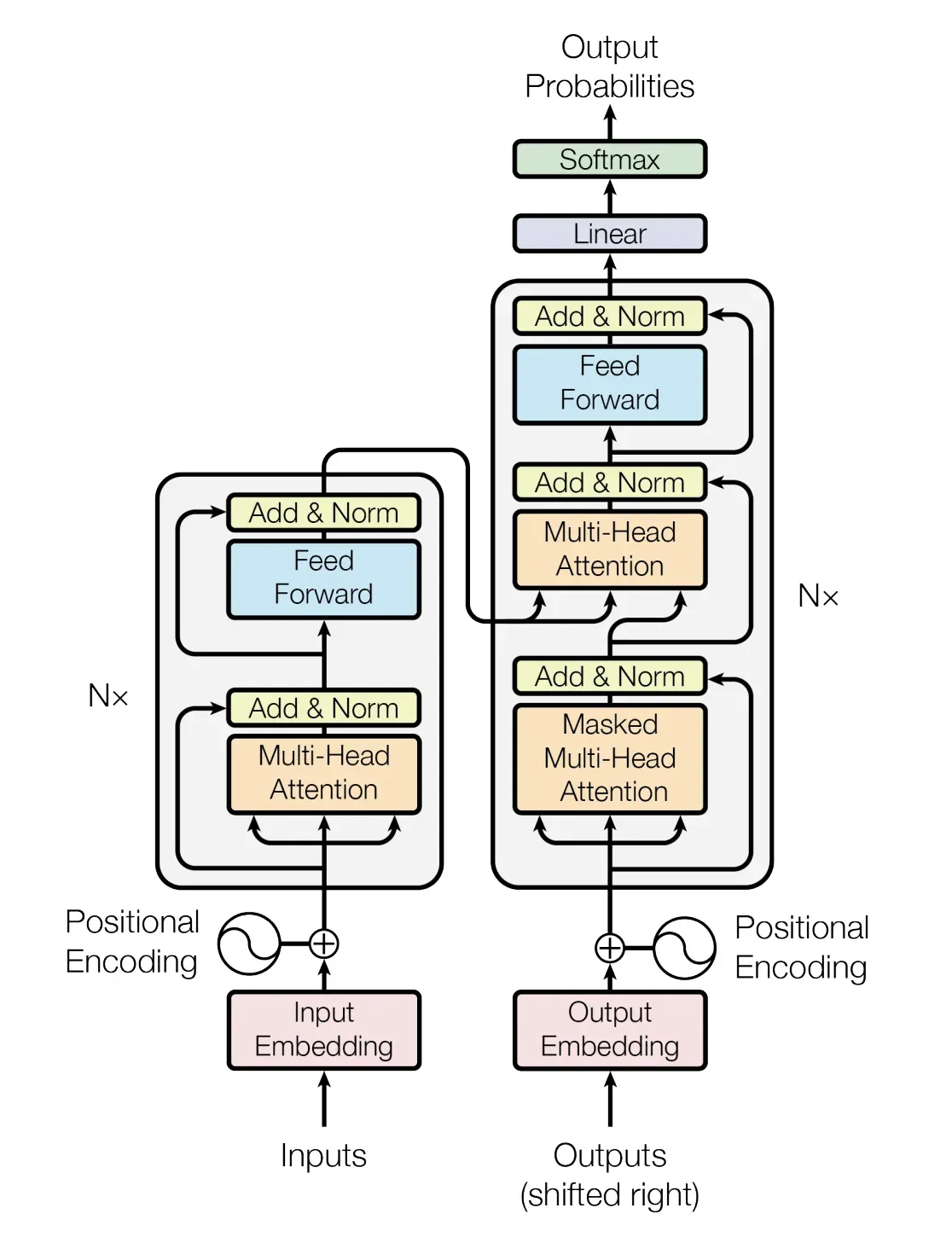
如果把上图中的各种细节也显示出来,则如下大图所示(此大图来源于七月在线NLP11里倪老师讲的Transformer模型源码解读,positional encoding、多头等没画)
具体说来,是一个典型的编码器-解码器架构
# 定义一个基于 nn.Module 的编码器-解码器类
class EncoderDecoder(nn.Module):
# 初始化方法,接收编码器、解码器、源嵌入、目标嵌入和生成器作为参数
def __init__(self, encoder, decoder, src_embed, tgt_embed, generator):
# 调用 nn.Module 的初始化方法
super(EncoderDecoder, self).__init__()
self.encoder = encoder # 将传入的编码器实例保存为类属性
self.decoder = decoder # 将传入的解码器实例保存为类属性
self.src_embed = src_embed # 将传入的源嵌入实例保存为类属性
self.tgt_embed = tgt_embed # 将传入的目标嵌入实例保存为类属性
self.generator = generator # 将传入的生成器实例保存为类属性
# 前向传播方法,接收源序列、目标序列和它们的掩码作为参数
def forward(self, src, tgt, src_mask, tgt_mask):
# 对源序列进行编码,并将编码结果与掩码传递给解码器进行解码
return self.decode(self.encode(src, src_mask), src_mask,
tgt, tgt_mask)
# 编码方法,接收源序列和掩码作为参数
def encode(self, src, src_mask):
# 将源序列进行嵌入,然后将嵌入后的序列和源序列掩码传给编码器
return self.encoder(self.src_embed(src), src_mask)
# 解码方法,接收编码器输出(memory)、源序列掩码、目标序列和目标序列掩码作为参数
def decode(self, memory, src_mask, tgt, tgt_mask):
# 将目标序列进行嵌入,然后将嵌入后的序列、编码器输出、源序列掩码和目标序列掩码传给解码器
return self.decoder(self.tgt_embed(tgt), memory, src_mask, tgt_mask)
# 定义一个基于 nn.Module 的生成器类
class Generator(nn.Module):
# 初始化方法,接收模型维度(d_model)和词汇表大小(vocab)作为参数
def __init__(self, d_model, vocab):
# 调用 nn.Module 的初始化方法
super(Generator, self).__init__()
# 定义一个线性层,将模型的输出维度映射到词汇表大小
self.proj = nn.Linear(d_model, vocab)
# 前向传播方法,接收输入 x
def forward(self, x):
# 将输入 x 传入线性层,然后对输出应用 log-softmax 激活函数(在最后一个维度上)
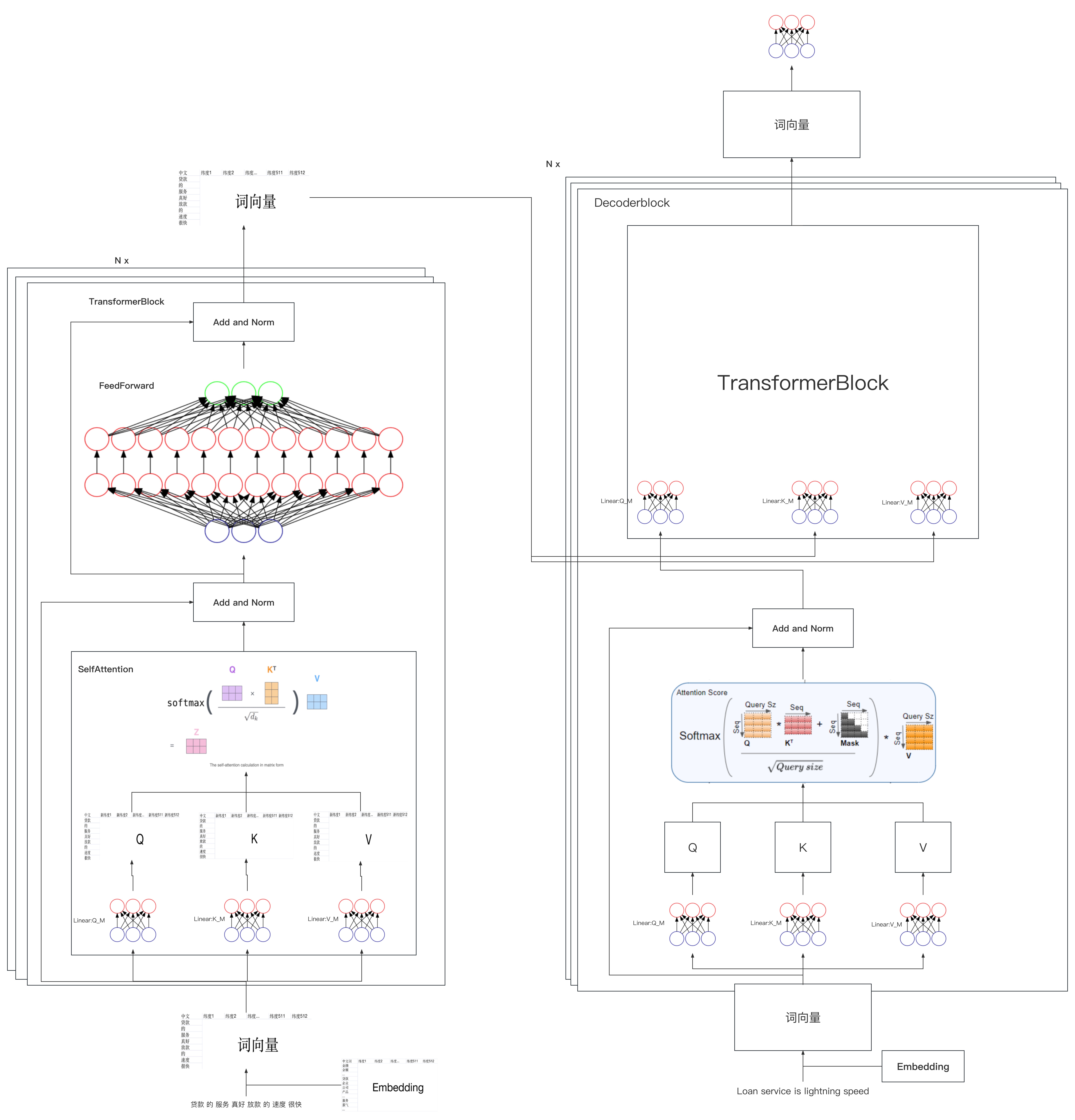
return F.log_softmax(self.proj(x), dim=-1)考虑到Hugging face实现的Transformers库虽然功能强大,但3000多行,对于初次实现的初学者来说,理解难度比较大,因此,咱们一步步结合对应的原理来逐行编码实现一个简易版的transformer
1.1 关于输入的处理:针对输入做embedding,然后加上位置编码
为了方便后面代码的编写,先引入一些库
import numpy as np # 导入NumPy库,用于进行矩阵运算和数据处理
import torch # 导入PyTorch库,用于构建神经网络及相关操作
import torch.nn as nn # 导入PyTorch神经网络模块,用于构建神经网络层
import torch.nn.functional as F # 导入PyTorch神经网络函数库,用于激活函数、损失函数等
import math, copy, time # 导入数学库、复制库和时间库,用于各种数学计算、复制操作和计时
from torch.autograd import Variable # 从PyTorch自动微分库中导入Variable类,用于构建自动微分计算图
import matplotlib.pyplot as plt # 导入Matplotlib的pyplot模块,用于绘制图表和可视化
import seaborn # 导入Seaborn库,用于绘制统计图形和美化图表
seaborn.set_context(context="talk") # 设置Seaborn的上下文环境,设置图表的尺寸和标签字体大小等
%matplotlib inline # IPython魔术命令,使Matplotlib绘制的图形直接显示在Notebook内1.1.1 针对输入做embedding
对于模型来说,每一句话比如“七月的服务真好,答疑的速度很快”,在模型中都是一个词向量,但如果每句话都临时抱佛脚去生成对应的词向量,则处理起来无疑会费时费力,所以在实际应用中,我们会事先预训练好各种embedding矩阵,这些embedding矩阵包含常用领域常用单词的向量化表示,且提前做好分词
| 维度1 | 维度2 | 维度3 | 维度4 | … | 维度512 |
| 教育 | |||||
| 机构 | |||||
| 在线 | |||||
| 课程 | |||||
| .. | |||||
| 服务 | |||||
| 答疑 | |||||
| 老师 |
从而当模型接收到“七月的服务真好,答疑的速度很快”这句输入时,便可以从对应的embedding矩阵里查找对应的词向量,最终把整句输入转换成对应的向量表示
这部分的代码 可以如下表示
# 定义一个名为Embeddings的类,继承自PyTorch的nn.Module类
class Embeddings(nn.Module):
# 初始化Embeddings类
def __init__(self, d_model, vocab):
# 调用父类nn.Module的初始化方法
super(Embeddings, self).__init__()
# 创建一个词嵌入层,参数为词汇表大小和词嵌入维度
self.lut = nn.Embedding(vocab, d_model)
# 将词嵌入维度保存为类属性
self.d_model = d_model
# 定义前向传播方法
def forward(self, x):
# 通过词嵌入层将输入的单词编码为向量,并乘以词嵌入维度的平方根进行缩放
return self.lut(x) * math.sqrt(self.d_model)1.1.2 位置编码的深意:如何编码更好
然,如此篇文章所述,RNN的结构包含了序列的时序信息,而Transformer却完全把时序信息给丢掉了,比如“他欠我100万”,和“我欠他100万”,两者的意思千差万别,故为了解决时序的问题,Transformer的作者用了一个绝妙的办法:位置编码(Positional Encoding)。
即将每个位置编号,从而每个编号对应一个向量,最终通过结合位置向量和词向量,作为输入embedding,就给每个词都引入了一定的位置信息,这样Attention就可以分辨出不同位置的词了,具体怎么做呢?
- 如果简单粗暴的话,直接给每个向量分配一个数字,比如1到1000之间
- 也可以用one-hot编码表示位置

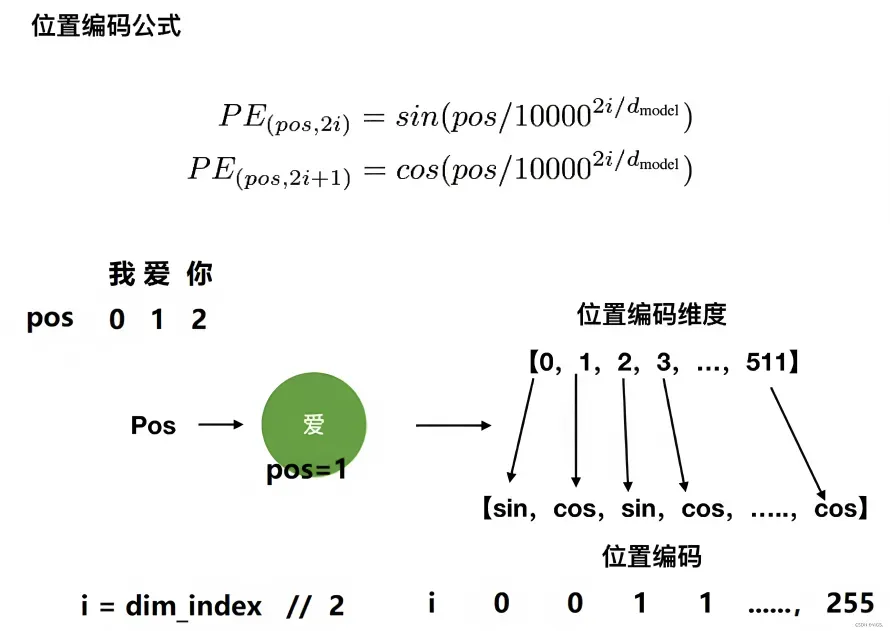
- transformer论文中作者通过sin函数和cos函数交替来创建 positional encoding,其计算positional encoding的公式如下
其中,pos相当于是每个token在整个序列中的位置,相当于是0, 1, 2, 3…(看序列长度是多大,比如10,比如100),代表位置向量的维度(也是词embedding的维度,transformer论文中设置的512维)
至于
相当于是embedding向量的位置下标对2求商并取整(可用双斜杠
表示整数除法,即求商并取整),它的取值范围是
,比如
,
,
,
,
,
,
…,
,
是指向量维度中的偶数维,即第0维、第2维、第4维…,第510维,用sin函数计算
是向量维度中的奇数维,即第1维、第3维、第5维..,第511维,用cos函数计算
不要小看transformer的这个位置编码,不少做NLP多年的人也不一定对其中的细节有多深入,而网上大部分文章谈到这个位置编码时基本都是千篇一律、泛泛而谈,很少有深入,故本文还是细致探讨下
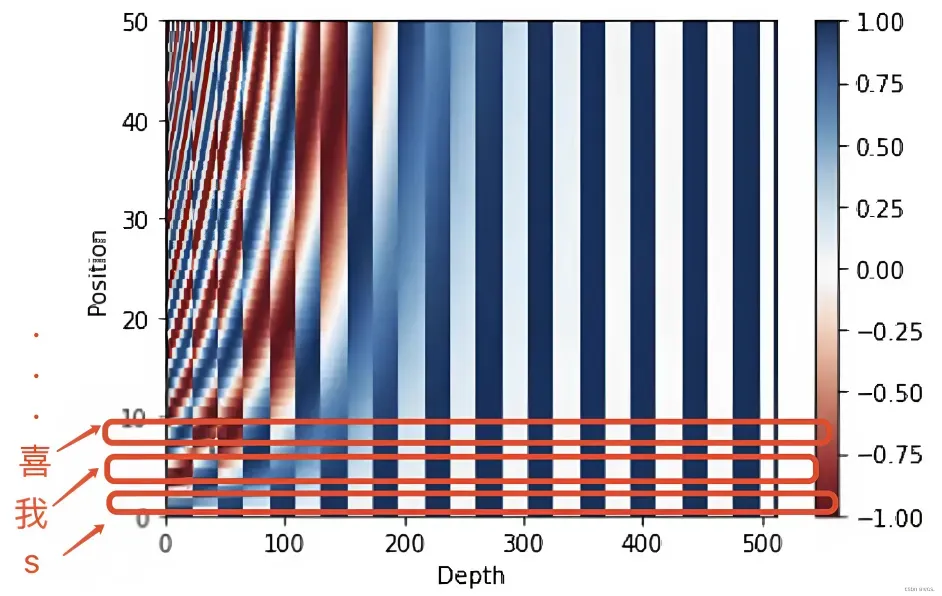
考虑到一图胜千言 一例胜万语,举个例子,当我们要编码「我 爱 你」的位置向量,假定每个token都具备512维,如果位置下标从0开始时,则根据位置编码的计算公式可得『且为让每个读者阅读本文时一目了然,我计算了每个单词对应的位置编码示例(在此之前,这些示例在其他地方基本没有)』
- 当对
上的单词「我」进行位置编码时,它本身的维度有512维
- 当对
上的单词「爱」进行位置编码时,它本身的维度有512维
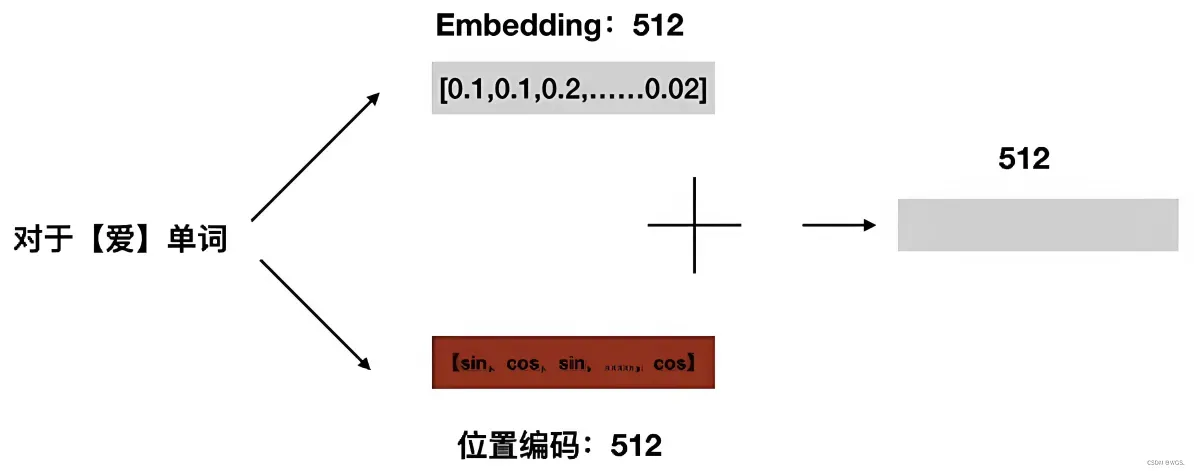
然后再叠加上embedding向量,可得
- 当对
上的单词「你」进行位置编码时,它本身的维度有512维
- ….
最终得到的可视化效果如下图所示
代码实现如下
“”“位置编码的实现,调用父类nn.Module的构造函数”“”
class PositionalEncoding(nn.Module):
def __init__(self, d_model, dropout, max_len=5000):
super(PositionalEncoding, self).__init__()
self.dropout = nn.Dropout(p=dropout) # 初始化dropout层
# 计算位置编码并将其存储在pe张量中
pe = torch.zeros(max_len, d_model) # 创建一个max_len x d_model的全零张量
position = torch.arange(0, max_len).unsqueeze(1) # 生成0到max_len-1的整数序列,并添加一个维度
# 计算div_term,用于缩放不同位置的正弦和余弦函数
div_term = torch.exp(torch.arange(0, d_model, 2) *
-(math.log(10000.0) / d_model))
# 使用正弦和余弦函数生成位置编码,对于d_model的偶数索引,使用正弦函数;对于奇数索引,使用余弦函数。
pe[:, 0::2] = torch.sin(position * div_term)
pe[:, 1::2] = torch.cos(position * div_term)
pe = pe.unsqueeze(0) # 在第一个维度添加一个维度,以便进行批处理
self.register_buffer('pe', pe) # 将位置编码张量注册为缓冲区,以便在不同设备之间传输模型时保持其状态
# 定义前向传播函数
def forward(self, x):
# 将输入x与对应的位置编码相加
x = x + Variable(self.pe[:, :x.size(1)],
requires_grad=False)
# 应用dropout层并返回结果
return self.dropout(x)本文发布之后,有同学留言问,上面中的第11行、12行代码
div_term = torch.exp(torch.arange(0, d_model, 2) * -(math.log(10000.0) / d_model))为什么先转换为了等价的指数+对数运算,而不是直接幂运算?是效率、精度方面有差异吗?
这里使用指数和对数运算的原因是为了确保数值稳定性和计算效率。
- 一方面,直接使用幂运算可能会导致数值上溢或下溢。当d_model较大时,10000.0 ** (-i / d_model)中的幂可能会变得非常小,以至于在数值计算中产生下溢。通过将其转换为指数和对数运算,可以避免这种情况,因为这样可以在计算过程中保持更好的数值范围
- 二方面,在许多计算设备和库中,指数和对数运算的实现通常比幂运算更快。这主要是因为指数和对数运算在底层硬件和软件中有特定的优化实现,而幂运算通常需要计算更多的中间值
所以,使用指数和对数运算可以在保持数值稳定性的同时提高计算效率。
既然提到了这行代码,我们干脆就再讲更细致些,上面那行代码对应的公式为
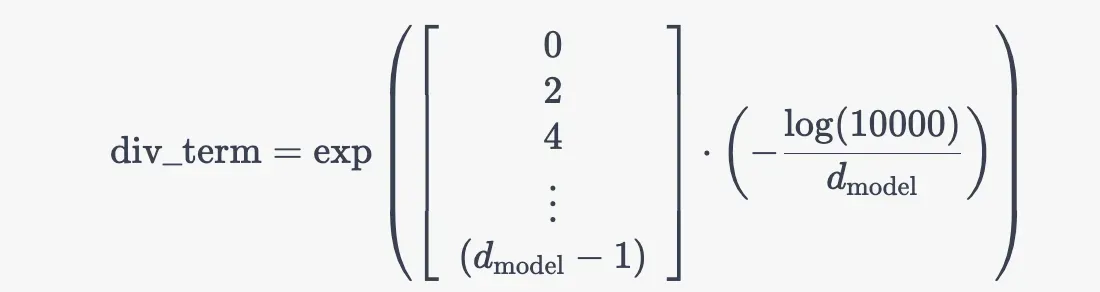
其中的中括号对应的是一个从 0 到 的等差数列(步长为 2),设为
且上述公式与这个公式是等价的
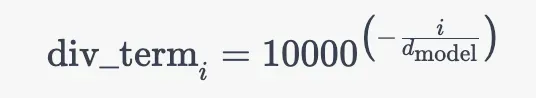
为何,原因在于,从而有
最终,再通过下面这两行代码完美实现位置编码
# 使用正弦和余弦函数生成位置编码,对于d_model的偶数索引,使用正弦函数;对于奇数索引,使用余弦函数。
pe[:, 0::2] = torch.sin(position * div_term)
pe[:, 1::2] = torch.cos(position * div_term)1.2 经过「embedding + 位置编码」后乘以三个权重矩阵得到三个向量Q K V
从下图可知,经过「embedding + 位置编码」得到的输入,会乘以「三个权重矩阵:
」得到查询向量Q、键向量K、值向量V(你可以简单粗暴的理解为弄出来了三个分身)
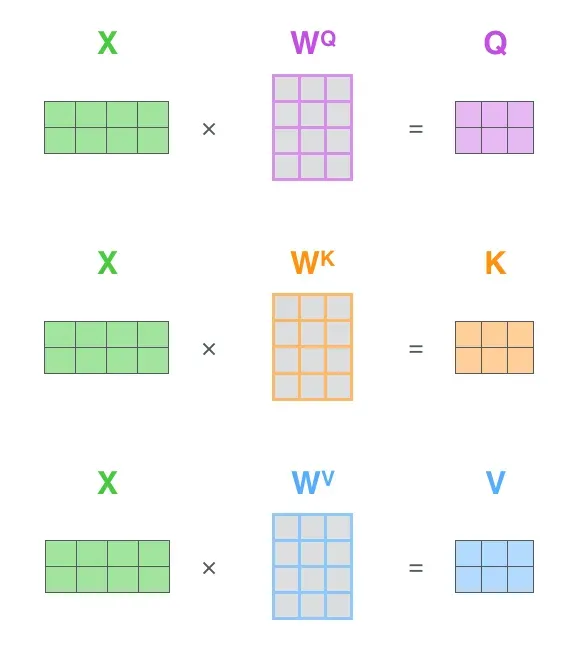
举个例子,针对「我想吃酸菜鱼」这句话,经过embedding + 位置编码后,可得(注:可以512维,也可以是768维,但由于transformer论文中作者设置的512维,所以除了这个酸菜鱼的例子暂为768维外,其他地方均统一为512维)

然后乘以三个权重矩阵得
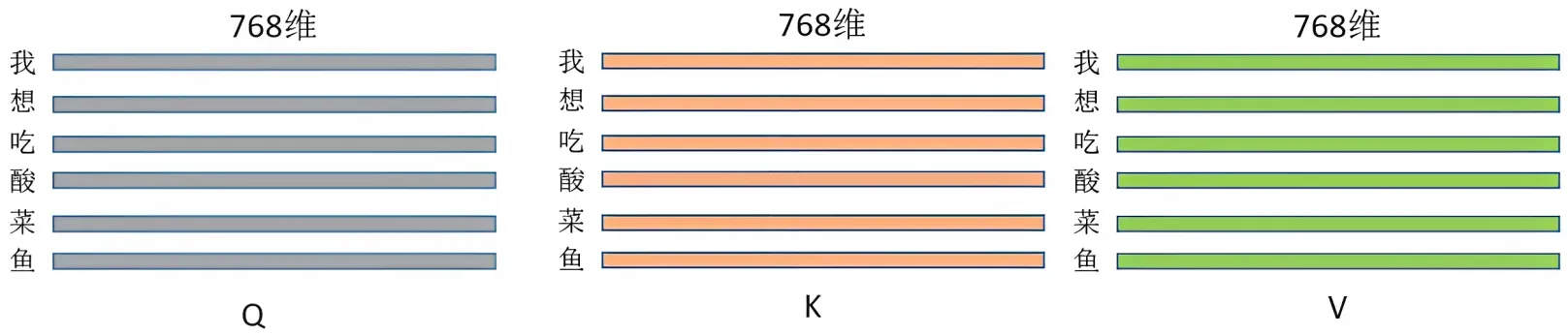
为此,我们可以先创建4个相同的线性层,每个线性层都具有 d_model 的输入维度和 d_model 的输出维度
self.linears = clones(nn.Linear(d_model, d_model), 4) 前三个线性层分别用于对 Q向量、K向量、V向量进行线性变换(至于这第4个线性层在随后的第3点)
1.3 对输入和Multi-Head Attention做Add&Norm,再对上步输出和Feed Forward做Add&Norm
我们聚焦下transformer论文中原图的这部分,可知,输入通过embedding+位置编码后,先后做以下两个步骤
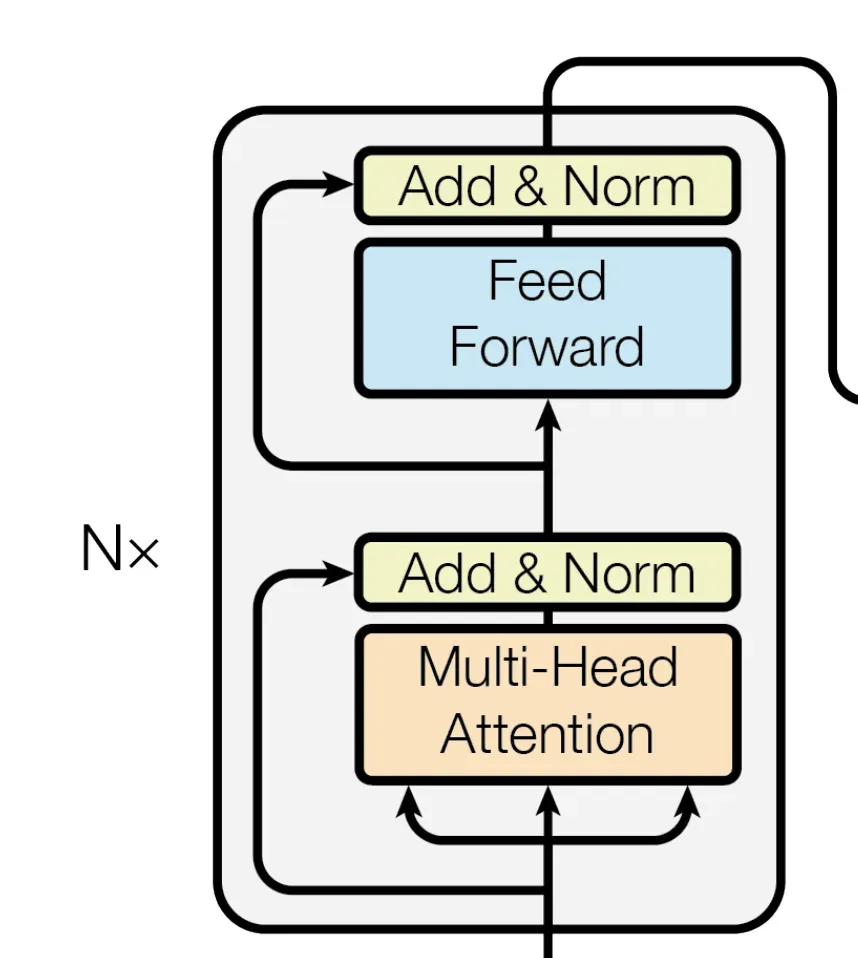
- 针对query向量做multi-head attention,得到的结果与原query向量,做相加并归一化
这个相加具体是怎么个相加法呢?事实上,Add代表的Residual Connection(残差连接),是为了解决多层神经网络训练困难的问题,通过将前一层的信息无差的传递到下一层,可以有效的仅关注差异部分,这一方法之前在图像处理结构如ResNet等中常常用到attention = self.attention(query, key, value, mask) output = self.dropout(self.norm1(attention + query))
具体编码时通过 SublayerConnection 函数实现此功能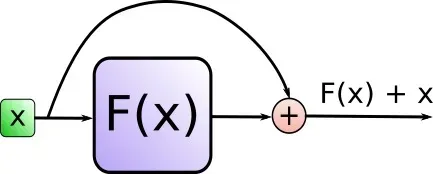
而Norm则代表了Layer Normalization,通过对层的激活值的归一化,可以加速模型的训练过程,使其更快的收敛,编码时用 LayerNorm 函数实现"""一个残差连接(residual connection),后面跟着一个层归一化(layer normalization)操作""" class SublayerConnection(nn.Module): # 初始化函数,接收size(层的维度大小)和dropout(dropout率)作为输入参数 def __init__(self, size, dropout): super(SublayerConnection, self).__init__() # 调用父类nn.Module的构造函数 self.norm = LayerNorm(size) # 定义一个层归一化(Layer Normalization)操作,使用size作为输入维度 self.dropout = nn.Dropout(dropout) # 定义一个dropout层 # 定义前向传播函数,输入参数x是输入张量,sublayer是待执行的子层操作 def forward(self, x, sublayer): # 将残差连接应用于任何具有相同大小的子层 # 首先对输入x进行层归一化,然后执行子层操作(如self-attention或前馈神经网络) # 接着应用dropout,最后将结果与原始输入x相加。 return x + self.dropout(sublayer(self.norm(x)))"""构建一个层归一化(layernorm)模块""" class LayerNorm(nn.Module): # 初始化函数,接收features(特征维度大小)和eps(防止除以零的微小值)作为输入参数 def __init__(self, features, eps=1e-6): super(LayerNorm, self).__init__() # 调用父类nn.Module的构造函数 self.a_2 = nn.Parameter(torch.ones(features)) # 定义一个大小为features的一维张量,初始化为全1,并将其设置为可训练参数 self.b_2 = nn.Parameter(torch.zeros(features)) # 定义一个大小为features的一维张量,初始化为全0,并将其设置为可训练参数 self.eps = eps # 将防止除以零的微小值eps保存为类实例的属性 # 定义前向传播函数,输入参数x是输入张量 def forward(self, x): mean = x.mean(-1, keepdim=True) # 计算输入x在最后一个维度上的均值,保持输出结果的维度 std = x.std(-1, keepdim=True) # 计算输入x在最后一个维度上的标准差,保持输出结果的维度 # 对输入x进行层归一化,使用可训练参数a_2和b_2进行缩放和偏移,最后返回归一化后的结果 return self.a_2 * (x - mean) / (std + self.eps) + self.b_2 - 上面步骤得到的『输出结果output做feed forward』之后,再与『上面步骤的原输出结果output』也做相加并归一化
forward = self.feed_forward(output) block_output = self.dropout(self.norm2(forward + output)) return block_output
总而言之,上述过程用公式表达则如下
第一步中的X代表Multi-Head Attention,第二步中的X代表FFN(本质上就是一个全连接层MLP),最终这个编码器层代码可以完整的写为
"""编码器(Encoder)由自注意力(self-attention)层和前馈神经网络(feed forward)层组成"""
class EncoderLayer(nn.Module):
# 初始化函数,接收size(层的维度大小)、self_attn(自注意力层实例)
# feed_forward(前馈神经网络实例)和dropout(dropout率)作为输入参数
def __init__(self, size, self_attn, feed_forward, dropout):
super(EncoderLayer, self).__init__() # 调用父类nn.Module的构造函数
self.self_attn = self_attn # 将自注意力层实例保存为类实例的属性
self.feed_forward = feed_forward # 将前馈神经网络实例保存为类实例的属性
# 创建两个具有相同参数的SublayerConnection实例(用于残差连接和层归一化)
self.sublayer = clones(SublayerConnection(size, dropout), 2)
self.size = size # 将层的维度大小保存为类实例的属性
def forward(self, x, mask):
# 先对输入x进行自注意力操作
# 然后将结果传递给第一个SublayerConnection实例(包括残差连接和层归一化)
x = self.sublayer[0](x, lambda x: self.self_attn(x, x, x, mask))
# 将上一步的输出传递给前馈神经网络
# 然后将结果传递给第二个SublayerConnection实例(包括残差连接和层归一化),最后返回结果
return self.sublayer[1](x, self.feed_forward)1.3.1 缩放点积注意力(Scaled Dot-Product Attention)
接下来,先看下缩放点积注意力(Scaled Dot-Product Attention)的整体实现步骤
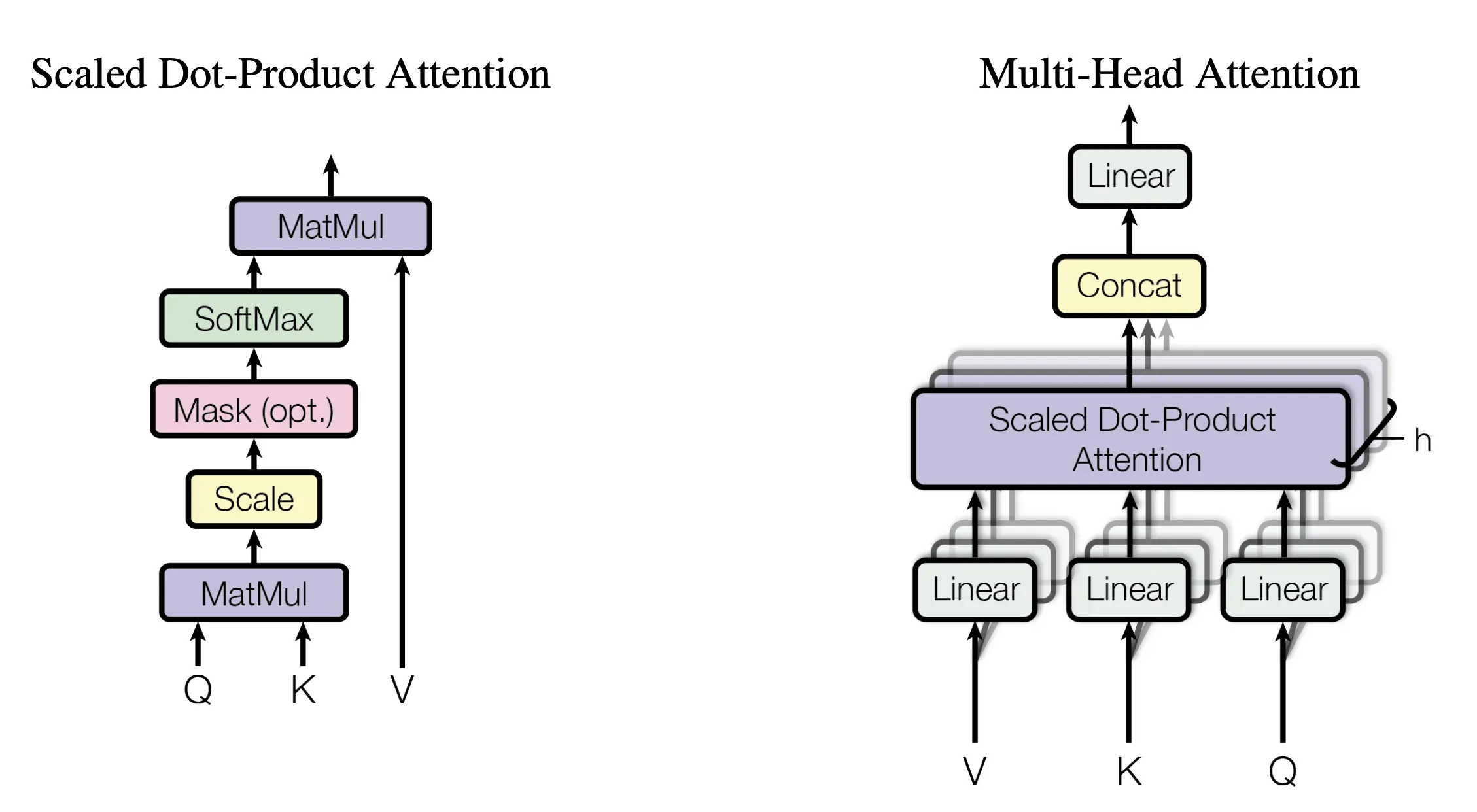
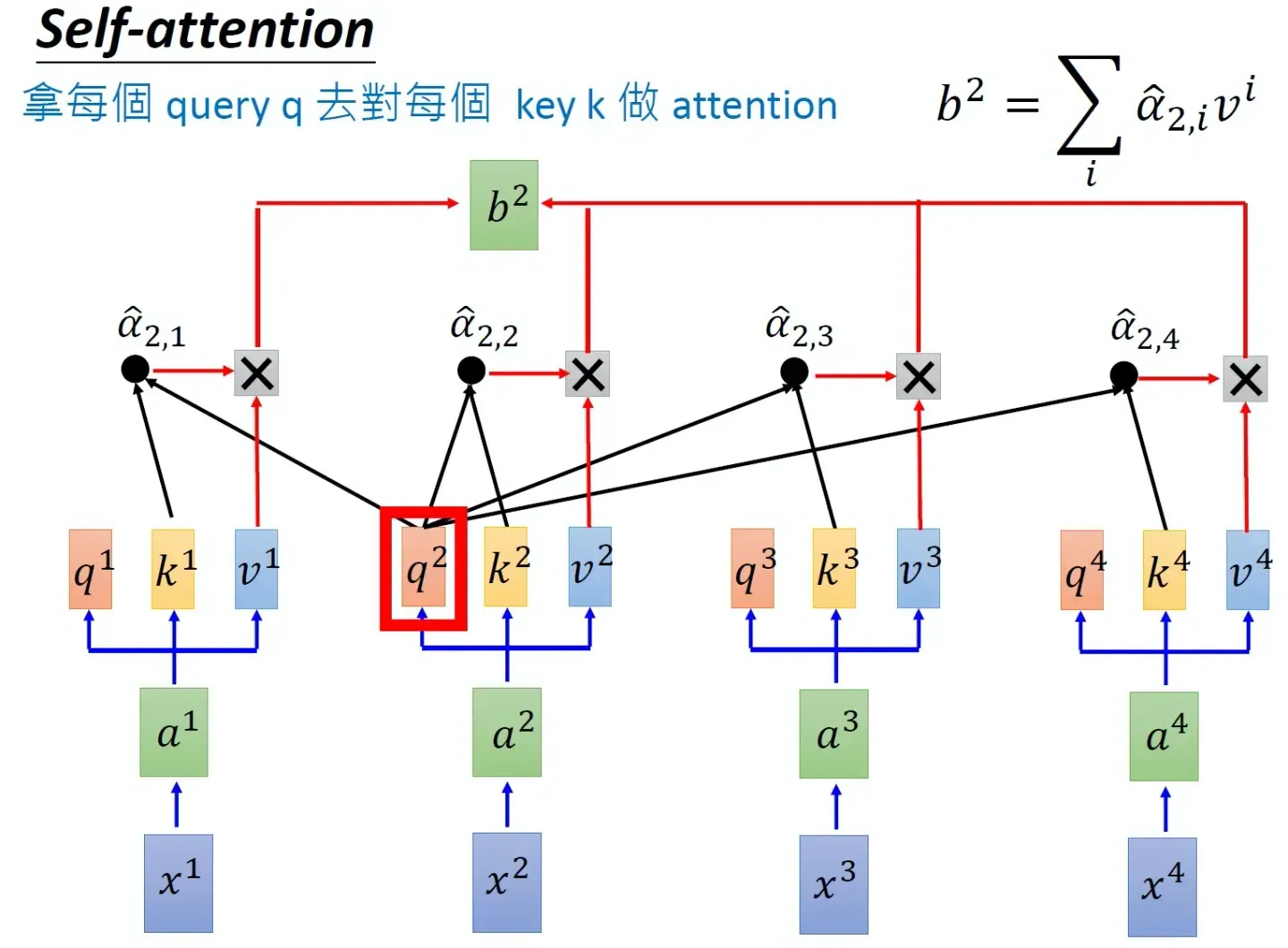
- 为了计算每个单词与其他单词之间的相似度,会拿「每个单词/token的q向量」与「包括自身在内所有单词/token的k向量」一一做点积(两个向量之间的点积结果可以代表两个向量的相似度)
对应到矩阵的形式上,则是矩阵Q与K矩阵的转置做相乘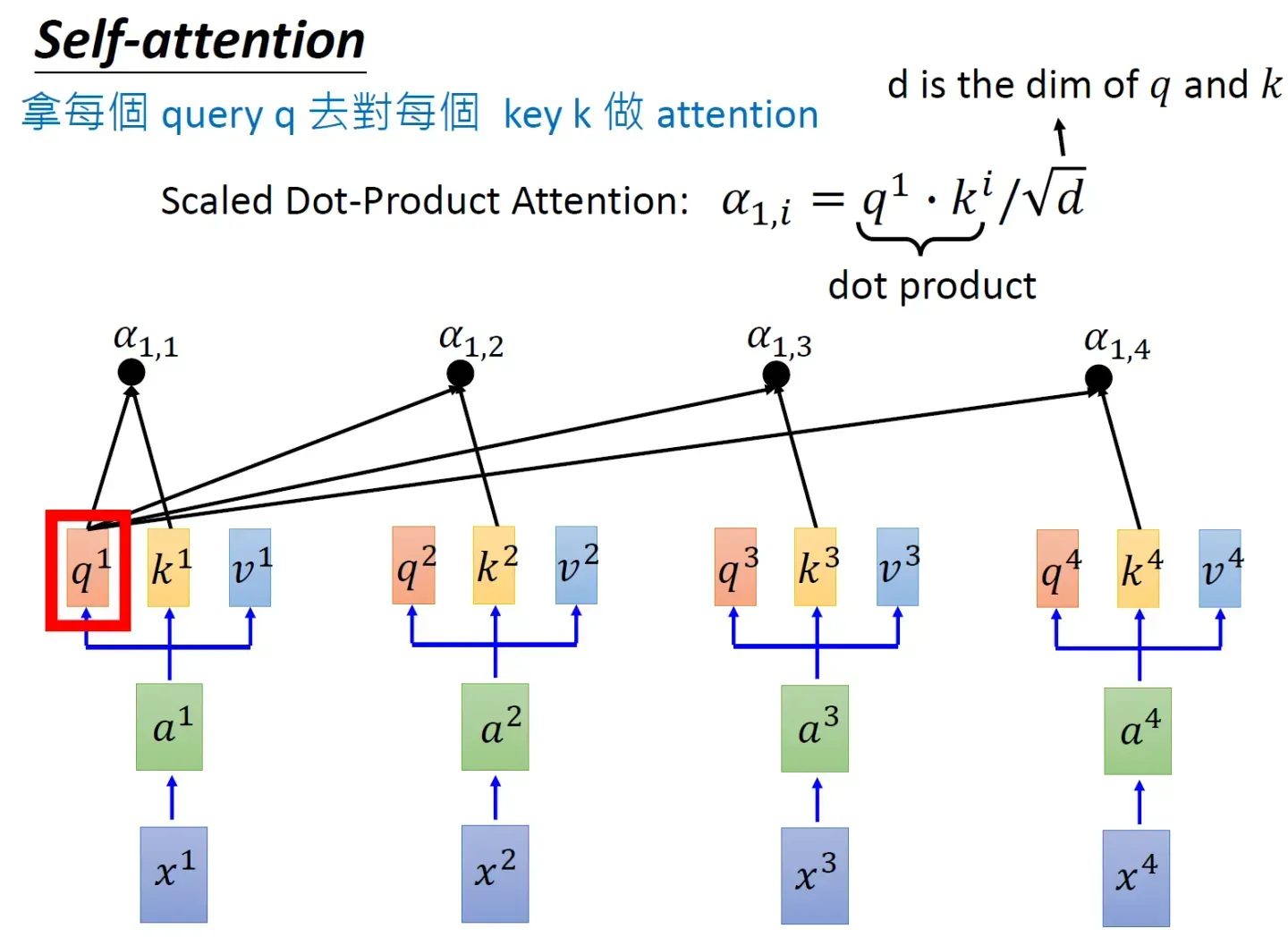
还是拿上面那个例子:「我想吃酸菜鱼」,则Q乘以K的转置如下图所示
最终得到的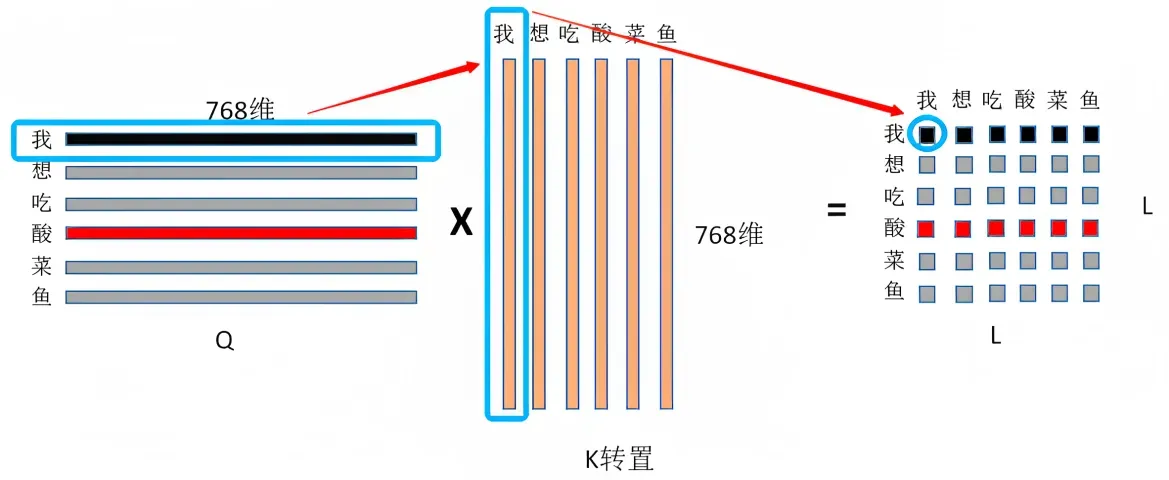
矩阵有6行6列,从上往下逐行来看的话,每一个格子里都会有一个数值,每一个数值依次代表:
单词我与「我 想 吃 酸 菜 鱼」各自的点积结果或相似度,比如可能是0.3 0.2 0.2 0.1 0.1 0.1,代表编码1时放在「我 想 吃 酸 菜 鱼」上面的注意力大小
同时,可以看到模型在对当前位置的信息进行编码时,会过度的将注意力集中于自身的位置(当然 这无可厚非,毕竟自己与自己最相似嘛),而可能忽略了其它位置。很快你会看到,作者采取的一种解决方案就是采用多头注意力机制(Multi-Head Attention)想与「我 想 吃 酸 菜 鱼」各自的点积结果或相似度
吃与「我 想 吃 酸 菜 鱼」各自的点积结果或相似度
酸与「我 想 吃 酸 菜 鱼」各自的点积结果或相似度
菜与「我 想 吃 酸 菜 鱼」各自的点积结果或相似度
鱼与「我 想 吃 酸 菜 鱼」各自的点积结果或相似度
- 由于
会随着dimension的增大而增大,为避免过大,所以除以
,相当于对点积的结果做下缩放
其中,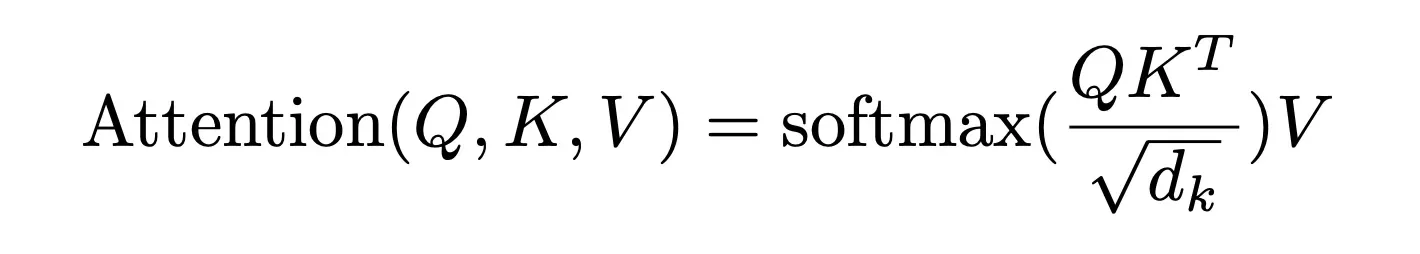
是向量
的维度,且
,如果只设置了一个头,那
就是模型的维度
,如果设置了8个头,则
,且如果模型的维度是512维,则
即等于8
上面两步的代码可以如下编写# torch.matmul是PyTorch库提供的矩阵乘法函数 # 具体操作即是将第一个矩阵的每一行与第二个矩阵的每一列进行点积(对应元素相乘并求和),得到新矩阵的每个元素 scores = torch.matmul(query, key.transpose(-2, -1)) \ / math.sqrt(d_k) - 接着使用 Softmax 计算每一个单词对包括自身在内所有单词的 Attention值,这些值加起来的和为1(相当于起到了归一化的效果)
这步对应的代码为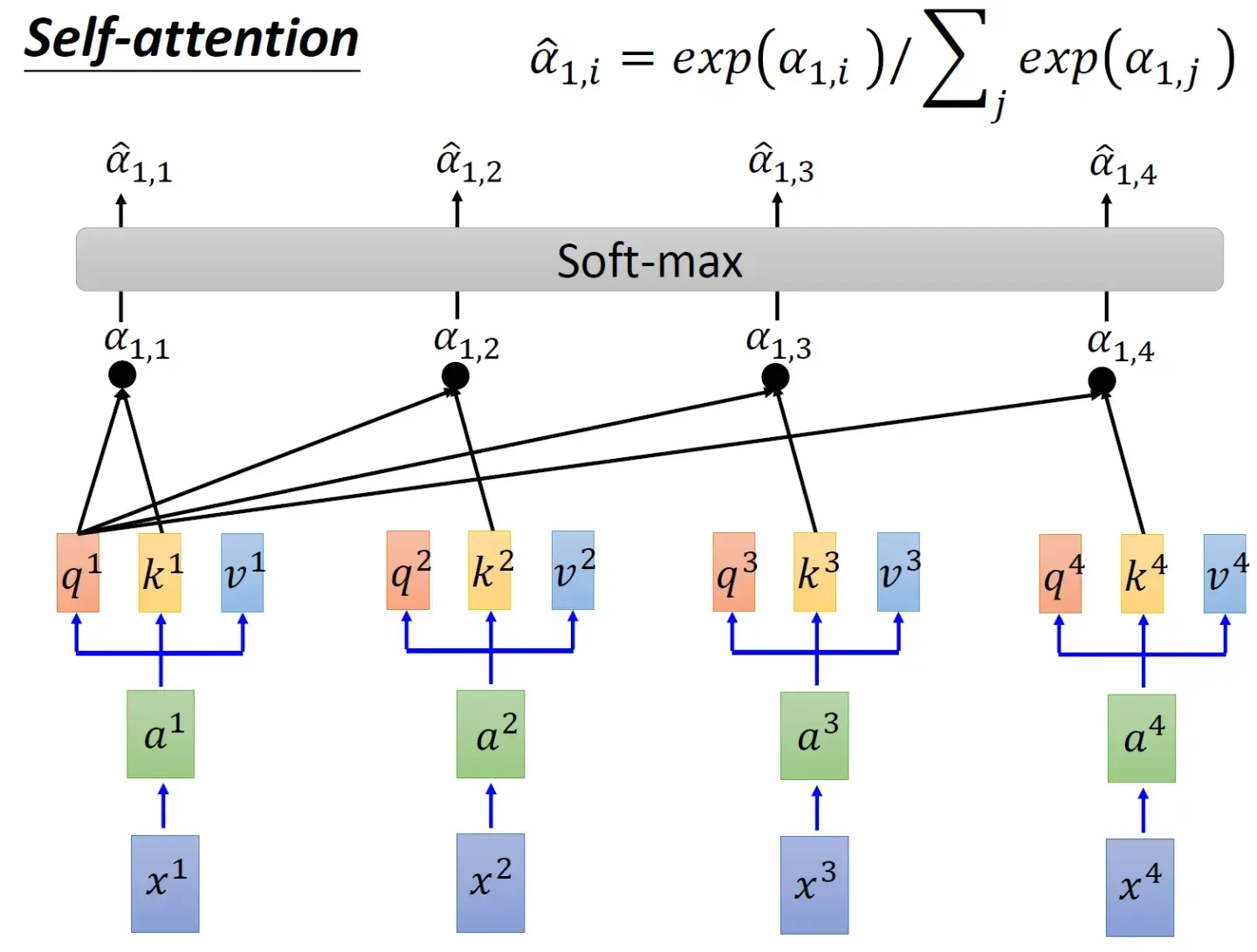
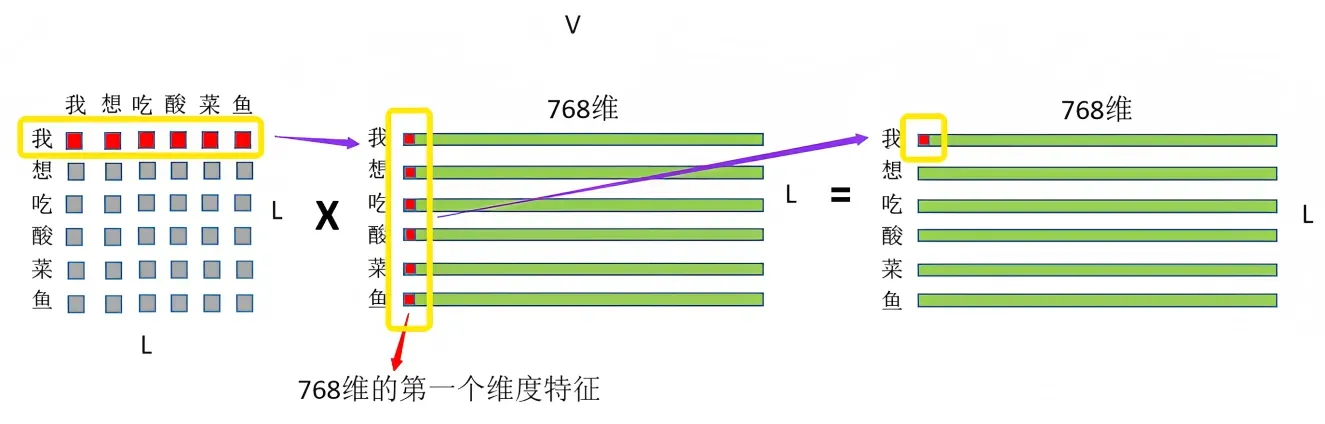
# 对 scores 进行 softmax 操作,得到注意力权重 p_attn p_attn = F.softmax(scores, dim = -1) - 最后再乘以
矩阵,即对所有values(v1 v2 v3 v4),根据不同的attention值(
),做加权平均
对应到我想吃酸菜鱼这个例子上,则是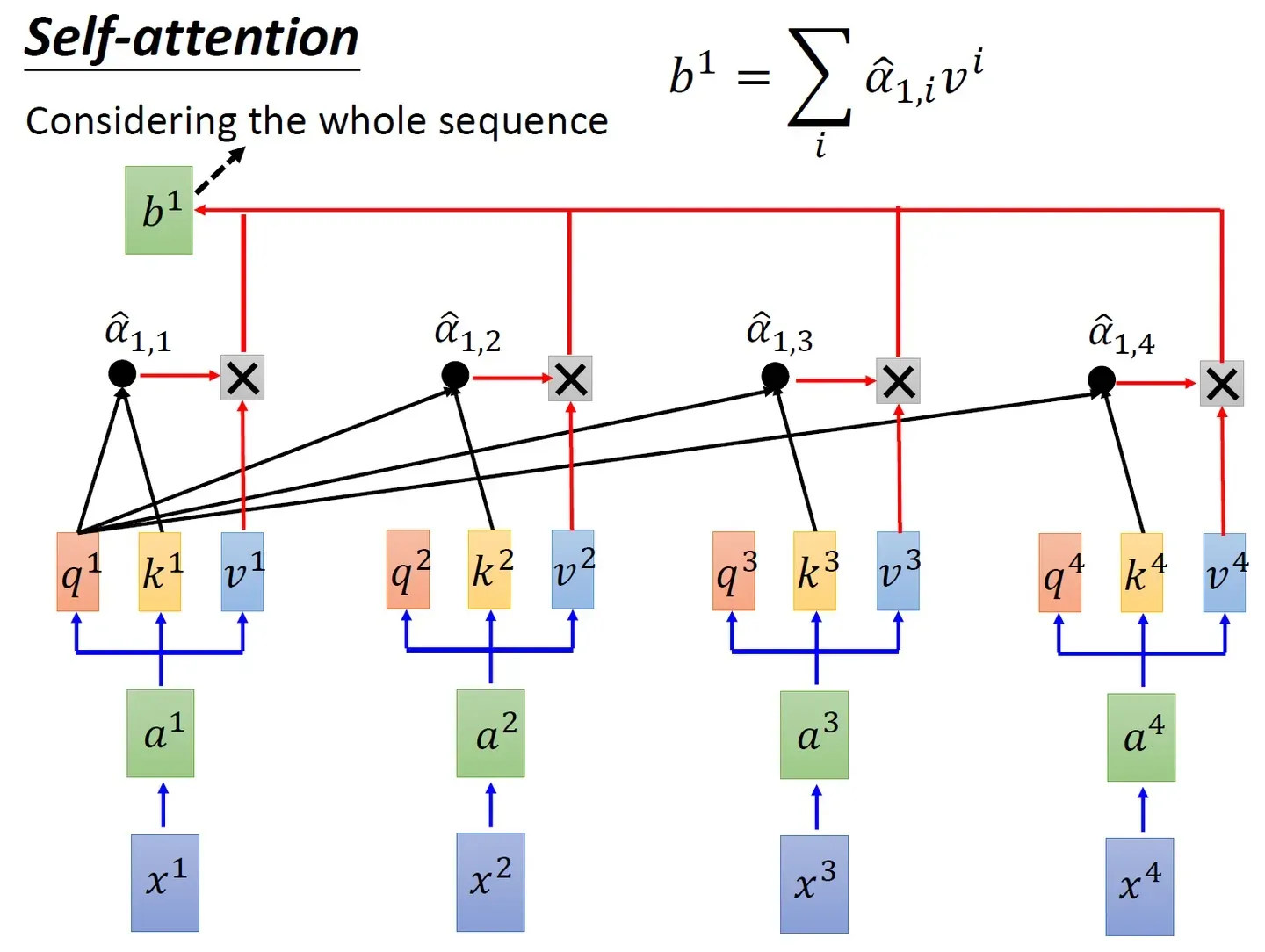
- 最终得到单词的输出,如下图所示(图中V矩阵的4行分别代表v1 v2 v3 v4):
上述两步对应的代码为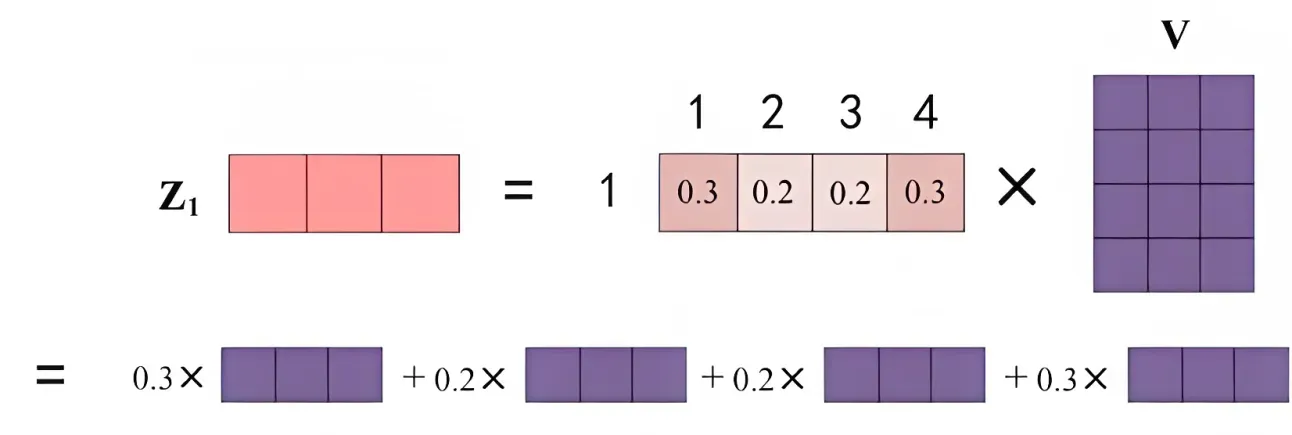
# 用注意力权重 p_attn 对 value 向量进行加权求和,得到最终的输出 return torch.matmul(p_attn, value), p_attn
同样的方法,也可以计算出,如下图8所示, b2就是拿q2去对其他的key做attention,最后再与其他的value值相乘取weighted sum得到,最终每个单词都包含了上下文相关单词的语义信息,不再只是attention计算之前,每个单词只有它自己的信息,和上下文没有关联
另外,这里面还有一点值得注意的是,可能有同学疑问:当我们计算x1与x2、x3、x4的相似度之后,x2会再与x1、x3、x4再依次计算一遍相似度,这两个过程中,前者算过了x1和x2的相似度,后者则再算一遍x2与x1的相似度,这不是重复计算么?其实不然,这是两码事,原因很简单,正如你喜欢一个人 你会觉得她对你很重要,但那个人不一定喜欢你 她不会觉得你对她有多重要..
最终,Scaled Dot-Product Attention这部分对应的完整代码可以写为
'''计算“缩放点积注意力'''
# query, key, value 是输入的向量组
# mask 用于遮掩某些位置,防止计算注意力
# dropout 用于添加随机性,有助于防止过拟合
def attention(query, key, value, mask=None, dropout=None):
d_k = query.size(-1) # 获取 query 向量的最后一个维度的大小,即词嵌入的维度
# 计算 query 和 key 的点积,并对结果进行缩放,以减少梯度消失或爆炸的可能性
scores = torch.matmul(query, key.transpose(-2, -1)) \
/ math.sqrt(d_k)
# 如果提供了 mask,根据 mask 对 scores 进行遮掩
# 遮掩的具体方法就是设为一个很大的负数比如-1e9,从而softmax后 对应概率基本为0
if mask is not None:
scores = scores.masked_fill(mask == 0, -1e9)
# 对 scores 进行 softmax 操作,得到注意力权重 p_attn
p_attn = F.softmax(scores, dim = -1)
# 如果提供了 dropout,对注意力权重 p_attn 进行 dropout 操作
if dropout is not None:
p_attn = dropout(p_attn)
# 用注意力权重 p_attn 对 value 向量进行加权求和,得到最终的输出
return torch.matmul(p_attn, value), p_attn1.3.2 多头注意力(Multi-Head Attention)
先看2个头的例子,依然还是通过生成对应的三个矩阵
、
、
,然后这三个矩阵再各自乘以两个转移矩阵得到对应的分矩阵,如
矩阵对应的两个分矩阵
、
矩阵对应的两个分矩阵为
、
矩阵对应的两个分矩阵为
、
至于同理,也生成对应的6个分矩阵
、
、
、
、
、
接下来编码时,分两步
先与
做点积然后乘以
,然后再与
做点积再乘以
,再把这两个计算的结果相加得到
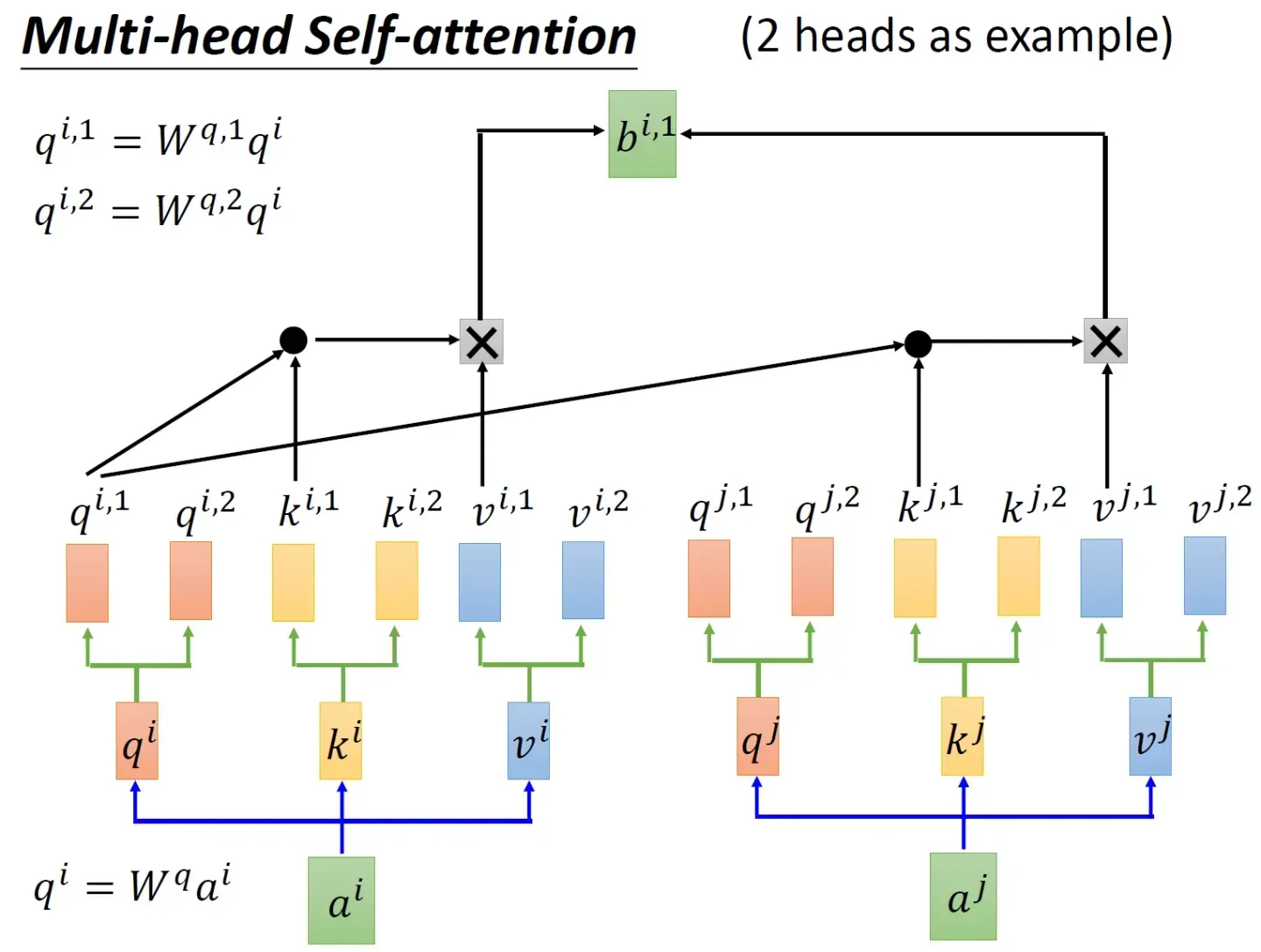
再分别与
做点积然后乘以
、然后再与
做点积再乘以
,再把这两个计算的结果相加得到
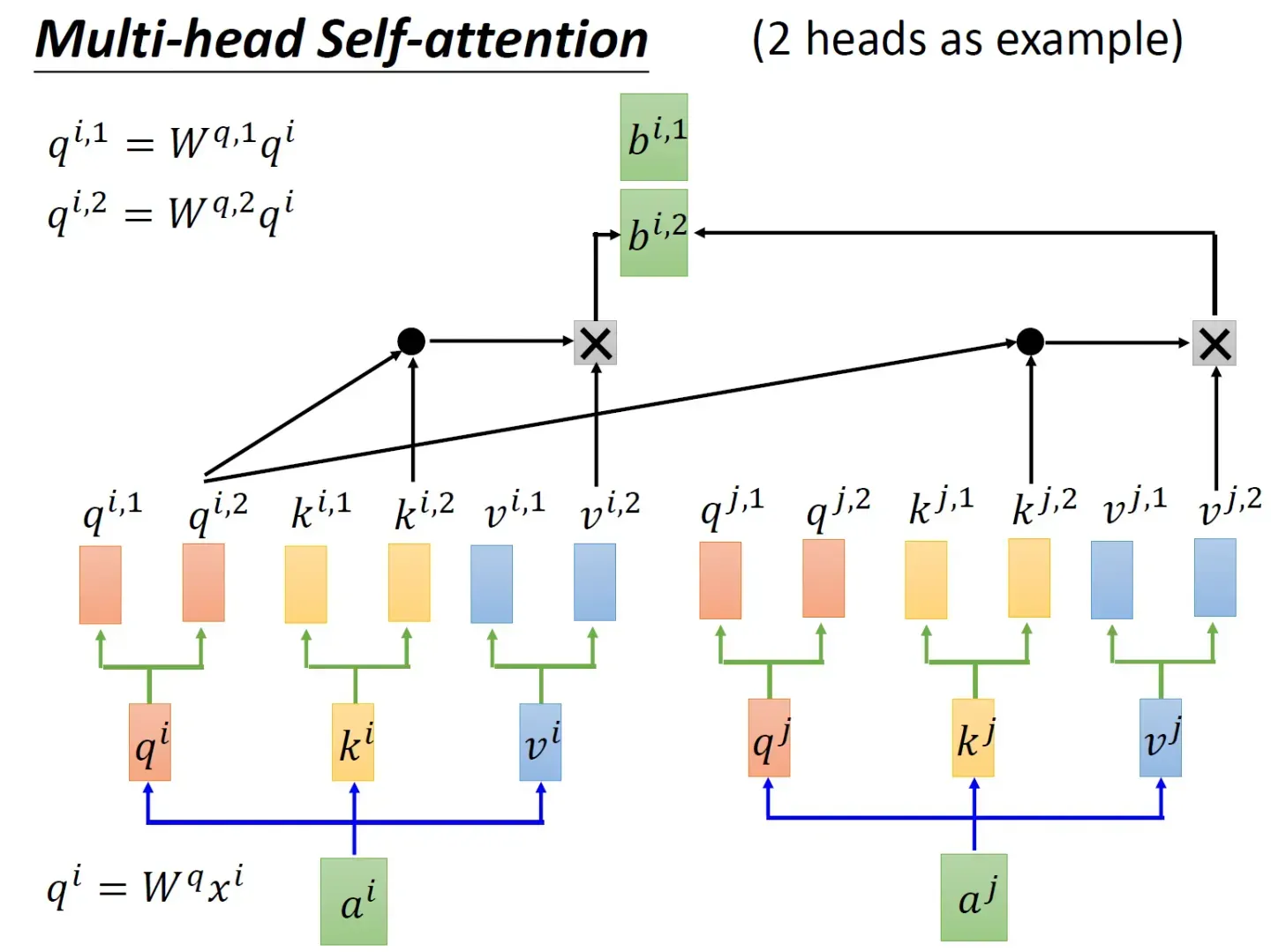
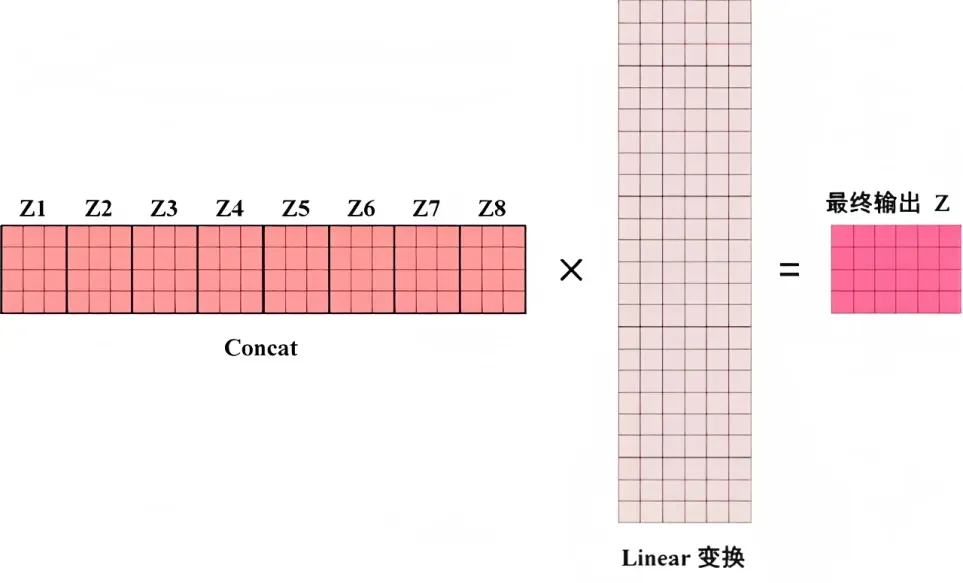
如果是8个头呢,计算步骤上也是一样的,只是从2个头变化到8个头而已,最终把每个头得到的结果直接concat,最后经过一个linear变换,得到最终的输出,整体如下所示
这部分Multi-Head Attention的代码可以写为
'''代码来自nlp.seas.harvard.edu,我针对每一行代码、甚至每行代码中的部分变量都做了详细的注释/解读'''
class MultiHeadedAttention(nn.Module):
# 输入模型的大小(d_model)和注意力头的数量(h)
def __init__(self, h, d_model, dropout=0.1):
super(MultiHeadedAttention, self).__init__()
assert d_model % h == 0 # 确保 d_model 可以被 h 整除
# 我们假设 d_v(值向量的维度)总是等于 d_k(键向量的维度)
self.d_k = d_model // h # 计算每个注意力头的维度
self.h = h # 保存注意力头的数量
self.linears = clones(nn.Linear(d_model, d_model), 4) # 上文解释过的四个线性层
self.attn = None # 初始化注意力权重为 None
self.dropout = nn.Dropout(p=dropout) # 定义 dropout 层
# 实现多头注意力的前向传播
def forward(self, query, key, value, mask=None):
if mask is not None:
# 对所有 h 个头应用相同的 mask
mask = mask.unsqueeze(1)
nbatches = query.size(0) # 获取 batch 的大小
# 1) 批量执行从 d_model 到 h x d_k 的线性投影
query, key, value = \
[l(x).view(nbatches, -1, self.h, self.d_k).transpose(1, 2)
for l, x in zip(self.linears, (query, key, value))]
# 2) 在批量投影的向量上应用注意力
# 具体方法是调用上面实现Scaled Dot-Product Attention的attention函数
x, self.attn = attention(query, key, value, mask=mask,
dropout=self.dropout)
# 3) 使用 view 函数进行“拼接concat”,然后做下Linear变换
x = x.transpose(1, 2).contiguous() \
.view(nbatches, -1, self.h * self.d_k)
return self.linears[-1](x) # 返回多头注意力的输出1.3.3 Position-wise前馈网络的实现
在上文,咱们逐一编码实现了embedding、位置编码、缩放点积/多头注意力,以及Add和Norm,整个编码器部分还剩最后一个模块,即下图框里的Feed Forward Network(简称FFN)
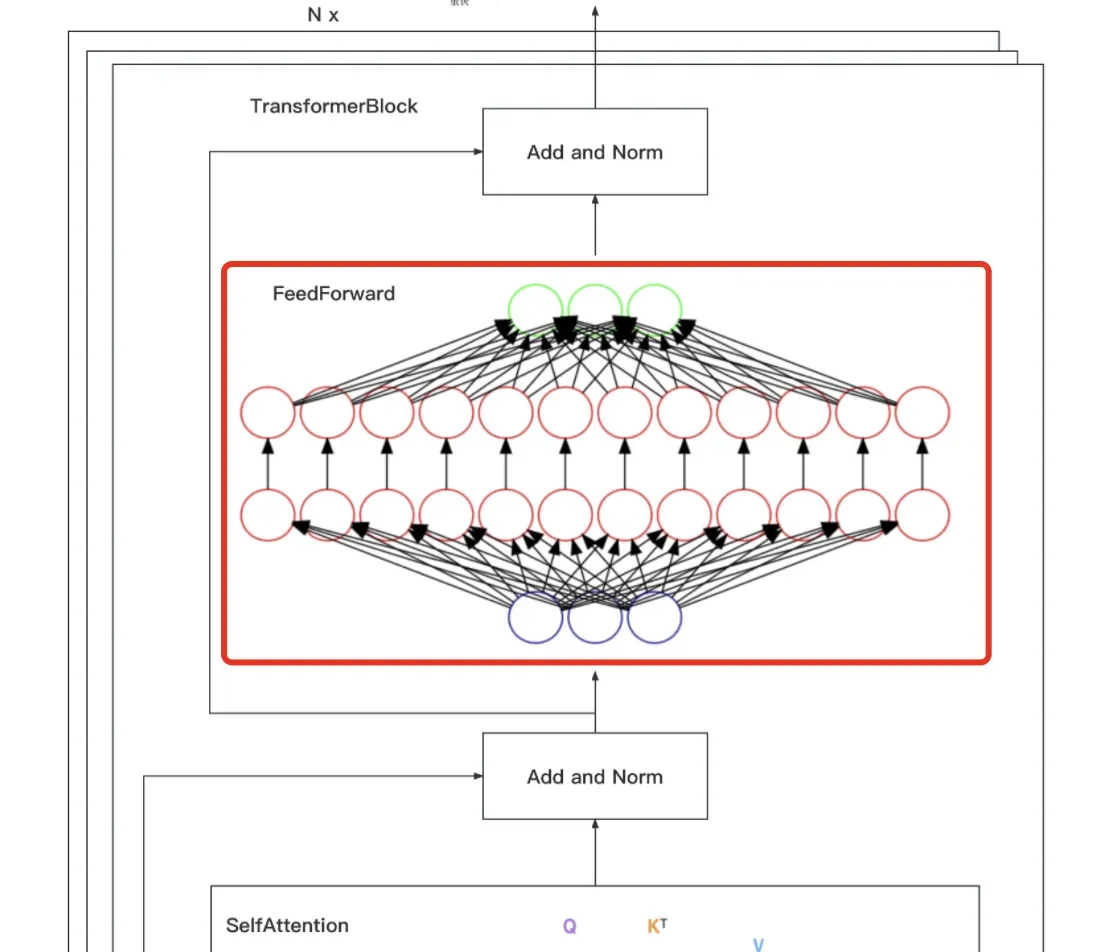
其中包括两个线性变换:维度上先扩大后缩小,最终输入和输出的维数为,内层的维度为
,过程中使用ReLU作为激活函数
虽然线性变换在不同位置上是相同的,但它们在层与层之间使用不同的参数,相当于使用了两个内核大小为1的卷积
这部分的代码可以如下编写
‘’‘定义一个名为PositionwiseFeedForward的类,继承自nn.Module’‘’
class PositionwiseFeedForward(nn.Module):
# 文档字符串:实现FFN方程
# 初始化方法,接受三个参数:d_model,d_ff和dropout(默认值为0.1)
def __init__(self, d_model, d_ff, dropout=0.1):
# 调用父类nn.Module的初始化方法
super(PositionwiseFeedForward, self).__init__()
self.w_1 = nn.Linear(d_model, d_ff) # 定义一个全连接层,输入维度为d_model,输出维度为d_ff
self.w_2 = nn.Linear(d_ff, d_model) # 定义一个全连接层,输入维度为d_ff,输出维度为d_model
self.dropout = nn.Dropout(dropout) # 定义一个dropout层,dropout概率为传入的dropout参数
# 定义前向传播方法,接受一个输入参数x
def forward(self, x):
# 将输入x通过第一个全连接层w_1后,经过ReLU激活函数,再通过dropout层,最后通过第二个全连接层w_2,返回最终结果
return self.w_2(self.dropout(F.relu(self.w_1(x))))1.4 对整个transformer block复制N份最终成整个encode模块
N可以等于6或其他数值
class Encoder(nn.Module): # 定义一个名为Encoder的类,它继承了nn.Module类
# 一个具有N层堆叠的核心编码器
# 初始化方法,接受两个参数:layer(编码器层的类型)和N(编码器层的数量)
def __init__(self, layer, N):
super(Encoder, self).__init__() # 调用父类nn.Module的初始化方法
self.layers = clones(layer, N) # 创建N个编码器层的副本,并将其赋值给实例变量self.layers
self.norm = LayerNorm(layer.size) # 创建一个LayerNorm层,并将其赋值给实例变量self.norm
# 定义前向传播方法,接受两个参数:x(输入数据)和mask(掩码)
def forward(self, x, mask):
# 文档字符串:解释本方法的功能是将输入(及其掩码)依次传递给每一层
for layer in self.layers: # 遍历self.layers中的每一个编码器层
x = layer(x, mask) # 将输入x和mask传递给当前编码器层,并将输出结果赋值给x
return self.norm(x) # 对最终的输出x应用LayerNorm层,并将结果返回其中的clone函数的代码为
def clones(module, N):
"Produce N identical layers."
return nn.ModuleList([copy.deepcopy(module) for _ in range(N)])第二部分 从零实现Transformer解码器模块
咱们再回顾下transformer的整个模型架构,特别是解码器的部分,毕竟BERT外,GPT等很有影响力的模型都用的transformer decode结构

从底至上,
- 输入包括2部分,下方是前一个time step的输出的embedding
再加上一个表示位置的Positional Encoding - 接着是Masked Multi-Head Self-attention,masked字面意思是屏蔽
然后做一下Add&Norm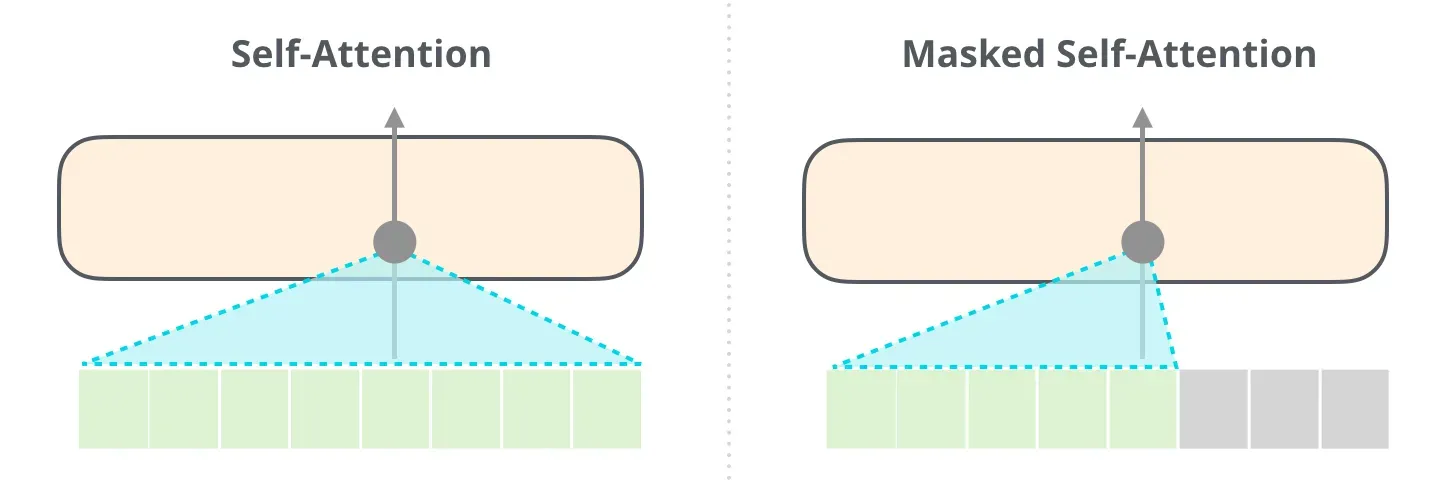
- 再往上是一个不带mask的Multi-Head Attention层,它的Key、Value矩阵使用 Encoder 的编码信息矩阵,而Query使用上一个 Decoder block 的输出计算
然后再做一下Add&Norm - 继续往上,经过一个FFN层,也做一下Add&Norm
- 最后做下linear变换后,通过Softmax 层计算下一个翻译单词的概率
由于在第一部分介绍过了embedding、positional encoding、FFN、Add&Norm、linear、softmax、multi-head attention,故本部分只重点介绍下Masked Multi-Head Self-attention
2.1 Masked Multi-Head Self-attention
本过程和第一部分介绍的Multi-Head self-attention基本一致,区别在于加了个mask机制
- 输入经过embedding + 位置编码之后,还是乘以三个不同的权重矩阵:
、
、
,依次得到三个不同的矩阵输入:Q、K、V
- Q矩阵乘以K矩阵的转置
,得到
,注意,紧接着
会再乘以一个Mask矩阵,得到Masked Attention矩阵
- Masked Attention矩阵经过softmax后,乘以V矩阵得到
矩阵
- 最终把
、
拼接之后,再做一个linear变换得到最终的
矩阵
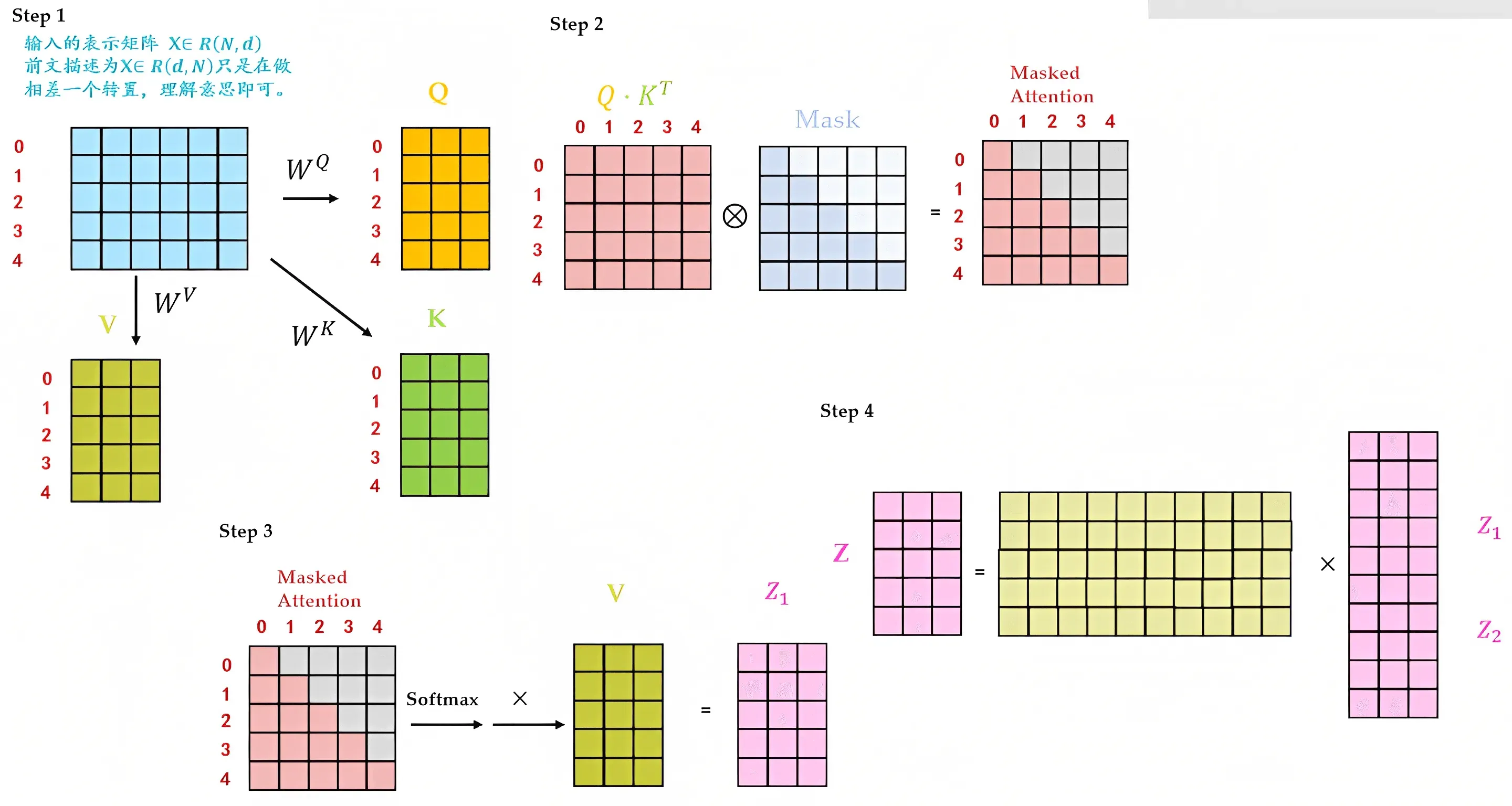
2.2 transformer解码器架构与整体编码-解码架构的实现
整个解码器架构的代码可以如下编写『有一点值得注意的是,如下文代码中所述
- 在对输入x执行自注意力计算并进行第一个子层的处理(带mask),最后一个参数是tgt_mask,即x = self.sublayer[0](x, lambda x: self.self_attn(x, x, x, tgt_mask))
- 但对输入x执行源注意力计算并进行第二个子层的处理时(不带mask),最后一个参数是src_mask,即x = self.sublayer[1](x, lambda x: self.src_attn(x, m, m, src_mask)) 』
# 定义DecoderLayer类,继承自PyTorch的nn.Module类
class DecoderLayer(nn.Module):
# 初始化方法,接收五个参数:size, self_attn, src_attn, feed_forward, dropout
# 调用父类nn.Module的初始化方法
def __init__(self, size, self_attn, src_attn, feed_forward, dropout):
super(DecoderLayer, self).__init__()
# 将size赋值给实例变量self.size
self.size = size
# 将self_attn赋值给实例变量self.self_attn
self.self_attn = self_attn
# 将src_attn赋值给实例变量self.src_attn
self.src_attn = src_attn
# 将feed_forward赋值给实例变量self.feed_forward
self.feed_forward = feed_forward
# 使用SublayerConnection类创建三个子层,并存储到实例变量self.sublayer中
self.sublayer = clones(SublayerConnection(size, dropout), 3)
# 定义前向传播方法,接收四个参数:x, memory, src_mask, tgt_mask
def forward(self, x, memory, src_mask, tgt_mask):
# 将memory赋值给局部变量m
m = memory
# 对输入x执行自注意力计算并进行第一个子层的处理
x = self.sublayer[0](x, lambda x: self.self_attn(x, x, x, tgt_mask))
# 对输入x执行源注意力计算并进行第二个子层的处理
x = self.sublayer[1](x, lambda x: self.src_attn(x, m, m, src_mask))
# 对输入x执行前馈神经网络计算并进行第三个子层的处理,然后返回结果
return self.sublayer[2](x, self.feed_forward)且Decoder也是由N=6个相同层组成
class Decoder(nn.Module):
"Generic N layer decoder with masking."
def __init__(self, layer, N):
super(Decoder, self).__init__()
self.layers = clones(layer, N)
self.norm = LayerNorm(layer.size)
def forward(self, x, memory, src_mask, tgt_mask):
for layer in self.layers:
x = layer(x, memory, src_mask, tgt_mask)
return self.norm(x)最终,整个transformer完整模型的整体封装代码为
def make_model(src_vocab, tgt_vocab, N=6,
d_model=512, d_ff=2048, h=8, dropout=0.1):
"Helper: Construct a model from hyperparameters."
c = copy.deepcopy
attn = MultiHeadedAttention(h, d_model)
ff = PositionwiseFeedForward(d_model, d_ff, dropout)
position = PositionalEncoding(d_model, dropout)
model = EncoderDecoder(
Encoder(EncoderLayer(d_model, c(attn), c(ff), dropout), N),
Decoder(DecoderLayer(d_model, c(attn), c(attn),
c(ff), dropout), N),
nn.Sequential(Embeddings(d_model, src_vocab), c(position)),
nn.Sequential(Embeddings(d_model, tgt_vocab), c(position)),
Generator(d_model, tgt_vocab))
# This was important from their code.
# Initialize parameters with Glorot / fan_avg.
for p in model.parameters():
if p.dim() > 1:
nn.init.xavier_uniform(p)
return model
# Small example model.
tmp_model = make_model(10, 10, 2)
None2.3 编码器与解码器的协同
当我们把编码器和解码器组合到一起后,看下它两是如何一块协作的

需要注意的是
- Encoder中的Q、K、V全部来自于上一层单元的输出
而Decoder只有Q来自于上一个Decoder单元的输出,K与V都来自于Encoder最后一层的输出。也就是说,Decoder是要通过当前状态与Encoder的输出算出权重后(计算query与各个key的相似度),最后将Encoder的编码加权得到下一层的状态
比如当我们要把“Hello Word”翻译为“你好,世界”时
Decoder会计算“你好”这个query分别与“Hello”、“Word”这两个key的相似度
很明显,“你好”与“Hello”更相似,从而给“Hello”更大的权重,从而把“你好”对应到“Hello”,达到的效果就是“Hello”翻译为“你好” - 且在解码器中因为加了masked机制,自注意力层只允许关注已输出位置的信息,实现方法是在自注意力层的softmax之前进行mask,将未输出位置的权重设置为一个非常大的负数(进一步softmax之后基本变为0,相当于直接屏蔽了未输出位置的信息)
第三部分 Transformer的整个训练过程:预处理与迭代
3.1 预处理阶段:创建词汇表
具体实现时,先创建批次和掩码
class Batch:
def __init__(self, src, trg=None, pad=0):
self.src = src # 输入数据源(通常为源语言)
self.src_mask = (src != pad).unsqueeze(-2) # 创建源语言的掩码,用于忽略填充部分
if trg is not None: # 如果目标语言数据存在
self.trg = trg[:, :-1] # 目标语言数据,去掉最后一个词
self.trg_y = trg[:, 1:] # 目标语言数据,去掉第一个词
self.trg_mask = \
self.make_std_mask(self.trg, pad) # 创建目标语言的掩码,用于忽略填充部分和未来词汇
self.ntokens = (self.trg_y != pad).data.sum() # 计算目标语言中非填充词的数量
@staticmethod
def make_std_mask(tgt, pad):
"Create a mask to hide padding and future words."
tgt_mask = (tgt != pad).unsqueeze(-2) # 创建目标语言的掩码,用于忽略填充部分
tgt_mask = tgt_mask & Variable(
subsequent_mask(tgt.size(-1)).type_as(tgt_mask.data)) # 使用子掩码屏蔽未来词汇
return tgt_mask # 返回完整的目标语言掩码3.2 训练三部曲:随机初始化、损失函数、反向传播
接下来,我们创建一个通用的训练和得分函数来跟踪损失。我们传入一个通用的损失计算函数,它也处理参数更新
def run_epoch(data_iter, model, loss_compute):
start = time.time() # 记录当前时间
total_tokens = 0 # 初始化总tokens计数
total_loss = 0 # 初始化总损失
tokens = 0 # 初始化tokens计数
# 遍历数据集中的每个批次
for i, batch in enumerate(data_iter):
# 对每个批次进行前向传播
out = model.forward(batch.src, batch.trg,
batch.src_mask, batch.trg_mask)
# 计算每个批次的损失
loss = loss_compute(out, batch.trg_y, batch.ntokens)
# 累加损失
total_loss += loss
total_tokens += batch.ntokens # 累加tokens
tokens += batch.ntokens # 累加tokens
# 每50个批次进行一次日志记录
if i % 50 == 1:
elapsed = time.time() - start # 计算已用时间
# 输出当前批次,损失和每秒处理的tokens
print("Epoch Step: %d Loss: %f Tokens per Sec: %f" %
(i, loss / batch.ntokens, tokens / elapsed))
start = time.time() # 重置开始时间
tokens = 0 # 重置tokens计数
return total_loss / total_tokens # 返回平均损失下面这段代码定义了一个名为 SimpleLossCompute 的类,实现了简单的损失计算和训练函数
- 在调用该类的实例时,输入预测输出、目标输出和规范化因子,计算损失值并进行梯度更新
- 如果提供了优化器,还会更新模型参数和清空梯度缓存
# 定义 SimpleLossCompute 类,实现简单的损失计算和训练函数
class SimpleLossCompute:
# 初始化 SimpleLossCompute 类的实例
def __init__(self, generator, criterion, opt=None):
self.generator = generator # 生成器,用于预测输出
self.criterion = criterion # 损失函数,如交叉熵损失
self.opt = opt # 优化器,如 Adam
# 定义调用 SimpleLossCompute 类实例时的操作
def __call__(self, x, y, norm):
x = self.generator(x) # 生成预测输出
# 计算损失,这里需要将预测输出和目标输出转换为合适的形状
loss = self.criterion(x.contiguous().view(-1, x.size(-1)),
y.contiguous().view(-1)) / norm
loss.backward() # 计算梯度
if self.opt is not None: # 如果提供了优化器
self.opt.step() # 更新模型参数
self.opt.optimizer.zero_grad() # 清空梯度缓存
return loss.data[0] * norm # 返回损失值乘以规范化因子(实际损失值)3.2.1 Adam优化器:自动调整学习率并具有动量效应
优化器(optimizer)经常用于在训练过程中更新模型参数以最小化损失函数,而Adam(Adaptive Moment Estimation)是一种常用的优化器,它结合了两种传统优化算法的优点:Momentum和RMSprop
为了通俗易懂地理解Adam,可以将其比作一个赛车手。训练模型就像是找到一辆赛车在赛道上的最佳行驶速度和路径,以达到最快的速度并取得优异的成绩。在这个过程中,速度的调整(即学习率)非常重要
-
首先,Adam像Momentum一样,具有动量效应。这意味着赛车手(模型)会积累动量,使其在下坡时更快,而在上坡时减速。这有助于模型更快地穿越平坦区域,并避免在最低点附近摆动
-
其次,Adam像RMSprop一样,会自适应地调整每个参数的学习率。在我们的赛车比喻中,这就像赛车手会针对每个轮胎的摩擦系数(赛道状况)做出相应的速度调整。这有助于模型更快地收敛到最优解
总之,Adam可以自动调整学习率,并具有动量效应。总的来说,它能帮助我们的“赛车手”在不同的赛道状况下更快地找到最佳行驶速度和路径,从而更快地训练出高效的模型
transformer原始论文便选择的Adam作为优化器,其参数为,
和
,根据以下公式,我们在训练过程中改变了学习率:
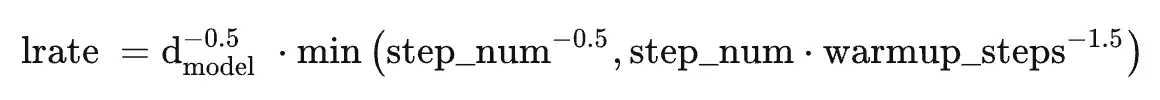
在预热中随步数线性地增加学习速率,并且此后与步数的反平方根成比例地减小它,设置预热步数为4000
我们来看下具体的编码实现。下面这段代码定义了一个名为 NoamOpt 的类,实现了一种自适应学习率调整策略,该策略在训练 Transformer 模型时常用。在训练的前几个步骤(预热期)中,学习率会线性增长,之后学习率会随着步数的增加而逐渐降低。这种策略有助于模型在训练初期更快地收敛,同时在训练后期保持较低的学习率,有利于模型的稳定训练。
# 定义 NoamOpt 类,实现自适应学习率调整策略
class NoamOpt:
# 初始化 NoamOpt 类的实例
def __init__(self, model_size, factor, warmup, optimizer):
self.optimizer = optimizer # 优化器对象(如 Adam)
self._step = 0 # 记录优化步数
self.warmup = warmup # 预热步数
self.factor = factor # 缩放因子
self.model_size = model_size # 模型维度大小
self._rate = 0 # 初始学习率
# 更新模型参数和学习率
def step(self):
self._step += 1 # 优化步数加 1
rate = self.rate() # 计算当前学习率
for p in self.optimizer.param_groups: # 更新优化器中的学习率
p['lr'] = rate
self._rate = rate # 存储当前学习率
self.optimizer.step() # 更新模型参数
# 计算当前步数的学习率
def rate(self, step=None):
if step is None: # 如果未提供步数,使用当前步数
step = self._step
return self.factor * \
(self.model_size ** (-0.5) * # 计算学习率公式中的模型维度项
min(step ** (-0.5), step * self.warmup ** (-1.5))) # 计算学习率公式中的最小值项
# 定义用于获取 NoamOpt 类实例的函数
def get_std_opt(model):
return NoamOpt(model.src_embed[0].d_model, 2, 4000,
torch.optim.Adam(model.parameters(), lr=0, betas=(0.9, 0.98), eps=1e-9))最后总结一下Transformer的影响力
- OpenAI基于它发展出了GPT,并不断迭代出GPT2、GPT3、GPT3.5及火爆全球的 ChatGPT
- Google则基于它发展出了在ChatGPT出现之前统治NLP各大任务的BERT,多好的青春年华!
第四部分 ChatGLM-6B的代码架构与逐一实现
ChatGLM-6B(介绍页面、代码地址),是智谱 AI 开源、支持中英双语的对话语言模型。
话不多说,直接干,虽然6B的版本相比GPT3 175B 不算大,但毕竟不是一个小工程,本文就不一一贴所有代码了,更多针对某个文件夹下或某个链接下的代码进行整体分析/说明,以帮助大家更好、更快的理解ChatGLM-6B,从而加速大家的类ChatGPT复现之路
4.1 chatglm-6b/modeling_chatglm.py(本节正在整理完善中,预计4.20日ok)
4.1.1 导入相关库、编码器、GELU、旋转位置编码(第1-239行)
- 首先,代码导入了许多需要的库,如torch、torch.nn.functional等,它们为模型实现提供了基本的功能。
脚本中设置了一些标志,以便在运行时启用JIT(Just-In-Time)编译功能 - 定义了InvalidScoreLogitsProcessor类,它继承自LogitsProcessor。该类用于处理可能出现的NaN和inf值,通过将它们替换为零来确保计算的稳定性
- load_tf_weights_in_chatglm_6b函数,用于从TensorFlow检查点加载权重到PyTorch模型中。这对于迁移学习和在PyTorch中使用预训练模型非常有用
- PrefixEncoder类是一个编码器,用于对输入的前缀进行编码。它根据配置使用一个两层的MLP(多层感知器)或者直接进行嵌入,输出维度为(batch_size, prefix_length, 2 * layers * hidden)
- gelu_impl函数是一个GELU(高斯误差线性单元)激活函数的实现,这是一个常用的激活函数,尤其在Transformer模型中
# 使用PyTorch的JIT编译器,将Python函数转换为Torch脚本,以便优化和加速执行 @torch.jit.script # 定义名为gelu_impl的函数,接受一个参数x def gelu_impl(x): # 返回GELU激活函数的计算结果,这里使用了一种近似计算方法 return 0.5 * x * (1.0 + torch.tanh(0.7978845608028654 * x * (1.0 + 0.044715 * x * x))) # 定义名为gelu的函数,接受一个参数x def gelu(x): # 调用gelu_impl函数并返回结果 return gelu_impl(x)
- RotaryEmbedding类实现了旋转位置编码(第177-239行)。旋转位置编码是一种新型的位置编码方法,相比于传统的位置编码,它在大序列长度和多头注意力上具有更好的性能
_load_from_state_dict方法:这是一个空方法,用于从给定的状态字典加载模型参数。在这个代码段中,它没有实现任何功能
forward方法:这是一个核心方法,实现了正向传播,输入为x和可选参数seq_dim和seq_len。这个方法首先计算序列长度,然后根据条件更新max_seq_len_cached。接着,它计算嵌入向量,并将其缓存。最后,它返回余弦和正弦缓存
# 类的前向传播方法,接收三个参数 def forward(self, x, seq_dim=1, seq_len=None): # 如果没有提供序列长度,则从输入张量的形状中获取序列长度 if seq_len is None: seq_len = x.shape[seq_dim] # 如果缓存的最大序列长度不存在,或者提供的序列长度大于缓存的最大序列长度 if self.max_seq_len_cached is None or (seq_len > self.max_seq_len_cached): # 更新缓存的最大序列长度 self.max_seq_len_cached = None if self.learnable else seq_len # 创建等差序列 t = torch.arange(seq_len, device=x.device, dtype=self.inv_freq.dtype) # 计算频率张量 freqs = torch.einsum('i,j->ij', t, self.inv_freq) # 将频率张量沿最后一个维度进行拼接,形成旋转嵌入 emb = torch.cat((freqs, freqs), dim=-1).to(x.device) # 如果精度为bfloat16,将旋转嵌入转换为float类型 if self.precision == torch.bfloat16: emb = emb.float() # 计算旋转嵌入的余弦值和正弦值,形状为 [sx, 1 (b * np), hn] cos_cached = emb.cos()[:, None, :] sin_cached = emb.sin()[:, None, :] if self.precision == torch.bfloat16: # 如果精度为bfloat16,将余弦值转换为bfloat16类型 cos_cached = cos_cached.bfloat16() # 如果精度为bfloat16,将正弦值转换为bfloat16类型 sin_cached = sin_cached.bfloat16() # 如果旋转嵌入是可学习的 if self.learnable: # 返回余弦值和正弦值 return cos_cached, sin_cached # 更新缓存的余弦值和正弦值 self.cos_cached, self.sin_cached = cos_cached, sin_cached # 返回截取后的余弦值和正弦值,以匹配输入序列的长度 return self.cos_cached[:seq_len, ...], self.sin_cached[:seq_len, ...]_apply方法:这个方法应用给定的函数(fn)到缓存的余弦和正弦值上,并调用父类的_apply方法
rotate_half函数:这个函数将输入张量x在最后一个维度上分为两半,并将它们交换位置
apply_rotary_pos_emb_index函数:这个函数应用了旋转位置嵌入索引,主要通过cos和sin将位置信息添加到输入张量q和k上
# 使用PyTorch的JIT编译器,将Python函数转换为Torch脚本,以便优化和加速执行 @torch.jit.script # 定义一个名为apply_rotary_pos_emb_index的函数,接收五个参数 def apply_rotary_pos_emb_index(q, k, cos, sin, position_id): # 通过position_id获取cos和sin的嵌入表示 # cos.squeeze(1)和sin.squeeze(1)用于去除多余的维度 # 而unsqueeze(2)则用于重新添加所需的维度 # 从而将cos和sin的形状从[sq, 1, hn]变为[sq, b, np, hn],以便后续q和k进行运算 cos, sin = F.embedding(position_id, cos.squeeze(1)).unsqueeze(2), \ F.embedding(position_id, sin.squeeze(1)).unsqueeze(2) # 计算旋转位置编码后的q和k,将q和k与cos和sin进行点积运算 q, k = (q * cos) + (rotate_half(q) * sin), (k * cos) + (rotate_half(k) * sin) # 返回旋转位置编码后的q和k return q, k
4.1.2 SelfAttention的PyTorch模块:实现自注意力机制(第242-658行)
定义了一个名为SelfAttention的PyTorch模块,它实现了自注意力机制。这个模块在许多自然语言处理任务中都被用作基本构建块。以下是代码中的关键部分:
- attention_fn方法:这个方法实现了自注意力的核心计算过程,包括计算注意力分数、注意力概率和上下文层。这些计算对于实现许多自然语言处理任务,如语言建模、命名实体识别等,都是非常重要的
为方便大家更好、更快、更一目了然的理解,我花了个把钟头,一如上面的 依然把下面每一行代码都逐行加上了注释,且关键的部分加了额外的解释说明# 定义attention函数 def attention_fn( self, query_layer, # 查询层张量 key_layer, # 键层张量 value_layer, # 值层张量 attention_mask, # 注意力掩码张量 hidden_size_per_partition, # 每个分区的隐藏层大小,每个分区可能包含2或4或8个头 layer_id, # 当前层的ID layer_past=None, # 保存过去的键和值的张量,用于解码器的自回归任务 scaling_attention_score=True, # 是否缩放注意力分数,默认为True use_cache=False, # 是否使用缓存,默认为False ): # 如果layer_past不为空,则获取然后拼接过去的key和value if layer_past is not None: past_key, past_value = layer_past[0], layer_past[1] key_layer = torch.cat((past_key, key_layer), dim=0) value_layer = torch.cat((past_value, value_layer), dim=0) # 获取key_layer的形状信息 # 包括序列长度sq、批大小b、注意力头数(np,原代码为nh,应该是笔误)、每个注意力头的隐藏层大小hn seq_len, b, nh, hidden_size = key_layer.shape # 如果使用缓存,则设置present为key和value的元组,否则为None if use_cache: present = (key_layer, value_layer) else: present = None # 计算查询-键层缩放系数 query_key_layer_scaling_coeff = float(layer_id + 1) # 如果需要缩放注意力分数,对查询层进行缩放 if scaling_attention_score: query_layer = query_layer / (math.sqrt(hidden_size) * query_key_layer_scaling_coeff) # 设置输出张量的大小,计算原始注意力分数的形状:[b, np, sq, sk] output_size = (query_layer.size(1), query_layer.size(2), query_layer.size(0), key_layer.size(0)) """ 解释下:query_layer 的原始形状为 [seqlen, batch,num_attention_heads,hidden_size_per_attention_head],简写为[sq,b,np,hn] 故query_layer.size(1)对应b, query_layer.size(2)对应np, query_layer.size(0)对应sq key_layer 的原始形状为 [seklen,batch,num_attention_heads,hidden_size_per_attention_head],简写为[sk,b,np,hn] 所以key_layer.size(0)对应sk """ # 通过之前第39行的output_size[b, np, sq, sk],重塑查询层和键层张量 好进行矩阵相乘 # [sq, b, np, hn] -> [sq, b * np, hn] query_layer = query_layer.view(output_size[2], output_size[0] * output_size[1], -1) # [sk, b, np, hn] -> [sk, b * np, hn] key_layer = key_layer.view(output_size[3], output_size[0] * output_size[1], -1) """ 上面那两行再解释下,因为需要计算每个批次中每个注意力头的注意力分数,为此 将批次大小(batch)和注意力头数量(num_attention_heads)合并到一个维度中以便于执行矩阵乘法 因此,我们将 query_layer 的形状从[sq,b,np,hn]调整为 [sq, b * np, hn] 同理,对于 key_layer,将 key_layer 的形状从[sk,b,np,hn]调整为 [sk, b * np, hn] """ # 初始化乘法结果张量 matmul_result = torch.zeros( 1, 1, 1, dtype=query_layer.dtype, device=query_layer.device, ) # 计算查询层和键层的乘积 matmul_result = torch.baddbmm( matmul_result, # 将 query_layer 的形状从 [sq, b * np, hn] 转换为 [b * np, sq, hn] query_layer.transpose(0, 1), # 将 key_layer 的形状从 [sk, b * np, hn] 转换为 [b * np, hn, sk] # 相当于对key_layer 进行了两次转置操作,得到形状为 [b * np, hn, sk] 的张量 key_layer.transpose(0, 1).transpose(1, 2), beta=0.0, alpha=1.0, ) # 上面最终query_layer为[b * np, sq, hn] # 上面最终key_layer 为[b * np, hn, sk] # 现在,沿用之前第39行的output_size的注意力分数张量[b, np, sq, sk] attention_scores = matmul_result.view(*output_size) # 使用缩放掩码Softmax计算注意力概率 if self.scale_mask_softmax: self.scale_mask_softmax.scale = query_key_layer_scaling_coeff attention_probs = self.scale_mask_softmax(attention_scores, attention_mask.contiguous()) else: # 如果掩码不全为0,应用注意力掩码 if not (attention_mask == 0).all(): attention_scores.masked_fill_(attention_mask, -10000.0) # 转换注意力分数张量的数据类型为浮点数 dtype = attention_scores.dtype attention_scores = attention_scores.float() # 缩放注意力分数 attention_scores = attention_scores * query_key_layer_scaling_coeff # 对注意力分数执行Softmax操作以获取注意力概率 attention_probs = F.softmax(attention_scores, dim=-1) # 将注意力概率张量的数据类型恢复为原始数据类型 attention_probs = attention_probs.type(dtype) """ 计算上下文层[sq, b, hp] """ # 对原始value_layer做下转换得到新的output_size:[sk, b, np, hn] --> [b, np, sq, hn] output_size = (value_layer.size(1), value_layer.size(2), query_layer.size(0), value_layer.size(3)) # 对原始value_layer的中间两个维度做下合并 [sk, b, np, hn] -> [sk, b * np, hn] value_layer = value_layer.view(value_layer.size(0), output_size[0] * output_size[1], -1) # 调整注意力概率:对之前得到的前两个维度做下合并:[b, np, sq, sk] =》[b * np, sq, sk] attention_probs = attention_probs.view(output_size[0] * output_size[1], output_size[2], -1) # 对上一行得到的attention_probs[b * np, sq, sk] # 乘以『value_layer即[sk, b * np, hn]的转置』,即[b * np, hn, sk] # 相当于[b * np, sq, sk] x [b * np, hn, sk],最终得到[b * np, sq, hn] context_layer = torch.bmm(attention_probs, value_layer.transpose(0, 1)) # 上行得到context_layer的[b * np, sq, hn]通过上面第116行的新output_size调整为4个维度的 # [b, np, sq, hn] # 使其更直观地表示批量大小b、注意力头数np、查询序列长度sq以及每个注意力头的隐藏层大小hn context_layer = context_layer.view(*output_size) # [b, np, sq, hn] --> [sq, b, np, hn],使其与查询层(query_layer)的形状一致 context_layer = context_layer.permute(2, 0, 1, 3).contiguous() # [sq, b, np, hn] --> [sq, b, hp],此举的作用在于前两个维度(sq 和 b)不变 # 同时将后两个维度(np 和 hn)合并成单个维度,即每个分区的隐藏层大小(hp) new_context_layer_shape = context_layer.size()[:-2] + (hidden_size_per_partition,) context_layer = context_layer.view(*new_context_layer_shape) # 将上下文层、当前的键值对(present)以及注意力概率(attention_probs)打包成一个元组 outputs = (context_layer, present, attention_probs) return outputs - default_init函数:这个函数是一个初始化辅助函数,用于创建类的实例。
SelfAttention类定义:这个类实现了自注意力机制,包括定义类的初始化方法和成员变量。类的初始化方法包括设置各种属性,如hidden_size,num_attention_heads,layer_id等。类还包含一个名为rotary_emb的RotaryEmbedding实例,用于处理位置编码。此外,query_key_value和dense是用于计算查询、键和值的线性层。
- attention_mask_func方法,将注意力掩码应用于Transformer模型中的注意力得分(到了第407行)
@staticmethod def attention_mask_func(attention_scores, attention_mask): # 使用掩码 (attention_mask) 更新注意力得分 (attention_scores) # 对于掩码值为0的位置,将注意力得分设置为-10000.0 attention_scores.masked_fill_(attention_mask, -10000.0) # 返回更新后的注意力得分张量 return attention_scores - split_tensor_along_last_dim 方法
该方法沿着张量的最后一个维度将其分割成多个部分。参数包括输入张量 tensor、要将张量分割成的分区数 num_partitions,以及布尔值 contiguous_split_chunks,用于确定分割后的张量是否需要在内存中连续。函数首先计算最后一个维度的大小,然后使用torch.split将输入张量分割成多个子张量。如果需要连续的分割块,将每个子张量转换为连续张量 - SelfAttention 类的 forward 方法:
该方法负责计算自注意力。它接收以下参数:hidden_states(输入序列的隐藏状态)、position_ids(位置编码)、attention_mask(注意力掩码)、layer_id(层ID)、layer_past(上一层的隐藏状态),以及use_cache(布尔值,表示是否使用缓存)和output_attentions(布尔值,表示是否输出注意力概率)。方法首先将隐藏状态传递给查询键值 (query, key, value) 层,然后将这些层分割成独立的张量。接下来,应用旋转位置编码,计算注意力概率,并得到上下文表示。最后,返回输出张量、隐藏状态以及注意力概率(如果需要的话)。
4.1.3 GLMBlock类、ChatGLMPreTrainedModel类
GLMBlock 类:这是一个包含多个子模块的Transformer层,如层归一化 (LayerNorm)、自注意力 (SelfAttention) 和门控线性单元 (GLU)。GLMBlock 类的 forward 方法接收与SelfAttention的forward方法类似的参数,如输入序列的隐藏状态、位置编码、注意力掩码等。在这个方法中,首先应用层归一化,然后计算自注意力,接着应用第二个层归一化,最后通过门控线性单元 (GLU) 计算输出。在每个步骤之间,都有残差连接来保留之前的信息。最后,返回输出张量、隐藏状态以及注意力概率(如果需要的话)。
接下来第661-729行,定义了一个名为 ChatGLMPreTrainedModel 的类,它继承自 PreTrainedModel。这个类是用于处理权重初始化以及简化下载和加载预训练模型的接口。
- 类变量包括:
is_parallelizable:表示该模型是否可并行化,默认为 False
supports_gradient_checkpointing:表示该模型是否支持梯度检查点,默认为 True
config_class:模型配置类,这里使用了 ChatGLMConfig
base_model_prefix:设置为 “transformer”
_no_split_modules:一个包含 “GLMBlock” 的列表 - 类方法包括:
__init__:构造函数,调用父类的构造函数
_init_weights:初始化权重的方法,这里没有具体实现
get_masks:根据输入生成注意力掩码
get_position_ids:根据输入和掩码位置生成位置编码,支持二维和非二维位置编码
_set_gradient_checkpointing:根据给定的值(默认为False)设置梯度检查点。
此外,还定义了一个名为 CHATGLM_6B_START_DOCSTRING 的变量,包含有关 ChatGLM6BConfig 的文档字符串,描述了如何使用这个 PyTorch 模型。
4.1.4 ChatGLMModel类(第731-1029行)
定义了一个名为ChatGLMModel的类,它继承自ChatGLMPreTrainedModel。这是一个基于transformer的模型,能够作为编码器(仅使用自注意力机制)或解码器。解码器的情况下,会在自注意力层之间添加一个跨注意力层。模型的结构遵循论文Attention is all you need中描述的结构。
ChatGLMModel类的forward方法负责执行模型的前向传播。这个方法接收一系列输入参数,如input_ids、attention_mask、past_key_values等。根据这些输入,方法将执行以下操作:
- 如果没有提供inputs_embeds,使用word_embeddings将input_ids转换为嵌入向量
- 如果没有提供past_key_values,使用get_prompt方法获取提示
- 如果没有提供attention_mask,生成一个全零的张量
- 如果没有提供position_ids,使用get_position_ids方法获取位置ID
- 使用注意力掩码更新输入
- 对于模型中的每个层,执行以下操作:
更新隐藏状态
如果需要,保存当前层的隐藏状态
更新注意力权重 - 对最后一层应用层归一化。
- 如果需要,保存所有隐藏状态。
- 如果需要,返回一个包含所有输出的元组,否则返回一个BaseModelOutputWithPast对象。
这个模型的设计可以在序列到序列(Seq2Seq)任务中使用,这时需要将is_decoder和add_cross_attention参数设置为True,并在前向传播时提供encoder_hidden_states。
4.1.5 ChatGLMForConditionalGeneration的类(第1032-1437行)
定义了一个名为ChatGLMForConditionalGeneration的类,,它用于条件生成任务,如文本生成。这个类继承自ChatGLMPreTrainedModel,主要包括初始化方法、模型的前向传播逻辑以及生成过程中需要的输入预处理方法。
主要部分的解释如下:
- __init__方法是类的构造函数,用于初始化该类的实例。它接受两个参数:config(一个ChatGLMConfig实例,包含模型的配置信息)和empty_init(一个布尔值,表示是否跳过模型参数的初始化)。构造函数首先调用父类的构造函数,然后根据empty_init的值选择初始化方法。接着,它初始化一些实例变量,例如max_sequence_length和position_encoding_2d。最后,它初始化transformer和lm_head两个关键组件
- get_output_embeddings和set_output_embeddings方法分别用于获取和设置lm_head的权重。
- _update_model_kwargs_for_generation方法用于在生成过程中更新模型的关键字参数,包括更新past_key_values、attention_mask和position_ids。
- prepare_inputs_for_generation方法在生成过程中准备模型的输入,包括input_ids、past_key_values、attention_mask和position_ids等。此外,该方法还处理了遮罩位置和gmask的使用。
- forward方法实现了模型的前向传播逻辑。它接受一系列可选参数,例如input_ids、position_ids、attention_mask、past_key_values等,并根据这些输入调用transformer模块。接着,它将hidden_states传递给lm_head,并计算lm_logits。如果提供了标签(labels),则计算损失函数。最后,根据return_dict的值,返回一个包含损失、logits、隐藏状态等信息的元组或字典。此时到了1231行
- _reorder_cache 方法:在执行束搜索 (beam search) 或者束采样 (beam sample) 时用于重新排序 past_key_values 缓存,以便将 past_key_values 与正确的 beam_idx 匹配。
- process_response 方法:处理模型生成的回应,将其中的训练时间替换为 “2023年”,同时将英文标点符号替换为中文标点符号。
- chat 方法:根据给定的查询和聊天历史生成回应。通过 tokenizer 对查询和聊天历史进行编码,并将其输入到模型中。然后,对模型生成的回应进行解码和处理,最后将新的回应添加到聊天历史中并返回。
- stream_chat 方法:与 chat 方法类似,但使用生成器函数 (generator function) 以流式方式生成回应。
- stream_generate 方法:一个生成器函数,用于生成回应。它首先将输入的 query 和聊天历史进行编码,然后根据生成配置 (generation_config) 进行一系列的准备工作。接着,在满足停止条件之前,通过模型的多次迭代来生成回应。
- quantize 方法:量化模型的权重,以减少模型的内存占用和计算资源。这对于在资源有限的设备上部署模型非常有用。
该类中还包括一些辅助方法,例如 _get_logits_processor, _get_stopping_criteria, _get_logits_warper, prepare_inputs_for_generation, 和 _update_model_kwargs_for_generation,这些方法用于处理生成过程中的各种设置和参数。
第五部分 如何加速模型的训练以及调优
// 待5月份补充
参考文献与推荐阅读
- Transformer通俗笔记:从Word2Vec、Seq2Seq逐步理解到GPT、BERT
- Transformer原始论文(值得反复读几遍):Attention Is All You Need
- Vision Transformer 超详细解读 (原理分析+代码解读) (一)
- Transformer模型详解(图解最完整版)
- The Annotated Transformer(翻译之一),harvard对transformer的简单编码实现
- transformer的细节到底是怎么样的?
- 如何从浅入深理解transformer?
- Transformer 结构详解:位置编码 | Transformer Architecture: The Positional Encoding
- Transformer学习笔记一:Positional Encoding(位置编码)
- 保姆级讲解Transformer
- Jay Alammar写的图解transformer
- 如何理解attention中的Q,K,V?
附录:创作/修改记录
- 4.12-4.14,基本完成第一部分 transformer编码器部分的初稿
- 4.16,彻底完善关于transformer位置编码的阐述,可能是网上对这点最一目了然的阐述了
- 4.17,完成transformer的解码器部分
- 4.18,开始写「第四部分 ChatGLM-6B的代码架构与逐一实现」
文章出处登录后可见!