Kruskal算法

前置知识：并查集、图的存储、贪心思想

为了保证学习效果，请保证已经掌握前置知识之后，再来学习本章节！如果在阅读中遇到困难，也可以回到前面章节查阅。

克鲁斯卡尔算法(Kruskal算法)

适用于稀疏图，时间复杂度 O(mlogm)O(mlogm)。

核心思想：从小到大挑不多余的边，属于贪心的算法。

之前介绍了求最小生成树之普里姆算法。该算法从顶点的角度为出发点，时间复杂度为O(n^2)O(n2)，更适合与解决边的绸密度更高的连通网。

本节所介绍的克鲁斯卡尔算法，从边的角度求网的最小生成树，时间复杂度为O(E\log E)O(ElogE)。和普里姆算法恰恰相反，更适合于求边稀疏的网的最小生成树。

对于任意一个连通网的最小生成树来说，在要求总的权值最小的情况下，最直接的想法就是将连通网中的所有边按照权值大小进行升序排序，从小到大依次选择。

由于最小生成树本身是一棵生成树，所以需要时刻满足以下两点：

• 生成树中任意顶点之间有且仅有一条通路，也就是说，生成树中不能存在回路；
• 对于具有 n 个顶点的连通网，其生成树中只能有 n-1 条边，这 n-1 条边连通着 n 个顶点。

连接 n 个顶点在不产生回路的情况下，只需要 n-1 条边。

思路

所以克鲁斯卡尔算法的具体思路是：将所有边按照权值的大小进行升序排序，然后从小到大一一判断，条件为：如果这个边不会与之前选择的所有边组成回路，就可以作为最小生成树的一部分；反之，舍去。直到具有 n 个顶点的连通网筛选出来 n-1 条边为止。筛选出来的边和所有的顶点构成此连通网的最小生成树。

判断是否会产生回路的方法为：在初始状态下给每个顶点赋予不同的标记，对于遍历过程的每条边，其都有两个顶点，判断这两个顶点的标记是否一致，如果一致，说明它们本身就处在一棵树中，如果继续连接就会产生回路；如果不一致，说明它们之间还没有任何关系，可以连接。

过程

假设遍历到一条由顶点 A 和 B 构成的边，而顶点 A 和顶点 B 标记不同，此时不仅需要将顶点 A 的标记更新为顶点 B 的标记，还需要更改所有和顶点 A 标记相同的顶点的标记，全部改为顶点 B 的标记。

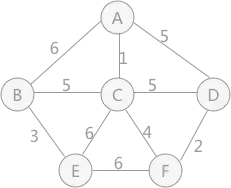
图 1 连通网

例如，使用克鲁斯卡尔算法找图 1 的最小生成树的过程为：

首先，在初始状态下，对各顶点赋予不同的标记（用颜色区别），如下图所示：

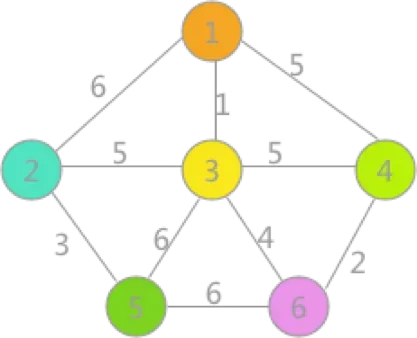
（1）

对所有边按照权值的大小进行排序，按照从小到大的顺序进行判断，首先是（1，3），由于顶点 1 和顶点 3 标记不同，所以可以构成生成树的一部分，遍历所有顶点，将与顶点 3 标记相同的全部更改为顶点 1 的标记，如（2）所示：

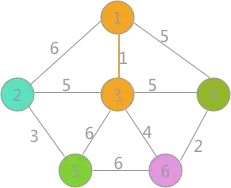
（2）

其次是（4，6）边，两顶点标记不同，所以可以构成生成树的一部分，更新所有顶点的标记为：

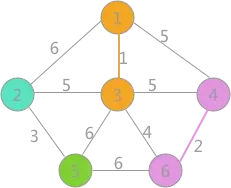
（3）

其次是（2，5）边，两顶点标记不同，可以构成生成树的一部分，更新所有顶点的标记为：

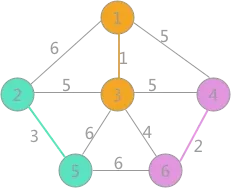
（4）

然后最小的是（3，6）边，两者标记不同，可以连接，遍历所有顶点，将与顶点 6 标记相同的所有顶点的标记更改为顶点 1 的标记：

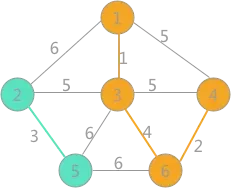
（5）

继续选择权值最小的边，此时会发现，权值为 5 的边有 3 个，其中（1，4）和（3，4）各自两顶点的标记一样，如果连接会产生回路，所以舍去，而（2，3）标记不一样，可以选择，将所有与顶点 2 标记相同的顶点的标记全部改为同顶点 3 相同的标记：

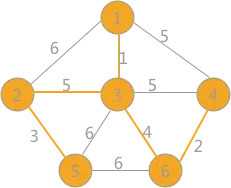
（6）

当选取的边的数量相比与顶点的数量小 1 时，说明最小生成树已经生成。所以最终采用克鲁斯卡尔算法得到的最小生成树为（6）所示。

示例代码

#include <bits/stdc++.h>
using namespace std;

const int N = 1e5+5;
int n, m, ans, cnt, fa[N];

struct Edge{
    int u, v, w;
} a[N*4];
bool cmp(Edge x, Edge y) {
    return x.w < y.w;
}
int find(int x) {
    if(x == fa[x]) return x;
    return fa[x] = find(fa[x]);
}
int main(){
    cin >> n >> m;
    for(int i = 1; i <= m; i++) {
        cin >> a[i].u >> a[i].v >> a[i].w;
    }
    for(int i = 1; i <= n; i++)
        fa[i] = i;
    sort(a+1, a+m+1, cmp);
    for(int i = 1; i <= m; i++) {
        int u = find(a[i].u), v = find(a[i].v);
        if(u == v) continue;
        fa[u] = v;
        cnt++;
        ans += a[i].w;
        if(cnt == n-1) {
            break;
        }
    }
    if(cnt == n-1) cout << ans;
    else cout << "impossible";
    return 0;
}

Copy

算法证明

原图 G=(V,E)G=(V,E)，其中，VV 为点集，EE 为边集。

我们在 EE 中找到边权最小的边，记为 e_{min} = (u,v)emin​=(u,v)，选择 uu 从 VV 中剔除，并记 eses 为所有和 uu 连接的边集， V’=V-uV′=V−u，E’=E-esE′=E−es，记。

经过上面处理，我们得到一个删除了结点 uu 的结点数减少了的新图 G’=(V’,E’)G′=(V′,E′)。

很明显，如果要把 uu 连到 G’G′ 上，从 eses 中任意选一条边加入，均不会形成环，那么，选择 e_{min}emin​ 必然是最优的。

如此，在 GG 上求最小生成树的问题就可以拆成两步解决：

1. 在 G’G′ 求最小生成树（和原问题相似，规模更小）
2. 如此就把原规模为 NN 的问题降为规模为 N-1N−1 的问题，而该问题和原问题相似，规模更小，如此反复处理，直至 N=1N=1 即可，把这个过程中选择的边合并即构成原图的最小生成树。

时间复杂度分析

排序：O(E\log E)O(ElogE)，采用并查集选边合并：O(E\alpha (V))O(Eα(V))，总时间复杂度：O(E\log E)O(ElogE)