博弈论-策略式博弈矩阵、扩展式博弈树 习题 [HBU]

目录

前言：

题目与求解

11.请将“田忌赛马”的博弈过程用策略式（博弈矩阵）和扩展式（博弈树）分别进行表示，并用文字分别详细表述。

34.两个朋友在一起划拳喝酒，每个人有4个纯策略：杠子、老虎、鸡和虫子。 输赢规则是：杠子降老虎，老虎降鸡，鸡降虫子，虫子降杠子。两个人同时出令，如果一方打败另一方，赢者的得益为1，输者的得益为-1，否则得益为0. 请给出以上博弈的策略式描述并求出所有的纳什均衡。

42.乙向甲索要1000元，并且威胁甲如果不给就与他同归于尽。当然，甲不一定会相信乙的威胁。 请用扩展式表示该博弈，并找出其子博弈完美纳什均衡。

前言：

本篇博客解决一些博弈论题目，题号已标清。

题目来自河北大学王亮老师的网址：Software Security Lab, Hebei University (hbusoftsec.org.cn)

题目与求解

题号：11  分值：20分

11.请将“田忌赛马”的博弈过程用策略式（博弈矩阵）和扩展式（博弈树）分别进行表示，并用文字分别详细表述。

假设田忌和齐王赛马，每人有上、中、下三个等级的马各一匹，上等马优于中等马，中等马优于下等马，同一等级的马中齐王的马优于田忌的马。比赛共进行三局，每匹马只能参加一局比赛，每局的胜者得1分，负者得-1分，比赛结果为三局得分之和。

玩家N=2： 田忌  齐王

策略集: {上中下、上下中、中上下、中下上、下上中、下中上}

(1)策略式博弈矩阵为：

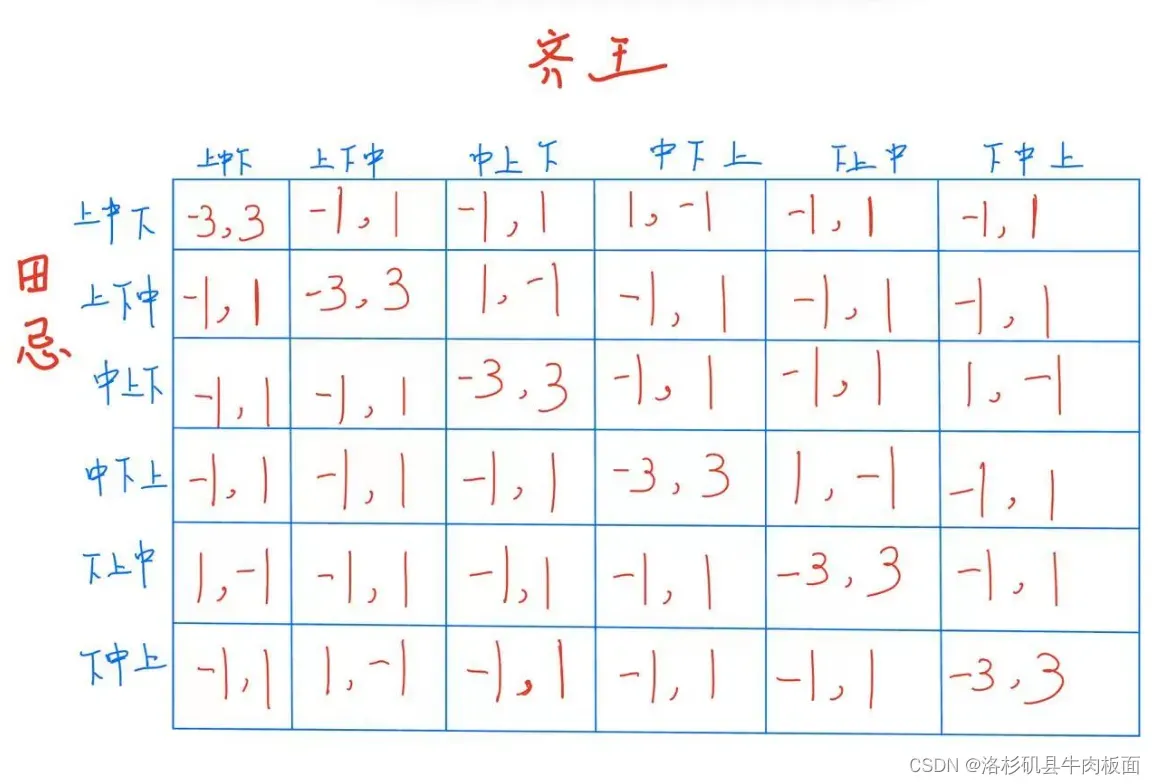
博弈矩阵中的每组数表示：左边的是田忌的得益，右边的是齐王的得益。

(2)扩展式(博弈树)为：

动态博弈的结果包括双方采用的策略组合、实现的博弈路径和各博弈方的得益。

这是一棵很大的树，为了可以看清楚每个分支，我拆分为三个部分展示：齐王先手-上，齐王先手-中，齐王先手-下。

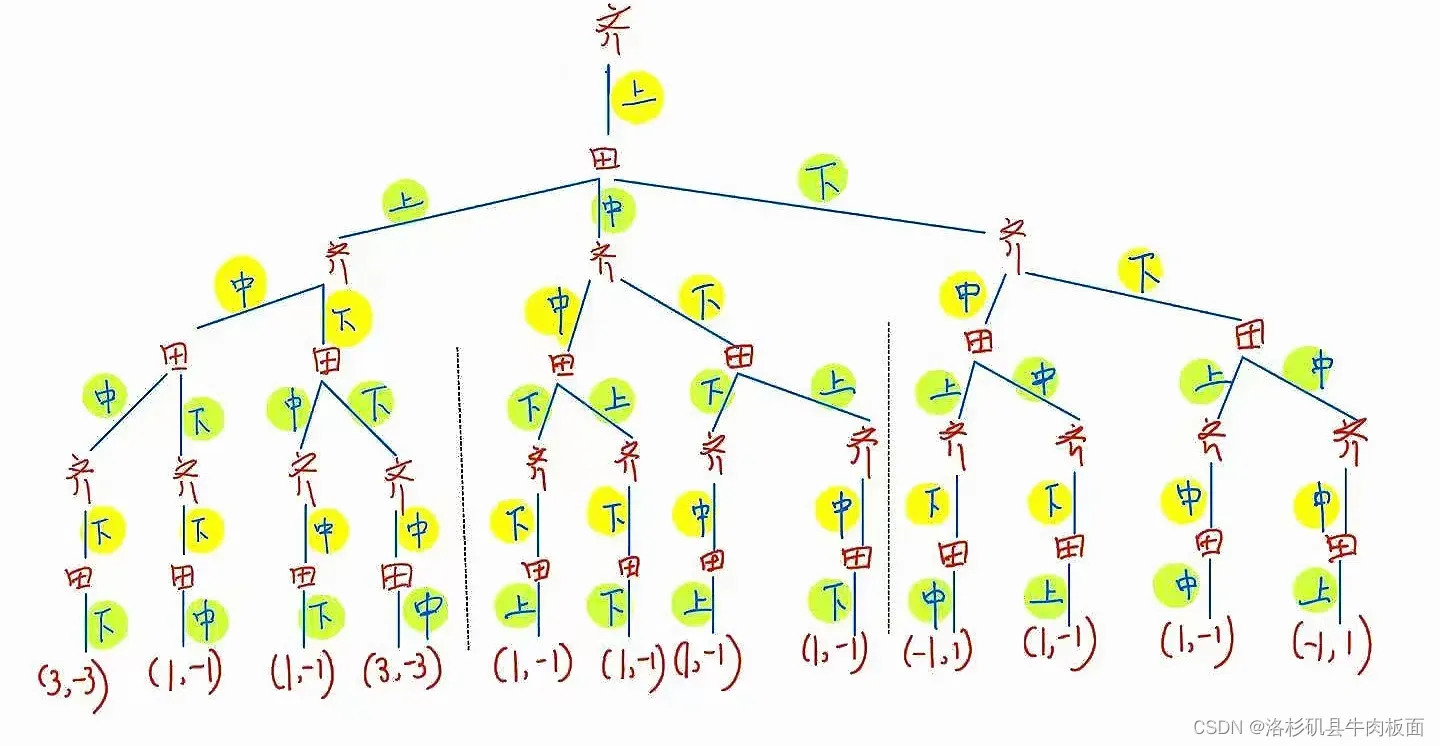
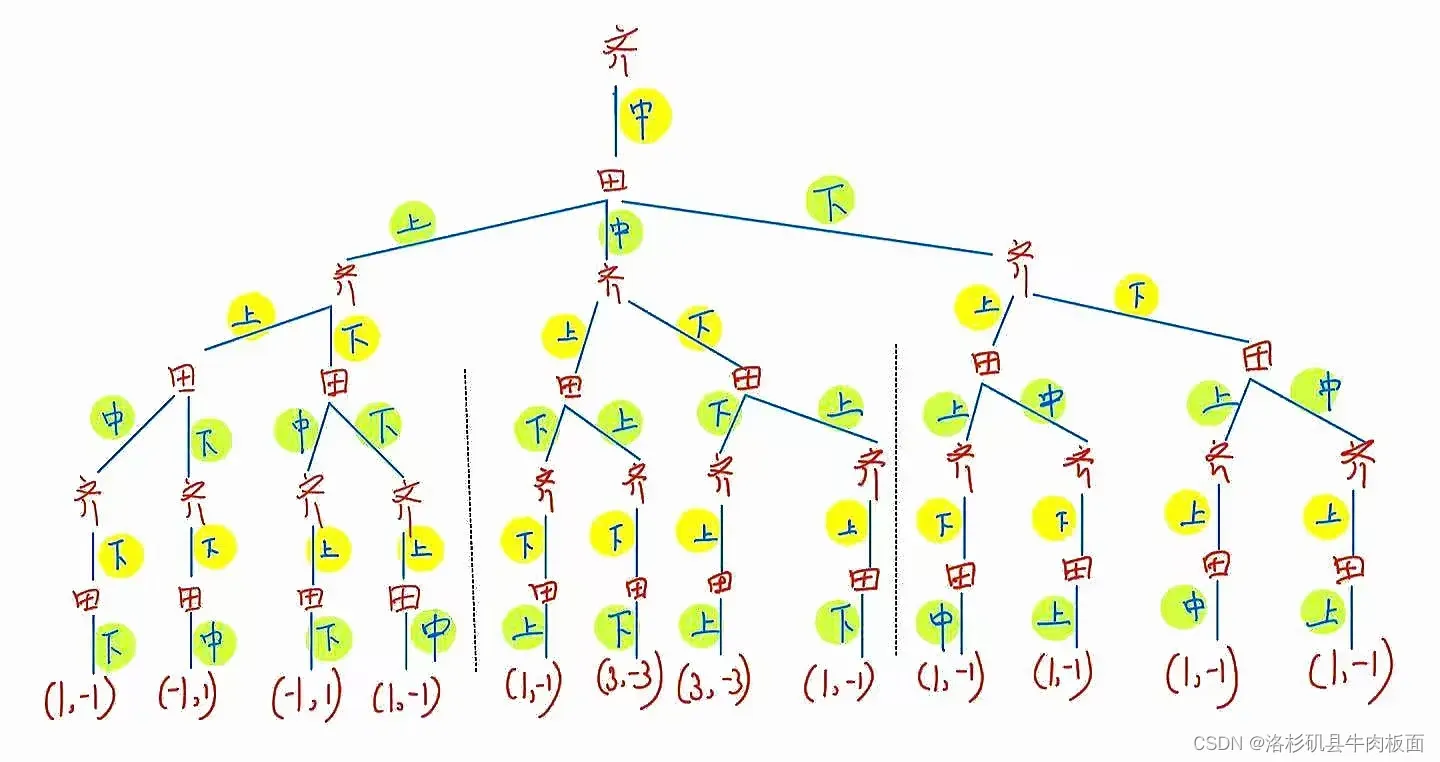
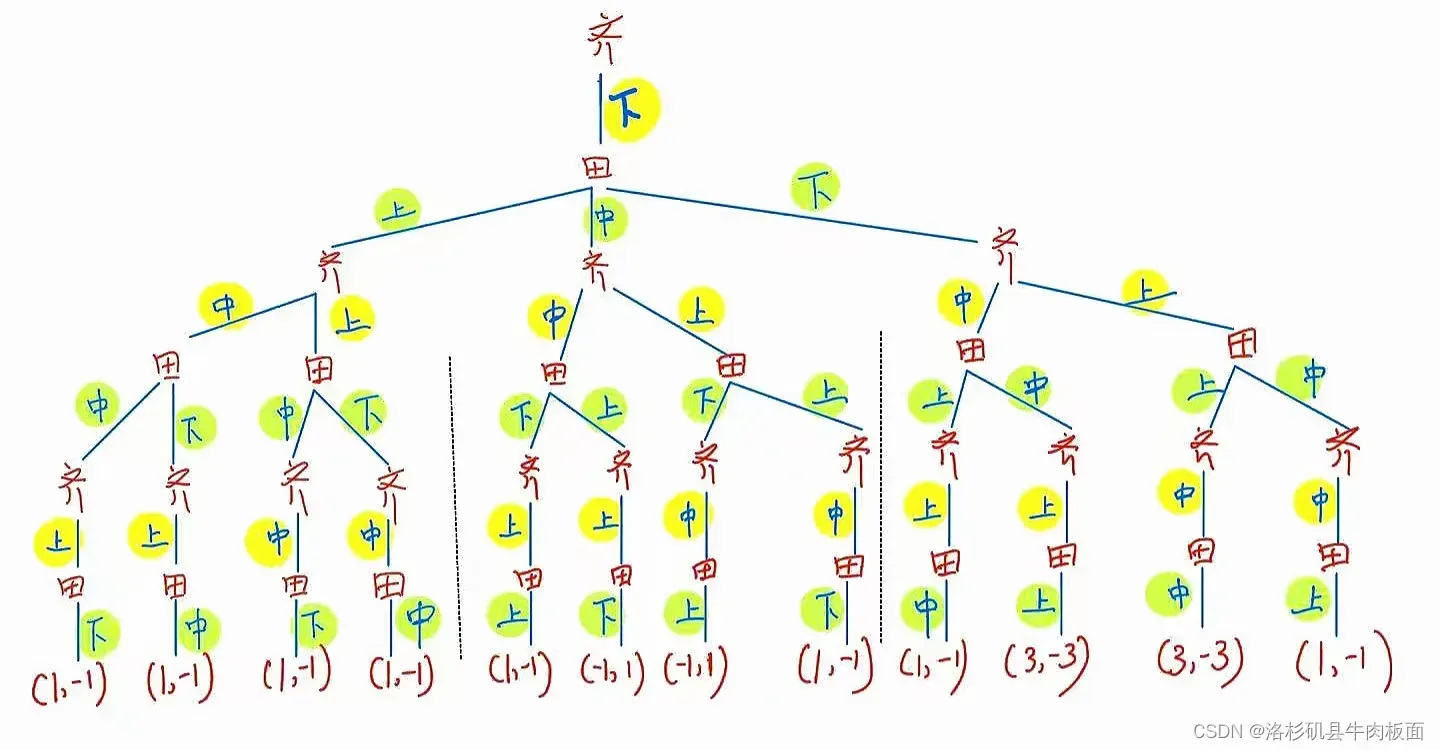
最后合并为一整棵树：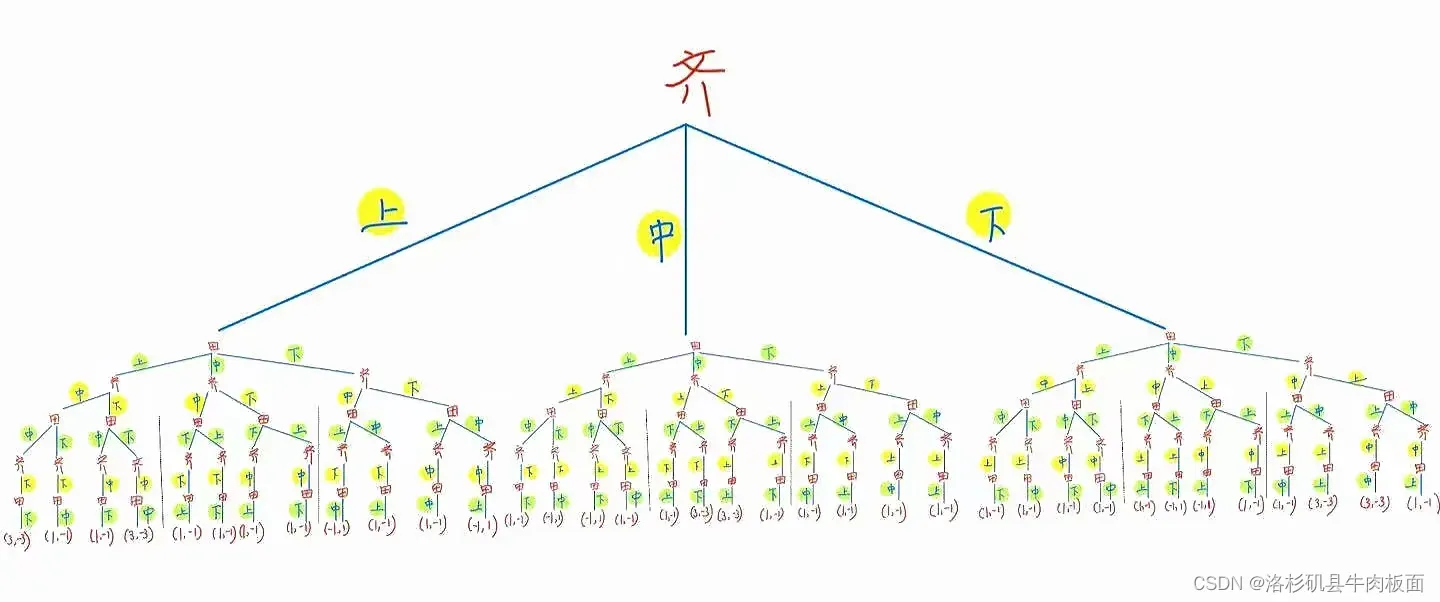

题号：34   分值：15分

34.两个朋友在一起划拳喝酒，每个人有4个纯策略：杠子、老虎、鸡和虫子。 输赢规则是：杠子降老虎，老虎降鸡，鸡降虫子，虫子降杠子。两个人同时出令，如果一方打败另一方，赢者的得益为1，输者的得益为-1，否则得益为0. 请给出以上博弈的策略式描述并求出所有的纳什均衡。

如同石头剪刀布博弈一样，此博弈不存在纯策略纳什均衡，因为这4个纯策略都互相克制。存在混合策略纳什均衡。

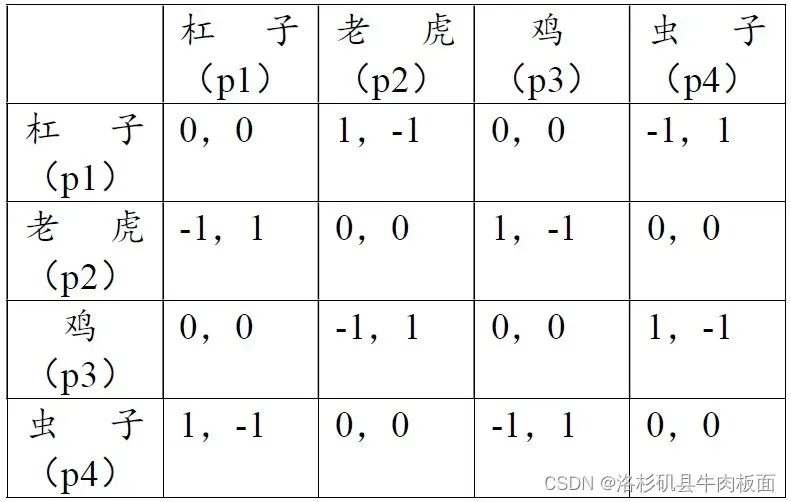
设A=杠子，B=老虎 C=鸡 D=虫子

运用“让对手猜不透原则”

设玩家1选择出A,B,C,D的概率分别为q1,q2,q3,1-q1-q2-q3  

设玩家2选择出A,B,C,D的概率分别为p1,p2,p3,1-p1-p2-p3   

对于玩家1：

对于玩家2：

得到：

  即： 

设，又因，可得混合策略:

所以，只要，就都是符合要求的纳什均衡。

如，当时，混合策略纳什均衡为。

题号：42  分值：15分

42.乙向甲索要1000元，并且威胁甲如果不给就与他同归于尽。当然，甲不一定会相信乙的威胁。 请用扩展式表示该博弈，并找出其子博弈完美纳什均衡。

这是一个完全但不完美博弈，甲并不清楚乙会不会选择威胁，故需要引入“自然”，使得乙威胁或不威胁的概率分别为50％.

设甲原本的得益为1000，乙原本的得益为0。前件为乙的得益，后件为甲的得益。

必要信息描述：

若甲不给乙，且乙的威胁是真的，甲、乙都将损失1000(因为乙不但没有得到钱，还使用了威胁的手段，损害了甲)。此时双方得益为(-1000,-1000)。

若甲给乙，乙的威胁是真的。乙提前做好了威胁甲的准备，付出了用于威胁甲的成本，成本为-200元。此时双方得益为(800，0)。

扩展式博弈(博弈树)如下：

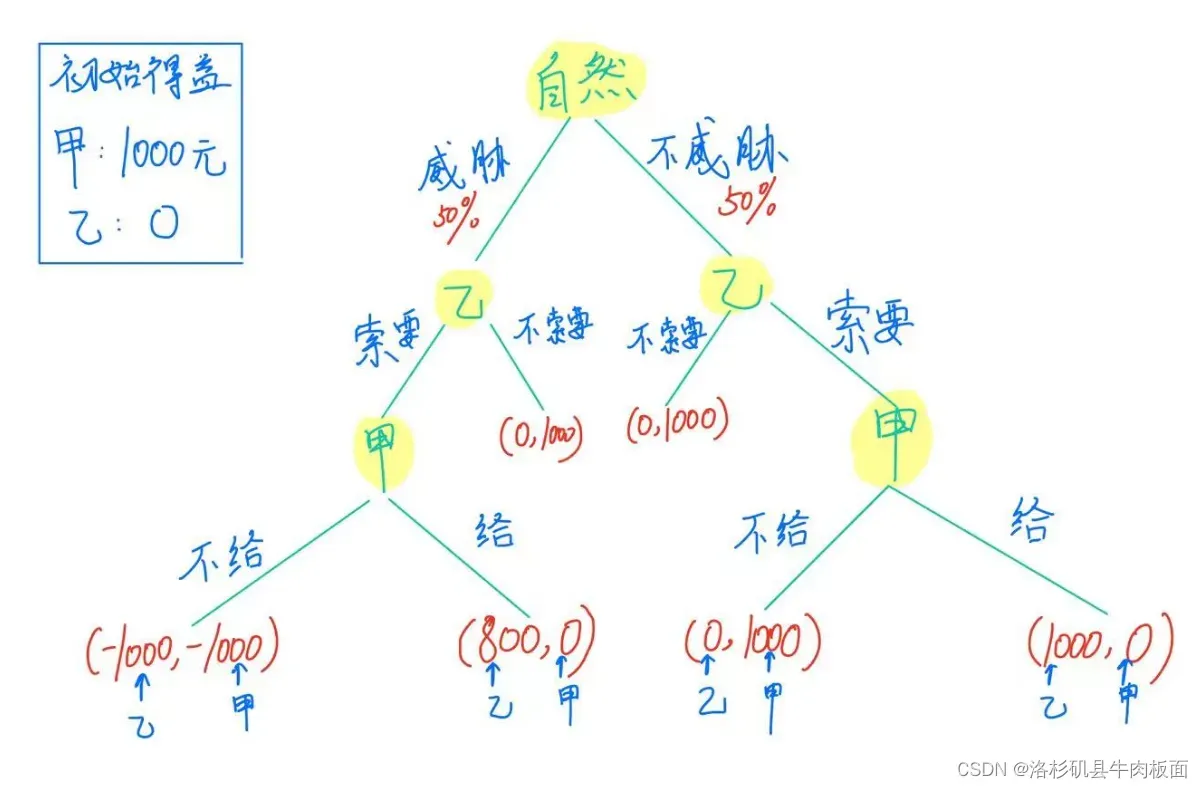
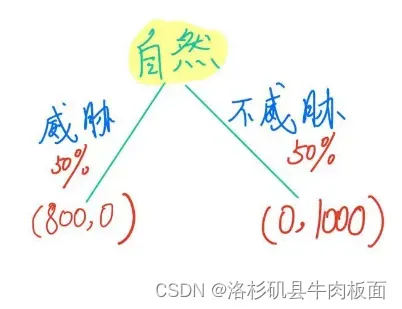
由逆向归纳法可以得到子博弈完美纳什均衡解：乙在威胁的情况下，甲选择给钱，此时双方的得益为(800,0);乙在不威胁的情况下，甲不给钱，此时双方得益为(0,1000)。

最终图解：

本博客所借鉴的优秀内容链接如下，在此鸣谢：

博弈论笔记(一)：策略式博弈及其纳什均衡 – 知乎 (zhihu.com)

博弈 习题-田忌赛马问题_田忌赛马博弈矩阵-CSDN博客