线性代数——（期末突击）行列式（上）-行列式计算、行列式的性质

行列式

行列式计算

行列式： $A_{ij}$ （i是行标，j是列标）
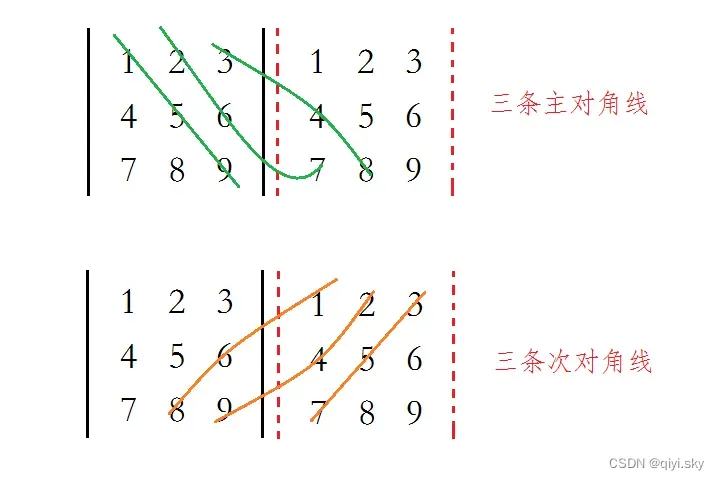
计算方法（以二阶行列式为例）：主对角线（ad）减去次对角线（bc）

$\begin{vmatrix} a &b \\ c &d \end{vmatrix}=ad-bc$

三阶行列式同理

$\begin{vmatrix} 1 &2 &3 \\ 4 &5 &6 \\ 7 &8 &9 \end{vmatrix}$

$\left [(1\times 5\times9)+(2\times6\times7)+(3\times4\times8) \right ]\: \: \: -\left [ (3\times5\times7)+(2\times4\times9)+(1\times6\times8) \right ]$

逆序数

逆序数：本质就是数一下大的数排在小的数前面的个数

例如，4213的逆序数为3+1=4。简单解释一下：4213原本的顺序应为1234，对于‘4’而言，‘2’、‘1’、‘3’都应该排在它的前面，所以此处记逆序数为3；对于‘2’而言，‘1’应该排在它的前面，而‘3’排在它之后是合理的，所以此处只有一个逆序数；最后看‘1’，其后面的‘3’排在后面显然也是合理的，故而4213的逆序数为4.

换个例子，大家可以自行理一遍：5712的逆序数为4.

行列式的性质

转置

即行列互换。

$D=\begin{vmatrix} 1 &2 &3 \\ 1& 1 &1 \\ 8&8 &8 \end{vmatrix}$ $D^T=\begin{vmatrix} 1 &1 &8 \\ 2& 1& 8\\ 3&1 &8 \end{vmatrix}$

两者的值相等。 $D=D^T$

两行（列）互换

行列式两行（列）进行互换时，其值要变号。（变换一次就变一次号）

例：

$D=\begin{vmatrix} 1 &2 &3 &4 \\ 5&6 &7 &8 \\ 9&10 &11 &12 \\ 13& 14& 15 &16 \end{vmatrix}$

将第一行和第三行互换，

$D_1=\begin{vmatrix} 9 &10 &11 &12 \\ 5& 6 & 7 &8 \\ 1&2 &3 &4 \\ 13& 14& 15&16 \end{vmatrix}$

此时 $D_1=-D$ .

两行（列）对应相等

行列式如果两行或者两列对应相等，则该行列式值为0.

$D=\begin{vmatrix} 2 &3 &4 &5 \\ 1& 0 & 0 &0 \\ 2&3 &4 & 5\\ 8& 8 &8 &1 \end{vmatrix}$ $D_1=\begin{vmatrix} 2 &3 &4 &5 \\ 1& 0 & 0 &0 \\ 2&3 &4 & 5\\ 8& 8 &8 &1 \end{vmatrix}=-D\Rightarrow D=0$

提公因子

行列式中某一行或者某一列都有公因子K，则K可以提到行列式外。（每一行提一次或者每一列提一次）

例：

$D=\begin{vmatrix} 1K &2K &3K \\ 4K& 5K& 6K\\ 7K& 8K &9K \end{vmatrix}=K^3\begin{vmatrix} 1 &2 &3 \\ 4& 5 &6 \\ 7& 8 & 9 \end{vmatrix}$

两行（列）对应成比例

若行列式两行或两列元素对应成比例，则该行列式等于0.

例：

$D=\begin{vmatrix} 1 &2 &3 \\ 1& 1 &1 \\ 8& 8 &8 \end{vmatrix}=8\begin{vmatrix} 1 &2 &3 \\ 1& 1& 1\\ 1& 1 &1 \end{vmatrix}=0$

某行（列）为零

若行列式某一行（列）为0，则该行列式=0.

注意，由D=0不能推出以下性质：

全为0
两行相等
成比例

行列式分裂

将和的那一行分开，其余行保持不变，列同理，（举例说明比较容易理解）

例：

$\begin{vmatrix} 1 &2 &3 \\ 7+8 & 2+3 &9+10 \\ 8 &8 &9 \end{vmatrix}=\begin{vmatrix} 1 &2 &3 \\ 7 & 2&9 \\ 8 &8 & 9 \end{vmatrix}+\begin{vmatrix} 1 &2 &3 \\ 8 & 3 &10 \\ 8 & 8 & 9 \end{vmatrix}$

行列式变换及三角行列式

某一行（列）乘以一个数，再加到另一行上去，其值不变。

这一性质是最重点的，也是最常用的，就不再赘述；下面回顾一下上三角行列式、下三角行列式以及反三角行列式的计算：

以主对角线为分界线的就为正三角，反之则为反三角行列式。

上三角：

$\begin{vmatrix} 1 &2 &3 \\ 0&5 &6 \\ 0& 0 &9 \end{vmatrix}=1\times5\times9=45$

下三角：

$\begin{vmatrix} 1 &0 &0 \\ 4&5 &0 \\ 7& 8&9 \end{vmatrix}=1\times5\times9=45$

反上三角：

$\begin{vmatrix} 1 &2 & 3\\ 4 & 5 &0 \\ 7 & 0 &0 \end{vmatrix}=(-1)^{\frac{n(n-1)}{2}}\times3\times5\times7=(-1)^{\frac{3(3-1)}{2}}\times105=-105$

反下三角：

$\begin{vmatrix} 0 &0 &3 \\ 0 &5 &6 \\ 7& 8 & 9 \end{vmatrix}=(-1)^{\frac{n(n-1)}{2}}\times3\times5\times7=(-1)^{\frac{3(3-1)}{2}}\times105=-105$

显然地，

$\begin{vmatrix} 1 &0 &0 \\ 0 &2 &0 \\ 0&0 & 3 \end{vmatrix}=1\times2\times3=6$

一般我们使用这个性质来计算四阶行列式，也就是将其变换成三角行列式，再计算对角线的值；称为“化三角法”。

注意：

变换过程中，先处理第一行（列），再处理第二行（列），依次向后
若第一行（列）处理完，则第一行（列）不再参与运算，往后同理

END

学习自：https://www.bilibili.com/video/BV1xM41147Mj?vd_source=11f3dfb26d11a6a6832ed5c079654e1c

原文链接：https://blog.csdn.net/li13437542099/article/details/135176632