线性矩阵不等式（LMI）（一）：简单介绍

主要从以下三个方面介绍：

什么是线性矩阵不等式(LMI)

为什么要用线性矩阵不等式(LMI)

线性矩阵不等式的发展（控制系统中）

文章目录

- 线性矩阵不等式（LMI）（一）：简单介绍

1. 线性矩阵不等式

如名字所示线性矩阵不等式三要素为：

线性 – 注意双线性时，LMI不好求解(非凸问题)；例：在不等式中出现形式，其中都为未知变量；可以利用消元法/换元法[1]转化为LMI形式；
矩阵变量 – 可以表示成一般形式/标准形式；
不等号 – 表示矩阵的正定/负定，而不是大小关系；

1.1 一般形式

LMI的一般形式可以表示为[2]：

其中，是矩阵变量，是任意矩阵，是对称矩阵。

式中，保证了的线性和对称性；通过选择合适的矩阵使得是负定的。
- 当时，LMI一般形式可以转化为Lyapunov LMI：
  
  对于控制系统来说，当存在一个正定矩阵，使得上式成立时，则系统时稳定的。
  
  Lyapunov LMI的最初解法为，通过选择调整正定矩阵，求解Lyapunov方程来求解矩阵;

1.2 标准形式

LMI的标准形式为[2]:

其中，是未知标量，称为决策变量。是已知对称矩阵。

选择标量使得上式成立；
- 例：让,
  
  其中，
  
  带入可得
  
  等价于
  
  根据上式可得取值范围为，下图所示公共部分。

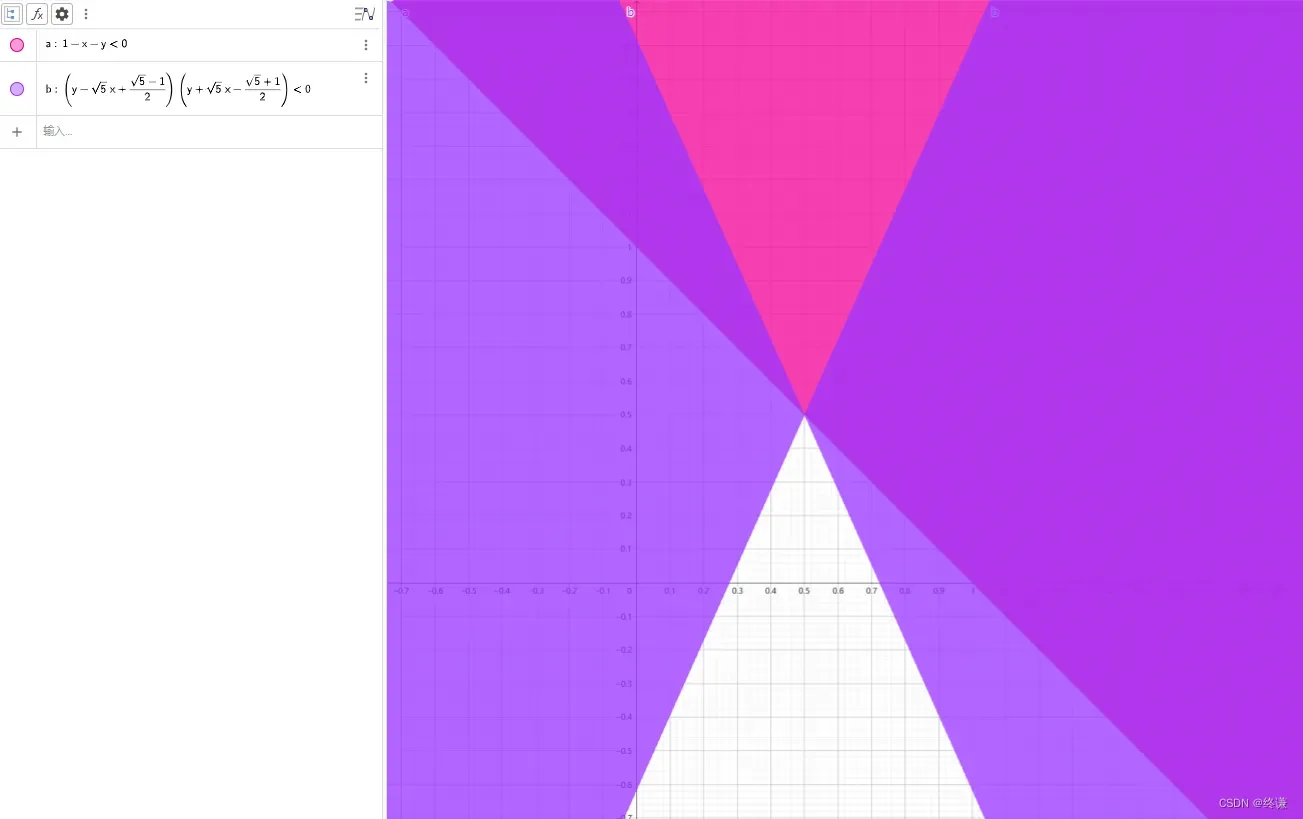
1.3 二者关系

让标准形式中为一般形式中的基底，则可表示为。定义带入到标准形式中，则可将一般形式转化为标准形式
- 例：根据Lyapunov稳定理论，二维线性系统
  
  稳定的充要条件是，存在满足不等式
  
  的正定阵。这里，2 × 2的对称阵有以下对称基底
  
  通过利用这些对称基底，**可写为
  
  将其带入(6)可得

2. 线性矩阵不等式的优点

在分析与设计控制系统中的优点[2]

全局优化解及数值可靠性

LMIs 的形式是一种凸约束形式，因此有全局最优解

可以得到可靠和有效的数值解

规模很大也可以求解

能够进行系统的多目标设计

通过将系统不同性能要求，转化为LMI组形式，共同求解LMIs，实现系统多目标设计

成熟的工具包可以使用

MATLAB LMI toolbox；（后面介绍这个）

YALMIP;（可以参考文献[3]）

CVX;（没用过不太清楚）

数值可靠性重要性！

数值可靠性可分为

good-conditioned problems （e.g. 奇异值分解），无论怎么分解都可以保证数值的精度。

ill-conditioned problems （e.g. 矩阵求逆），矩阵求逆，如果条件数很大，求的矩阵的逆精度会受到损失。

例:给定以下单输入基准系统

其中

配置系统极点

使用matlab place 命令得到的结果为：

从上可以看出place算法在一些时候并不能保证数值稳定性

2.1 LMI 是一个凸集

凸优化问题 = 凸指标+凸约束

其中是一组凸函数,等式约束必须是仿射结构(线性的)。

目标函数，是凸函数；不等式约束是凸集；等式约束时仿射的；则称此优化问题为凸优化问题。
凸函数

其中，,是一个凸集。

简单描述，函数图像上任取两点连线的中点，大于此函数任取两点对应的自变量的中点的函数值，则此函数为凸函数。
凸集

如果，且

则称是一个凸集。

简单描述，集合中任取两点连成的线段，若线段上所有的点都包含的集合里面则集合是凸集。
含有LMI的优化问题

是LMI，且是一个凸集。
- 当目标函数是凸函数时，此优化问题是凸优化问题；
  - 是一个凸集（利用凸集定义可证明）。
涉及LMI的三个标准问题

大多数问题都可以转化为标准问题
- 可行性问题
  
  找到一个解满足如下LMI:
  
  当把移动到不等式左边，令,可以将上述LMI转化为标准LMI：;
  
  上述问题可以利用，MATLAB LMI Toolbox中 feasp 命令求解。
  
  feasp 求解的时以下的带有LMI的辅助凸优化问题
  
  根据矩阵特征值特性；上式表示为使得矩阵的特征值全小于，即矩阵为负定。因此，只有凸优化问题（22）时，存在严格可行解,使得矩阵，使得成立。
- 凸最小化问题
  
  给一个凸函数，找到一个解满足以下带有LMI约束的最小化问题
  
  MATLAB LMI Toolbox中 mincx 命令求解
- 广义特征值问题
  
  找到以下最小化问题的解
  
  MATLAB LMI Toolbox中 gevp 命令求解
mincx 和 gevp 区别？凸最小化问题和广义特征值问题区别？

3. 线性矩阵不等式的发展

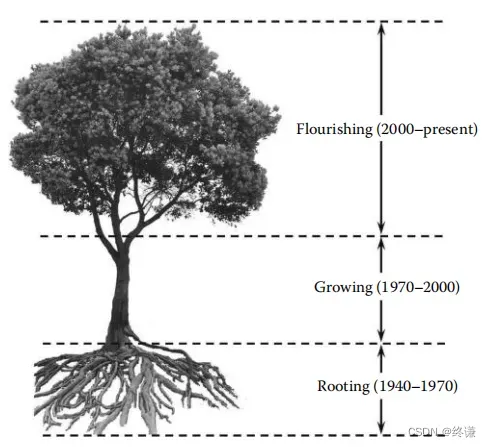
播种期(1890)

根源：求解一个正定矩阵使得成立，保证线性系统是渐进稳定的；

解决方法：Lyapunov通过选择一个正定矩阵，通过求解Lyapunov方程,来显示求解矩阵。
生根期(1940-1970)

将李亚普诺夫LMI问题应用在实际的应用中；

提出了应用图形方法求解LMI；
成长期(1970-2000)

正实引理 —— 将很多问题转化为LMI形式

凸优化算法应用 —— 为LMI求解提供了成熟的求解工具
繁荣期(2000-现在)

在鲁棒控制等领域应用很广；

参考文献

[1] Duan, G.-R., & Yu, H.-H. (2013). LMIs in Control Systems: Analysis, Design and Applications (1st ed.). CRC Press. https://doi.org/10.1201/b15060, PDF：library.lol/main/1D9AAC1BED0618920BBED953215695E2 学习视频：https://www.bilibili.com/video/BV1jt411U7xj?p=1

[2] K.-Z. Liu and Y. Yao, Robust Control: Theory and Applications. Hoboken, NJ, USA: Wiley, 2016.

[3] 刘金琨. 基于 LMI 的控制系统设计, 分析及 MATLAB 仿真[M]. 清华大学出版社, 2020.

1BED0618920BBED953215695E2](http://library.lol/main/1D9AAC1BED0618920BBED953215695E2) 学习视频：https://www.bilibili.com/video/BV1jt411U7xj?p=1

[2] K.-Z. Liu and Y. Yao, Robust Control: Theory and Applications. Hoboken, NJ, USA: Wiley, 2016.

[3] 刘金琨. 基于 LMI 的控制系统设计, 分析及 MATLAB 仿真[M]. 清华大学出版社, 2020.

原文链接：https://blog.csdn.net/weixin_42348938/article/details/135636999

线性矩阵不等式（LMI）（一）：简单介绍