目录
前言——距离判别不适合的一个例子
研究的指标是英语六级考试成绩(满分710分)。
(校研究生组):
(校本科生组):
研究生中的有1000人,本科生组中
的有2000人。某学生
该例如采用距离判别法则显然不妥,应考虑利用如下的先验概率:
距离判别方法简单,结论明确,是很实用的方法,但该方法也有缺点:
- 该判别与各总体出现的机会大小(先验概率)完全无关
- 判别方法没有考虑错判造成的损失,这是不合理的
判别正是为解决这两方面问题而提出的判别方法。
的统计思想总是假定对所研究的对象已有一定的认识,常用先验概率分布来描述这种认识。然后我们抽取一个样本,用样本修正已有的认识(先验概率分布),得到后验概率分布。
各种统计推断都通过后验概率分布来进行,将贝叶斯思想用于判别分析就得到贝叶斯判别法。
一、最大后验概率法
1.含义
设有个组
,且组
的概率密度为
,样品
来自组
的先验概率为
,满足
。则
属于
的后验概率为
最大后验概率法是采用如下的判别规则:
 2.【例5.3.1】
2.【例5.3.1】

3.先验概率的赋值方法
- 利用历史资料及经验进行估计,例如某地区成年人中得癌症的概率为
,不患癌的概率为
- 利用训练样本中各类样品所占的比例,即
,这时要求训练样本是随机抽样取得的,各类样品被抽到的机会大小就是先验概率
- 没有任何先验信息时,取等概率
4.皆为正态组的情形
设,这时组
的概率密度为
此时,后验概率为:
称为
到
的广义平方马氏距离,在正态性假定下,上述判别规则也可以等价地表达为:
(1)先验概率相等,协方差矩阵相等时
当时,
(2)仅先验概率相等时
当时,
(3)仅协方差矩阵相等时
当时,
此时,判别规则等价于:
如果我们对来自哪一组的先验信息一无所知,则一般可取
,这时判别规则简化为(距离判别):
实际应用中,以上各式中的一般都是未知的,需要相应的样本估计值代替。
5.【例5.3.2】

二、最小期望误判代价法
1.例子
:合格的药;
:不合格的药。
对于新样品,。
该问题中,两种误判造成的损失一般是明显不同的,只是根据后验概率的大小进行判别是不太合适的。
2.两组的一般情形
(1)期望误判代价
设组和
的概率密度函数分别为
,组
和
的先验概率分别为
,
.。又设将来自
的
判为
的代价为
。代价矩阵表示为:
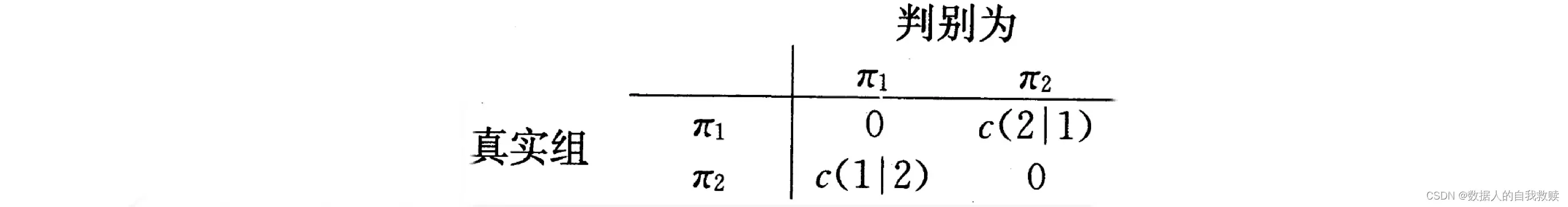
对于给定的判别规则,令={x:判别归属
} ,
={x:判别归属
},显然
判
判
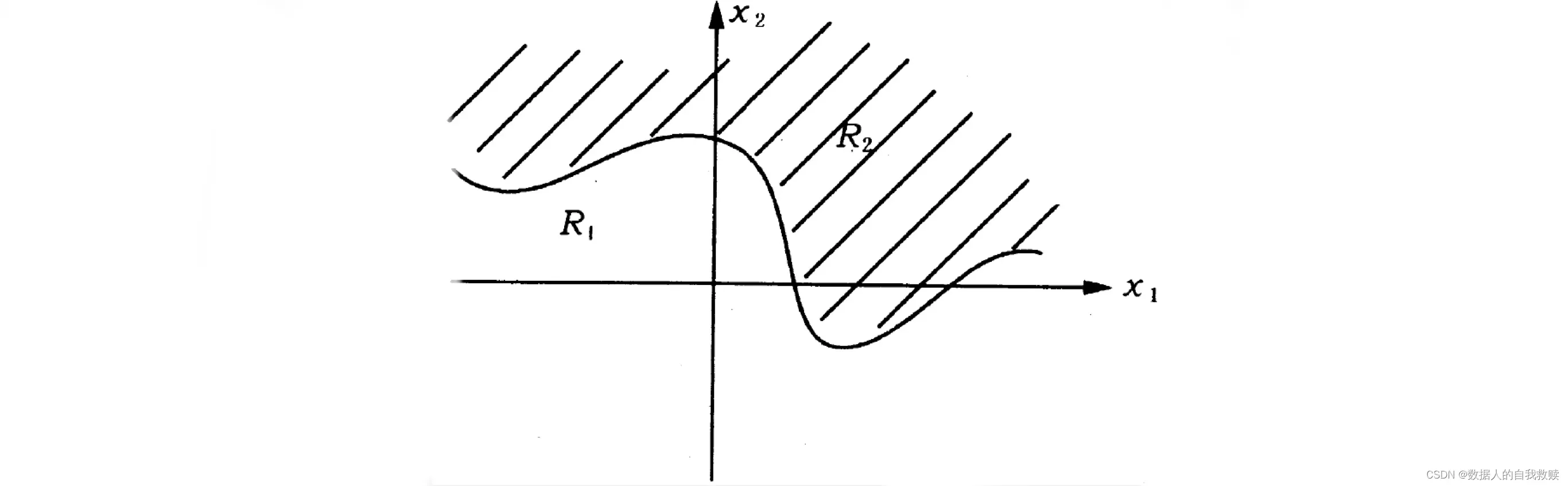 将
将中的样品
误判到
的条件概率为
类似地,将中的样品
误判到
地条件概率为
期望误判代价(
,记为
),可计算为:
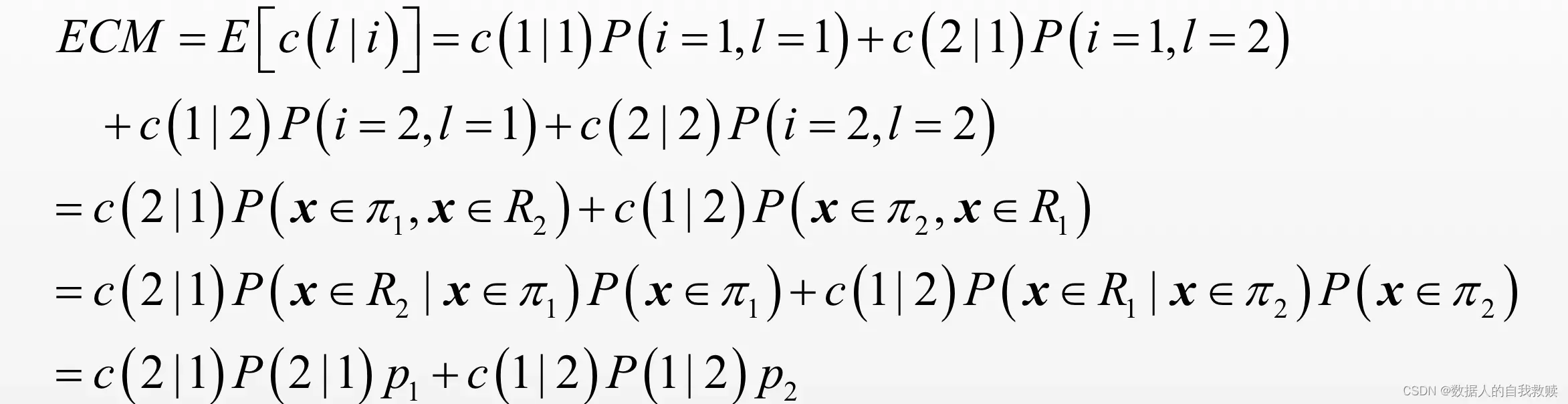 最小期望误判代价法采用的是使
最小期望误判代价法采用的是使达到最小的判别规则,即为:
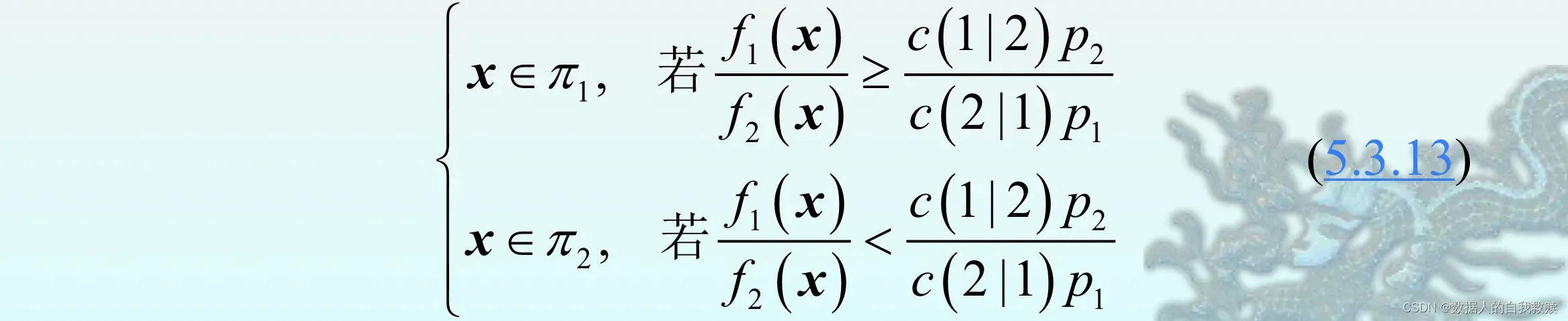
(2)误判代价之比
最小规则需要三个比值:密度函数比、误判代价比和先验概率比。在这些比值中,误判代价比最富有实际意义,因为在许多应用中,直接确定误判代价有一定困难,但是确定误判代价比却相对容易地多。
【例1】:应该做手术;
:你应该做手术
【例2】:硕士毕业后应继续攻读博士;
:硕士毕业后直接找工作
(3)【例5.3.3】

(4)(5.3.13)式的一些特殊情形
,式子简化如下。
实际应用中,如果先验概率难以给出,则它们通常被取成相等

-
时,式子简化如下。
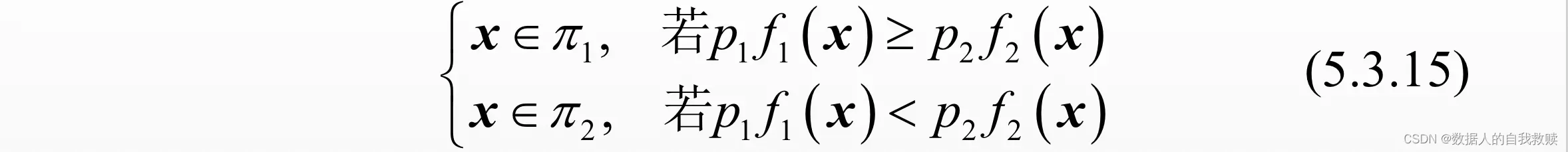
该式等价于(5.3.2)中k=2式,即为最大后验概率法。实践中,若误判代价比无法确定,则通常取比值为1。记
总的误判概率=P(误判发生在组
中)+P(误判发生在组
中)=
可见,此时的判别规则(5.3.15)将使总的误判概率()达到最小,从而此时的最小期望误判代价判别规则即为最小总误判概率判别规则。
(通常情况下是:
),式子简化如下。
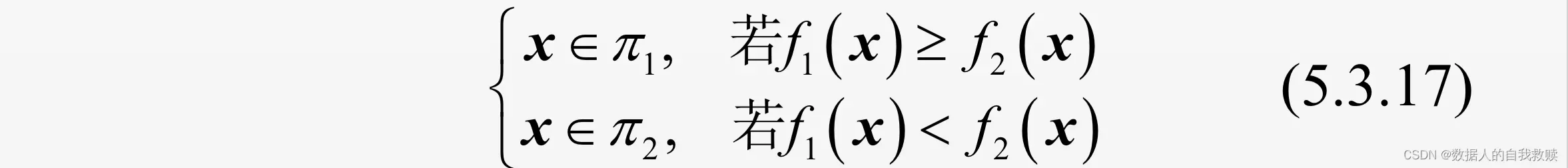
这时,判别新样品的归属,只需比较在
处的两个概率密度值
的大小。作为特例,此时他自然也使总的误判概率达到最小。 (极大似然法)
规则(5.3.17)可看成是时的判别规则(5.3.13),从而它可使
达到最小,其中
是一个不依赖于判别规则的常数,故判别规则(5.3.17)可使两个误判概率之和
达到最小,或者说可使平均误判概率
达到最小,这个平均误判概率也是当
时的总误判概率。
(5)【例5.3.4】
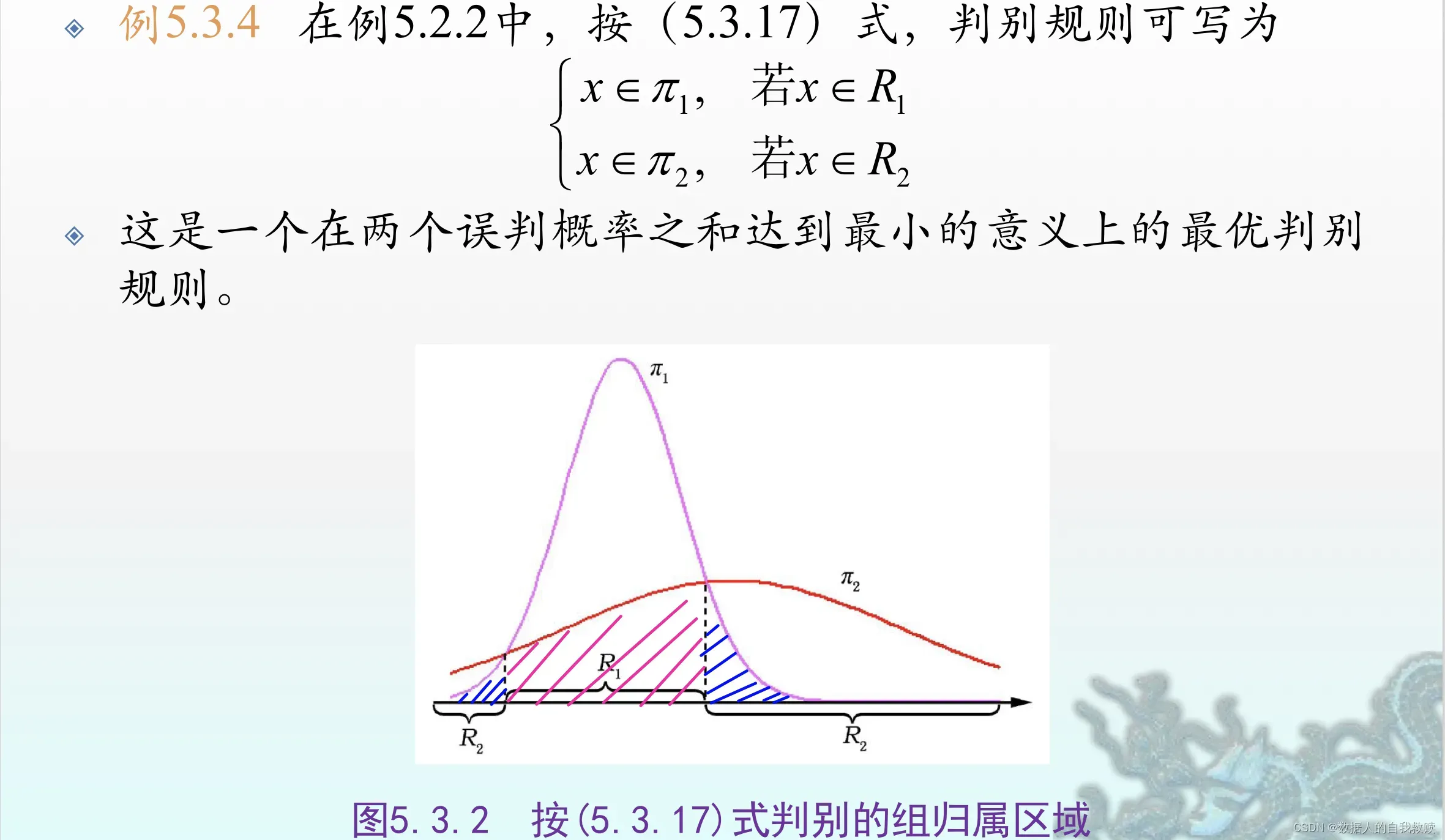
3.两个正态组的情形
假定。
(1)协方差矩阵相等时
当时,(5.3.13)式可具体写成
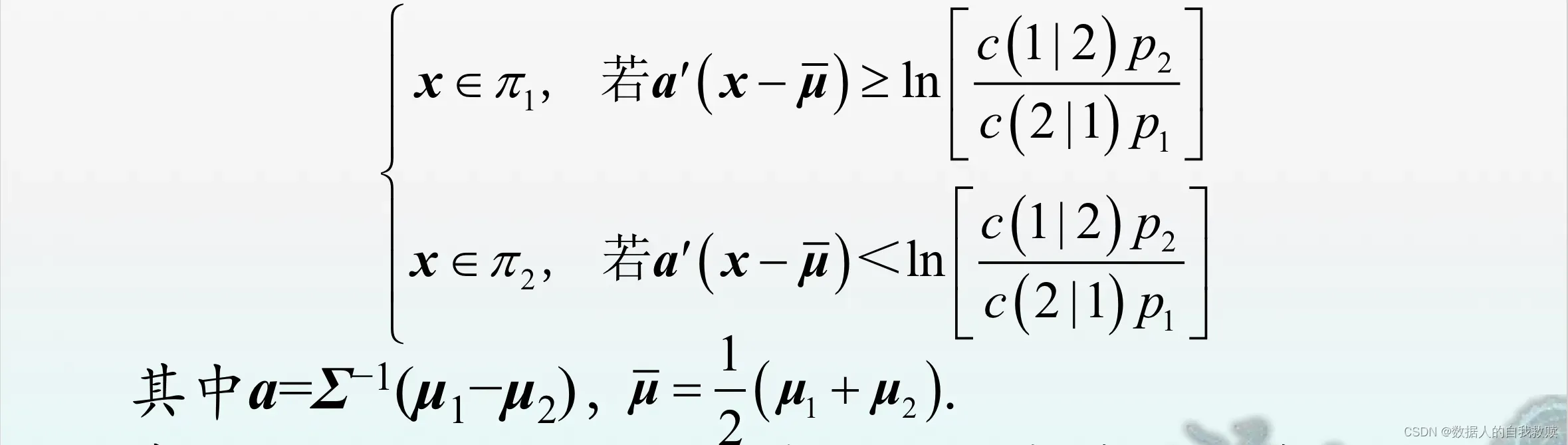
在的条件下上式将退化为(5.2.3)式。
重要结论:在两组皆为正态组且协方差矩阵相等的情形下,距离判别(5.2.3)等价于不考虑先验概率和误判代价()时的贝叶斯判别(作为(5.3.17)的一个特例),此时它是最优的,即能使总的误判概率达到最小。
实践中,因未知参数需要用样本值替代,故实际所使用的判别规则(5.2.5)只是渐进最优的。
(2)协方差矩阵不相等时
时,(5.3.13)式可写为:
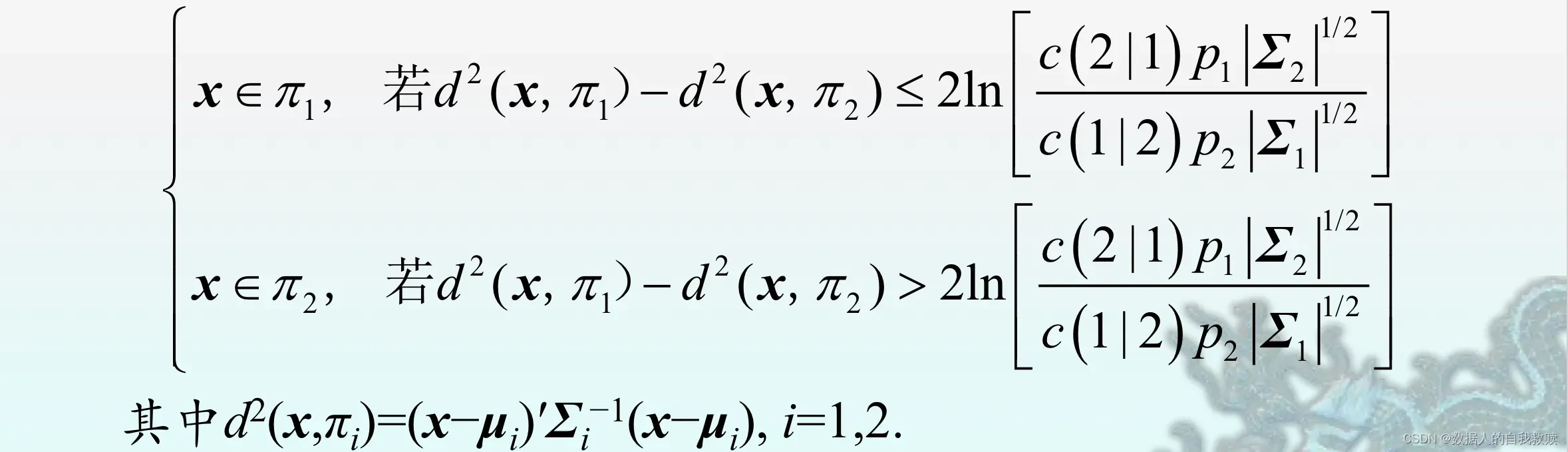
条件下上式可化简为:
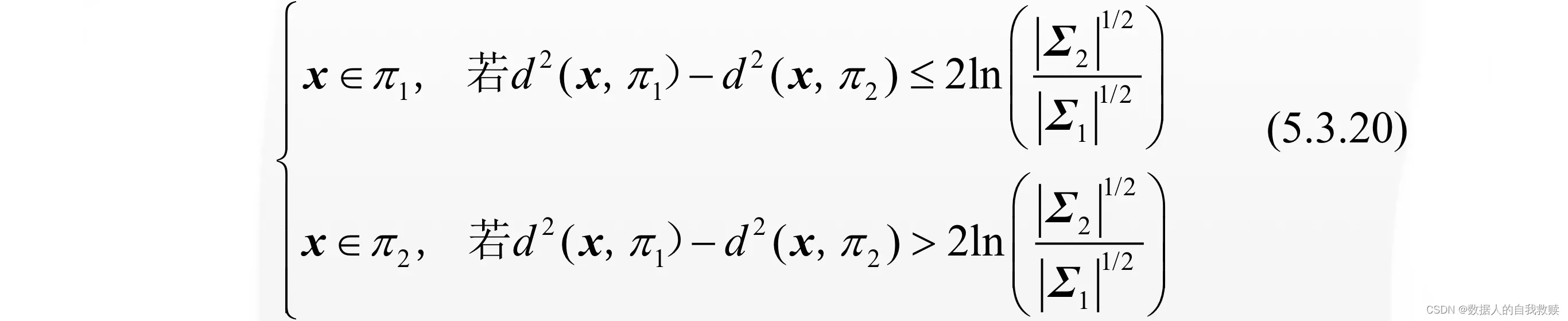
在两组均为正态组的情形下,判别规则(5.3.20)在使两个误判概率之和(或平均误判概率)达到最小的意义上是最优的。此时,它当然也就优于(5.2.10)式的距离判别。若进一步假定,则判别规则(5.3.20)将与(5.2.10)式一致。
基于二次函数的判别规则相比线性判别规则,其判别效果更依赖于多元正态性的假定。
- 实践中,为了达到较理想的判别效果,需要时可以考虑先将各组的非正态型数据变换成接近正态性的数据,然后再作判别分析。
(3)如何变换到接近正态性
计数
比例
相关系数(费希尔)
一元Box-Cox变换:。最大化
得到适当的。
多元Box-Cox变换:
(1)对每一个分量按上述一元方法进行变换:等价于使每个边缘分布接近正态,虽不能保证联合分布是正太的,但实际应用中往往可以达到足够好的效果
(2)令,求
使得
最大,其中是由
得到的样本协方差矩阵:计算更困难,不一定能够得到比方法一明显好的结果。
4.多组的情形
(1)推导
已知,
。
期望误判代价为:
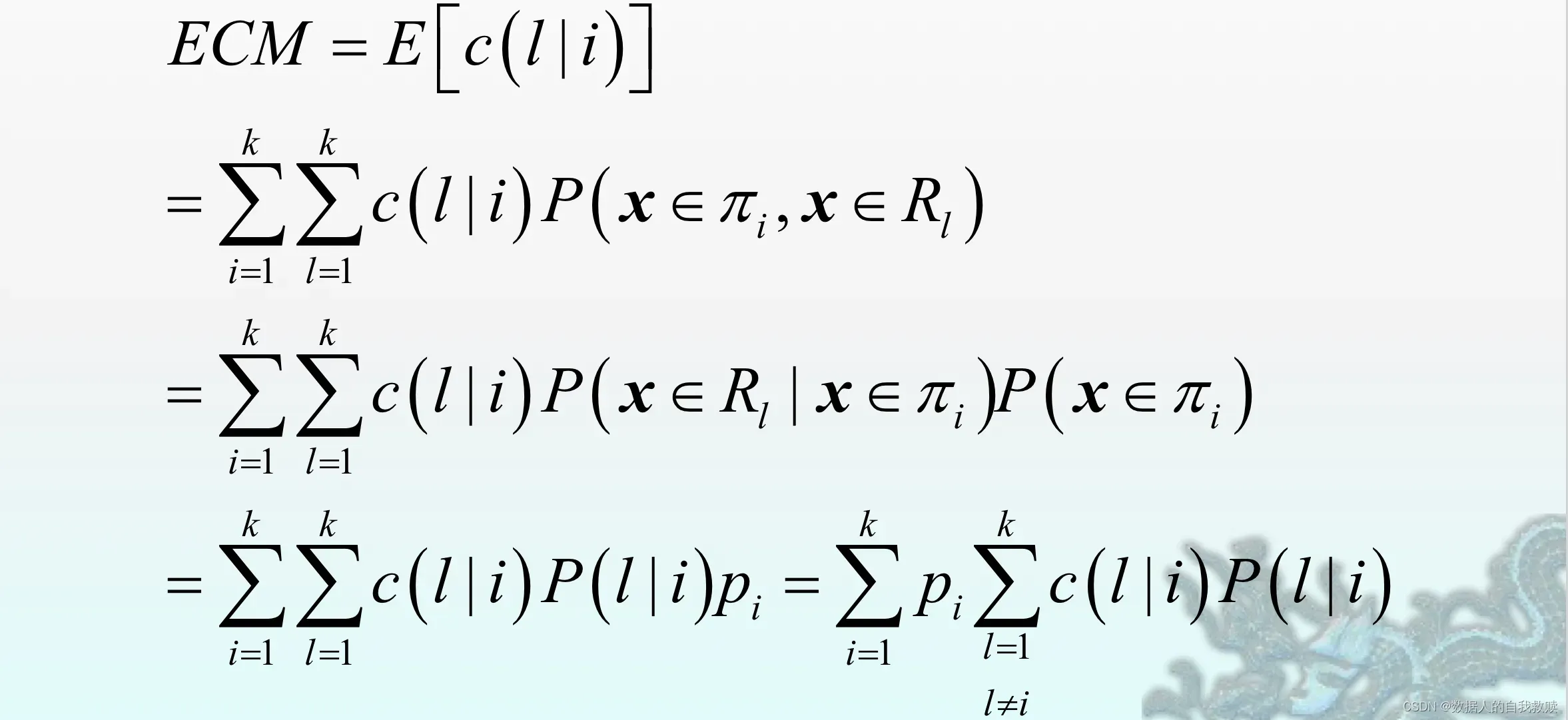
使ECM达到最小的判别规则是
假定所有的误判代价都是相同的,不失一般性,可令
则此时称为总的误判概率,故此时得最小期望误判代价也可称为最小总误判概率法,并且上式可简化为:
用减去上面等式的两边,即有更简洁的形式:
它与(5.3.2)式是等价的。因此,此时的最小误判概率法等同于最大后验概率法,或者说,最大后验概率法可看成是所有误判代价均相同的最小期望误判代价法。
当时,上式可进一步化简为:
该判别规则实际上也是一种极大似然法。
(2)【注】
令B={误判},={样品来自
},则利用全概率公式得总的误判概率为:
此外,总的正确判别概率为:
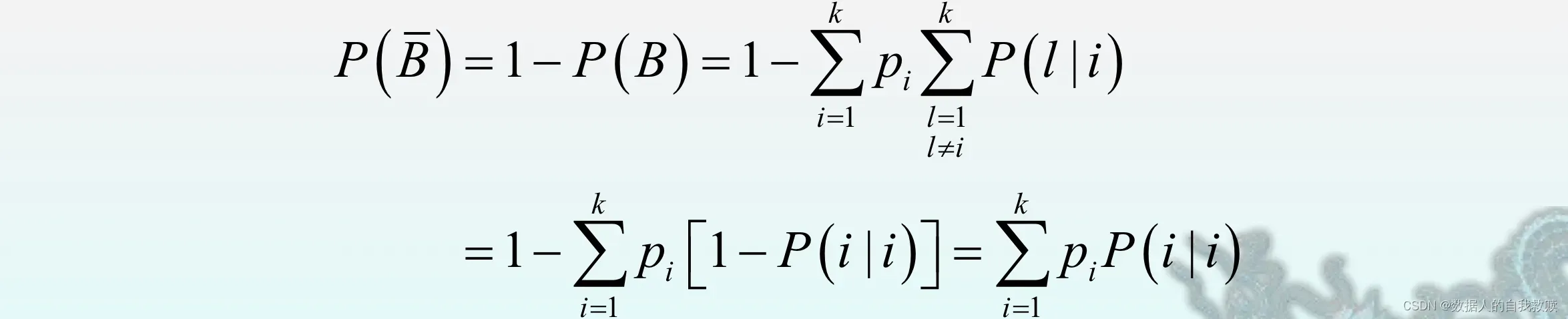 (3)【例5.3.5】
(3)【例5.3.5】

文章出处登录后可见!
