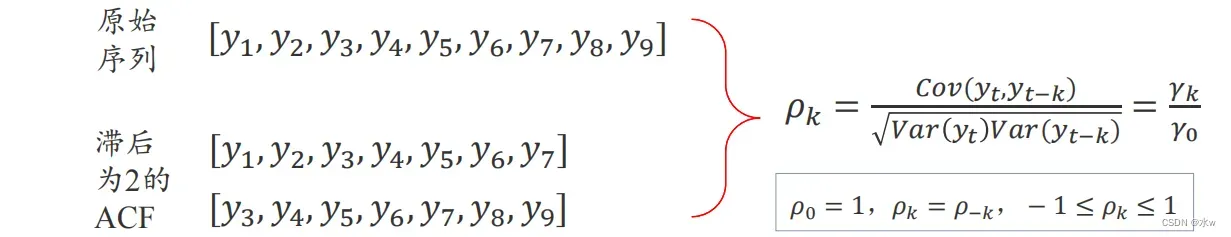目录
0、前言
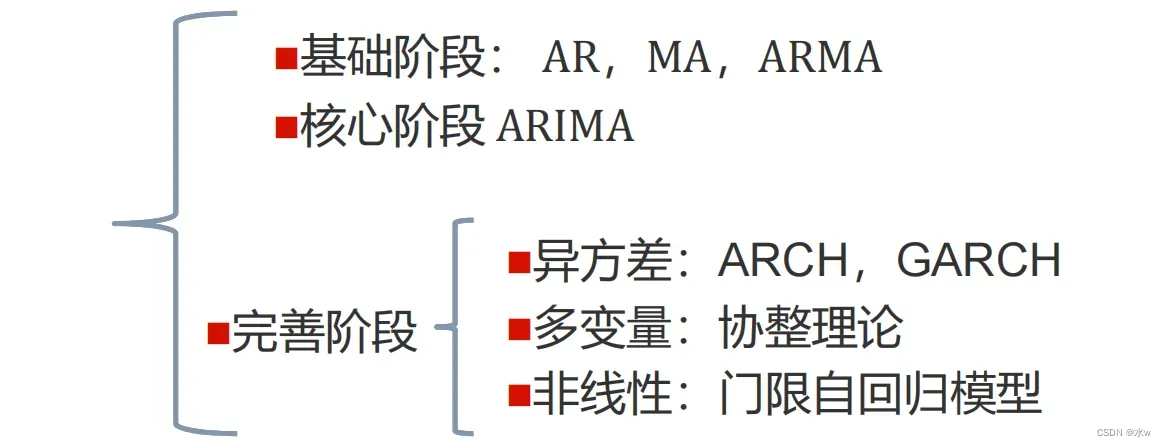
传统时间序列分析模型:
ARIMA模型是一个非常灵活的模型,对于时间序列的好多特征都能够进行描述,比如说平稳性特征,季节性特征,趋势性特征。
ARIMA模型可以通过非常成熟的统计方法,比如说极大似然估计,矩估计,贝叶斯估计或者其他一些估计方法得到估计,所以是一个非常好用的工具。
ARIMA模型分成了三部分:AR,I,MA,相当于三个模块的组合。
大家比如说,如果拿到一个时间序列,最想干什么。
如果是一个股票数据,最关心的当然是需要能够知道时刻t~t+h的收益是什么样子的,即期望,![]() 。
。
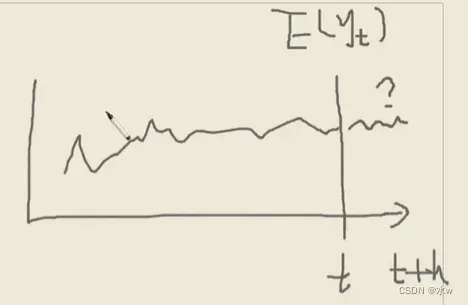
还有方差,作为一个投资者,比如预期我能赚1000万。如果方差是500,那我应该要好好考虑一下我有没有足够的把握能够控制住这个方差,赚到这个1000万。方差不确定性,就能够帮我们甄别做一件事情的风险有多大,计算公式如下:
![]()
![]()
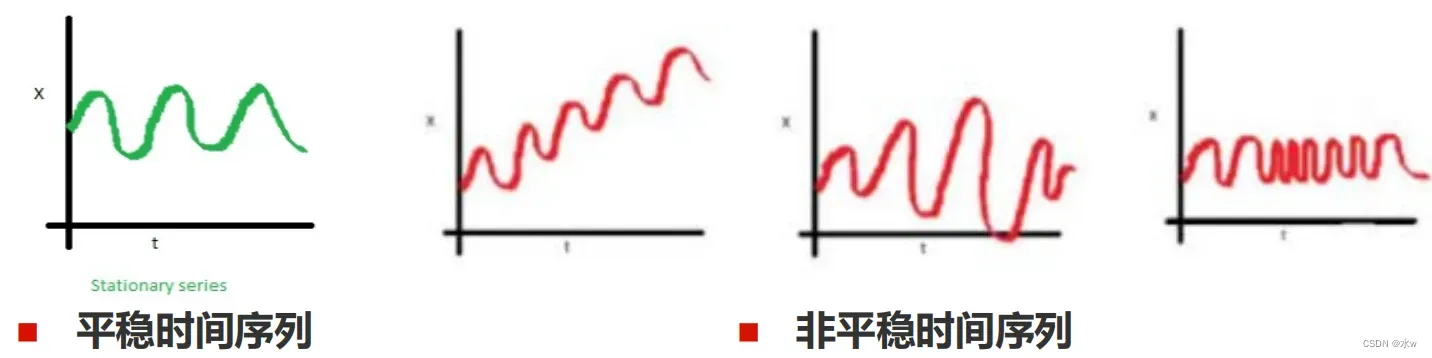
平稳时间序列:一个随机现象的统计特征不随时间变化而改变的随机过程。
非平稳时间序列:时间序列自身的随机过程的统计特征随时间改变。
一、移动平均模型MA
MA(q):假设一个时间序列由噪音(误差项)以及这些噪音的滞后阶按照不同权重组合起来。计算公式如下:

MA(q)是说,yt是和误差项以及误差项的历史阶受影响的。移动平均模型关注的是自回归模型中的误差项的累加。
二、自回归模型AR
一般的P阶自回归模型 AR:
![]()
如果随机扰动项是一个白噪声( ut=εt ),则称为一个纯AR(p)过程,记为:
![]()
自回归模型AR(p):假设今天的股票收益仅依赖于前天的股票收益,或者是依赖于前p天的股票收益,除此之外不依赖。那么前p天影响到了今天的股票收益。计算公式如下:

自回归模型首先需要确定一个阶数p,表示用几期的历史值来预测当前值。
但是,自回归模型有很多的限制:
(1)自回归模型是用自身的数据进行预测;自回归模型描述当前值与历史值之间的关系,用变量自身的历史时间数据对自身进行预测。
(2)时间序列数据必须具有平稳性;
(3)自回归只适用于预测与自身前期相关的现象(时间序列的自相关性);
三、自回归移动平均模型ARMA
可以这样理解,如果你经营一个餐馆,今天餐馆的收益和昨天的收益有关系,同时还受市场上发售的消费券的影响(假设消费券是一个随机数的话)。因为我不知道市场发了多少消费券,所以假定消费券是一个随机数。

那么你会发现,那么餐馆的经营既和过去一段时间的业绩有关系,又和消费券的随机数有关系。
那么这两个东西全部综合起来,我们把它叫做自回归移动平均模型ARMA,既有自回归模型AR,又有移动平均模型MA。计算公式如下:

ARMA本质上是一个线性模型,但是它非常灵活,它能够帮助我们描述很多不同的场景。由于它是一个递归的形式,可以通过递归的形式来预测yt-1,yt-2,yt-3,所以ARMA模型是一个非常非常有效的基准的时间序列检测工具。
四、自回归移动平均模型ARIMA
现在,我们想想这个“I”是什么东西,“I”是一个差分项。
也就是说任何一个时间序列,你拿到之后,你需要想一想它是不是平稳的。如果不是平稳的,那么我们需要进行差分,即d=1,yt-yt-1就是差分之后的形式。
![]()
这里的p是自回归模型AR的参数,q是移动平均模型MA的参数,d是指d阶差分。
因为差分后的时间序列往往有更好的平稳性,那么差分后的时间序列就可以更好的用ARMA模型来建模。
ARIMA(p,d,q):假设今天的股票收益不仅依赖于前p天的股票收益,同时还与消费券有关。
除了差分, 比如说还有Box-Jenkins方法,是一个比较主观的工具。但是它对于较长的时间序列不是很好用,然后呢还有一些检验上的问题都很难被处理。
差分:将不平稳的时间序列变平稳。
Box-Jenkins方法:通过查看acf和pcf来识别这个时间序列是不是平稳的。
样本自相关函数(autocorrelation function,ACF):展现t时刻和t-k时刻时间序列的关联性,描述的是时间序列观测值与其过去的观测值之间的线性相关性。
样本偏自相关函数(partial autocorrelation function,PACF) :在给定了
的条件下, 𝑦t与滞后 𝑘 期时间序列之间的条件相关。
PACF描述的是在给定中间观测值的条件下,时间序列观测值预期过去的观测值之间的线性相关性。
举个简单的例子,假设k=3,那么我们描述的是yt和yt-3之间的相关性,但是这个相关性还受到yt-1和yt-2的影响。PACF剔除了这个影响,而ACF包含这个影响。
【总结】

文章出处登录后可见!