1. AI技术聚合首页
  2. Python

【Python数据科学快速入门系列 | 10】Matplotlib数据分布图表应用总结

xiaoxingxing • • Python • 阅读 208

这是机器未来的第59篇文章

原文首发地址：https://robotsfutures.blog.csdn.net/article/details/127484292

【Python数据科学快速入门系列 | 10】Matplotlib数据分布图表应用总结

《Python数据科学快速入门系列》快速导航：

文章目录

写在开始：

  • 博客简介：专注AIoT领域，追逐未来时代的脉搏，记录路途中的技术成长！
  • 博主社区：AIoT机器智能, 欢迎加入！
  • 专栏简介：从0到1掌握数据科学常用库Numpy、Matploblib、Pandas。
  • 面向人群：AI初级学习者

1. 概述

本篇文章总结常用的数据分布图表。数据分布图表强调数据集中的数值及其频率或分布规律。常见的有统计直方图、核密度曲线图、箱形图、小提琴图等。

【Python数据科学快速入门系列 | 10】Matplotlib数据分布图表应用总结

2. 常用的数据分布图表应用

2.1 统计直方图

直方图(Histogram)，又称质量分布图，是一种统计报告图，由一系列高度不等的纵向条纹或线段表示数据分布的情况。 一般用横轴表示数据范围，纵轴表示分布情况。其特点是绘制连续性的数据展示一组或者多组数据的分布状况(统计)

统计直方图涉及统计学概念，首先找到数据的最大、最小值，然后确定一个区间，使其包含全部测量数据。然后将数据区间分为若干个小区间，然后统计每个区间分组内测量数据的数量。在坐标系中，横轴标出每个组的端点，纵轴表示频数，每个矩形的高代表对应的频数，称这样的统计图为频数分布直方图。

直方图的主要作用有：

  • 能够显示数据分布情况或展示各组数据的频数；
  • 易于显示各组数据之间的频数或数量的差别，通过直方图还可以观察和估计哪些数据比较集中，异常或孤立的数据分布。

与柱状图对比：
柱状图是以矩形的长度表示每一组的频数或数量，其宽度(表示类别)则是固定的，利于较小的数据集分析。
直方图是以矩形的长度表示每一组的频数或数量，宽度则表示各组的组距，因此其高度与宽度均有意义，利于展示大量数据集的统计结果。
由于分组数据具有连续性，直方图的各矩形通常是连续排列，而柱状图则是分开排列。

import numpy as np
from matplotlib import pyplot as plt

"""
    加载鸢尾花数据集
"""
import numpy as np

data = []
column_name = []
with open(file='iris.txt',mode='r') as f:
    # 过滤标题行
    line = f.readline()
    if line:
        column_name = np.array(line.strip().split(','))
        
    while True:
        line = f.readline()
        if line:
            data.append(line.strip().split(','))
        else:
            break

data = np.array(data,dtype=float)

# 使用切片提取前4列数据作为特征数据
X_data = data[:, :4]  # 或者 X_data = data[:, :-1]

# 使用切片提取最后1列数据作为标签数据
y_data = data[:, -1]

data.shape, X_data.shape, y_data.shape

((150, 5), (150, 4), (150,))

"""
展示鸢尾花不同特征的数据分布情况
"""

# windows配置SimHei，Ubuntu配置WenQuanYi Micro Hei
plt.rcParams["font.sans-serif"]=["WenQuanYi Micro Hei"] #设置字体
plt.rcParams["axes.unicode_minus"]=False #该语句解决图像中的“-”负号的乱码问题

fig, ax = plt.subplots(figsize=(12,9))
ax.hist(X_data[:, 0], bins=16, alpha = 0.7, density=True, label="花萼长度")
ax.hist(X_data[:, 1], bins=16, alpha = 0.7, density=True, label="花萼宽度")
ax.hist(X_data[:, 2], bins=16, alpha = 0.7, density=True, label="花瓣长度")
ax.hist(X_data[:, 3], bins=16, alpha = 0.7, density=True, label="花瓣宽度")
ax.legend()

plt.show()


png
​

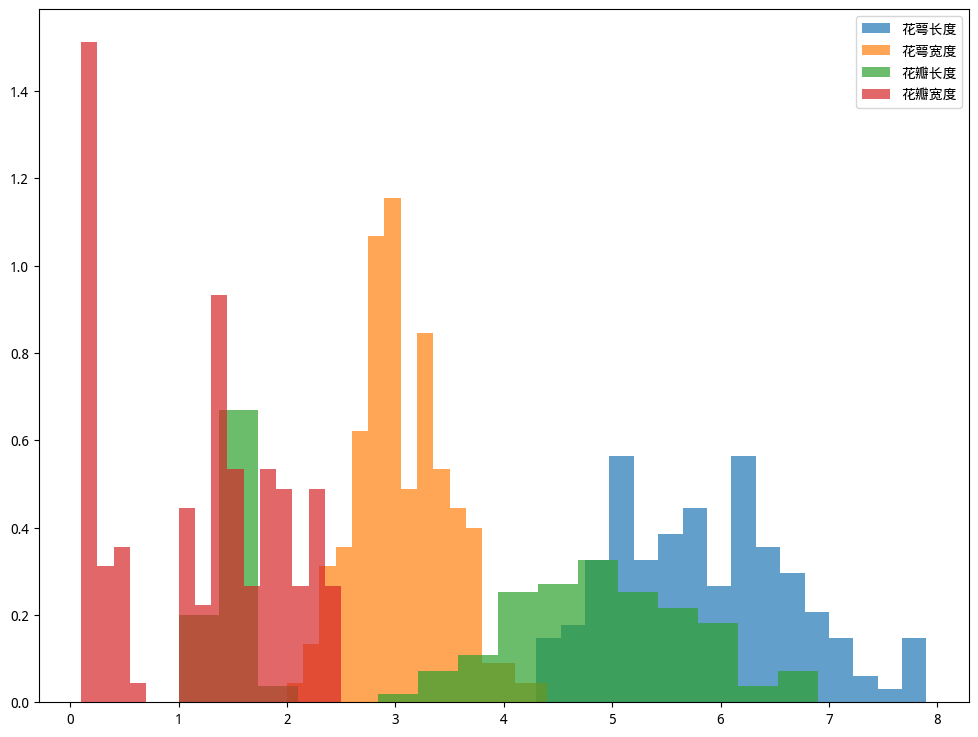
x – 数据集
bins – 分组数量，对应组距
alpha – 对应多个图例时，图例图表的透明度，可以同时展示多个图例
density – 将纵轴的频数转换为密度标识，所有的分组的的高度密度乘积之后为1
label – 图表的名称

2.2 核密度估计曲线

核密度估计图用于显示数据在X轴连续数据段内的分布状况，这种图表是直方图的变种，使用平滑曲线来绘制数值水平，从而得出更平滑的分布。其优于统计直方图的地方在于它们不受所使用分组数量的影响，所以能更好地界定分布形状。

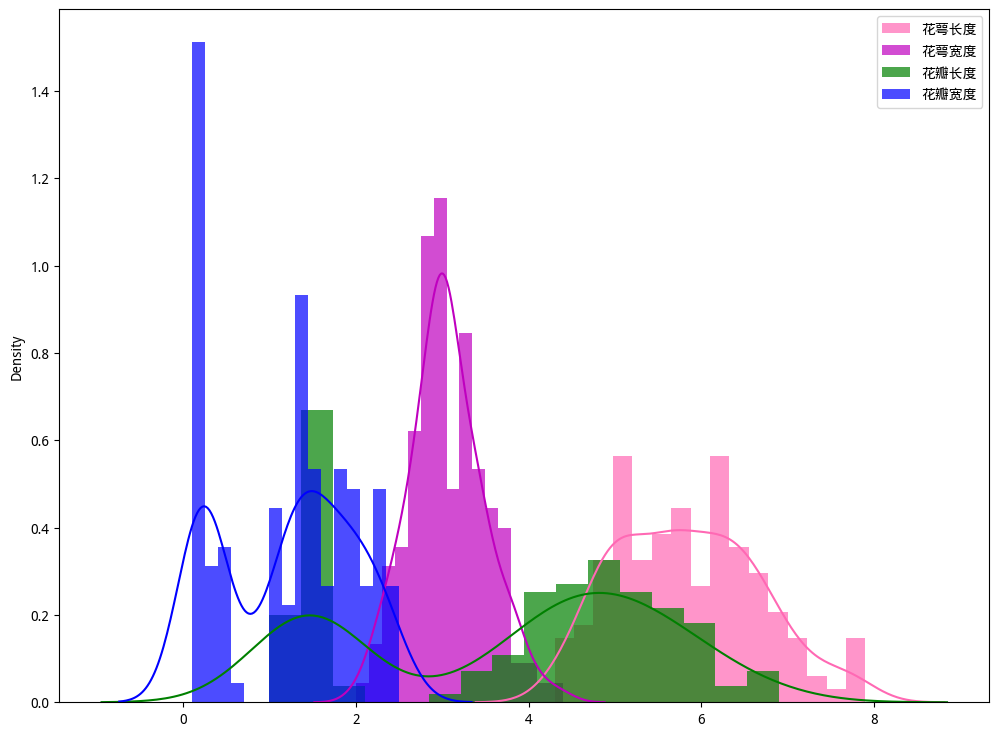
import seaborn as sns

fig, ax = plt.subplots(figsize=(12, 9))

"""
展示鸢尾花不同特征的数据分布情况
"""
plt.rcParams["font.sans-serif"]=["WenQuanYi Micro Hei"] #设置字体
plt.rcParams["axes.unicode_minus"]=False #该语句解决图像中的“-”负号的乱码问题

ax.hist(X_data[:, 0], bins=16, alpha = 0.7, density=True, color='hotpink', label="花萼长度")
ax.hist(X_data[:, 1], bins=16, alpha = 0.7, density=True, color='m', label="花萼宽度")
ax.hist(X_data[:, 2], bins=16, alpha = 0.7, density=True, color='green', label="花瓣长度")
ax.hist(X_data[:, 3], bins=16, alpha = 0.7, density=True, color='b', label="花瓣宽度")

sns.kdeplot(X_data[:, 0], ax=ax, color='hotpink')
sns.kdeplot(X_data[:, 1], ax=ax, color='m')
sns.kdeplot(X_data[:, 2], ax=ax, color='green')
sns.kdeplot(X_data[:, 3], ax=ax, color='b')

ax.legend()
plt.show()


png
​

2.3 箱形图

箱形图最大的优点就是不受异常值的影响，能够准确稳定地描绘出数据的离散分布情况，同时也利于数据的清洗。

箱型图（也称为盒须图）于 1977 年由美国著名统计学家约翰·图基（John Tukey）发明。它能显示出一组数据的最大值、最小值、中位数、及上下四分位数。

在箱型图中，我们从上四分位数到下四分位数绘制一个盒子，然后用一条垂直触须（形象地称为“盒须”）穿过盒子的中间。上垂线延伸至上边缘（最大值），下垂线延伸至下边缘（最小值）。

箱型图结构如下所示：

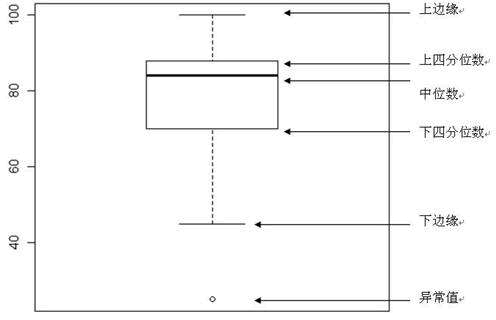
【Python数据科学快速入门系列 | 10】Matplotlib数据分布图表应用总结

在箱型图中，我们从上四分位数到下四分位数绘制一个盒子，这意味着箱子包含了50%的数据。因此，箱子的宽度在一定程度上反映了数据的波动程度。

箱线图和正态分布的关系

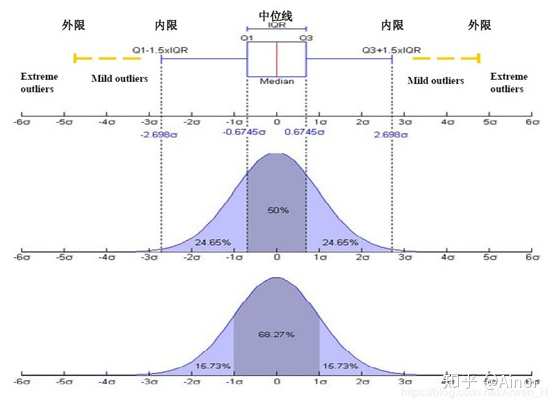
【Python数据科学快速入门系列 | 10】Matplotlib数据分布图表应用总结

箱型图的应用场景：配合着定性变量画分组箱线图，作比较。

2.3.1 实例分析

什么叫做定性，简单来说就是分类，举个简单的例子，鸢尾花数据集，以单个特征在数据集多个分类上的的数值分布、中位数、波动程度及异常值。

# 箱形图
# 进一步查看某种类下，各特征的值分布, 圆圈是离群点

print(X_data[y_data==0].shape, column_name.shape, y_data.shape)

# 山鸢尾（Setosa）、变色鸢尾（Versicolor）、维吉尼亚鸢尾（Virginical）
label_class_name = np.array(['Setosa', 'Versicolor', 'Virginical'])

fig, ax = plt.subplots(1, 4, figsize=(15, 6))

for i in range(4):
    # 添加y轴标签
    ax[i].set_ylabel(column_name[i])
    # 对标签对应的数据进行组合
    X_data_p = [X_data[y_data == 0][:, i], X_data[y_data == 1][:, i], X_data[y_data == 2][:, i]]
    # 绘制箱形图、横轴标签
    bplot = ax[i].boxplot(X_data_p, patch_artist=True, labels=label_class_name[0:3])

    ###遍历每个箱子对象
    colors = ['pink', 'lightblue', 'lightgreen']  ##定义柱子颜色、和柱子数目一致
    for patch,color in zip(bplot['boxes'],colors): ##zip快速取出两个长度相同的数组对应的索引值
        patch.set_facecolor(color)   ##每个箱子设置对应的颜色

# 调整子图上下间距
plt.subplots_adjust(left=None, bottom=None, right=None, top=None, wspace=0.3, hspace=0.0)
plt.show()

(50, 4) (5,) (150,)

png

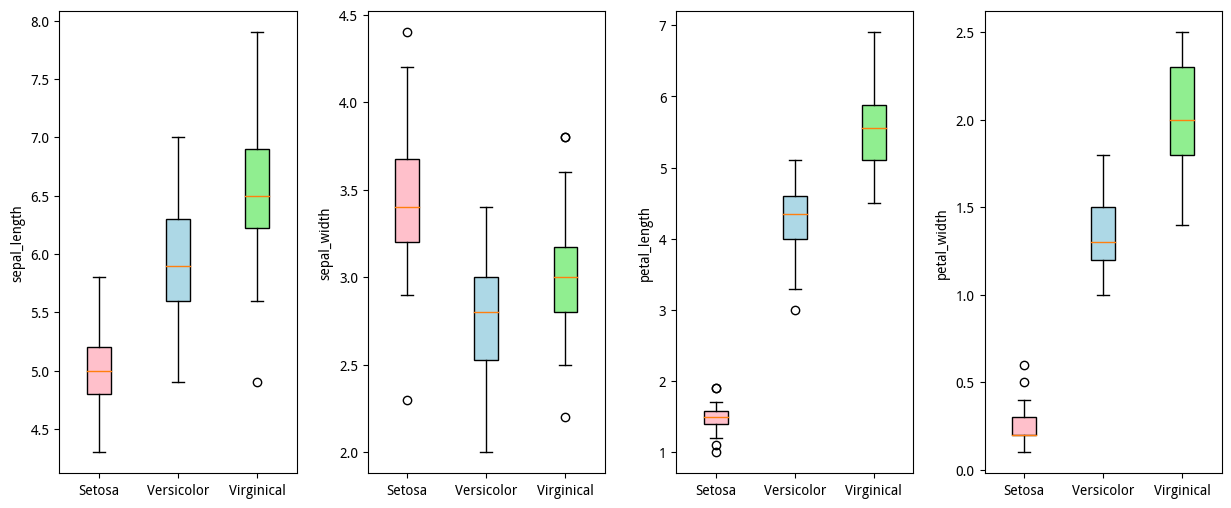
从上面的图可以看到，以鸢尾花特征做定性分组，可以看到分组时不同的标签的箱型图位置错落有致，位置区别其实还是比较明显的，箱型其实代表的中位数附近累计50%的特征数据，箱型的上下边界代表上下四分位数，从上下四分位数的上下间距可以看到很直观的不同特征的数据波动的范围，还可以看到空心圆代表的异常值。

从最左侧的第一幅图花萼长度sepal_length与鸢尾花数据标签的数据关系分布来看：

  • 花萼长度sepal_length在Setosa分类中中位数较小，Versicolor鸢尾花中位数较大，Virginical鸢尾花中位数最大；
  • 箱子的长短代表了各组数据的集中程度，花萼长度sepal_length在Setosa鸢尾花中数据相对集中，Versicolor鸢尾花和Virginical鸢尾花相对分散；
  • 中位数与箱子的位置表现了各组数据的分布状态。花萼长度sepal_length在Setosa鸢尾花中呈正态分布，花萼长度sepal_length在Versicolor鸢尾花和Virginical鸢尾花中呈右偏分布；

2.3.2 箱型图的价值

  • 直观明了地识别数据批中的异常值。
  • 利用箱线图判断数据批的偏态和尾重。

对于标准正态分布的样本，只有极少值为异常值。异常值越多说明尾部越重，自由度越小（即自由变动的量的个数）；而偏态表示偏离程序，异常值集中在较小值一侧，则分布呈左偏态，异常值集中在较大值一侧，则分布呈右偏态。

  • 利用箱型图比较几批数据的形状。

同一数轴上，几批数据的箱型图并行排列，几批数据的中位数、尾长、异常值、分布区间等形状信息便一目了然。

2.3.3 箱型图和直方图的选择

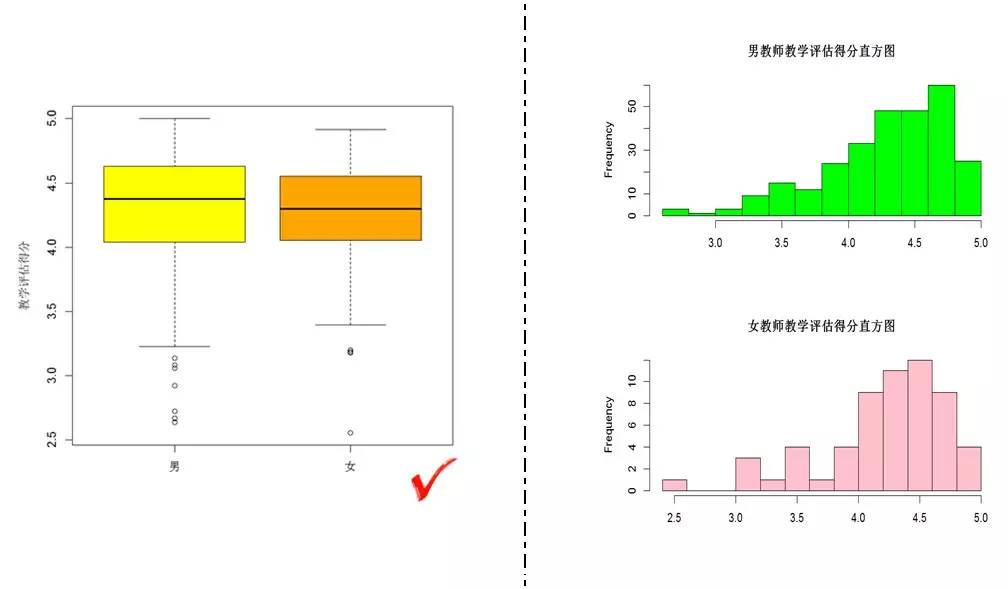
【Python数据科学快速入门系列 | 10】Matplotlib数据分布图表应用总结

假设我现在要比较男女教师的教学评估得分，用什么工具最好。答案是箱线图。没有比较就没有伤害，大家看上图够明显感觉到箱线图是更有效的工具，能够从平均水平（中位数），波动程度（箱子宽度）以及异常值对男女教师的教学评估得分进行比较，而直方图却做不到。

2.3.4 使用总结

  • 箱线图是针对连续型变量的，解读时候重点关注平均水平、波动程度和异常值。

  • 当箱子被压得很扁，或者有很多异常的时候，试着做对数变换。当只有一个连续型变量时，并不适合画箱线图，直方图是更常见的选择。

  • 箱线图最有效的使用途径是作比较，配合一个或者多个定性数据，画分组箱线图。

箱型图的局限性：

  • 不能精确地衡量数据分布的偏态和尾重程序；
  • 对于批量比较大的数据，反映的信息更加模糊以及用中位数代表总体评价水平有一定的局限性。

2.4 小提琴图

小提琴图可以理解为箱型图+核密度估计曲线图。

小提琴图（Violin Plot）是用来展示数据分布状态以及概率密度的图表。这种图表结合了箱形图和密度图的特征。小提琴图跟箱形图类似，不同之处在于小提琴图还显示数据在不同数值下的概率密度。

小提琴图使用核密度估计（KDE）来计算样本的分布情况，图中要素包括了中位数、四分位间距以及置信区间。在数据量非常大且不方便一一展示的时候，小提琴图特别适用。

# 箱形图
# 进一步查看某种类下，各特征的值分布, 圆圈是离群点

print(X_data[y_data==0].shape, column_name.shape, y_data.shape)

# 山鸢尾（Setosa）、变色鸢尾（Versicolor）、维吉尼亚鸢尾（Virginical）
label_class_name = np.array(['Setosa', 'Versicolor', 'Virginical'])

fig, ax = plt.subplots(1, 4, figsize=(15, 6))

for i in range(4):
    # 添加y轴标签
    ax[i].set_ylabel(column_name[i])
    # 对标签对应的数据进行组合
    X_data_p = [X_data[y_data == 0][:, i], X_data[y_data == 1][:, i], X_data[y_data == 2][:, i]]
    # 绘制箱形图、横轴标签
    bplot = ax[i].violinplot(X_data_p, showmedians=True)

# 调整子图上下间距
plt.subplots_adjust(left=None, bottom=None, right=None, top=None, wspace=0.3, hspace=0.0)
plt.show()

(50, 4) (5,) (150,)

png

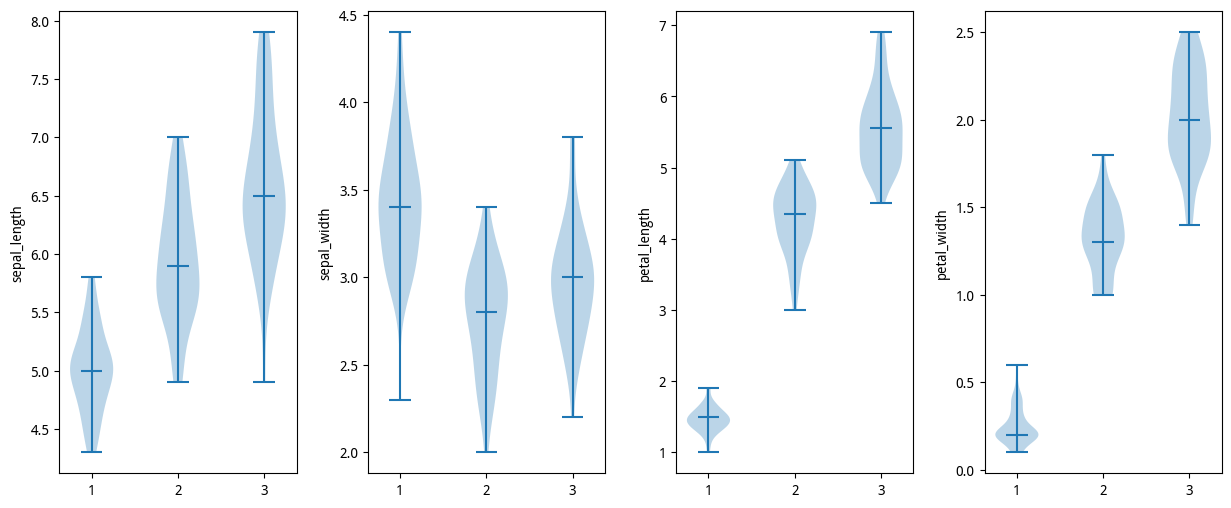
3. 总结

从上面的常用数据分布图表来看，他们都是适用于连续数据分布的应用场景。

直方图能够显示数据分布情况或展示各组数据的频数，易于显示各组数据之间的频数或数量的差别，通过直方图还可以观察和估计哪些数据比较集中，异常或孤立的数据分布。

核密度估计曲线其优于统计直方图的地方在于它们不受所使用分组数量的影响，所以能更好地界定分布形状。

箱型图能够准确稳定地描绘出数据的离散分布情况，直观明了地识别数据批中的异常值，数据波动及数据分布规律，典型应用于定性对比分析。

而小提琴图可以理解为箱型图+核密度估计曲线图的合体，除了箱型图的优点，还展示数据在不同数值下的概率密度，尤其适用于数据量大的应用场景。

参考文献：

— 博主热门专栏推荐 —

【Python数据科学快速入门系列 | 10】Matplotlib数据分布图表应用总结

文章出处登录后可见！

已经登录？立即刷新

共计人评分，平均分

到目前为止还没有投票！成为第一位评论此文章。

赞 (0)
xiaoxingxing的头像xiaoxingxing管理团队
0
上一篇 2023年3月5日 上午10:37
下一篇 2023年3月5日 上午10:38

相关推荐

此站出售，如需请站内私信或者邮箱！