超参数调试、Batch正则化和编程框架

参考链接：链接：https://blog.csdn.net/red_stone1/article/details/78403416

1. Tuning Process
深度神经网络需要调试的超参数（Hyperparameters）较多，包括：

α：学习率

β：动量梯度下降因子

β1,β2,ε：Adam算法参数

#layers：神经网络层数

#hidden units：各隐藏层神经元个数

learning rate decay：学习因子下降参数

mini-batch size：批量训练样本包含的样本个数

超参数之间也有重要性差异。通常来说，学习因子α是最重要的超参数，也是需要重点调试的超参数。动量梯度下降因子β、各隐藏层神经元个数#hidden units和mini-batch size的重要性仅次于αα。然后就是神经网络层数#layers和学习因子下降参数learning rate decay。最后，Adam算法的三个参数β1,β2,εβ1,β2,ε一般常设置为0.9，0.999和10−8，不需要反复调试。当然，这里超参数重要性的排名并不是绝对的，具体情况，具体分析。

模型调参注意细节

神经网络的调参效果不理想时->(解决思路) – 账号 – 博客园

非过拟合情况

1. 是否找到合适的损失函数？(不同问题适合不同的损失函数)(理解不同损失函数的适用场景)
   (解决思路)选择合适的损失函数（choosing proper loss ）
   神经网络的损失函数是非凸的，有多个局部最低点，目标是找到一个可用的最低点。非凸函数是凹凸不平的，但是不同的损失函数凹凸起伏的程度不同，例如下述的平方损失和交叉熵损失，后者起伏更大，且后者更容易找到一个可用的最低点，从而达到优化的目的。
   -. Square Error（平方损失）
   -. Cross Entropy（交叉熵损失）
2. batch size是否合适？batch size太大 -> loss很快平稳，batch size太小 -> loss会震荡(理解mini-batch)
   (解决思路)采用合适的Mini-batch进行学习，使用Mini-batch的方法进行学习，一方面可以减少计算量，一方面有助于跳出局部最优点。因此要使用Mini-batch。更进一步，batch的选择非常重要，batch取太大会陷入局部最小值，batch取太小会抖动厉害
3. 是否选择了合适的激活函数？(各个激活函数的来源和差异)
   (解决思路)使用激活函数把卷积层输出结果做非线性映射，但是要选择合适的激活函数。
   -. Sigmoid函数是一个平滑函数，且具有连续性和可微性，它的最大优点就是非线性。但该函数的两端很缓，会带来猪队友的问题，易发生学不动的情况，产生梯度弥散。
   -. ReLU函数是如今设计神经网络时使用最广泛的激活函数，该函数为非线性映射，且简单，可缓解梯度弥散。
4. 学习率，学习率小收敛慢，学习率大loss震荡(怎么选取合适的学习率)
   (解决思路)学习率过大，会抖动厉害，导致没有优化提 , 学习率太小，下降太慢，训练会很慢
5. 是否选择了合适的优化算法？(比如Adam)(理解不同优化算法的适用场景)
   (解决思路)在梯度的基础上使用动量，有助于冲出局部最低点。

过拟合情况

1. Early Stopping(早停法)
   (详细解释)早停法将数据分成训练集和验证集，训练集用来计算梯度、更新权重和阈值，验证集用来估计误差，若训练集误差降低但验证集误差升高，则停止训练，同时返回具有最小验证集误差的连接权和阈值。
2. Regularization(正则化)
   (详细解释) 权重衰减(Weight Decay)。到训练的后期，通过衰减因子使权重的梯度下降地越来越缓。
   *. Batch Normalization
   *. Dropout
   *. L1 , L2
3. 调整网络结构
4. 增大训练数据量
   *. 获取更多的数据
   *. 数据扩充(图片: 镜像 , 翻转 , 随机裁剪等.)

优化器参数

torch.optim.Adam(model.parameters(), lr=lr ,eps=args.epsilon)

• params (iterable) – iterable of parameters to optimize or dicts defining parameter groups

• lr (float, optional) – learning rate (default: 1e-3)

• betas (Tuple[float, float], optional) – coefficients used for computing running averages of gradient and its square (default: (0.9, 0.999))

• eps (float, optional) – term added to the denominator to improve numerical stability (default: 1e-8)

• weight_decay (float, optional) – weight decay (L2 penalty) (default: 0)

• amsgrad (boolean, optional) – whether to use the AMSGrad variant of this algorithm from the paper On the Convergence of Adam and Beyond (default: False)

epsilon从0.1到1e-06,测试auc从0.6到0.9太可怕了，

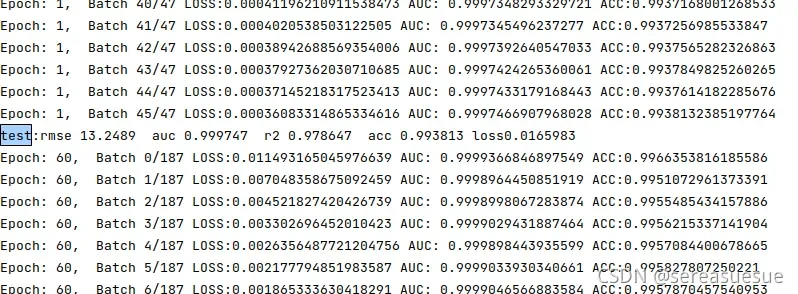
 torch.optim.Adam(model.parameters(), lr=lr,weight_decay=0.0005) 

加入weight_decay又到0.68附近

去掉weight_decay到测试的到0.88,训练集还在升高还往上升肯定有问题

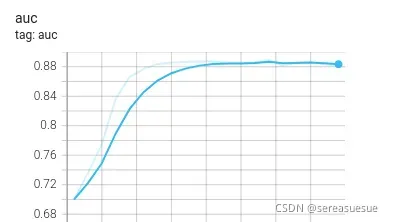
 自适应优化器Adam还需加learning-rate decay

自适应优化器Adam还需加learning-rate decay吗？ – 知乎

作者说加了lr decay的Adam还是有效提升了模型的表现。

但这只是在它的实验里进行了说明，并没有从理论上进行证明。因此不能说有定论，但是若你的模型结果极不稳定的问题，loss会抖动特别厉害，不妨尝试一下加个lr decay试一试。

如何加

torch中有很多进行lr decay的方式，这里给一个ExponentialLR API 的demo代码，就是这样就好了。

ExponentialLR原理： decayed_lr = lr * decay_rate ^ (global_step / decay_steps)

my_optim = Adam(model.parameters, lr)
decayRate = 0.96
my_lr_scheduler = torch.optim.lr_scheduler.ExponentialLR(optimizer=my_optim, gamma=decayRate)
#my_lr_scheduler = optim.lr_scheduler.StepLR(my_optim, step_size=lr_decay, gamma=decayRate)

for e in epochs:
    train_epoch()
    my_optim.step()

    valid_epoch()
    my_lr_scheduler.step()

学习率衰减策略 

pytorch必须掌握的的4种学习率衰减策略 – 知乎

优化器NoamOpt

我们选择Adam[1]作为优化器，其参数为 

和 . 根据以下公式，我们在训练过程中改变了学习率：

在预热中随步数线性地增加学习速率，并且此后与步数的反平方根成比例地减小它。我们设置预热步数为4000。

注意：这部分非常重要，需要这种设置训练模型。

class NoamOpt:
    "Optim wrapper that implements rate."
    def __init__(self, model_size, factor, warmup, optimizer):
        self.optimizer = optimizer
        self._step = 0
        self.warmup = warmup
        self.factor = factor
        self.model_size = model_size
        self._rate = 0
        
    def step(self):
        "Update parameters and rate"
        self._step += 1
        rate = self.rate()
        for p in self.optimizer.param_groups:
            p['lr'] = rate
        self._rate = rate
        self.optimizer.step()
        
    def rate(self, step = None):
        "Implement `lrate` above"
        if step is None:
            step = self._step
        return self.factor * \
            (self.model_size ** (-0.5) *
            min(step ** (-0.5), step * self.warmup ** (-1.5)))
        
def get_std_opt(model):
    return NoamOpt(model.src_embed[0].d_model, 2, 4000,
            torch.optim.Adam(model.parameters(), lr=0, betas=(0.9, 0.98), eps=1e-9))

当前模型在不同模型大小和超参数的情况下的曲线示例。

# Three settings of the lrate hyperparameters.
opts = [NoamOpt(512, 1, 4000, None), 
        NoamOpt(512, 1, 8000, None),
        NoamOpt(256, 1, 4000, None)]
plt.plot(np.arange(1, 20000), [[opt.rate(i) for opt in opts] for i in range(1, 20000)])
plt.legend(["512:4000", "512:8000", "256:4000"])
None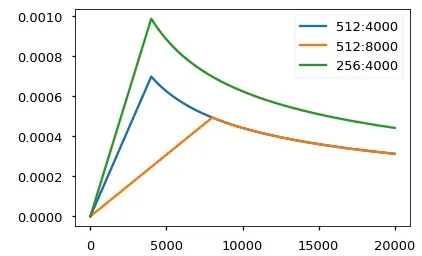

步数为4000是指，我使用时候设置为多大合适呢

loss为负

可能的原因：数据为归一化

网络中的：

self.softmax = nn.Softmax(dim=1)
改为：

self.softmax = nn.LogSoftmax(dim=1)

测试集AUC高于训练集AUC

 感觉这个回答似乎有些道理，我的数据集划分的时候可能没有随机打乱