不小心提前放出来了，同样在第九期的同学们小心！

1、信息矩阵分析

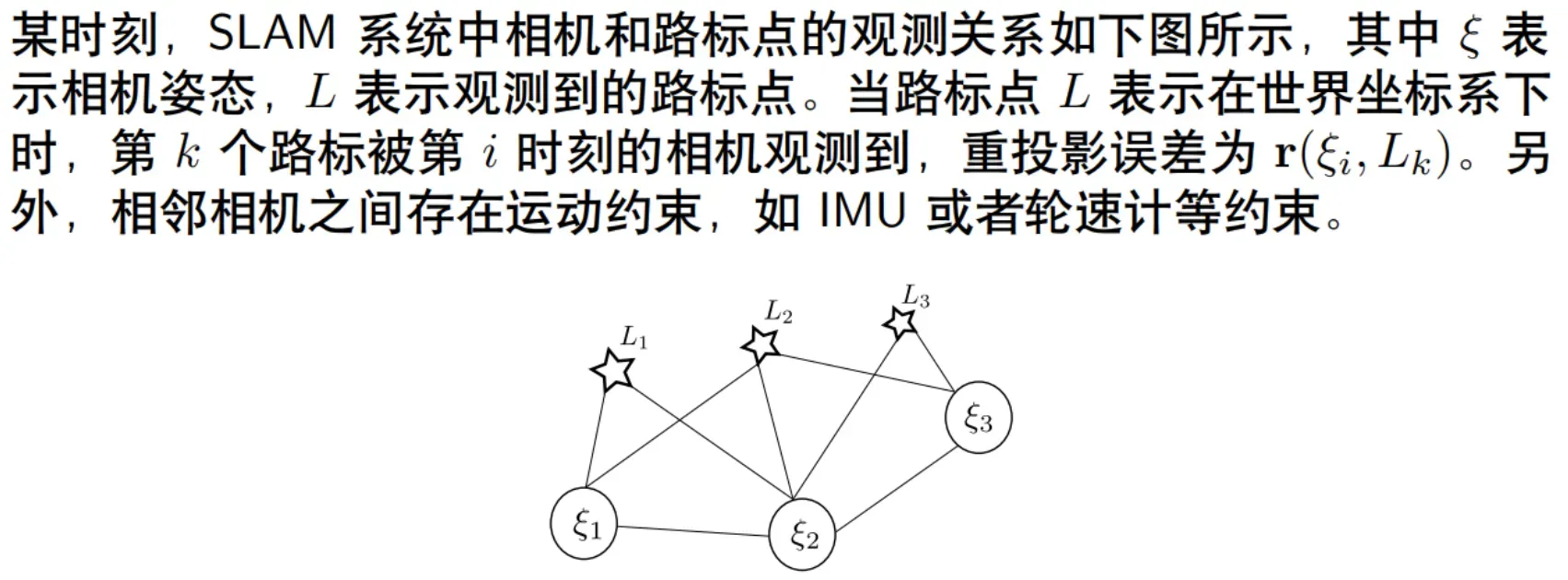
1.1 绘制上述系统的信息矩阵Λ

雅各比：

高斯-牛顿增量方程：

例如：

对应的信息矩阵为


从得到的信息矩阵如下：

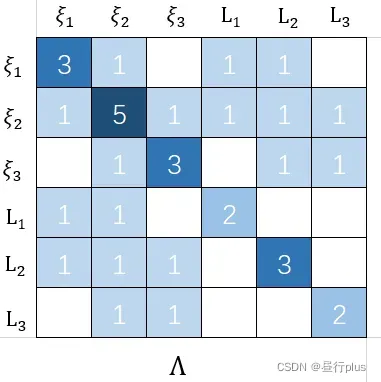
其实可以直接根据变量之间的关系给出。上面的公式只是一个理论说明。

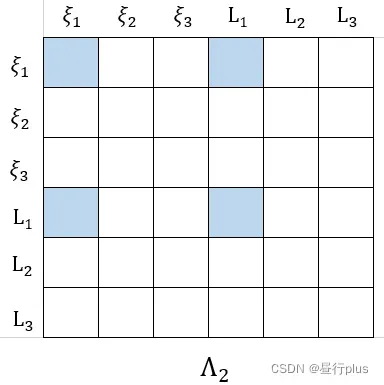
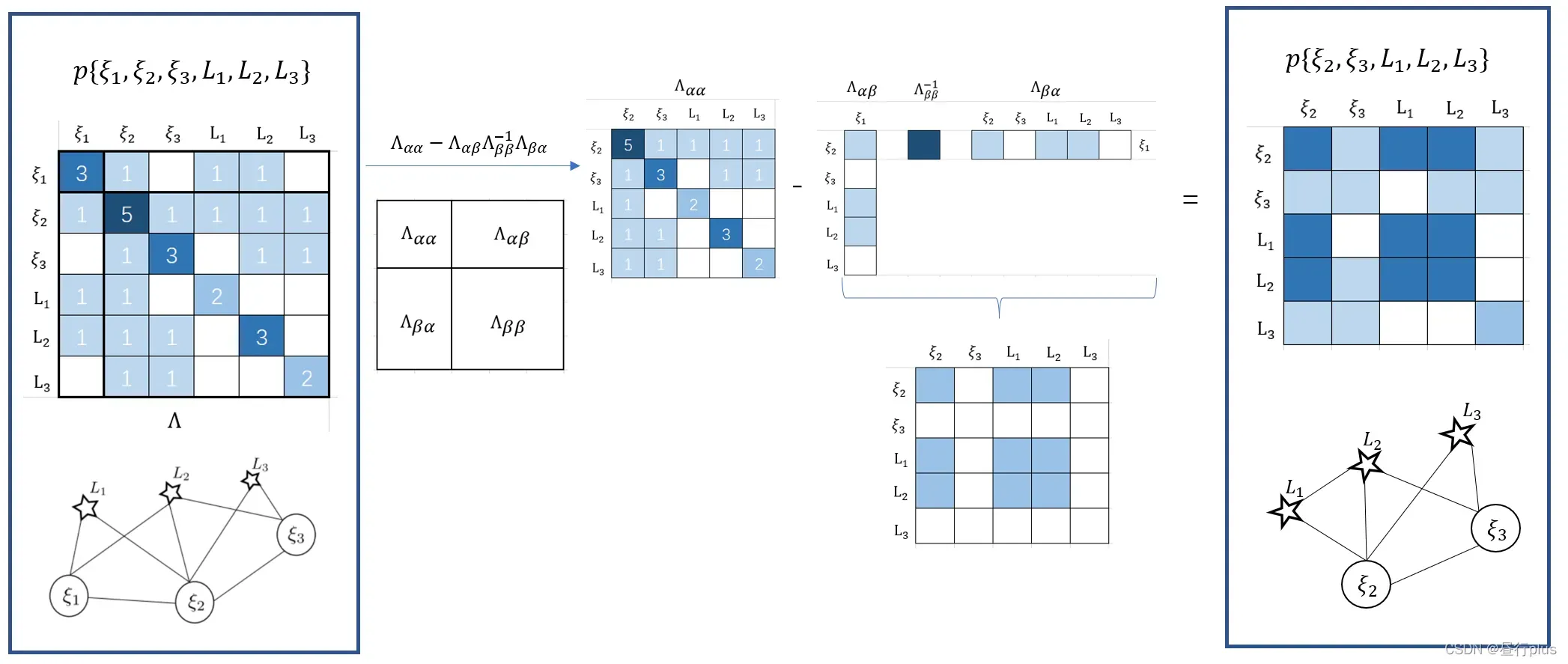
1.2 绘制相机被 marg 以后的信息矩阵Λ′

参考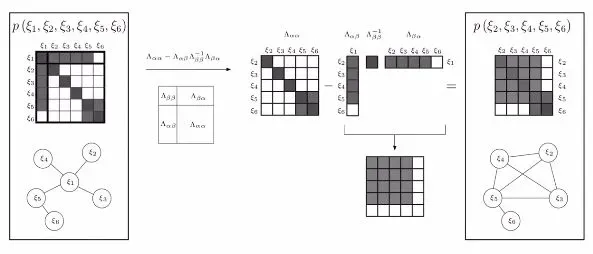

得到相机被 marg 以后的信息矩阵:

2、证明信息矩阵和协方差的逆之间的关系

阅读《Relationship between the Hessian and Covariance Matrix for Gaussian Random Variables》 证明信息矩阵和协方差的逆之间的关系

证明一

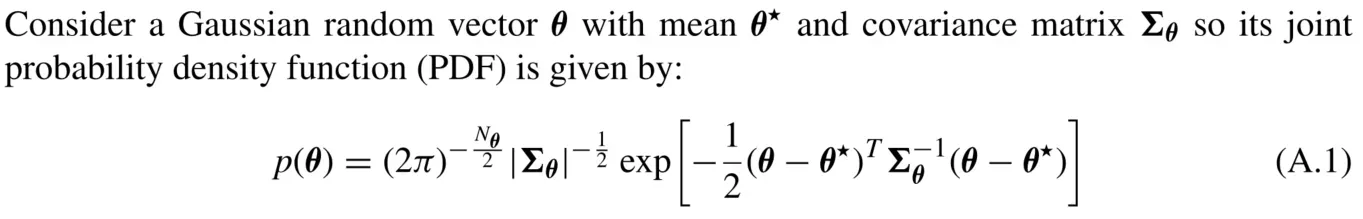
对其取负对数得到负对数似然（Negative Log Likelihood）函数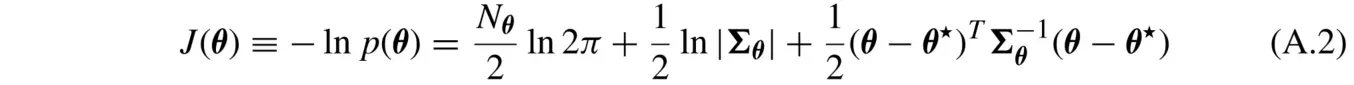

将上式（A.2） 看作二次函数的二阶泰勒展开（关于海塞矩阵和泰勒展开），则

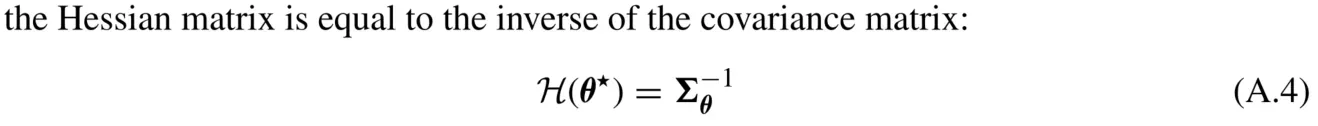
公式(A.4)的等号是建立在是的线性函数的基础上的；
如果是非线性函数，泰勒展开式会有三阶以上的项，所以应该是近似等号。
总结如下：

当高斯分布的均值是关于状态的线性函数时，negative log likelihood的二阶导数（也就是其Hessian），正好是这个线性变换后的新状态的的协方差的逆，此时也有Hessian of Negative Log Likelihood (about the original state) = Inverse of (new) Covariance Matrix。
当高斯分布的均值是关于状态的非线性函数时，可以做一个线性化将其展开乘线性形式，于是 Approximate Hessian of Negative Log Likelihood (about the original state) = Approximate Inverse of (new) Covariance MatrixInverse of (new) Covariance Matrix。
原文来自：https://www.cnblogs.com/xiaochen-qiu/p/11170487.html

现在问题变成了证明信息矩阵与Hessian矩阵相等
这个外语博客证明了这一点（全英文警告！）

证据二

设 n 维高斯随机变量
其概率密度函数为：

即上式（A.1）的。
由于分母与无关，令得

根据wiki中信息矩阵的定义：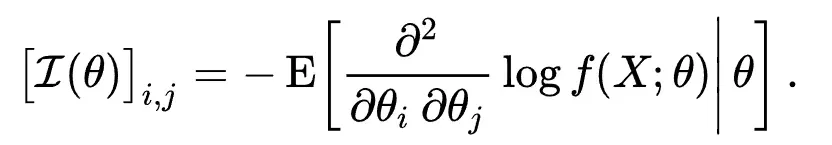

这里和应该是一样的。为了计算方便，我们写：

和

所以

所以

即信息矩阵=协方差矩阵的逆

参考多维高斯随机变量的信息矩阵与协方差矩阵的关系

3、编程题

请补充作业代码中单目 Bundle Adjustment 信息矩阵的计算，并输出正确的结果。

正确的结果为：奇异值最后 7 维接近于 0，表明零空间的维度为 7

3.1 原理分析

补充内容是Hessian矩阵，在此之前需要得到雅可比矩阵。涉及雅可比行列式的代码有两种：

1、jacobian_Pj：重投影误差（观测方程）对特征点（表示在世界坐标系下）的雅克比矩阵
2、jacobian_Ti：表示重投影误差（观测方程）对相机位姿的雅克比矩阵。

涉及的具体代码如下：

参考十四讲第二版p186-p197
在世界坐标系中标记地标点，其在相机坐标系中的坐标为，即

容易得到重投影误差对的雅可比， 也即代码中的jacobian_uv_Pc

对于jacobian_Pj，通过链式法则有：

而重投影误差对相机位姿的雅可比jacobian_Ti为：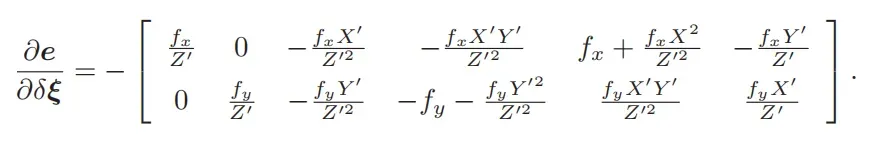

如果的定义是平移前后旋转，那么矩阵的前三列可以与后三列互换。
代码正是这样做的。
公式推导可见博客第4题，第2问。

Hessian矩阵的计算类似于第一题的信息矩阵分析。

3.2 代码内容

hessian_nullspace_test.cpp

//
// Created by daybeha on 22-03-05.
//
#include <iostream>
#include <vector>
#include <random>  
#include <Eigen/Core>
#include <Eigen/Geometry>
#include <Eigen/Eigenvalues>

struct Pose
{
    Pose(Eigen::Matrix3d R, Eigen::Vector3d t):Rwc(R),qwc(R),twc(t) {};
    Eigen::Matrix3d Rwc;
    Eigen::Quaterniond qwc;
    Eigen::Vector3d twc;
};
int main()
{
    int featureNums = 20;
    int poseNums = 10;
    int diem = poseNums * 6 + featureNums * 3;
    double fx = 1.;
    double fy = 1.;
    Eigen::MatrixXd H(diem,diem);
    H.setZero();

    std::vector<Pose> camera_pose;
    double radius = 8;
    for(int n = 0; n < poseNums; ++n ) {
        double theta = n * 2 * M_PI / ( poseNums * 4); // 1/4 圆弧
        // 绕 z轴 旋转
        Eigen::Matrix3d R;
        R = Eigen::AngleAxisd(theta, Eigen::Vector3d::UnitZ());
        Eigen::Vector3d t = Eigen::Vector3d(radius * cos(theta) - radius, radius * sin(theta), 1 * sin(2 * theta));
        camera_pose.push_back(Pose(R,t));
    }

    // 随机数生成三维特征点
    std::default_random_engine generator;
    std::vector<Eigen::Vector3d> points;
    for(int j = 0; j < featureNums; ++j)
    {
        //连续均匀分布
        //http://c.biancheng.net/view/640.html
        std::uniform_real_distribution<double> xy_rand(-4, 4.0);
        std::uniform_real_distribution<double> z_rand(8., 10.);
        double tx = xy_rand(generator);
        double ty = xy_rand(generator);
        double tz = z_rand(generator);

        Eigen::Vector3d Pw(tx, ty, tz);
        points.push_back(Pw);

        for (int i = 0; i < poseNums; ++i) {
            Eigen::Matrix3d Rcw = camera_pose[i].Rwc.transpose();
            Eigen::Vector3d Pc = Rcw * (Pw - camera_pose[i].twc);

            double x = Pc.x();
            double y = Pc.y();
            double z = Pc.z();
            double z_2 = z * z;
            Eigen::Matrix<double,2,3> jacobian_uv_Pc;
            jacobian_uv_Pc<< fx/z, 0 , -x * fx/z_2,  //重投影误差对特征点的雅可比（相机坐标）
                    0, fy/z, -y * fy/z_2;
            //重投影误差对特征点的雅可比（世界坐标）
            Eigen::Matrix<double,2,3> jacobian_Pj = jacobian_uv_Pc * Rcw;
            //重投影误差对相机位姿的雅可比
            Eigen::Matrix<double,2,6> jacobian_Ti;
            jacobian_Ti << -x* y * fx/z_2, (1+ x*x/z_2)*fx, -y/z*fx, fx/z, 0 , -x * fx/z_2,
                            -(1+y*y/z_2)*fy, x*y/z_2 * fy, x/z * fy, 0,fy/z, -y * fy/z_2;

            H.block(i*6,i*6,6,6) += jacobian_Ti.transpose() * jacobian_Ti;
            /// 请补充完整作业信息矩阵块的计算
            H.block(i*6, poseNums * 6 + j * 3, 6, 3) +=jacobian_Ti.transpose() * jacobian_Pj;
            H.block(poseNums * 6 + j * 3, i*6, 3,6) += jacobian_Pj.transpose() * jacobian_Ti;
            H.block(poseNums * 6 + j * 3, poseNums * 6 + j * 3, 3, 3) += jacobian_Pj.transpose() * jacobian_Pj;
        }
    }

//    std::cout << H << std::endl;
//    Eigen::SelfAdjointEigenSolver<Eigen::MatrixXd> saes(H);
//    std::cout << saes.eigenvalues() <<std::endl;

    Eigen::JacobiSVD<Eigen::MatrixXd> svd(H, Eigen::ComputeThinU | Eigen::ComputeThinV);
    std::cout << svd.singularValues() <<std::endl;
  
    return 0;
}

新增内容：

H.block(i*6, poseNums * 6 + j * 3, 6, 3) +=jacobian_Ti.transpose() * jacobian_Pj;
H.block(poseNums * 6 + j * 3, i*6, 3,6) += jacobian_Pj.transpose() * jacobian_Ti;
H.block(poseNums * 6 + j * 3, poseNums * 6 + j * 3, 3, 3) += jacobian_Pj.transpose() * jacobian_Pj;

代码输出：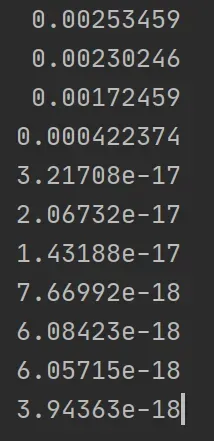

拓展笔记 – 奇异值分解（SVD, singular value decomposition）

如果你和我一样基础较弱，肯定对svd.singularValues()有疑问，它返回的是什么?

奇异值

什么是奇异值？没有任何意义？

找一个更生动的关于奇异值的链接，我会删掉一些我认为更重要的部分：
奇异值分解的几何意义是：对于任意一个矩阵，我们需要找到一组二乘二正交的单位向量序列，使得矩阵作用于这个向量序列后，得到一个新的向量序列，保持二乘二正交性。奇异值的几何意义是：经过这组变换后新向量序列的长度。

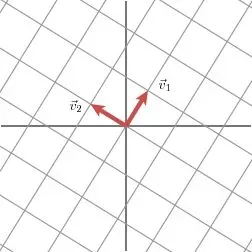
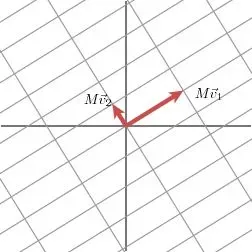
如上图，
向量和分别是的左右奇异向量
另外，奇异值具有大于零的性质，一般从大到小排列：

另外两个关于奇异值分解的更详细的博客：
奇异值分解的秘密（一）：矩阵的奇异值分解过程
奇异值分解的秘密（二）：降维和奇异向量的意义

为什么说奇异值最后 7 维接近于 0就表明零空间的维度为 7？什么是零空间维度？

对于零空间，wiki中的定义为：一个算子的零空间是方程的所有解的集合
那么这很清楚：
根据奇异值的公式：，当为0时，公式变为，
那么对应于的右奇异向量的集合就是零空间
又因为有7个奇异值为0，那么就有7个自由度， 因此对应零空间维度为7（参考）

参考

从零手写VIO——（四）基于滑动窗口算法的 VIO 系统：可观性和一致性（上）舒尔补
从零手写VIO——（四）基于滑动窗口算法的 VIO 系统：可观性和一致性（下）滑动窗口算法
手写VIO总结（四）
手写VIO课后作业（四）
从零开始手写VIO第四章作业（含关键点的参考资料）
深蓝学院《从零开始手写VIO》作业4
深蓝学院《从零开始手写VIO》作业四
YouDao Cloud Note
高翔，张涛等《视觉SLAM十四讲》p186-p197

舒尔布
Schur complement
雅可比矩阵、黑森矩阵、泰勒展开
Fisher information
多维高斯随机变量信息矩阵与协方差矩阵的关系
【原创】极大似然估计中，信息矩阵、Hessian矩阵和协方差矩阵的关系