4.5 全连接层
全连接层是一个列向量(单个样本)。通常用于图像分类任务的深度神经网络的后期层。
全连接层是每个节点都连接到前一层的所有节点,用来合成前面提取的特征。由于其全连接的特性,全连接层的参数一般是最多的。
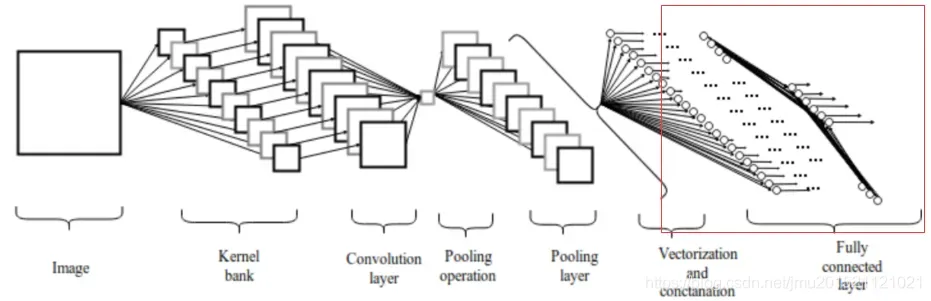
全连接层(fully connected layers,FC)在整个卷积神经网络中起到“分类器”的作用。如果说卷积层、池化层和激活函数等操作是将原始数据映射到隐层特征空间的话,全连接层则起到将学到的“分布式特征表示”。映射到样本标记空间的作用。
全连接层将特征提取得到的高维特征图映射成一维特征向量,该向量包含所有特征信息,可以转化为最终分类到各个类别的概率。
转自:https://blog.csdn.net/qq_39521554/article/details/81385159
举个栗子:
现在全连接层得到一个3x3x5x4096的输出,经过全连接层后,输出一个1x1x4096x1的一维向量

那它是怎么样把3x3x5x4096的输出,转换成1x1x4096x1的形式?很简单,可以理解为在中间做了一个卷积。
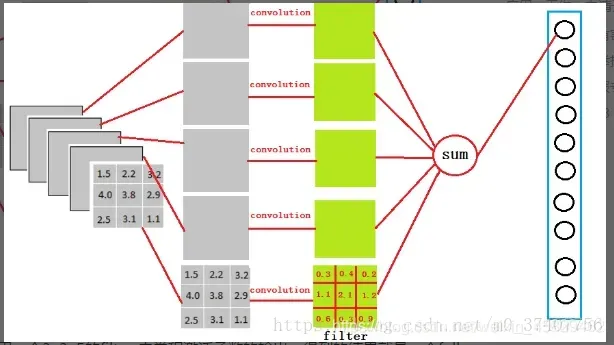
从上图我们可以看出,我们用一个3x3x5的filter 去卷积激活函数的输出,得到的结果就是一个fully connected layer 的一个神经元的输出,这个输出就是一个值。因为我们有4096个神经元。我们实际就是用一个3x3x5x4096的卷积层去卷积激活函数的输出。
再比如:我们想找出图片中是否有猫,可以使用训练好的卷积核对原图进行卷积,根据输出进行判断。
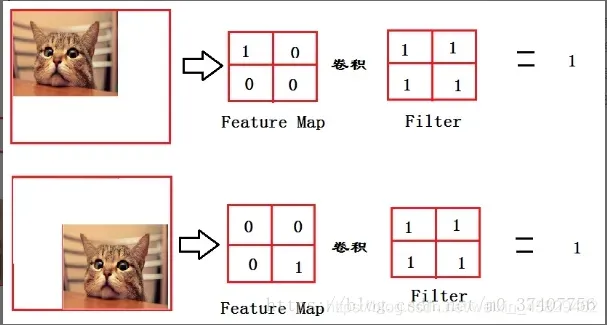
从上图我们可以看出,猫在不同的位置,输出的feature值相同,但是位置不同。
对于计算机来说,如果特征值相同,但特征值位置不同,分类结果也可能不同。
这时全连接层filter的作用就相当于
喵在哪我不管,我只要喵,于是我让filter去把这个喵找到,
实际就是把feature map 整合成一个值,这个值大,有喵,这个值小,那就可能没喵
和这只猫在哪里关系不大,鲁棒性大大增强。
因为空间结构特性被忽略了,所以全连接层不适合用于在方位上找Pattern的任务,比如segmentation。
全连接层的一层神经元可以看成是一个多项式(类似于加权平均),我们使用很多神经元来拟合数据分布
但是只用一层fully connected layer 有时候没法解决非线性问题,
而如果有两层或以上fully connected layer就可以很好地解决非线性问题了
转载自:https://zhuanlan.zhihu.com/p/33841176
在实际使用中,全连接层可以通过卷积操作来实现:
- 对前层是全连接的全连接层可以转化为卷积核为1×1的卷积;
- 而前层是卷积层的全连接层可以转化为卷积核为 h*w 的全局卷积, h*w 分别为前层卷积结果的高和宽。
全连接的核心操作就是矩阵向量乘积 y = Wx
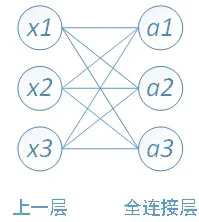
其中,x1、x2、x3为全连接层的输入,a1、a2、a3为输出,
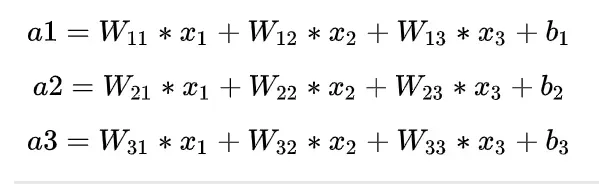
注:本文内容来自书籍和网络,仅供个人学习笔记使用
文章出处登录后可见!
