基于Bundle Adjustment 的VIO融合

什么是Bundle Adjustment

Bundle Adjustment( BA )，是指从视觉图像中提炼出最优的3D模型和相机参数(内参数和外参数)。考虑从任意特征点发射出来的几束光线( bundles of light rays),它们会在几个相机的成像平面上变成像素或是检测到的特征点。如果我们调整( adjustment)各相机姿态和各特征点的空间位置，使得这些光线最终收束到相机的光心，就称为BA（光束法平差）。bundle adjustment 其本质还是离不开最小二乘原理(几乎所有优化问题其本质都是最小二乘)，目前bundle adjustment 优化框架最为代表的是ceres solver和g2o。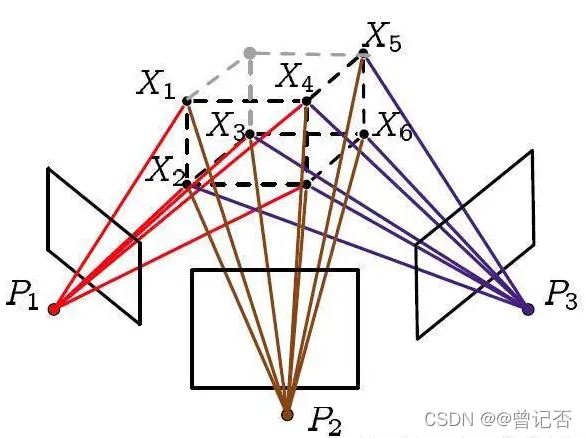

如上图所示相机分别分三次在P1；P2；P3处进行拍摄（三维空间中的物体在二维相机底片上的投影）那现在就该说下什么叫重投影误差了，重投影也就是指的第二次投影，那到底是怎么投影的呢？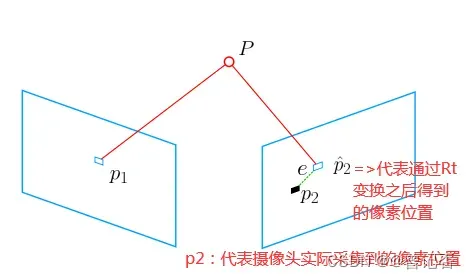

让我们整理一下：

• 其实第一次投影是指相机拍照时，将三维空间点投影到图像上，然后我们用这些图像对一些特征点进行三角剖分，利用几何信息构造三角形来确定图像的位置三维空间点（相关内容请参考对极几何）；
  
• 最后用我们计算的三维点的坐标（注意不是真实的）和我们计算的相机矩阵（当然不是真实的）进行第二次投影，也就是reprojection，然后计算坐标；
  
• 既然我们知道了重投影是什么，那么重投影误差是什么类型的误差呢？
  这个误差是指的真实三维空间点在图像平面上的投影（也就是图像上的像素点）和重投影（其实是用我们的计算值得到的虚拟的像素点）的差值，因为种种原因计算得到的值和实际情况不会完全相符，也就是这个差值不可能恰好为0，此时也就需要将这些差值的和最小化获取最优的相机参数及三维空间点的坐标。
  
  

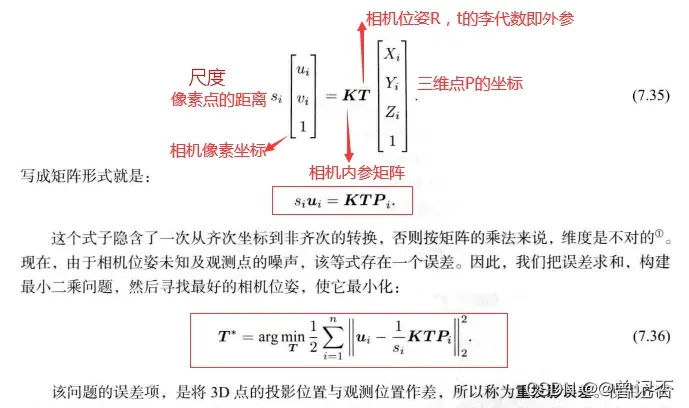
Bundle Adjustment的作用

BA不仅可以优化位姿（R和t），还可以优化特征点的空间位置。而我们又可以把BA看成是最小化重投影误差（Reprojection error）问题，同时这也是一个非线性最小二乘问题。BA属于SLAM中的后端，BA就是一个优化模型，其本质就是最小化重投影误差。

后端优化中重投影误差函数/BA问题

在视觉SLAM中，我们通过最小化路标点的重投影误差，实现对相机位姿的约束。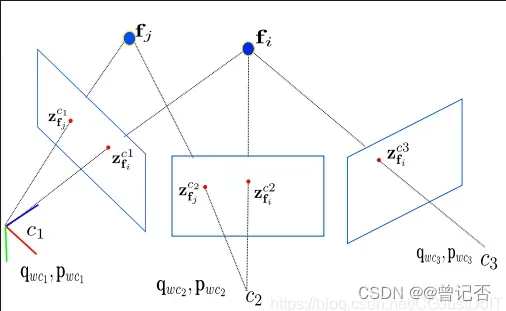

对于VSLAM中的BA问题，有以下已知条件：

• 状态量初始值：特征点的三维坐标；相机的姿势
  
• 系统测量：不同图像上特征点的像素坐标
  

BA问题就是如何利用测量值来实现对初始状态量的最优估计？

• 构造误差函数，通过最小二乘法得到状态量的最优估计，使重投影误差最小。 （理论预测值减去实际观测值）
  
  符号定义：
  
• q: 旋转四元数
  
• p: 平移向量
  
• : 特征点 3D 坐标
  
• ：摄像系统
  
• ：投影功能
  
• 观察
  
• 规范
  

VIO信息融合考虑的问题

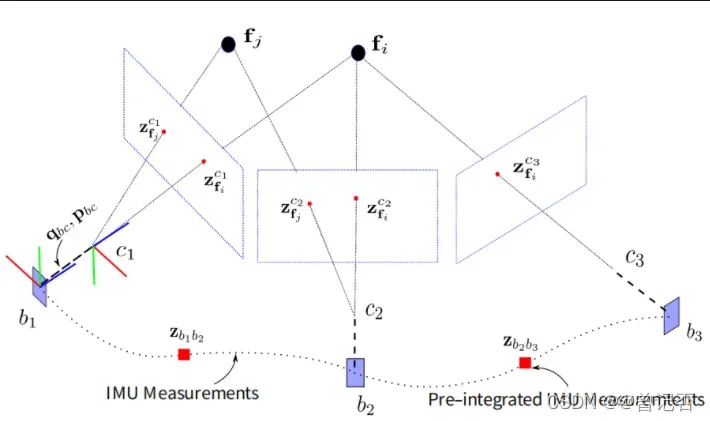
将IMU融入到视觉里程计中，除了要最小化特征点的重投影误差以外，还需要考虑如下问题：

1. 相机与IMU的外参，包括旋转和平移
   
2. 相机和IMU的帧率不同，如何实现两者数据上的融合
   
3. IMU从到时，有测量值，如何构建IMU的测量误差函数
   
4. 位姿的来源有IMU测量和视觉测量，如何设定多个信息源权重
   
5. 融合信息后构造的误差函数如何解决
   

解决最小二乘问题

线性最小二乘解：最速下降法和牛顿法

非线性线性最小二乘解：Gauss-Newton 和 LM

最小二乘中遇到 outlier，通过添加鲁棒核函数

定义：

找到一个维变量，使损失函数取局部最小值：

其中为残差函数，如实测值与预测值之差，有。局部最小值意味着任何都有

假设损失函数

其中，和分别是损失函数对变量的一阶导数和二阶导数矩阵。
忽略泰勒展开的高阶项，损失函数变成二次函数，可以很容易地得到以下性质：

• 如果在点；处有导数为0，则称这个点为稳定点。
  
• 在点x,处对应的Hessian为H；
  
• 如果是正定矩阵，即它的特征值都大于0，则在处有F(x)为
  局部最小值；
  
• 如果是负定矩阵，即它的特征值都小于0，则在处有F(x)为
  局部最大值；
  
• 如果是不定矩阵，即它的特征值大于0也有小于0的，则处
  是鞍点。
  

基础知识：最速下降法、牛顿法

迭代下降

找到一个下降方向，使损失函数随着的迭代逐渐减小，直到收敛到：

分为两步：一是求下降方向的单位向量，二是确定下降步长。
假设足够小，我们可以对损失函数进行一阶泰勒展开：

只需寻找下降方向并满足：

通过 line search 方法找到下降的步长：

最速下降法——适用于迭代的开始

从下降方向的条件可知：表示下降方向与梯度方向的夹角。当时，有

即梯度的负方向是下降最快的方向。
缺点：在最优值附近振荡，收敛慢。

牛顿法——适用于接近最优值

在局部最优点附近，如果是最优解，则损失函数对的导数等于 0 ，对损失函数取一阶导有：

得到：。
缺点：二阶导数矩阵的计算比较复杂。

阻尼法

将损失函数的二阶泰勒展开表示为

求以下函数的最小化：

其中，为阻尼因子，是惩罚项。 对新的损失函数求一阶导，并令其等于 0 有:

进阶:高斯牛顿法，LM算法的具体实现

非线性最小二乘

1、符号说明
对于公式简化，可以将残差组合成向量形式。

然后有：
同样，如果你还记得，有：

2、基础
残差函数为非线性函数，其一阶泰勒近似有：

特别注意这里的是残差函数的雅可比矩阵。代入损失函数：

这样，损失函数近似为二次函数，如果雅克比是满秩，则正定，损失函数有最小值。
另外，很容易获得：和

高斯-牛顿法

令公式 (1) 的一阶导等于 0 ，得到：

上式一般见于论文

LM算法

Levenberg (1944) 和 Marquardt (1963) 先后对高斯牛顿法进行了改进， 求解过程中引入了阻尼因子:

疑问: LM 中阻尼因子有什么作用，它怎么设定呢?

1、阻尼因子的作用：

• 保证正定，迭代向下进行。
  
• 很大，那么，接近最速下降法。
  
• 比较小，则，接近高斯-牛顿法。
  
• 阻尼因子的大小与的元素有关。正半定信息矩阵
  

2、阻尼因子初始值选取
特征值和对应的特征向量为。经过的特征值分解，我们有：可以得到：

所以，一个简单的初值策略是：

通常根据需要设置。

在工程中，常取与的最大特征值的数量级一致：对角元素的最大值的数量级一致。

3、阻尼因子的更新策略
定性分析、直观感受阻尼系数的更新：
(1) 如果，则, 增大阻尼减小步长，拒绝本次迭代。
(2) 如果, 则, 减小阻尼增大步长。加快收敛，减少迭代次数。
定量分析、阻尼因子更新策略由缩放因子决定：

在：

首先比例因子分母始终大于 0 , 如果:

• ，则，应为，增大阻尼，减小步长。
  
• 如果且比较大，减小, 让 LM 接近 Gauss-Newton 使得系 统更快收敛。
  
• 反之，如果是比较小的正数，则增大阻尼，减小迭代步长。
  1963 年 Marquardt 提出了一个如下的阻尼策略:
  
  

L-M 迭代法算法步骤

L-M 优化公式:

1. 设置初始状态量的初始值，计算收敛阈值和阻尼因子
   
2. 使用系统的所有状态变量和测量数据分别计算残差和，并将它们整合到
   
3. 计算残差函数 计算关于状态向量 的雅可比矩阵
   
4. 解方程，我们得到
   
5. 计算实际drop和近似drop的比例因子，判断迭代成功。如果 ,
   更新，否则
   
6. 判断, 若成立则结束; 不成立, 重复 2-5 步
   

终极：实现健壮的内核功能

引言：最小二乘中遇到 outlier 怎么处理? 核函数如何在代码中实现?
有多种方法 ，这里主要介绍 g2o 和 ceres 中使用的 Triggs Correction 。
Iriggs Correction
鲁棒核函数直接作用于残差，最小二乘函数变为如下形式：

将误差的平方项记为，则鲁棒核误差函数的二阶泰勒展开如下：

上述函数中的计算稍微复杂一点：

将上式代入上式有：

对上式求和后，对变量求导，令其等于 0 ，得到:

Example Cauchy Cost Function
柯西鲁棒核函数的定义为：

其中，为控制参数。 的一阶和二阶导数是：