原文标题 :Batch Norm Explained Visually — How it works, and why neural networks need it
动手教程,直观的深度学习系列[0]
可视化解释 Batch Norm — 它是如何工作的,以及为什么神经网络需要它
一个非常重要的深度学习层的温和指南,用简单的英语

Batch Norm 是现代深度学习从业者工具包的重要组成部分。在 Batch Normalization 论文中介绍它后不久,它被认为在创建可以更快训练的更深层次的神经网络方面具有变革性。[0]
Batch Norm 是一种神经网络层,现在在许多架构中普遍使用。它通常作为线性或卷积块的一部分添加,有助于在训练期间稳定网络。
在本文中,我们将探讨 Batch Norm 是什么、为什么需要它以及它是如何工作的。
您可能还喜欢阅读我关于 Batch Norm 的另一篇文章,该文章解释了 Batch Norm 为何如此有效。
如果你对一般的神经网络架构感兴趣,我还有一些你可能喜欢的其他文章。
但在我们讨论批标准化本身之前,让我们先了解一下标准化的背景。
Normalizing Input Data
将数据输入深度学习模型时,标准做法是将数据归一化为零均值和单位方差。这是什么意思,我们为什么要这样做?
假设输入数据由几个特征 x1、x2、…xn 组成。每个特征可能有不同的值范围。例如,特征 x1 的值可能介于 1 到 5 之间,而特征 x2 的值可能介于 1000 到 99999 之间。
因此,对于每个特征列,我们分别取数据集中所有样本的值并计算均值和方差。然后使用下面的公式对值进行标准化。
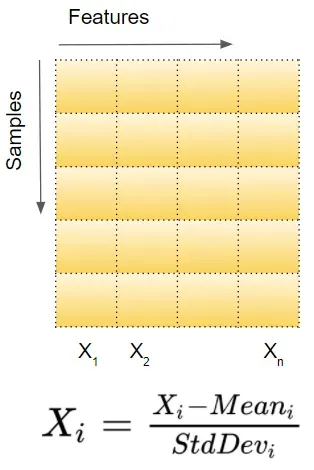
在下图中,我们可以看到归一化数据的效果。原始值(蓝色)现在以零为中心(红色)。这可确保所有特征值现在都处于相同的比例。
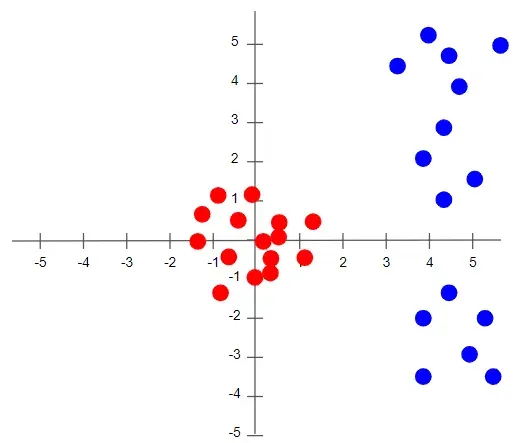
为了理解没有归一化会发生什么,让我们看一个只有两个不同尺度的特征的例子。由于网络输出是每个特征向量的线性组合,这意味着网络学习每个特征的权重,这些权重也在不同的尺度上。否则,大特征只会淹没小特征。
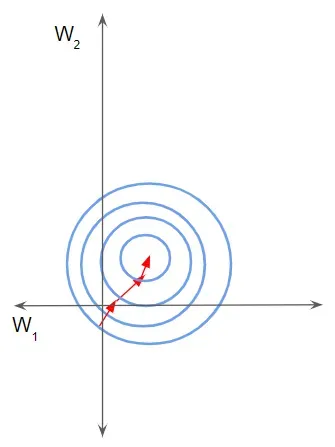
然后在梯度下降期间,为了“移动”损失,网络将不得不对一个权重与另一个权重相比进行大量更新。这会导致梯度下降轨迹沿一维来回振荡,从而采取更多步骤来达到最小值。
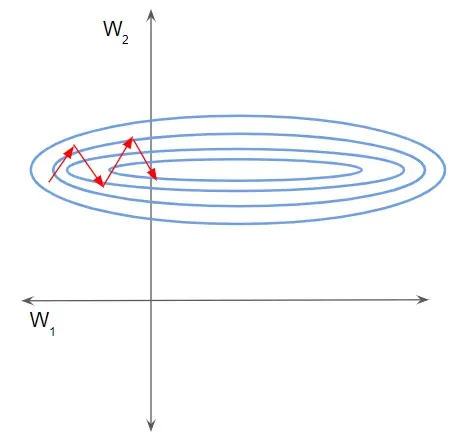
在这种情况下,损失景观看起来像一条狭窄的沟壑。我们可以沿二维分解梯度。它在一个维度上是陡峭的,而在另一个维度上更平缓。
由于梯度较大,我们最终对一个权重进行了较大的更新。这会导致梯度下降反弹到斜坡的另一侧。另一方面,沿第二个方向的较小梯度导致我们进行较小的权重更新,从而采取较小的步长。这种不均匀的轨迹需要更长的时间才能使网络收敛。
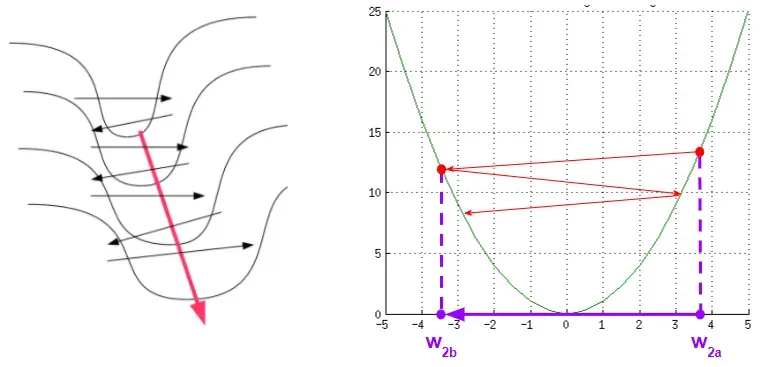
相反,如果特征在相同的尺度上,损失景观会像碗一样更均匀。然后梯度下降可以平稳地下降到最小值。
如果您想了解更多相关信息,请参阅我的神经网络优化器,其中更详细地解释了这一点,以及不同的优化器算法如何演变以应对这些挑战。
批量规范的必要性
既然我们了解了 Normalization 是什么,那么需要 Batch Normalization 的原因就开始变得清晰了。
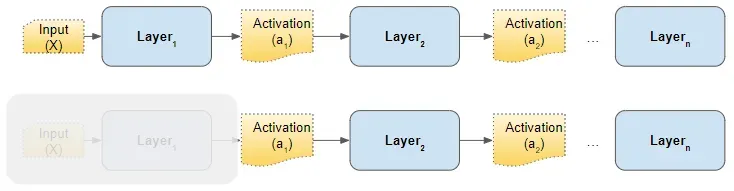
考虑网络的任何隐藏层。前一层的激活只是这一层的输入。例如,从下图中的第 2 层的角度来看,如果我们“清除”所有先前的层,则来自第 1 层的激活与原始输入没有什么不同。
要求我们对第一层的输入进行归一化的相同逻辑也适用于这些隐藏层中的每一个。
换句话说,如果我们能够以某种方式对前一层的激活进行归一化,那么梯度下降将在训练期间更好地收敛。这正是 Batch Norm 层为我们所做的。
批处理规范如何工作?
Batch Norm 只是插入隐藏层和下一个隐藏层之间的另一个网络层。它的工作是从第一个隐藏层获取输出并对其进行归一化,然后将它们作为下一个隐藏层的输入传递。

就像任何网络层的参数(例如权重、偏差)一样,Batch Norm 层也有自己的参数:
- 两个可学习的参数称为 beta 和 gamma。
- 两个不可学习的参数(平均移动平均线和方差移动平均线)被保存为 Batch Norm 层的“状态”的一部分。
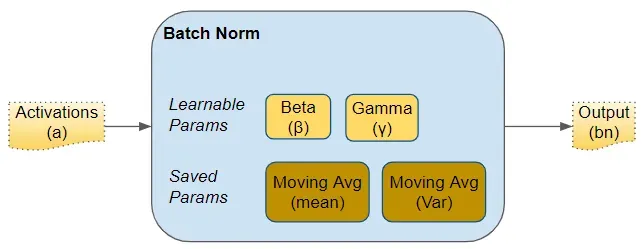
这些参数是每个 Batch Norm 层的。因此,如果我们在网络中有 3 个隐藏层和 3 个 Batch Norm 层,则这三层将有 3 个可学习的 beta 和 gamma 参数。对于移动平均线参数也是如此。

在训练期间,我们一次向网络提供一小批数据。在前向传递期间,网络的每一层都会处理该小批量数据。 Batch Norm 层按如下方式处理其数据:
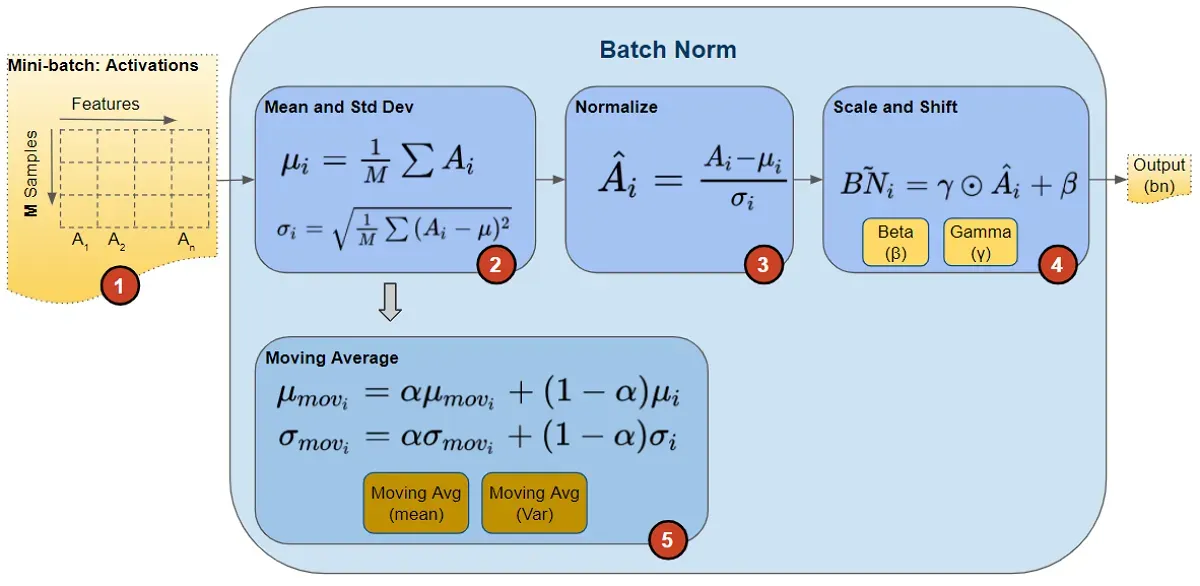
1. Activations
来自前一层的激活作为输入传递给 Batch Norm。数据中的每个特征都有一个激活向量。
2. 计算均值和方差
对于每个激活向量,分别计算小批量中所有值的均值和方差。
3. Normalize
使用相应的均值和方差计算每个激活特征向量的归一化值。这些归一化值现在具有零均值和单位方差。
4. Scale and Shift
这一步是 Batch Norm 引入的巨大创新,赋予了它强大的功能。与要求所有归一化值的均值和单位方差为零的输入层不同,Batch Norm 允许将其值移动(到不同的均值)和缩放(到不同的方差)。它通过将归一化值乘以一个因子 gamma 并添加一个因子 beta 来实现这一点。请注意,这是逐元素乘法,而不是矩阵乘法。
这种创新的巧妙之处在于,这些因素不是超参数(即模型设计者提供的常数),而是网络学习的可训练参数。换句话说,每个 Batch Norm 层都能够为自己找到最佳因素,因此可以移动和缩放归一化值以获得最佳预测。
5. Moving Average
此外,Batch Norm 还保留均值和方差的指数移动平均线 (EMA) 的运行计数。在训练期间,它只是计算这个 EMA,但不做任何事情。在训练结束时,它只是将此值保存为层状态的一部分,以在推理阶段使用。
稍后我们讨论推理时会回到这一点。移动平均线计算使用标量“动量”,用下面的 alpha 表示。这是一个仅用于 Batch Norm 移动平均值的超参数,不应与优化器中使用的动量混淆。
Vector Shapes
下面,我们可以看到这些向量的形状。计算特定特征的向量所涉及的值也以红色突出显示。但是,请记住,所有特征向量都是在单个矩阵运算中计算的。
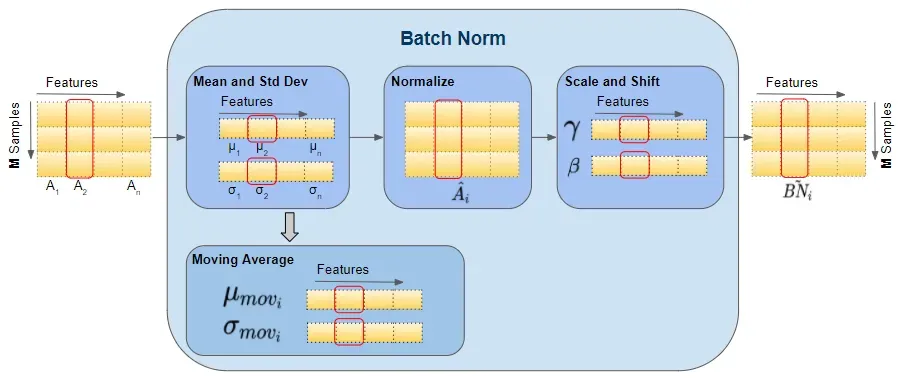
在向前传球之后,我们照常进行向后传球。计算梯度并为所有层权重以及 Batch Norm 层中的所有 beta 和 gamma 参数进行更新。
推理期间的批量标准化
正如我们上面所讨论的,在训练期间,Batch Norm 从计算 mini-batch 的均值和方差开始。但是,在推理期间,我们只有一个样本,而不是小批量。在这种情况下,我们如何获得均值和方差?
这是两个移动平均线参数的用武之地——我们在训练期间计算并与模型一起保存的参数。我们在推理过程中将这些保存的均值和方差值用于批量范数。
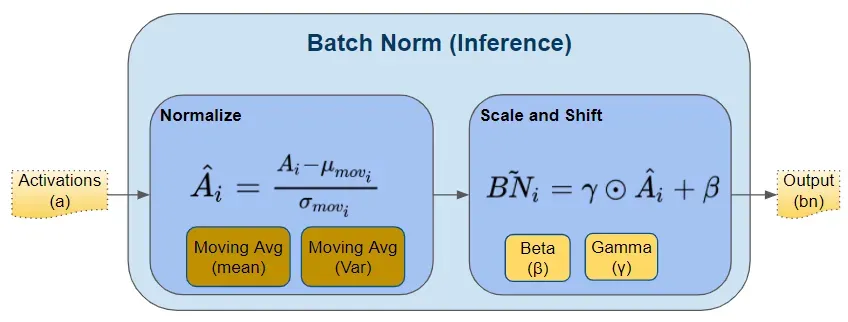
理想情况下,在训练期间,我们可以计算并保存完整数据的均值和方差。但这将非常昂贵,因为我们必须在训练期间将整个数据集的值保存在内存中。相反,移动平均线可以很好地代表数据的均值和方差。它更有效,因为计算是增量的——我们只需要记住最近的移动平均线。
Batch Norm 层的放置顺序
对于 Batch Norm 层应该放置在架构中的什么位置,有两种意见——激活之前和激活之后。原始论文将它放在前面,尽管我认为您会发现文献中经常提到这两个选项。有人说“之后”会产生更好的结果。
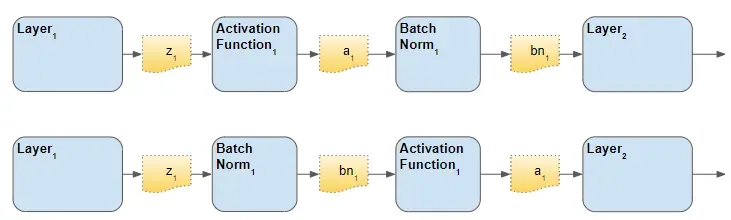
Conclusion
Batch Norm 是一个非常有用的层,您最终会在网络架构中经常使用它。希望这能让您很好地理解 Batch Norm 的工作原理。
理解为什么 Batch Norm 有助于网络训练也很有用,我将在另一篇文章中详细介绍。
最后,如果您喜欢这篇文章,您可能还会喜欢我关于变形金刚、音频深度学习和地理定位机器学习的其他系列。
让我们继续学习!
文章出处登录后可见!
