待在家里，勇敢吗？ Python 中的时间序列方法

在 COVID 爆发的前几周探索德国人的心理健康，并了解数据质量检查的重要性

只要对趋势、轨迹或季节性感兴趣，时间序列分析就是您的朋友。这一系列技术似乎在经济和金融世界（例如股票价格、营销等）中更为占主导地位，但心理学家也越来越有兴趣采用它。乍一看，这并不奇怪，因为心理过程本质上是有时间限制的，从几分钟到几年不等（例如，社会排斥后的直接痛苦或整个生命周期的认知衰退）。然而，很明显，在预测方面，人类是一个特别难以破解的难题。但是，如果我们想简单地探索随着时间推移而发生的这种心理过程的动态呢？

让我们以 COVID-19 的心理影响为例。试着回忆一下 2020 年春季有关一种新病毒传播的令人不安的消息的早期日子。除了大量尚未真正熟悉的统计数据外，媒体上还展示了载有尸体的货车和人满为患的医院。 “拉平曲线”的政治措施得到实施，并从根本上改变了我们的社会生活——几乎在一夜之间。几乎每周都会重新定义规则，公共职能几乎完全关闭。我们可以争辩说，我们一直生活在没有改善前景的紧急状态中，这种情况可能会导致抑郁症状和焦虑。因此，想知道放宽电晕措施如何减轻我们的压力以及对大流行的担忧并不牵强。 2020 年 4 月 20 日，德国发生了这样的事情：学校重新开学，并允许在 800 平方米的商店内购物。现在，这个信号如何影响公众的日常心理健康？人们真的松了一口气，“小屋热”的症状持续到五月吗？

The COVIDistress study

为了找出答案，我们将分析来自 COVIDistress 研究的数据，这是一个国际合作开放科学项目，旨在衡量全球早期新冠危机期间的经历、行为和态度。该调查包括 48 种语言，总样本量为 173,426 名参与者，他们在 2020 年 3 月 30 日至 5 月 30 日期间做出了回应。作者认为，年龄较小、作为女性、受教育程度较低、单身、与更多孩子在一起，并且生活在 COVID-19 情况更严重的国家或地区与显着更高的压力水平相关（Kowal 等人，2020 年）。由于我们是社会物种，我们天生就与其他人联系，但只是在自愿的基础上：即使与社会隔绝可能会引起孤独感，缺乏隐私同样会很痛苦。虽然承认哪些群体似乎更容易受到隔离的影响很有价值，但我想知道你是否可以追踪研究过程中感知压力的轨迹，并测试其与政治措施开始的关系。正如我们将发现的那样，这不是一件容易的事——但稍后会详细介绍。[0][1]

衡量电晕锁定的心理影响

感知压力是用 PSS-10 测量的，这是一份由 Cohen (1983) 开发的 10 项问卷，用于评估个人在上周认为生活不可预测、无法控制和超负荷的程度。为了测试人们对持续爆发的担忧程度，他们被要求评估他们对冠状病毒对不同地区（个人、本国等）的后果的担忧程度。有关确切措辞的更多详细信息，您可以在此处查看整个调查。为了让您更好地理解这些术语的实际含义，让我快速向您解释它们。[0]

一点时间序列指南

时间序列分析通常描述一个系统过程（例如，气候变化、股票价格变化等），该过程会随着时间的推移而展开，并基于等间隔的多个观察结果。

即使这不适用于我们设计更复杂的案例研究，这些多重观察实际上源于单一来源（例如，个人、索引）。一条经验法则说，您需要至少 50 次观察才能进行大致准确的预测，当然也欢迎更多数据（McCleary 等人，1980 年）。[0]

Components

时间序列数据有四种可变性来源，需要明确建模或通过数学变换（例如差分）去除以进行准确预测：

• 当中长期数据水平发生明显变化时，趋势就会出现。例如，系列开始时的数据平均值可能高于其结束时的平均值，因此呈现负趋势。
• 季节是指不断发生的增加或减少的重复模式。它可以归因于日历的各个方面（例如，月份、星期几等）。例如，我们可以观察每天早上循环上升和晚上下降的室外温度。
• 周期与季节共享一个属性：某些波动的再次发生。但与季节不同，周期没有固定的持续时间，不必归因于日历的各个方面，并且通常会在超过 2 年的时期内表现出来（例如，商业周期）。
• 随机性描述了一种不规则的变化，它使轨迹自然而无系统地抖动。它可以归因于噪声，是从数据中删除趋势、季节和周期后的剩余方差。

Concepts

自相关：另一个值得特别注意的常见方差来源称为自相关。它源于这样一种观点，即当前状态在一定程度上受到先前状态的影响。假设我在某一时刻真的很沉思，这使得我不太可能很快改变到随和的快乐模式。在心理学家的行话中，我们说先前的情感状态至少部分地决定了我们当前的情绪。然而，正如我们稍后将看到的，这个想法显然只适用于一个人的情绪，而不是个人之间的情绪，因此需要纵向数据。在统计术语中，如果变量与自身与一定数量的先前时间点（称为滞后）相关，则时间序列显示自相关。例如，2 滞后自相关是与当前值之前两次出现的值的 Pearson 相关。跨多个滞后的自相关系数称为自相关函数 (ACF)，它在模型选择和评估中发挥作用。

静止的：在现实生活中，许多时间序列不是静止的，因此轨迹呈现出摇摆不定的外观。从技术上讲，这意味着序列均值、方差和/或自相关结构确实会随着时间而变化。但是这方面使得预测任何未来值变得更加困难，因为过去的值不太相似。然而，如果我们通过数学变换（例如差分）来解释系列中存在的系统模式，我们可以实现平稳性并开始预测。

Model selection

如果预测系列中的未来点是您的主要目标，那么 ARIMA 模型可能适合您。它们是直接从数据中发展而来的，不需要关于过程可能发生的情况的理论。 ARIMA 代表自回归综合移动平均线。 AR(q) 和 MA(p) 项都指定了正式描述序列中存在的自相关的预测变量，而 I[d] 描述了已应用于使序列静止的差分顺序。

然而，我们心理学家通常实际上对系列的这些系统方面特别感兴趣。例如，我们热衷于描述第一次锁定期间感知压力变化背后的潜在趋势。或者，我们可以尝试将这些压力反应与外部因素联系起来，例如每个国家/地区新冠病毒爆发的严重程度。在另一种情况下，我们可以评估关键事件的影响，例如政治措施的变化（例如，引入口罩、有条件地重新开放商店等）。因此，除了预测之外，我们还对描述性和解释性模型感兴趣。为此，我们可以先使用回归模型，然后将 ARIMA 模型拟合到残差以解释任何剩余的自相关。如果您对更多技术细节感兴趣，您可以在 Jebb 及其同事 (2015) 的一篇论文中找到很好的解释。[0]

好的——现在让我们先检查一下我们的数据

现在我们进入有趣的部分——用 Python 编码。由于数据可以在线下载，由于 COVIDistress 开源研究项目，每个人都可以免费访问它。响应按月存储，因此我们每个月都有一个文件。要创建一个单独的文件来使用，我们需要将它们连接起来以加载一个包含所有月份的数据框。这就是如何尽可能少地准备它：设置项目路径后，我们使用列表推导来使用 Python 的 glob 库为我查找所有相关的 excel 文件。为了节省一些不必要的计算时间，我们可以将感兴趣的变量名存储在一个单独的列表中。然后我们浏览所有文件以查找相关列，并使用 pd.concat() 将它们合并到所有月份。生成的数据框可以导出到 csv 文件，因此我们只需运行一次此命令并随时返回数据。为避免反复运行脚本时出现问题，在合并所有文件之前包含一个条件：包含所有月份的 csv 文件不得已存储在我的文件夹中，否则生成的文件将包含数千个重复条目。还有一个技巧可以方便以后用 matplotlib 进行后续计算和可视化：通过告诉 pandas 根据 RecordedDate 列解析日期，日期将直接转换为 datetime64 格式，并可用作数据帧的索引。[0]

# set path
os.chdir("C:/Users/YourName/YourFolder")

# list all csv files
all_filenames = [i for i in glob.glob('*.{}'.format('csv'))]
# import only  that are relevant
cols = ['RecordedDate','Country','Dem_age','Dem_maritalstatus', 'Dem_dependents',
        'Scale_PSS10_UCLA_1', 'Scale_PSS10_UCLA_2', 'Scale_PSS10_UCLA_3', 'Scale_PSS10_UCLA_4', 
        'Scale_PSS10_UCLA_5','Scale_PSS10_UCLA_6', 'Scale_PSS10_UCLA_7','Scale_PSS10_UCLA_8',
        'Scale_PSS10_UCLA_9','Scale_PSS10_UCLA_10','Corona_concerns_1', 'Corona_concerns_2', 
        'Corona_concerns_3','Corona_concerns_4','Corona_concerns_5']

#combine all files in the list if not done yet
while 'COVIDiSTRESS All months.csv' not in all_filenames:
        df_all = pd.concat([pd.read_csv(f, encoding='latin1', usecols= cols) for f in all_filenames ])
        #export to csv
        df_all.to_csv('COVIDiSTRESS All months.csv', index=False, encoding='latin1')

df = pd.read_csv('COVIDiSTRESS All months.csv',encoding='latin1', parse_dates=['RecordedDate'], index_col='RecordedDate')

我们可以通过使用 df 上的 head() 方法看到这个数据帧的预览。通过在df上调用dtypes，我们得到每一列的数据类型。这对于验证数据是否被 pandas 正确检测到很重要。由于应对冠状病毒后果的政治措施因国家/地区而异，因此我们将重点关注德国，因此对数据进行相应的子集化。

print(df.head())
print(df.dtypes)

# select german entries
df_ger = df[df['Country']=='Germany']

坚持，稍等！我们错过了一些东西。

现在这是一个陷阱：我们有一个与纵向研究设计大不相同的特殊数据结构。尽管这项研究持续了数周，并在数周内定期对记录进行采样，但每次观察仅发生一次。这称为重复横截面设计，不能简单地在传统的 ARIMA 模型中建模，因为过去的值不能直接链接到现在或未来的值。相反，ARIMA 术语必须集成到多层次模型 (MLM) 中（Lebo 和 Weber，2014 年）。具体来说，我们可以从特定日期的所有响应中计算出平均压力水平，并将其作为人口感知压力水平的代表。但是，我们无法判断受访者第一天的压力水平与一周后的压力水平之间的关联程度，因为它是从不同的人身上采样的。[0]

此外，很明显，一个人感知到的压力不仅取决于大流行的状态，还与许多其他因素有关：一个人的压力倾向、个人问题和应对策略等等。由于没有要求相同的受访者多次评估他们的压力水平，我们没有机会将这些单独的组件与其他方差来源（例如重复测量 ANOVA 从中受益的东西）区分开来。但是，在牢记这些限制的同时，我们至少可以了解整体压力水平吗？为了确定我们是否有足够的数据来粗略估计每一天，我们计算了每一天的观察结果。事实证明，每个日期近 80% 的回复都低于 100 名参与者。相比之下，当我们查看国际样本时，只有 3% 的天数包含 100 名参与者。尽管如此，分析总样本会更加复杂，因为响应嵌套在需要分层建模的国家和日期中。

# get n per date for germany
count_per_date_ger = df_ger.index.map(lambda t: t.date()).value_counts().rename('count').sort_index()
print(count_per_date_ger)
len(count_per_date_ger[count_per_date_ger < 100])/len(count_per_date_ger)

# get n per date for all countries
count_per_date_int = df.index.map(lambda t: t.date()).value_counts().rename('count').sort_index()
print(count_per_date_int)
len(count_per_date_int[count_per_date_int < 100])/len(count_per_date_int)

# get n per month
n_per_month = df.index.strftime("%B").value_counts()
print(n_per_month)

我们可以使用一个名为 strftime 的简洁函数来获得每月观察的频率——它将日期时间索引的各个方面（例如，日、月、秒等）转换为可读性好的字符串。例如，我们可以通过在括号中使用 %B 来获取完整的月份名称（文档中的更多代码）。要查看每天对调查的响应频率如何变化，我们可以通过简单地在数据帧的索引上调用 matplotlib 的直方图函数来创建直方图——x 轴将自动格式化。[0]

import matplotlib.pyplot as plt

#  plot freq across time
plt.hist(df_ger.index,bins=61, edgecolor='k', color = 'tab:blue')
plt.axhspan(0,100, color = 'red', alpha = 0.2)
plt.xticks(rotation=60)
plt.ylabel("N of respondents")
plt.xlabel("Date")
plt.title("Frequency of responses across time", fontsize = 16)
plt.show()

免责声明：除非另有说明，否则所有图像均由作者创建。

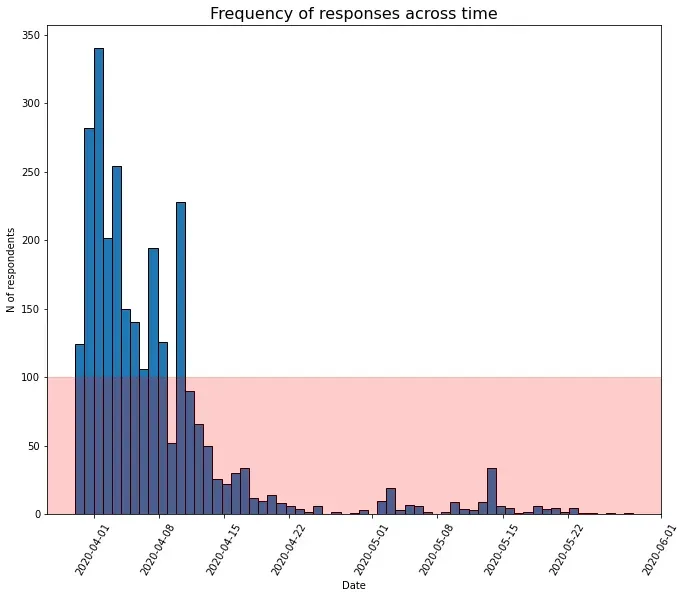
该图只是支持我们已经知道的：即使在研究期开始时大约有两周有足够的数据支持，参与的兴趣也很快消失了。

Survey results

现在，如果我们暂时将这些日常变化放在一边，德国人通常如何处理最初几个月对他们的福祉构成的威胁？

为了找出答案，我们首先创建了两个数据框，每个数据框都包含应该分别衡量感知压力和对电晕的担忧的项目的相关列。通过使用startswith()方法，我们可以很容易地找到相应尺度的所有变量，而无需繁琐的输入。接下来，我们创建两个列表以确保我们稍后在图表上放置正确的标签：

1. 每个量表的相关响应类别列表（例如，1 = 非常不同意，2 = 不同意等）和
2. 包含参与者被要求评价的陈述的列表（例如，在上周，您因意外发生的事情而感到不安的频率？，您可以在此处找到完整的调查）[0]

然后，我们构建一个函数，该函数将相应的数据子集和语句作为输入，并返回一个字典，其中包含属于规模上每个协议类别的响应百分比。通过这种方式，该函数可以很容易地应用于我们的压力和关注数据。

# assign category names
categories_stress = ['Never','Almost never', 'Sometimes', 'Fairly often', 'Very often']
categories_concerns = ['Strongly disagree', 'Disagree', 'Slightly disagree', 'Slightly agree', 'Agree', 'Strongly agree']

# replace colnames by more meaningful statements
stress_names = ['upset after unexpected event', 'unable to control life', 'nervous and stressed', 'confident to cope with own problems', 
             'things were going my way', 'not able to cope with tasks', 'able to control irritations', 'feel on top of things',
             'angry because things out of control', 'difficulties piling up']
concerns_names = ['myself', 'my family', 'my close friends', 'my country', 'other countries around the globe']

# select all columns that contain relevant responses
filter_stress_col = [col for col in df if col.startswith('Scale')]
df_stress = df_ger[filter_stress_col]
filter_concerns_col = [col for col in df if col.startswith('Corona')]
df_concerns = df_ger[filter_concerns_col]

# define a function that takes a subset of the data and column names as input to compute percentage of chosen response categories for all columns
def create_percentages(data, cols):
    results = pd.DataFrame(columns = cols)
    for col in range(0,len(data.columns)):
        this_column = results.columns[col]
        results[this_column] = data.iloc[:, col].groupby(data.iloc[:, col]).count().div(len(data)).mul(100).round().astype(int).reset_index(drop=True).to_frame() 
    return(results.to_dict('list'))

# apply
dict_stress = create_percentages(data=df_stress, cols=stress_names)
dict_concerns = create_percentages(data=df_concerns, cols=concerns_names)

这是一个示例，说明它如何从我们的德国样本中寻找感知压力量表的响应。

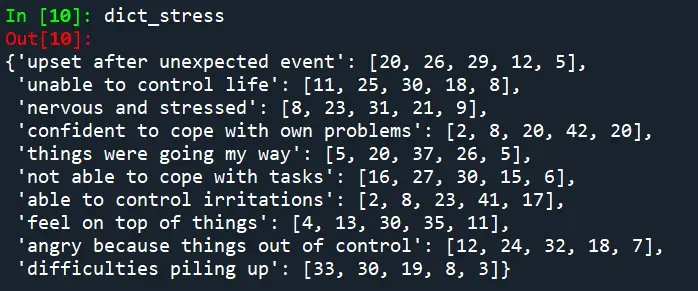
例如，事实证明，8% 的德国人最近从未感到紧张和压力，而其中 21% 的人经常感到紧张和压力。但是，我们可以通过简洁直观的数据可视化来更好地了解这些分布。不同的堆积条形图是一种很好的方式来展示受访者在多大程度上支持或拒绝特定的陈述。为此，我使用并改编了我在 Stackoverflow 上找到的代码片段（归功于 eitanlees！），根据响应类别的数量是奇数还是偶数来纠正偏移量。[0][1]

import numpy as np

# define a funtion to plot likert data as stacked divergent bar chart
def plot_likert(results, category_names, title):
    """
    Parameters
    ----------
    results : dict
        A mapping from question labels to a list of answers per category.
        It is assumed all lists contain the same number of entries and that
        it matches the length of *category_names*. The order is assumed
        to be from 'Strongly disagree' to 'Strongly aisagree'
    category_names : list of str
        The category labels.
    """
    
    labels = list(results.keys())
    data = np.array(list(results.values()))
    data_cum = data.cumsum(axis=1)
    middle_index = data.shape[1]//2
    # calculate offsets depending on whether number of response categories is even or odd
    if (len(category_names) % 2) == 0:
        offsets = data[:, range(middle_index)].sum(axis=1)  
    else: 
        offsets = data[:, range(middle_index)].sum(axis=1)  + data[:, middle_index]/2
    
    # Color Mapping
    category_colors = plt.get_cmap('coolwarm_r')(
        np.linspace(0.15, 0.85, data.shape[1]))
    
    fig, ax = plt.subplots(figsize=(10, 7))
    
    # Plot Bars
    for i, (colname, color) in enumerate(zip(category_names, category_colors)):
        widths = data[:, i]
        starts = data_cum[:, i] - widths - offsets
        ax.barh(labels, widths, left=starts, height=0.5,
                        label=colname, color=color)
    
    # Add Zero Reference Line
    ax.axvline(0, linestyle='--', color='black', alpha=.25)
    
    # X Axis
    ax.set_xlim(-90, 90)
    ax.set_xticks(np.arange(-90, 91, 10))
    ax.xaxis.set_major_formatter(lambda x, pos: str(abs(int(x))))
    
    # Y Axis
    ax.invert_yaxis()
    
    # Remove spines
    ax.spines['right'].set_visible(False)
    ax.spines['top'].set_visible(False)
    ax.spines['left'].set_visible(False)
    
    # Ledgend
    ax.legend(ncol=len(category_names), fontsize='small', 
              loc = 'upper center', bbox_to_anchor=(0.5, -0.05))
    
    # Title
    ax.set_title(title)
    
    # Set Background Color
    fig.set_facecolor('#FFFFFF')

    return fig, ax

# apply to our data
fig, ax = plot_likert(results=dict_stress, category_names=categories_stress, title='Perceived stress in Germany, spring 2020')
plt.show()
fig, ax = plot_likert(results=dict_concerns, category_names=categories_concerns, title='Concerns about the consequenses of the Corona virus in Germany, spring 2020')
plt.show()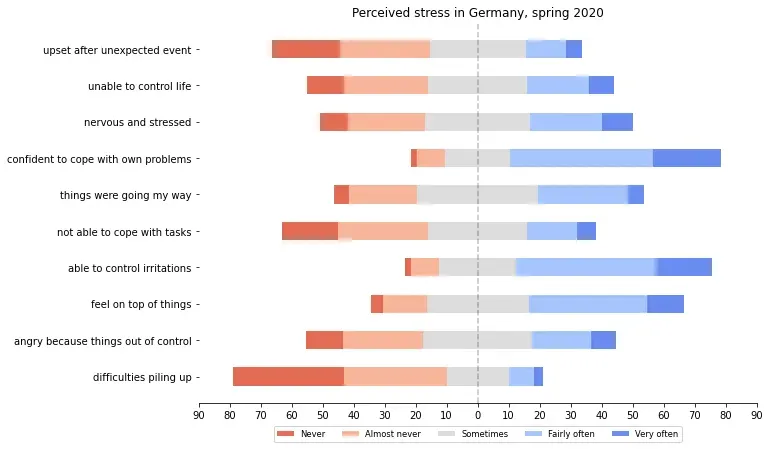

平均而言，在大流行的前几周，大多数人的精神状况都还不错——至少比例表明：积极的陈述向左转移，因此大多数参与者大部分时间都感到能够应对困难。同样，负面反应向右移动，因此大多数人只是偶尔感到对自己的生活缺乏控制。从数字上讲，只有 4% 的人从未感到过自己的事情，而 3% 的人经常遇到困难堆积如山。尽管如此，如果我们将其转换为绝对数字，则 4% 的样本（N = 2732）至少有 109 名参与者。因此，该情节并没有描绘出如此完全积极的画面，因为答案差异很大，这表明个人经历了不同程度的大流行的心理后果。此示例再次表明，值得花时间深入分析响应，而不是立即急于求平均值。

如果我们将相同的函数应用于对电晕问题的回应，就会出现一个有趣的模式……

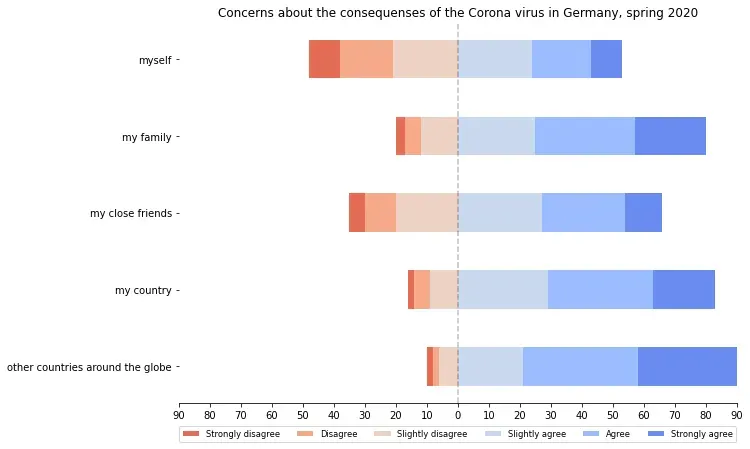
看起来人们对新冠病毒对自己和他们亲密朋友的后果的担忧不同，但大多数人都同意它对他们的国家和全球的影响。也许这归结为人们觉得即使在困难的情况下他们仍然是自己财富的建筑师。但当涉及到公众时，这种包罗万象的问题的后果不再掌握在他们手中，而是取决于更多的力量（例如，政治决策、经济发展等）。

在我们可以为所有问题创建一个反映每个人压力分数的单一分数之前，需要颠倒一些陈述。例如，如果人们高度同意“在上周，我对自己处理个人问题的能力充满信心”这一说法，这表明他们的应对能力使他们的压力感知水平保持在较低水平，这也应该反映在他们的分数中.为了实现这一点，我们可以利用字典理解来引导程序找到需要交换数字的变量。然后，我们可以在 df_stressdataframe 上使用 pandas replace() 方法，并简单地将结果字典作为参数传递。

# recode statements with reverse valence
to_recode = ['Scale_PSS10_UCLA_4', 'Scale_PSS10_UCLA_5','Scale_PSS10_UCLA_7', 'Scale_PSS10_UCLA_8']
reverse_values = {1:5, 2:4, 4:2, 5:1}
recoder_dict = {f'{x}' : reverse_values for x in to_recode}
print(recoder_dict)
df_stress_recoded = df_stress.replace(recoder_dict)

通过编写一个名为 aggregate_timeseries() 的函数，该函数包括以下步骤：我们逐行汇总每个语句的所有分数，即针对每个单独的观察。因为仅此操作的结果对象将是一个没有指定名称的系列，所以我们将其转换为数据框并修复命名问题。即使这个分数包含我们想要的——一个反映每个人感知压力的综合分数——我们甚至可以将它分解为每个人每天一个分数，这种技术被广泛称为下采样。对于这项任务，我们可以使用重采样方法来获取一天内所有观察值的平均值。研究期间可能还包括我们没有任何数据的一天，因此我们可以使用 interpolate() 来估算当天可能的压力分数。经过一些格式化后，我们的 daily_timeseries() 函数可以获取包含每次观察一个分数的任何数据帧，并将其转换为每日平均值的时间序列。

# aggregate time series data for plotting
def aggregate_timeseries(dataframe,name):
    sum_scores = dataframe.mean(axis = 1)
    sum_df = sum_scores.to_frame().rename(columns = {0:name})
    return(sum_df)

stress_M = aggregate_timeseries(df_stress_recoded, 'Stress')
concerns_M = aggregate_timeseries(df_concerns, 'Concerns')

def daily_timeseries(dataframe, name):
    df_daily = dataframe.resample('D').agg('mean').interpolate()
    df_daily.columns = [name +"_M"]
    return(df_daily)

# downsample to daily
df_stress_daily = daily_timeseries(stress_M, 'Stress')
df_concerns_daily = daily_timeseries(concerns_M, 'Concerns')

现在，整体压力评分如何随时间变化？日常数据的可用性如何影响最终的轨迹？让我们可视化两个数据点所代表的分数的可变性以及每日平均值。首先，我们需要通过合并各自的数据框来组合压力和关注响应。为了标注德国放松措施的日期（2020 年 4 月 20 日），我们将 datetime 导入为 dt，以包含与 datetime 索引兼容的格式的垂直虚线。此外，我们通过将 alpha 设置为 0.1 来增加单个点的不透明度来处理可能重叠的数据点。

import datetime as dt
import matplotlib.dates as mdates

# merge daily stress and concern data
df_combined = df_concerns_daily.join(df_stress_daily)

# set subplot canvas and share x axis(dates) 
fig, ax = plt.subplots(2,1, figsize=(10, 10),sharex=True)

# plot daily averages
ax[0].plot(df_combined.index, df_combined['Stress_M'], color = 'tab:blue', linewidth = 2)
# plot individual stress scores
ax[0].scatter(stress_M.index, stress_M['Stress'], color = 'grey', alpha = 0.1)
# annotate relaxations
ax[0].axvline(dt.datetime(2020, 4, 20),color = 'grey', linestyle = '--')
# format x and y axis ticks
ax[0].set_yticks(np.arange(0, 5, step=1))
ax[0].set_xticks(pd.date_range(dt.datetime(2020, 4, 20), periods = 7))
# show date label every wednesday
ax[0].xaxis.set_major_locator(mdates.WeekdayLocator(interval=1))
# set custom date format
ax[0].xaxis.set_major_formatter(mdates.DateFormatter('%d-%m-%Y'))
# set axis labels
ax[0].set_ylabel("Composite score")
# set subplot title
ax[0].title.set_text('Perceived Stress')

# plot daily averages
ax[1].plot(df_combined.index, df_combined['Concerns_M'], color = 'tab:orange', linewidth = 2)
# plot individual concerns scores
ax[1].scatter(concerns_M.index, concerns_M['Concerns'], color = 'grey', alpha = 0.2)
# annotate relaxations
ax[1].axvline(dt.datetime(2020, 4, 20),color = 'grey', linestyle = '--')
# rotate x axis labels (dates)
ax[1].xaxis.set_tick_params(rotation=45)
# set axis labels
ax[1].set_xlabel("Date")
ax[1].set_ylabel("Composite score")
# set subplot title
ax[1].title.set_text('Concerns about Corona')

# set main title and show
fig.suptitle("Reported mental health during the early outbreak of COVID in germany", fontsize = 20)
plt.show()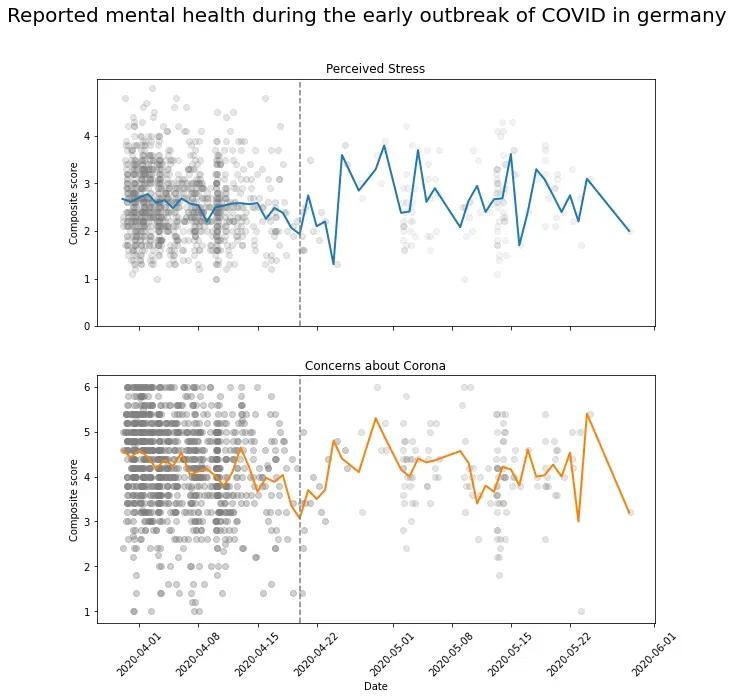

现在很明显这里发生了什么。灰色散点的密度越高，我们对这个特定时间点的数据就越多。因此，在研究的第一阶段，日平均值得到了大致足够的数据支持。似乎平均压力估计值有所下降。当谈到对电晕的担忧时，这似乎更加明显，但这归结为一个简单的技术事实：规模更窄，这样斜率（例如，从时间 A 到时间 B）比如果规模更广。

在研究期间的剩余时间里，每日平均值基于很少的数据，因为这些点像五彩纸屑一样分散。在某一天，它甚至是根据一次观察计算的（使用平均冗余）。因此，这条线在较高值和较低值之间波动很大，具体取决于样本的响应。看——这很好地展示了我们通常使用算术平均值来表示小样本中的平均值的问题：它对极端的个体值非常敏感。因此，我们在这里看到的轨迹不是随着时间的推移在德国人口中感知压力的发展，而是很可能是噪音。因此，我们可以拒绝将数据用于更复杂的时间序列建模的想法，因为我们遇到了轨迹完全随机的可能性：每天，都会抽取一个新的子样本来计算应该代表的平均值民众的心理状态与前一天一样。这就像将苹果与橙子进行比较，但仍试图找到它们之间的联系。

首先对您的数据进行数据科学

不要因为无法运行“实际”分析而感到失望——它只会给我们带来无法解释的、实际上没有意义的结果。这也是由于探索性分析的性质：如果数据集不适合分析，则无法使其适合。因此，我们无法回答电晕的放松在多大程度上对公众所经历的压力产生了影响的问题。但是除了时间序列分析的所有术语之外，我们还学到了很多关于检查数据适用性的重要性。最终，仅靠统计数据无法得出有意义的事实。只有分析师会。

References

[1] A. Lieberoth、J. Rasmussen、S. Stoeckli、T. Tran、D.B. Ćepulić、H. Han、S. Y. Lin、J. Tuominen、G. A. Travaglino 和 S. Vestergren，COVIDiSTRESS 全球调查网络，（2020 年）。 COVIDiSTRESS 全球调查。 DOI 10.17605/OSF.IO/Z39US，取自 osf.io/z39us[0]

[2] M. Kowal, T. Coll‐Martín, G. Ikizer, J. Rasmussen, K. Eichel, A. Studzińska, … & O. Ahmed，在 COVID‐19 大流行期间谁的压力最大？来自26个国家和地区的数据。 (2020)，应用心理学：健康与幸福，12(4), 946–966[0]

[3] R. McCleary、R. A. Hay、E. E. Meidinger 和 D. McDowall，《社会科学应用时间序列分析》（1980 年），Sage Publications[0]

[4] A. T. Jebb, L. Tay, W. Wang & Q. Huang，心理学研究的时间序列分析：检查和预测变化（2015），心理学前沿，6, 727[0]

[5] M. J. Lebo & C. Weber, 重复横截面设计的有效方法 (2015), 美国政治学杂志, 59(1), 242–258[0]