摘要
本周从NLP方向,详细理解了Transformer的词向量,位置编码,编码器的子注意力的mask原理,与Decoder原理精讲,特别是对mask 的处理逻辑的实现与pytorch逐行实现;从更底层的六大细节去理解Transformer的原理与实现,可以更好的方便日后的工作需求。
参考:
1. Transformer的理解与代码实现—Autoformer文献阅读:是从整体到局部的实现思路,分为三个部分:编码层,解码层,输出层。
2.Transformer结构解析(附源代码)
一. 细致理解Transforemr模型Encoder原理讲解与其Pytorch逐行实现
本章的难点讲解:如图
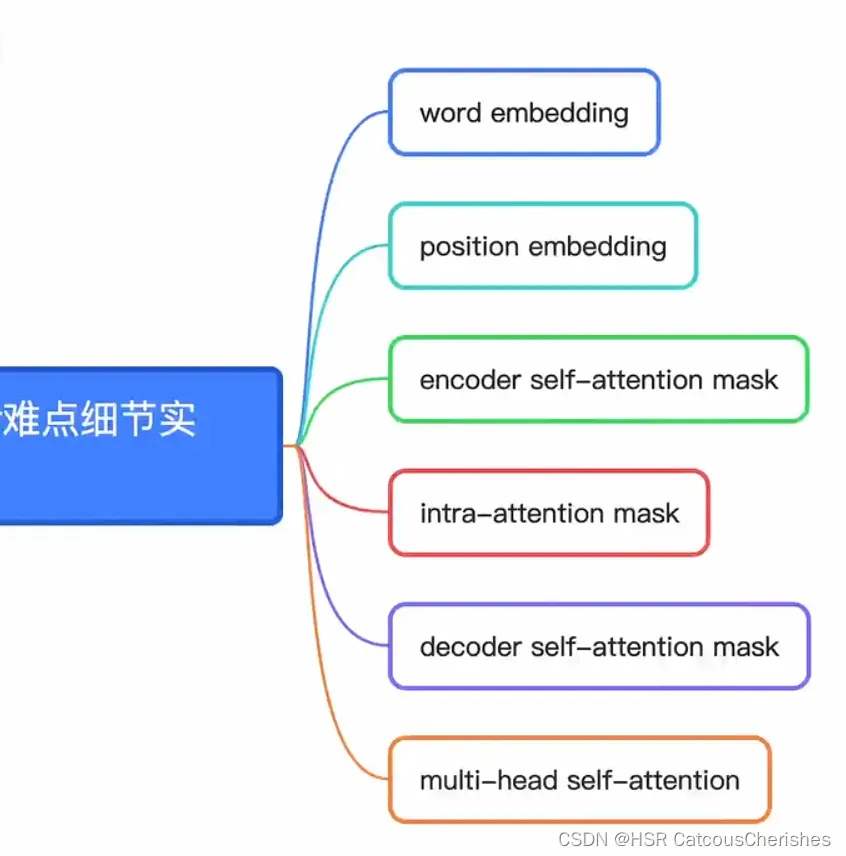
1.1 关于word embedding
word embedding是以序列建模的,假设是离散型的,考虑source,target sentence。
input_src:输入句子有两个,第一个长度为2,第二个长度为4
input_tgt: 目标句子有两个。第一个长度为4, 第二个长度为3
import torch
import numpy
import torch.nn as nn
import torch.nn.functional as F
# 关于word embedding,是以序列建模的,假设是离散型的,考虑source,target sentence.
# 构建序列,序列的字符以其在词表中的索引形式表示
batch_size = 2
# 单词表数目大小
max_num_src_words = 8
max_num_tgt_words = 8
# feature 假定为8,特意放小一点
model_dim = 8
max_position_len = 5
# src_len = torch.randint(2,5,(batch_size,))
# tgt_len = torch.randint(2,5,(batch_size,))
# 输入句子有两个,第一个长度为2,第二个长度为4
src_len = torch.Tensor([2,4]).to(torch.int32)
# 目标句子有两个。第一个长度为4, 第二个长度为3
tgt_len = torch.Tensor([4,3]).to(torch.int32)
1.2 生成源句子与目标句子
Step1. 根据单词索引序列,构成了源句子与目标句子,构建了batch ,并且做了padding ,默认值为0
用随机数生成句子单词索引,用0填充空白位置,保持所有句子长度一致!
# 用随机数生成句子单词索引,用0填充空白位置,保持所有句子长度一致!
src_seq = torch.cat([torch.unsqueeze(F.pad(torch.randint(1, max_num_src_words, (L, )), (0, max(src_len)-L)), 0) \
for L in src_len])
tgt_seq = torch.cat([torch.unsqueeze(F.pad(torch.randint(1, max_num_tgt_words, (L, )), (0, max(tgt_len)-L)), 0) \
for L in tgt_len])
print(src_seq)
print(tgt_seq)
输出句子索引序列:
tensor([[4, 7, 0, 0],
[4, 5, 5, 3]])
tensor([[7, 1, 6, 2],
[7, 3, 5, 0]])
Step2 . 构建word embedding,做embedding 需要把第0行留给padding
src_embedding_table = nn.Embedding(max_num_src_words+1, model_dim)
tgt_embedding_table = nn.Embedding(max_num_tgt_words+1, model_dim)
# 输入单词的字典
# print(src_embedding_table.weight)
# 目标单词的字典
# print(tgt_embedding_table.weight)
实际上在做NLP实际案列中,首先将原始文本变成一个个数字,就是每个单词在词典中所在的位置,第0个位置留给padding;再构建batch,embedding。
最后: 通过构建的词表embedding,再利用索引,得到向量化的句子
src_embedding = src_embedding_table(src_seq)
tgt_embedding = tgt_embedding_table(tgt_seq)
print(src_embedding)
print(tgt_embedding)
输出src_embedding与tgt_embedding:
tensor([[[ 0.6325, 0.6740, 0.6231, -0.1018, -0.5694, -1.1284, -0.8267,
-0.3513],
[ 0.6325, 0.6740, 0.6231, -0.1018, -0.5694, -1.1284, -0.8267,
-0.3513],
[ 0.8624, 0.1538, 0.7260, 0.9553, -0.3343, -0.4233, 0.8381,
-2.3157],
[ 0.8624, 0.1538, 0.7260, 0.9553, -0.3343, -0.4233, 0.8381,
-2.3157]],
[[-1.0009, -1.0215, -0.8428, 0.3813, -1.4925, 0.9971, -0.3106,
-1.7358],
[-0.9339, -0.1864, 1.2338, -0.4701, 0.4488, -0.5088, -1.1544,
-0.5854],
[-0.9339, -0.1864, 1.2338, -0.4701, 0.4488, -0.5088, -1.1544,
-0.5854],
[ 0.6325, 0.6740, 0.6231, -0.1018, -0.5694, -1.1284, -0.8267,
-0.3513]]], grad_fn=<EmbeddingBackward>)
tensor([[[ 0.0907, 0.1538, -0.5609, 0.7355, -0.2392, 0.5607, -0.2989,
0.6386],
[-0.2731, -0.5574, -0.1795, -0.1582, -1.6450, -0.3819, 1.6671,
-1.1886],
[-0.1661, 0.7636, 1.3906, 0.1128, -1.5198, 0.3036, 1.4455,
0.1572],
[-0.6655, 0.7795, -1.6390, -0.7333, -0.2438, -1.5009, 0.8396,
0.0397]],
[[ 0.0907, 0.1538, -0.5609, 0.7355, -0.2392, 0.5607, -0.2989,
0.6386],
[ 0.9494, -0.1407, 0.7661, 0.4011, -0.5790, 0.3481, 0.2611,
0.2383],
[-1.3839, 1.2739, -0.7151, -0.1176, -2.0195, 2.1775, 1.7719,
-3.8777],
[-0.8986, 1.7846, 0.1736, -0.0631, -0.9591, 2.6482, 1.5589,
-0.2583]]], grad_fn=<EmbeddingBackward>)
1.3 构建postion embedding
根据原始论文公式:
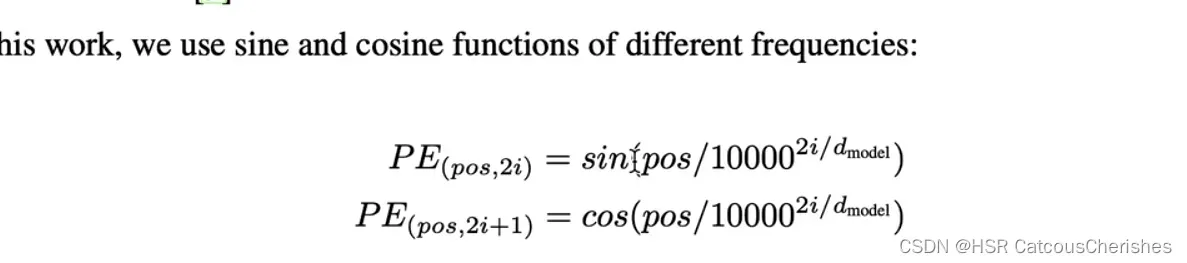
构建postion embedding 根据原始论文中的公式!!!,得到分子pos的值,pos代表行,(i代表列,特征维度的变化)
pos_mat = torch.arange(max_position_len).reshape((-1, 1))
# 得到分母值
i_mat = torch.pow(10000, torch.arange(0, 8, 2).reshape((1, -1))/8)
print(pos_mat)
print(i_mat)
# 初始化位置编码矩阵
pe_embedding_table = torch.zeros(max_position_len, model_dim)
# 得到偶数列位置编码
pe_embedding_table[:, 0::2] =torch.sin(pos_mat / i_mat)
# 得到奇数列位置编码
pe_embedding_table[:, 1::2] =torch.cos(pos_mat / i_mat)
# print(pe_embedding_table)
pe_embedding = nn.Embedding(max_position_len, model_dim)
# 设置位置编码不可更新参数
pe_embedding.weight = nn.Parameter(pe_embedding_table, requires_grad=False)
# print(src_seq,tgt_seq)
# print(pe_embedding.weight)
构建位置索引
scr_pos = torch.cat([torch.unsqueeze(torch.arange(max(src_len)),0) for _ in src_len]).to(torch.int32)
tgt_pos = torch.cat([torch.unsqueeze(torch.arange(max(tgt_len)),0) for _ in tgt_len]).to(torch.int32)
构建位置编码的思路,是借助nn.Embedding 这个API,通过 位置索引,直接得到位置embedding。
# 构建位置编码的思路,是借助nn.Embedding 这个API,通过 位置索引,直接得到位置embedding
scr_pe_embedding = pe_embedding(scr_pos)
tgt_pe_embedding = pe_embedding(tgt_pos)
print(scr_pe_embedding)
print(tgt_pe_embedding)
输出scr_pe_embedding 源句子位置编码:
tensor([[[ 0.0000e+00, 1.0000e+00, 0.0000e+00, 1.0000e+00, 0.0000e+00,
1.0000e+00, 0.0000e+00, 1.0000e+00],
[ 8.4147e-01, 5.4030e-01, 9.9833e-02, 9.9500e-01, 9.9998e-03,
9.9995e-01, 1.0000e-03, 1.0000e+00],
[ 9.0930e-01, -4.1615e-01, 1.9867e-01, 9.8007e-01, 1.9999e-02,
9.9980e-01, 2.0000e-03, 1.0000e+00],
[ 1.4112e-01, -9.8999e-01, 2.9552e-01, 9.5534e-01, 2.9995e-02,
9.9955e-01, 3.0000e-03, 1.0000e+00]],
[[ 0.0000e+00, 1.0000e+00, 0.0000e+00, 1.0000e+00, 0.0000e+00,
1.0000e+00, 0.0000e+00, 1.0000e+00],
[ 8.4147e-01, 5.4030e-01, 9.9833e-02, 9.9500e-01, 9.9998e-03,
9.9995e-01, 1.0000e-03, 1.0000e+00],
[ 9.0930e-01, -4.1615e-01, 1.9867e-01, 9.8007e-01, 1.9999e-02,
9.9980e-01, 2.0000e-03, 1.0000e+00],
[ 1.4112e-01, -9.8999e-01, 2.9552e-01, 9.5534e-01, 2.9995e-02,
9.9955e-01, 3.0000e-03, 1.0000e+00]]])
1.4 构建encoder 的self-attention mask
由于句子长度不一,我们通常需要padding 0 填充,为消除其对训练的影响,便可以用 mask。
Mask机制几乎贯穿了Transformer架构的始终,若不能首先将mask机制交代清楚,就难以对Transformer进行连贯的阐述。padding mask是由NLP这类特定任务带来的,NLP的特点为“不同的输入语句可能是不定长的”。
注意: 这里的mask不是因果关系的,不是对目标序列的那个mask ,只是对填充的部分进行mask,使其不能影响训练过程!
# mask shape : [batch_size,max_src_len,max_src_len]
# 得到有效位置矩阵,先根据src_len,构建有效矩阵,padding 0 填充
vaild_encoder_pos = torch.unsqueeze(torch.cat([torch.unsqueeze(F.pad(torch.ones(L), (0, max(src_len) - L)), 0)\
for L in src_len]), 2)
# print(vaild_encoder_pos)
valid_encoder_pos_matrix = torch.bmm(vaild_encoder_pos, vaild_encoder_pos.transpose(1, 2)) # 两个矩阵相乘,乘于本身的转置,得到有效矩阵
print(valid_encoder_pos_matrix)
输出:valid_encoder_pos_matrix
tensor([[[1., 1., 0., 0.],
[1., 1., 0., 0.],
[0., 0., 0., 0.],
[0., 0., 0., 0.]],
[[1., 1., 1., 1.],
[1., 1., 1., 1.],
[1., 1., 1., 1.],
[1., 1., 1., 1.]]])
得到无效矩阵
我们利用对有效矩阵取反
invalid_encoder_pos_matrix = 1-valid_encoder_pos_matrix
mask_encoder_self_attention = invalid_encoder_pos_matrix.to(torch.bool)
print(mask_encoder_self_attention)
输出:padding 0 位置为 True
tensor([[[False, False, True, True],
[False, False, True, True],
[ True, True, True, True],
[ True, True, True, True]],
[[False, False, False, False],
[False, False, False, False],
[False, False, False, False],
[False, False, False, False]]])
得到mask矩阵
# 初始化mask矩阵,对Key和query都做mask!!
score = torch.randn(2, max(src_len), max(src_len))
# 用极小数填充
mask_score = score.masked_fill(mask_encoder_self_attention, -1e9)
# 再softmax一下
mask_score_softmax = F.softmax(mask_score,-1)
print(src_len)
print(score)
print(mask_score)
print(mask_score_softmax)
输出:
tensor([2, 4], dtype=torch.int32)
tensor([[[-2.0870, 1.3895, 1.9857, -0.2621],
[-0.5217, -0.2295, -1.2350, 0.6592],
[-0.9797, -0.4004, -0.1669, -0.9826],
[ 0.9760, 0.1565, 0.0362, -0.3527]],
[[ 0.9125, 0.2363, -0.3818, -1.0082],
[-0.4920, -0.1994, -0.4127, 0.4671],
[-0.5775, -0.6453, 0.5197, 0.5198],
[-1.0439, 0.3213, -1.7031, -0.8907]]])
tensor([[[-2.0870e+00, 1.3895e+00, -1.0000e+09, -1.0000e+09],
[-5.2175e-01, -2.2950e-01, -1.0000e+09, -1.0000e+09],
[-1.0000e+09, -1.0000e+09, -1.0000e+09, -1.0000e+09],
[-1.0000e+09, -1.0000e+09, -1.0000e+09, -1.0000e+09]],
[[ 9.1253e-01, 2.3628e-01, -3.8176e-01, -1.0082e+00],
[-4.9205e-01, -1.9945e-01, -4.1273e-01, 4.6709e-01],
[-5.7750e-01, -6.4531e-01, 5.1966e-01, 5.1979e-01],
[-1.0439e+00, 3.2128e-01, -1.7031e+00, -8.9073e-01]]])
tensor([[[0.0300, 0.9700, 0.0000, 0.0000],
[0.4275, 0.5725, 0.0000, 0.0000],
[0.2500, 0.2500, 0.2500, 0.2500],
[0.2500, 0.2500, 0.2500, 0.2500]],
[[0.5184, 0.2636, 0.1421, 0.0759],
[0.1658, 0.2221, 0.1795, 0.4326],
[0.1262, 0.1179, 0.3779, 0.3780],
[0.1515, 0.5935, 0.0784, 0.1766]]])
二. Decoder原理精讲与pytorch逐行实现
2.1 构建 intra_attention 的mask(交叉attention)
# Q @ K^T shape [batch_size,tgt_len,src_len]
vaild_encoder_pos = torch.unsqueeze(torch.cat([torch.unsqueeze(F.pad(torch.ones(L), (0, max(src_len) - L)), 0)\
for L in src_len]), 2)
vaild_decoder_pos = torch.unsqueeze(torch.cat([torch.unsqueeze(F.pad(torch.ones(L), (0, max(tgt_len) - L)), 0)\
for L in tgt_len]), 2)
# 得到有效交叉注意矩阵
valid_cross_pos_matrix = torch.bmm(vaild_decoder_pos,vaild_encoder_pos.transpose(1,2))
print(vaild_encoder_pos)
print(vaild_decoder_pos)
print(valid_cross_pos_matrix)
invalid_cross_pos_matrix = 1-valid_cross_pos_matrix
mask_cross_attention = invalid_cross_pos_matrix.to(torch.bool)
print(mask_cross_attention)
score1 = torch.randn(2, max(tgt_len), max(src_len))
mask_score1 = score1.masked_fill(mask_cross_attention, -1e9)
mask_score_softmax1 = F.softmax(mask_score1,-1)
print(score1)
print(mask_score1)
print(mask_score_softmax1)
注意:valid_cross_pos_matrix,有效交叉注意矩阵是decoder Q 与encoder K ^T 的相关有效性!!!
2.2 构建decoder self-attention mask(真值mask)
vaild_decoder_tri_matrix = torch.cat([torch.unsqueeze(F.pad(torch.tril(torch.ones((L,L))),(0,max(tgt_len)-L,0,max(tgt_len)-L)),0)\
for L in tgt_len])
print(vaild_decoder_tri_matrix)
输出三角矩阵:
tensor([[[1., 0., 0., 0.],
[1., 1., 0., 0.],
[1., 1., 1., 0.],
[1., 1., 1., 1.]],
[[1., 0., 0., 0.],
[1., 1., 0., 0.],
[1., 1., 1., 0.],
[0., 0., 0., 0.]]])
# [1., 0., 0., 0.] 意思是 第一次解码时,样本1只注意到第一个单词;
#[1., 1., 0., 0.] 意思是 第二次解码时,样本1只注意到前两个单词;
#[1., 1., 1., 0.] 同理
构建无效矩阵,再做mask ,再softmax
invalid_decoder_tri_matrix = 1-vaild_decoder_tri_matrix
invalid_decoder_tri_matrix_attention = invalid_decoder_tri_matrix.to(torch.bool)
score2 = torch.randn(batch_size,max(tgt_len),max(tgt_len))
mask_score2 = score2.masked_fill(invalid_decoder_tri_matrix_attention, -1e9)
mask_score_softmax2 = F.softmax(mask_score2,-1)
print(tgt_len)
print(mask_score_softmax2)
输出因果mask :
tensor([4, 3], dtype=torch.int32)
tensor([[[1.0000, 0.0000, 0.0000, 0.0000],
[0.8917, 0.1083, 0.0000, 0.0000],
[0.3448, 0.6326, 0.0225, 0.0000],
[0.3430, 0.0674, 0.3615, 0.2281]],
[[1.0000, 0.0000, 0.0000, 0.0000],
[0.9143, 0.0857, 0.0000, 0.0000],
[0.4855, 0.1966, 0.3179, 0.0000],
[0.2500, 0.2500, 0.2500, 0.2500]]])
“防止解码器看到未来真值”的目的。
2.3 构建scaled self attention
在尺度点乘注意力中,通过除d_k对相关矩阵中的数值进行尺度变换,防止个别值过大而进入softmax函数的饱和区,使得softmax后的注意力值集中分布在0附近或1附近。
def scale_dot_product_attention(Q,K,V,attn_mask):
score = torch.bmm(Q,K.transpose(-2,-1))/torch.sqrt(model_dim)
masked_score = score.masked_fill(attn_mask,-1e9)
prob_attention = F.softmax(masked_score,-1)
context = torch.bmm(prob_attention,V)
return context
总结
一是Transformer中的mask机制可以分为两类,即”padding mask”与”真值mask”,其作用各不相同。理解好mask机制对模型来说是有必要的。
二是
文章出处登录后可见!
