https://speech.ee.ntu.edu.tw/~hylee/ml/2021-spring.php
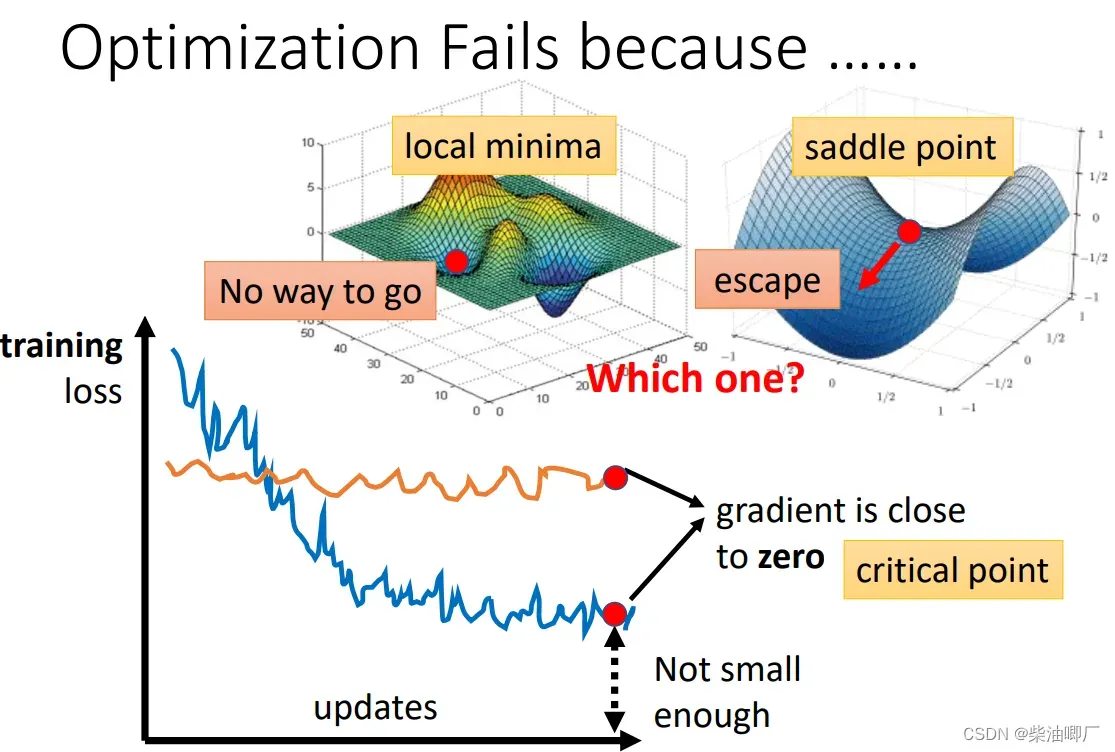
1. local minima and saddle point 局部最优和鞍点
https://speech.ee.ntu.edu.tw/~hylee/ml/ml2021-course-data/small-gradient-v7.pdf
local minima: 微分为零
saddle point: critical point 微分为零
根据泰勒展开公式,一次求导为0后可以看二次求导,判断是saddle point or local minima point.
如果红色二次求导部分恒大于0,则L(theta) > L(theta ‘) 恒成立,处于local minima。
如果红色二次求导部分恒小于0,则L(theta) < L(theta ‘) 恒成立,处于local maxima。
如果红色二次求导部分有时大于有时小于0,则处于saddle point。

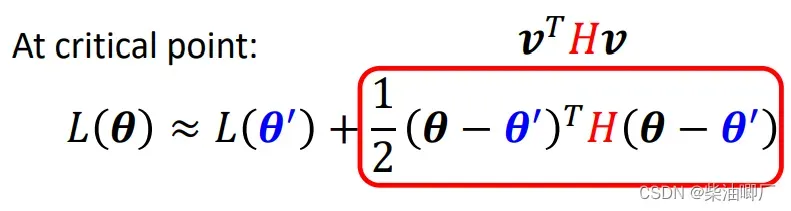
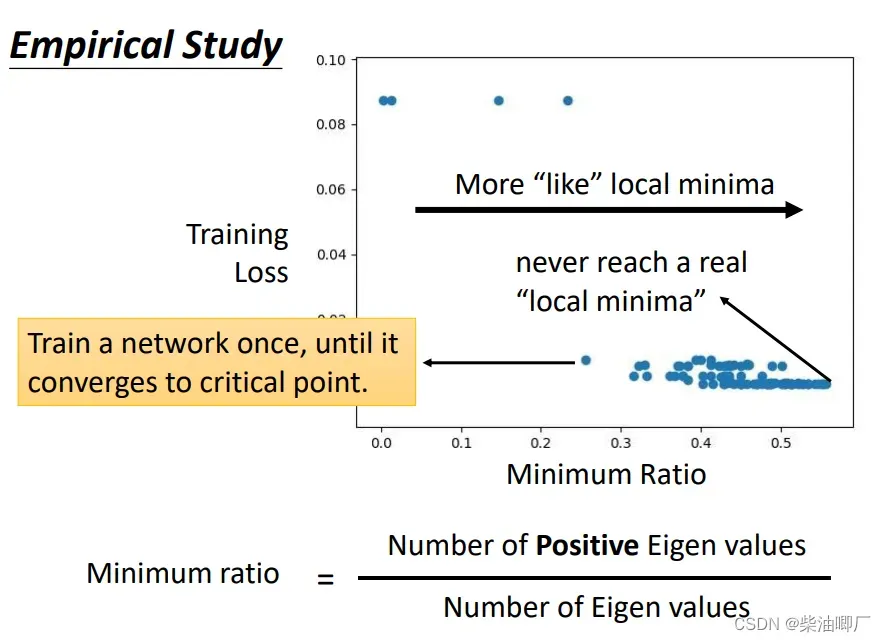
当碰到saddle point 的时候,是可以通过特征向量/特征值判断方向的。
实际应用中已经很少用算特征值的方法了,因为当参数很多的时候,这种方法会运算量巨大。

当在一维的图中看上去是local minima, 在二维时看上去就是saddle point了.在实际训练时可能会有几十上百的参数,非常多维的。即使在训练非常好的时候,特征值也不一定全都是正的,也就是说都不是处于local minima, 而是在saddle point.
2. Batch and momentum 批次与动量
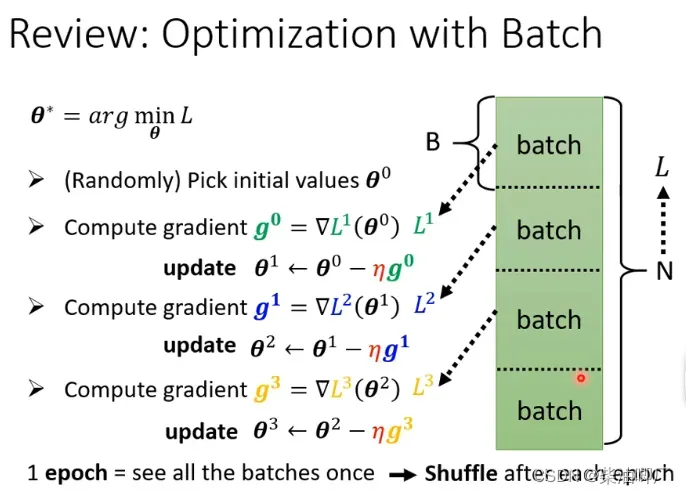
Batch
将数据集分为多个batch, 每一个batch都会算一次gradient更新参数。
重新打乱,再分一次batch(批次),每次这个动作就称为一个epoch(轮次).
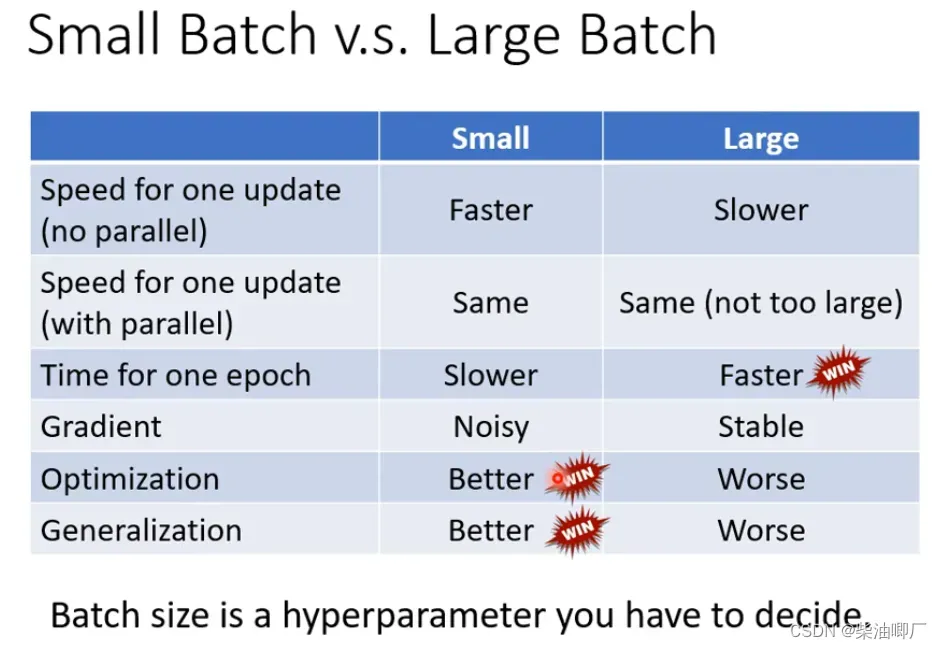
large batch size(e.g. 20 个样本都在一个btach)批次计算, 更新一次需要遍历所有example, 历时长,但是很有效。
small batch size (e.g. 每个batch只有一个样本), 更新一次只需要遍历一个example, 每次更新的时间短, 但是不稳定。
但如果在平行运算中,两者的时间是差不多的。

总结比较:两者优势相平衡,找到合适的batchsize, 这个就是要调的超参数。
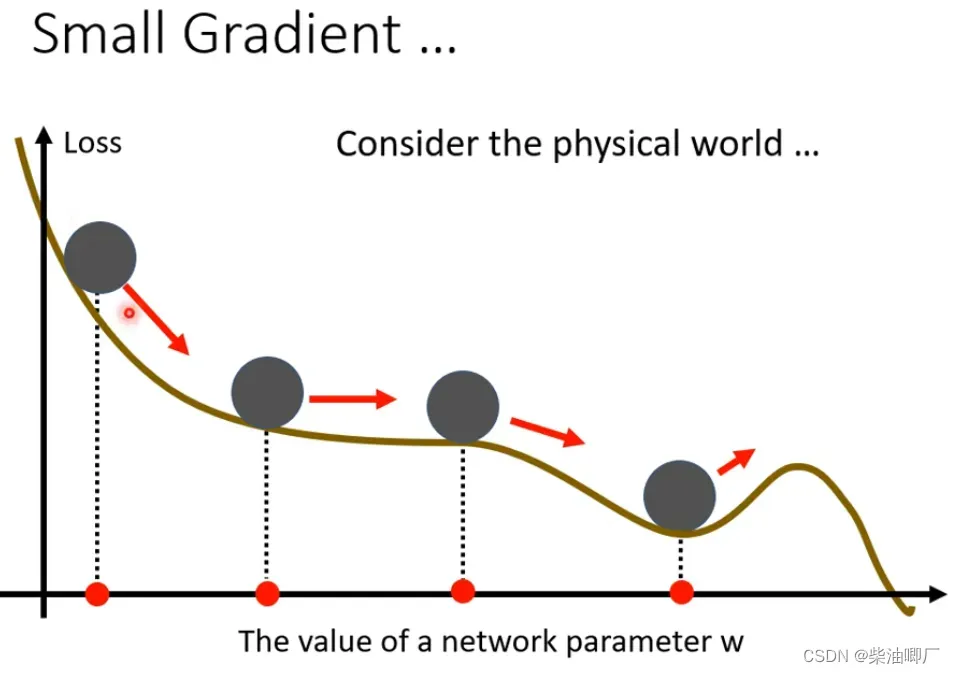
Momentum
在物理世界里,如果小球从error surface 上滚下来,到达local minima的时候,如果此时动能够大,它并不会停下来,有可能会继续往前,绕过local minima前往下一个滑坡。
所以这个方法中,不仅仅要考虑gradient的反方向,还要考虑前一步移动的方向(动能),来决定下一步移动的方向。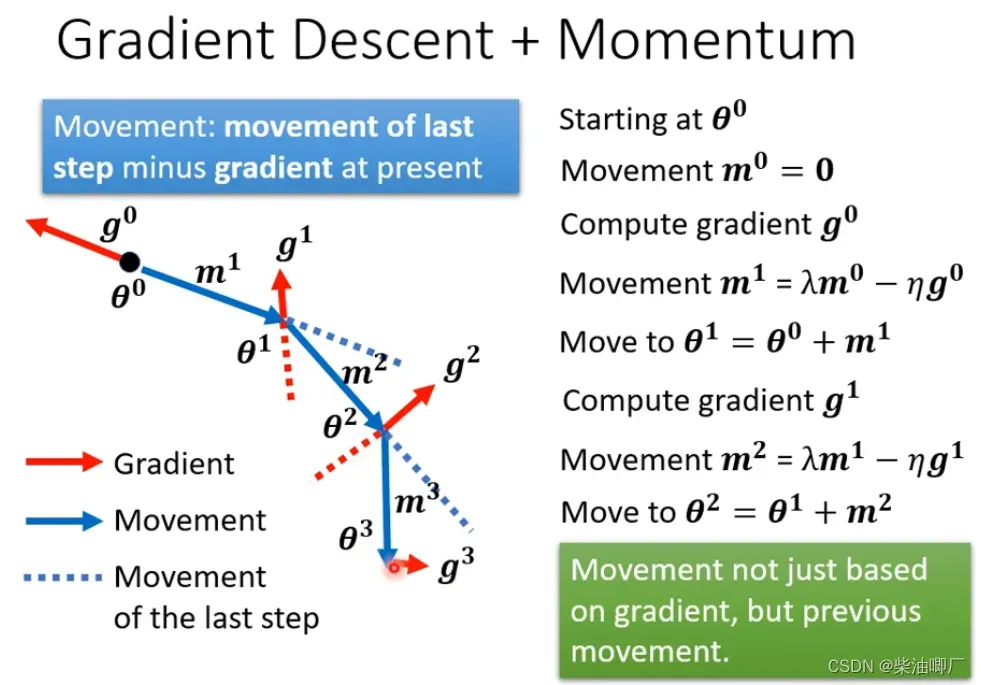
对于每次加上的momentum mi, 另一种解读可以是过去所有momentum 加上权重的结果
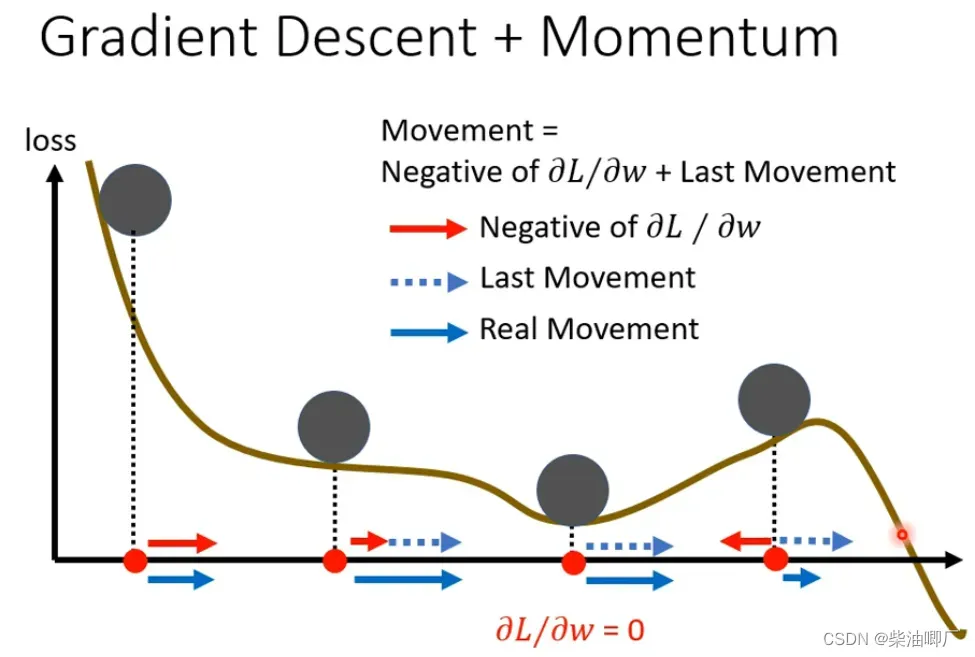
假设已经到达了local minimu, 此时gradient 是0, 但由于有momentum, 还会继续向前, 甚至当gradient是负数时,如果momentum足够大,还会继续向前进一步。
关于local minima/saddle point 以及解决办法的总结:

3. Adaptive Learning Rate
https://speech.ee.ntu.edu.tw/~hylee/ml/ml2021-course-data/optimizer_v4.pdf
在很多情况下,loss已经不发生变化了,但是gradient还是会变大,这不是因为到达了local minima or saddle point, 而是有其他的状况。比如在local minima上方来回跳跃。
即使没有local/saddle, training还是会非常困难。
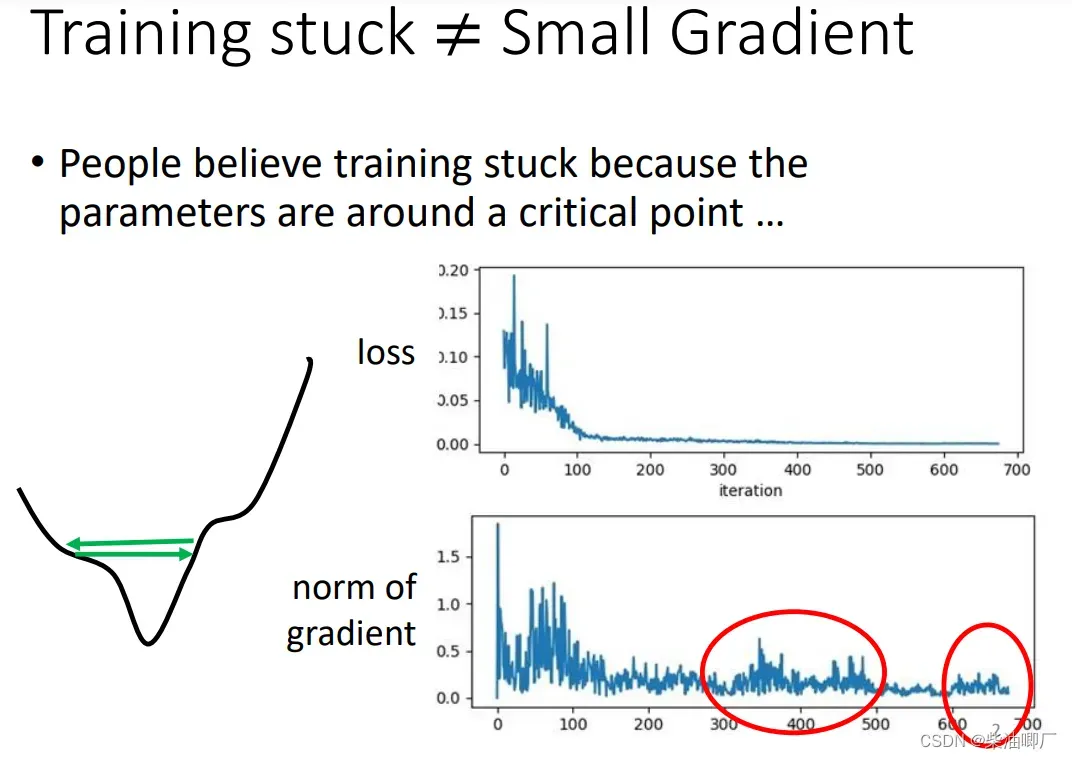
Learning rate 太大,会在最低点上方来回震荡;Learning rate 太小,经过无数次更新参数,都很难到达最低点。
learning rate 除以另一个变量sigma来进行调整,这个变量和parameter/iteration都有关,每一个参数的每一次迭代都会对应一个变量来调整学习率。
我们希望在比较平缓的地方,即gradient小时,learning rate更大;在比较陡峭的地方,即gradient大时,learning rate比较小。sigma的设计最好能满足这样的条件。
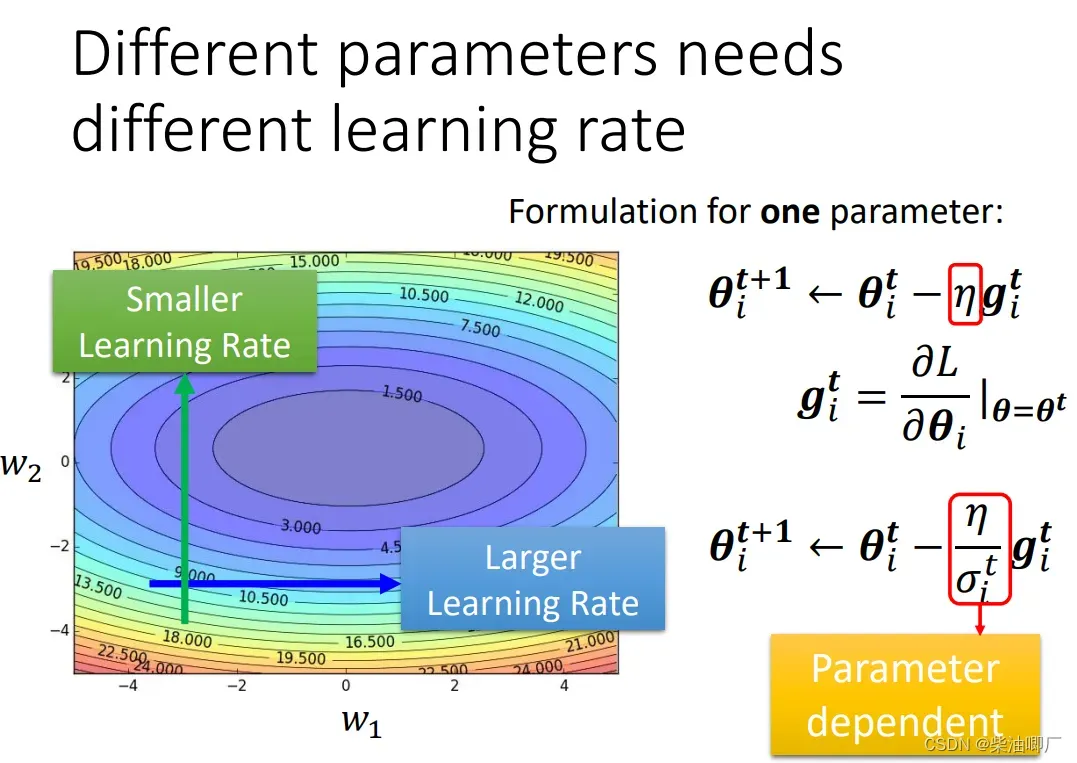
sigma 的设计有多种:
1. Root Mean Square (used in Adagrad)
第一种是 sigma 为过去所有迭代Gradient的root mean sqaure。 以一个参数为例。
这种方法中,由于sigma在分母,就能得到gradient大,调整后learningrate 小,反之一样,的效果。
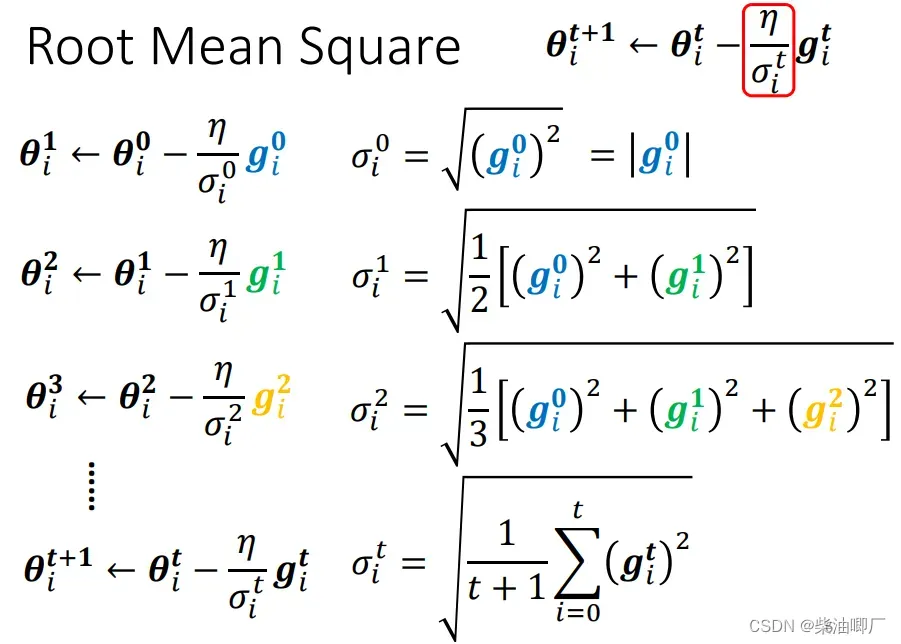
2. RMSProp
第二种方法是RMSProp. 过去的sigma平方和会与现在的grandient有一个比例系数afa. 如果afa接近与0,则认为当前的gradient的值比较重要,接近1就更倾向于考虑之前的gradient值。这里afa也是一个超参数需要人为调试。
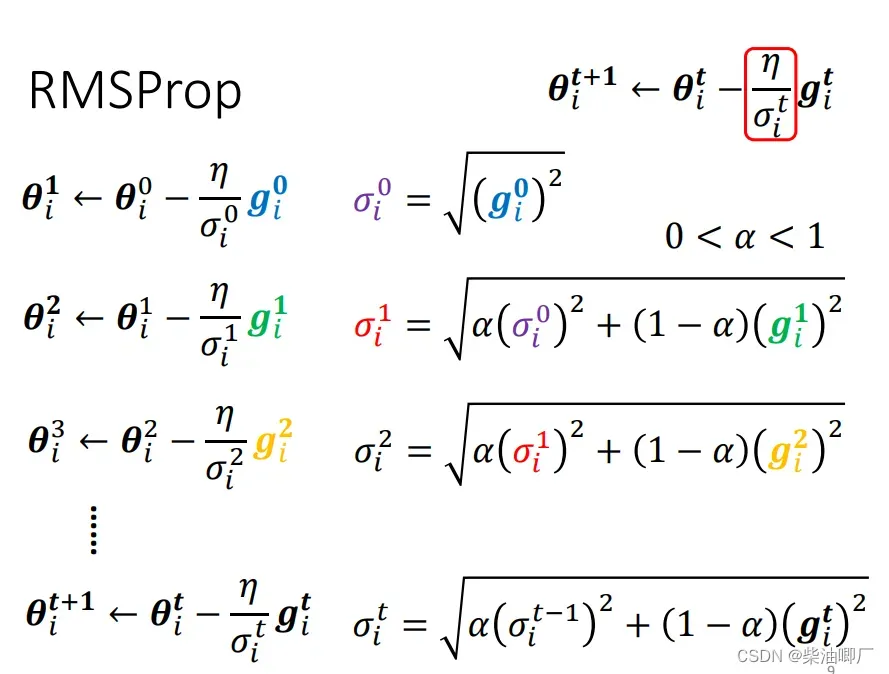
3. RMSProp + Momentum = Adam
现在我们经常使用的方法是RMSProp和Momentum相结合的方法。Pytorch已写好相关代码。
超参数需要自己调,一般使用预设的参数结果就比较好了。

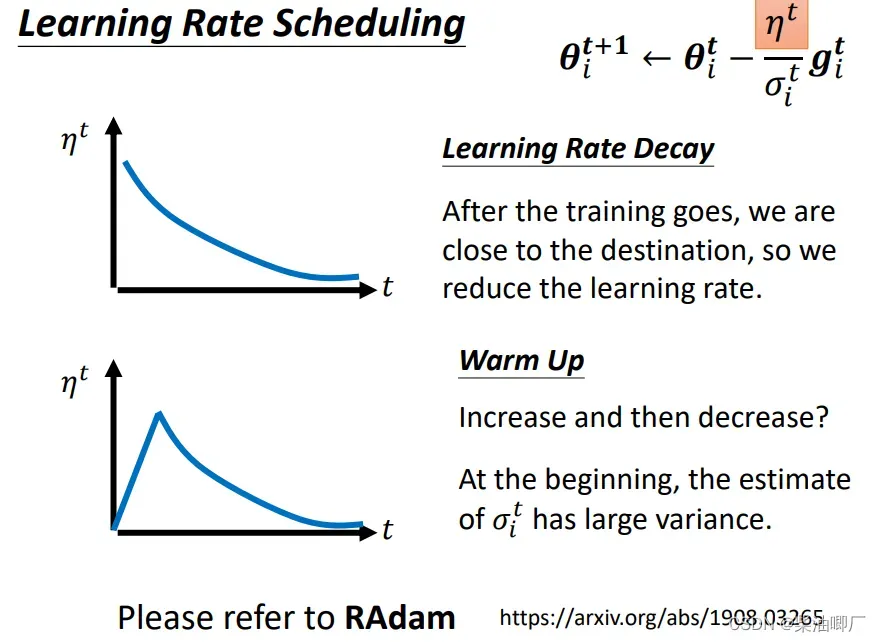
Learning Rate Scheduling
对于learningrate 本身的调参也有几种方法
-
Learning Rate Decay
随着时间的变化,越接近终点,变化速度越慢。 -
Warm Up
Learning rate 要先变大,后变小。
这种方法在Residual Network, Transformer 等地方都有当黑科技使用过。
先步伐小一点对error surface 进行探索,然后慢慢调大。
三部分的优化可以总结乘如下:
虽然momentum和sigma 都是有关过去Gradient之和,但是momentum是考虑正负方向的(direction),而sigma只考虑绝对值(magnitude)

除了改learning rate, 其他方法:
改error surface, 变得平滑。修改neural network etc.

4. 损失函数的定义可能改变模型训练的难度(Classification Short-Version)
https://speech.ee.ntu.edu.tw/~hylee/ml/ml2021-course-data/classification_v2.pdf
Classification 是特殊的Regression. Classification 在最后一步,会将连续的预测值转化成分类问题里的类别。
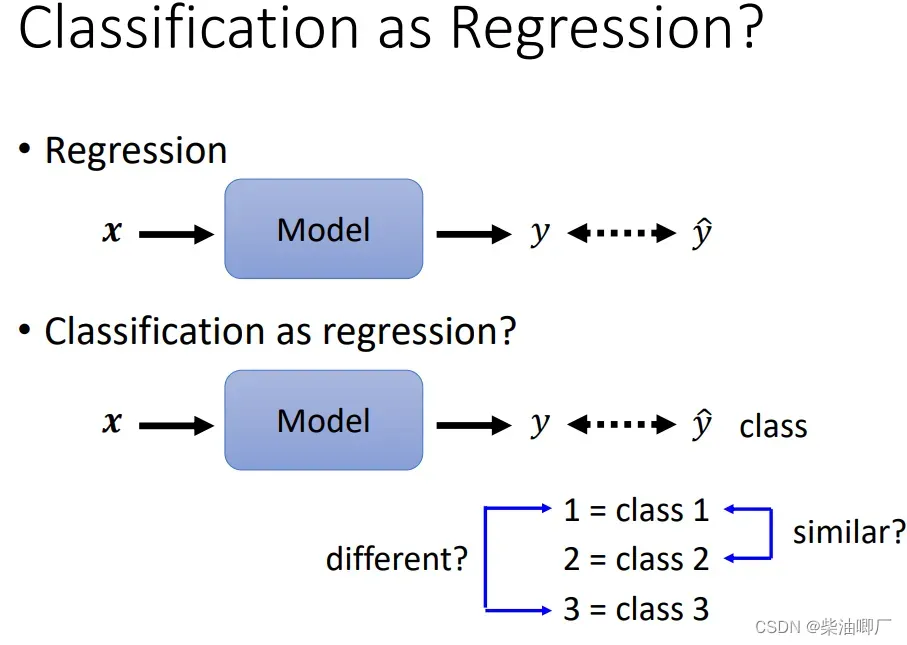
Regression预测的是一个值,而分类问题中转化成了one-hot 向量,一个向量里有多个值。
结构是相似的,只是output y变成多个yi, 每个yi都是由a1, a2, a3加上不同的权重和Bias得到。
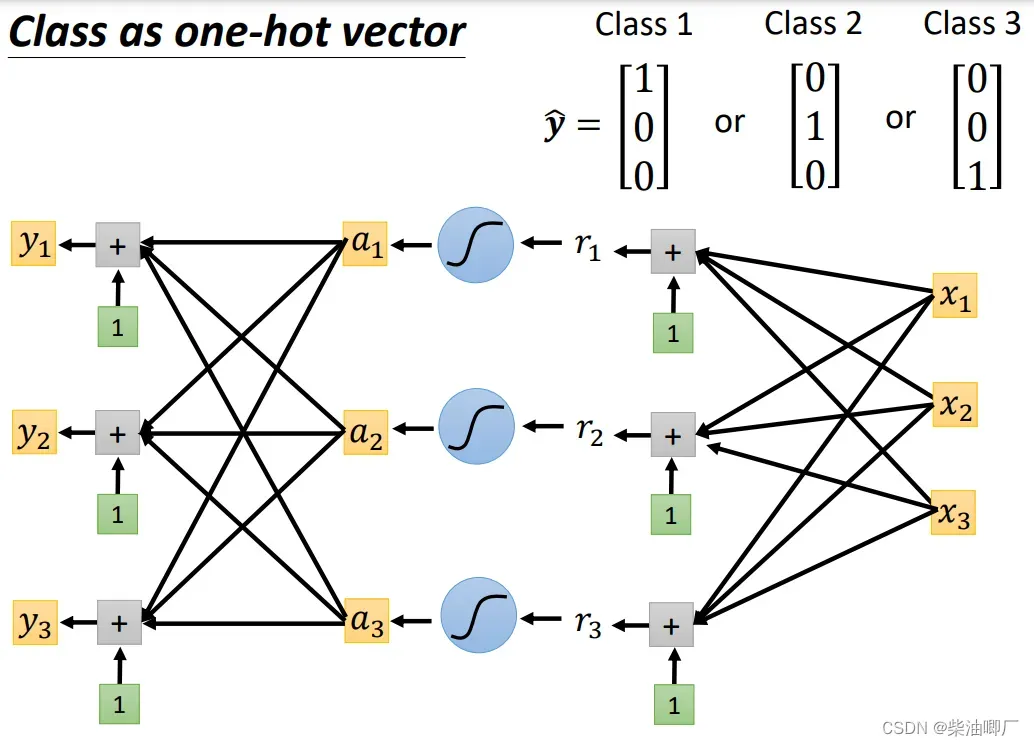
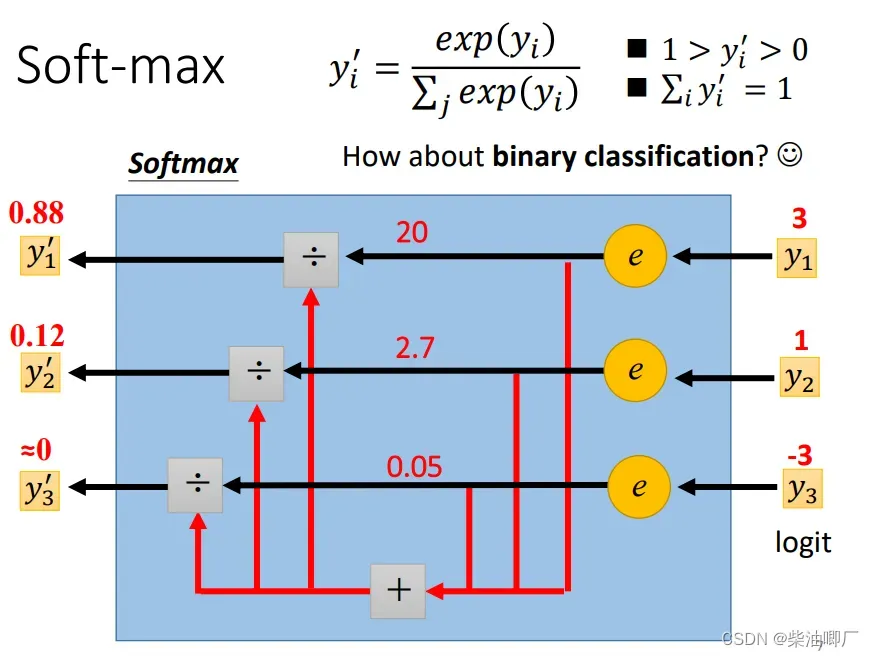
我们将可能是任何值得output y 转化成可以对应分类label的这个过程称为softmax.
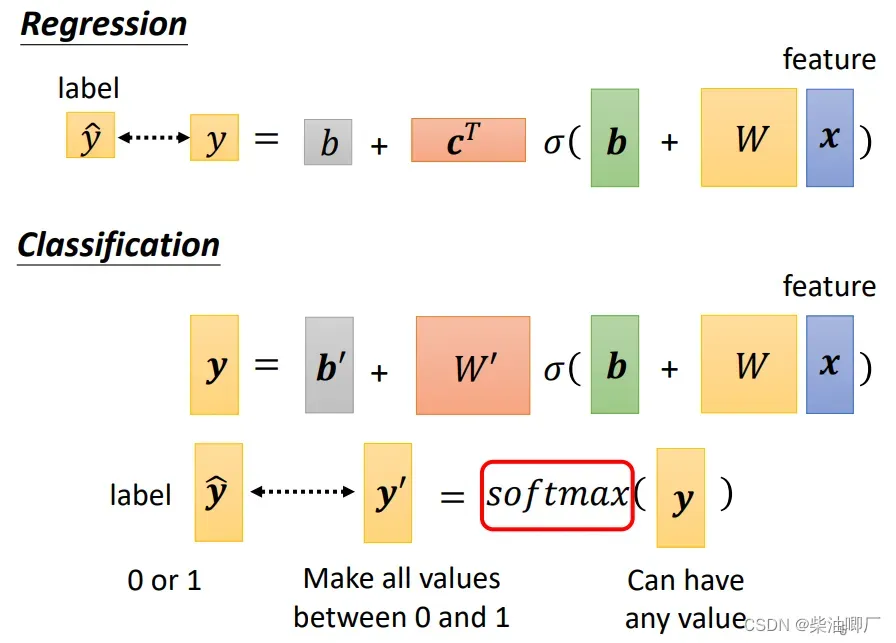
多分类中的转化公式如下,每个yi都会做一个指数运算,然后除以所有yi指数运算后之和,就可以把所有yi 转化成0-1之间的值。这样的处理方法还可以放大各个yi之间的差距。
如果是在二分类问题中,这个转化过程是sigmoid函数。softmax vs. sigmoid其实是等价的。
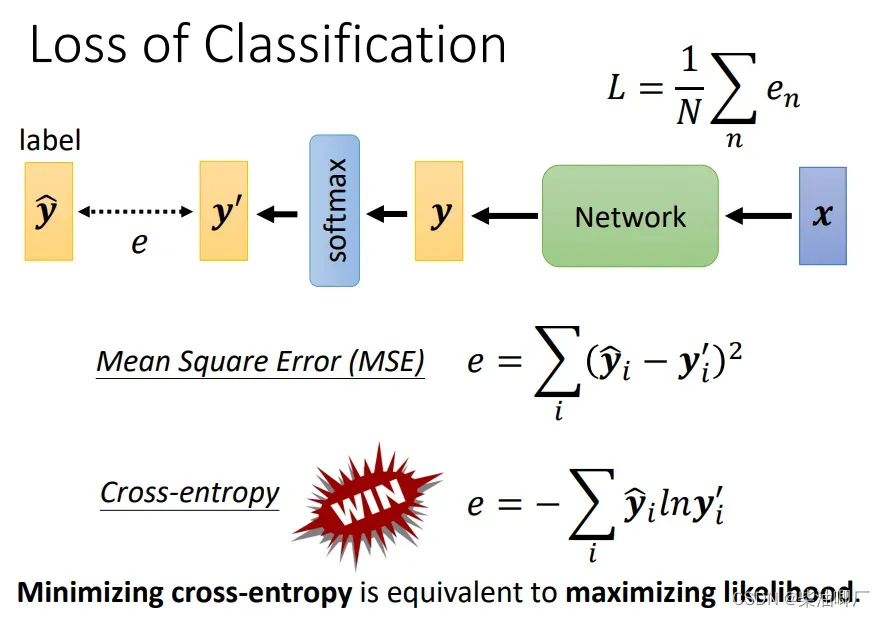
损失函数一般有以下两种。MSE vs. cross-entropy,分类问题用后者。
我们也经常听说最大似然估计,其实两者是一样的,只是不同的解释。
pytorch里,softmax 会加进cross-entropy的程序里面,不需要另外再加一步程序。
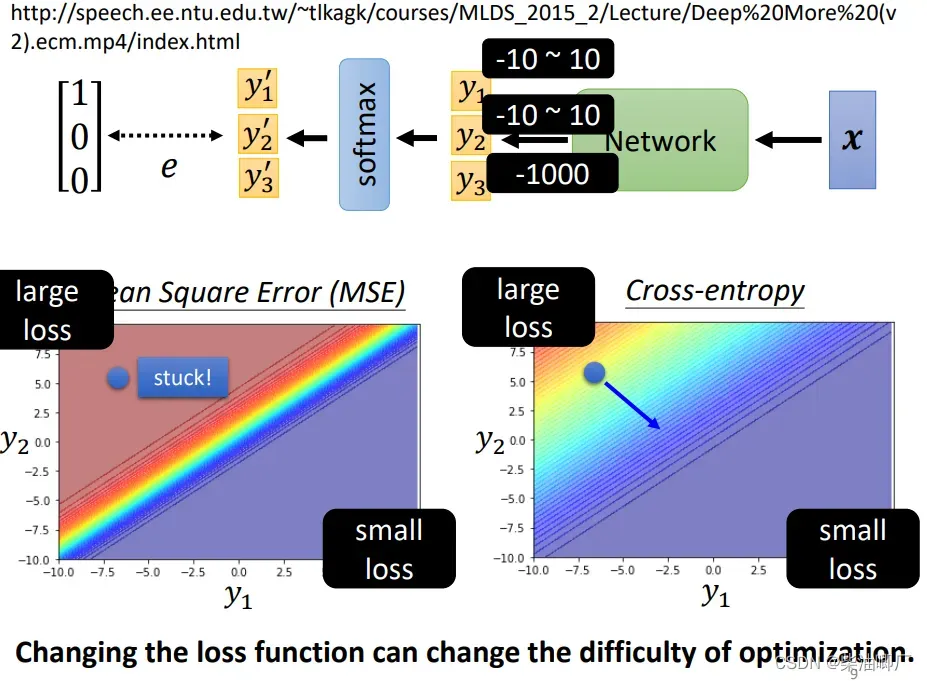
为什么在分类问题里loss function 使用Cross-entropy更好,而不是MSE?
假设三个yi。y1,y2 在-10~10之间,y3很小-1000最后的值会趋近于0,然后看y1,y2的变化对LOSS的影响。
MSE 有可能在初始的时候卡住,Gradient很小,很难发生Loss的变化,训练困难。
所以改变损失函数,也可以改变训练的难度。
Batch Normalization 批次标准化
Batch normalization can change the landscape of error surface.
我们都知道在模型训练前,会做feature normalization.
一般来说,标准化后的训练下降速度更快。
在DL中,做过标准化的X经过一个neuralnetwork会变成Z,再经过estimation function又会转变成a, 这时候Z, a都有了不同的data ranges. 所以我们希望在下一个neural network 之前,也对Z或者a 标准化。在Z或者a差距不大。
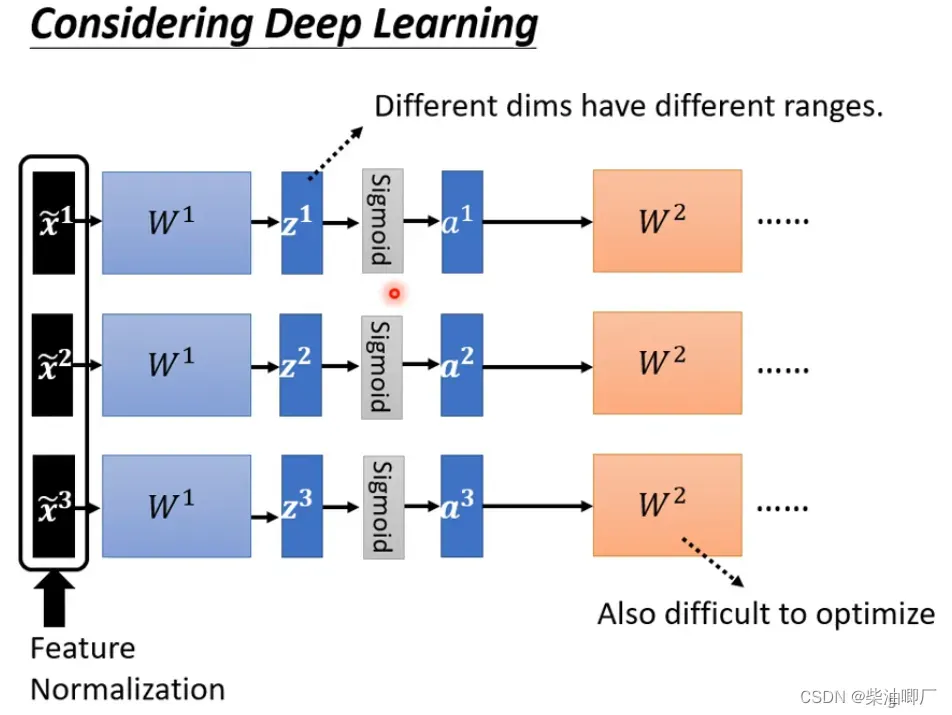
方法也是一样的,计算z的均值和方差,然后计算标准化的值。但如果是很大的network,这会产生很大的计算量。所以,引出了batch normalization 的概念,分batch做标准化。
当然这个batch不能太小,否则算不了。
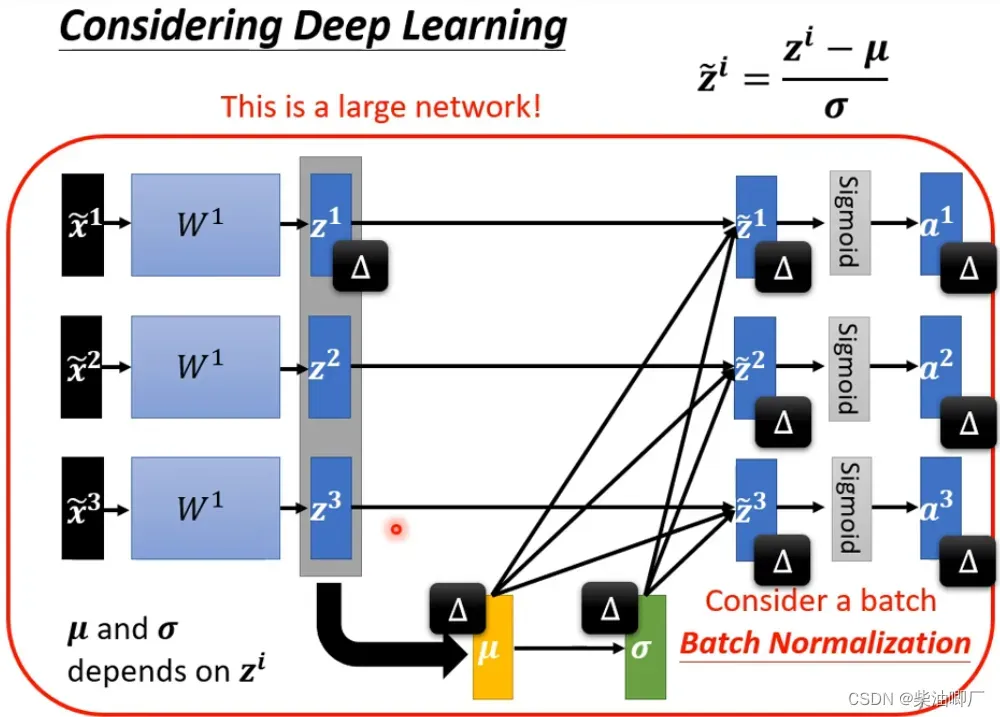
也会对标准化后的值,再加两个超参数gamma and beta,使得数据的分布不局限在均值为0,方差为1附近。gamma and beta的初始值是1 ,0 组成的向量,随着训练的进行然后调整
一开始的时候,dimension的分布是接近的,后续error surface的表现比较好之后,才会把beta和gamma加进去。
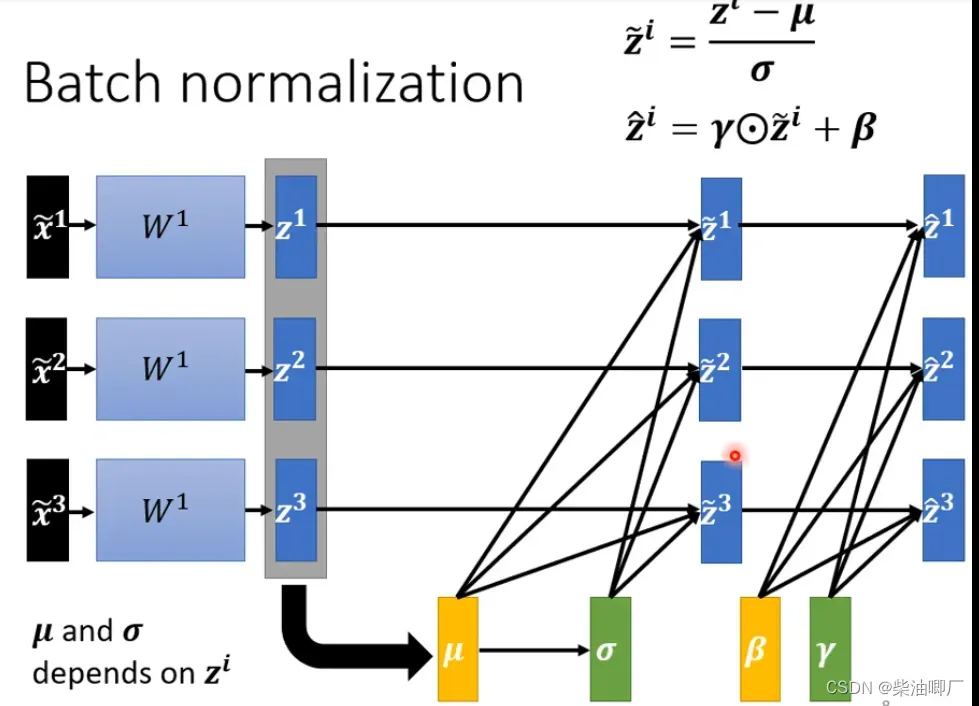
在训练集中,如果是在真正实际上线的应用中,不可能要等一个batch的数据量积攒后才开始训练。所以,在testing 阶段,借用training中miu and theta的滑动平均值。

文章出处登录后可见!
