写在前面:期刊《计算机研究与发展》;

1 摘要
- 【前人工作】SAX (symbolic aggregate approximation) 是一种符号化的时间序列相似性度量方法。
- 【缺点】采用PAA均值划分(目的是降维),但是均分点 是无法有效描述序列的形态变化的,所以导致序列间 在对应分段均值相似的情况下 得到的序列间的相似度是不科学不合理的!
- 【本文工作】在
SAX的基础上,提出了基于关键点的SAX改进算法,姑且称之为KP_SAX - 【本文算法的优点】该算法的相似性度量公式,既可以描述时间序列自身数值变化的统计规律(因为采用了均值点划分),又可以描述时间序列形态的变化(因为采用了关键点划分)
2 引言
- 【这句话多次出现,把引用给搬上来吧】
时间序列的相似性度量是衡量两个时间序列相义程度的方法,它是时间序列分类聚类异常发现等诸多数据挖掘问题的基础,也是时间序列挖掘的核心问题。

SAX (symbolic aggregate approximation)是一种运用符号化方法对时间序列进行表示、维度约简及相似性度量的方法,运用时间序列内在的统计规律对数据进行离散化及符号表示,得到时间序列的字符表示。
通过字符之间的距离,从而得到时间序列之间的相似度。
2.1 SAX的缺点+ 举个例子分析
SAX方法采用PAA算法将时间序列平均划分,均分点 无法有效描述序列的形态变化,导致序列在对应分段的均值相等的情况下,无法有效计算序列之间的相似度。
-
如下图,展示了两个时间序列,C和Q,以及它们标准化处理后的图像 和 正态分布图像
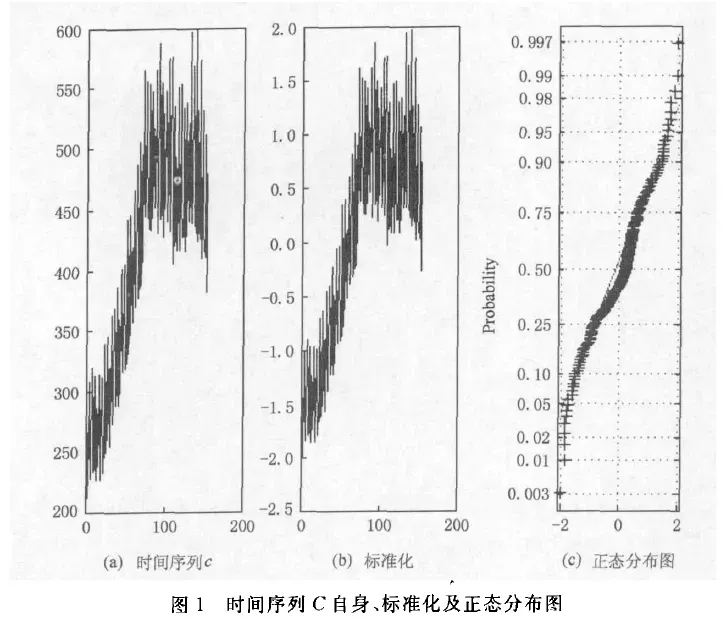
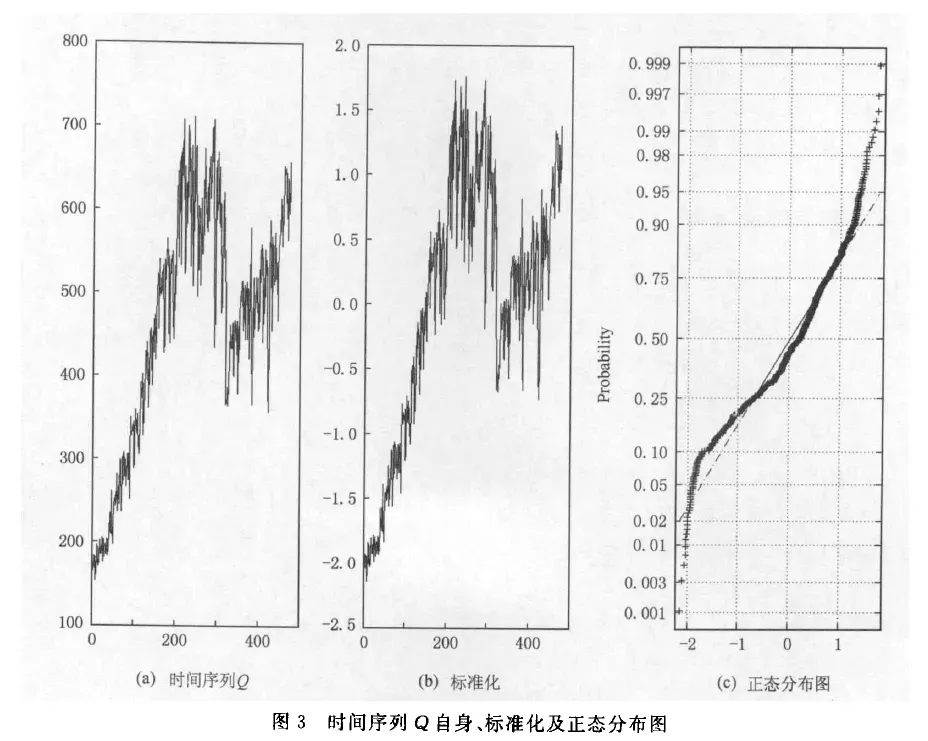
-
根据我的主观分析,序列C长度是200,在90-180期间比较密集,没有太大的波动;
-
而序列Q 的长度是500,在300左右有一个明显下降的趋势;
-
所以,我认为这两个时间序列是不相似的,毕竟趋势都不一样。
-
但是,如果使用SAX方法来计算,他们两个序列的相似性居然是100%?
看一下计算过程:
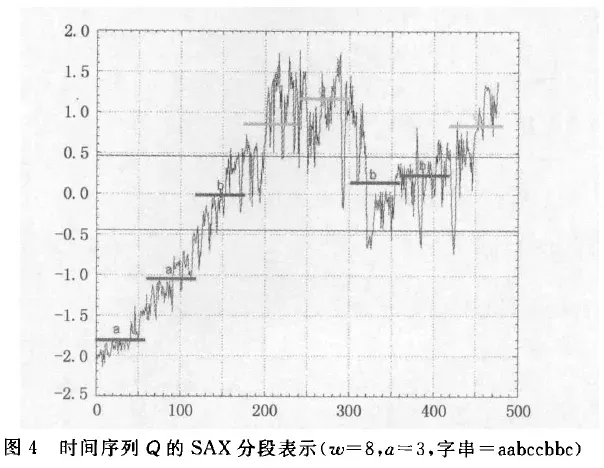
① 两个序列 分别均分为8段,每一段会用一个符号表示。得到的结果如下:
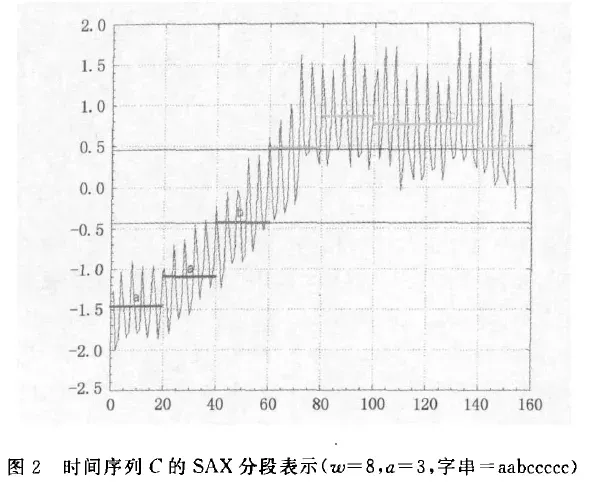
- C 这个时间序列的长度就从200降到了8,是
aabccccc - Q 这个时间序列的长度就从500降到了8,是
aabccbbc
【我的胡乱分析】到目前为止,无论是分段表示,还是符号表示,都能够发现在中后期,这两条序列是不一样的,所以说,最后的相似度为0应该不能全怪SAX算法,因为到目前来说,都是十分正常的!
所以我认为是,计算符号距离的锅。其实可以使用编辑距离!
- SAX 所采用的相似度量公式(非常鸡肋)!

2.2 分析问题原因
- SAX 基于PAA算法等长划分,划分位置对于SAX的度量结果有直接的影响;【不能只考虑均值点】
- SAX算法无法区分 紧邻的字符之间的距离,比如说a和b之间的距离 = b和c之间的距离,但是事实却不是这样!【距离度量不行!】
2.3 本文的改进工作
-
利用 均分点 + 关键点 对序列进行分段,既考虑了序列自身概率分布的变化,又兼顾到序列形态的变化!!!
-
度量算法:改进为“基于关键点的相似性度量算法”,将符号序列转换为字符换的形式,并依据算法相关的符号距离计算公式 将字符距离转换为两时间序列间的相似度距离。【好像也没说清楚。。。】
3 实验结果与分析
数据:Rothamsted地区的 1852年 -1925 年 的4个时间序列(也没说清楚啊,时间的单位?记录数据的单位?)
算法:本文—— KP_SAX 对比实验 —— SAX
3.1 关键点的选取规则
- 符号说明

- 极值点EP 成为 关键点 KP的条件是:

- 怎么开始证明定理了???没啥好看的,乱起八糟的,这个没有应用价值啊!这个时间复杂度这么高。。。。。



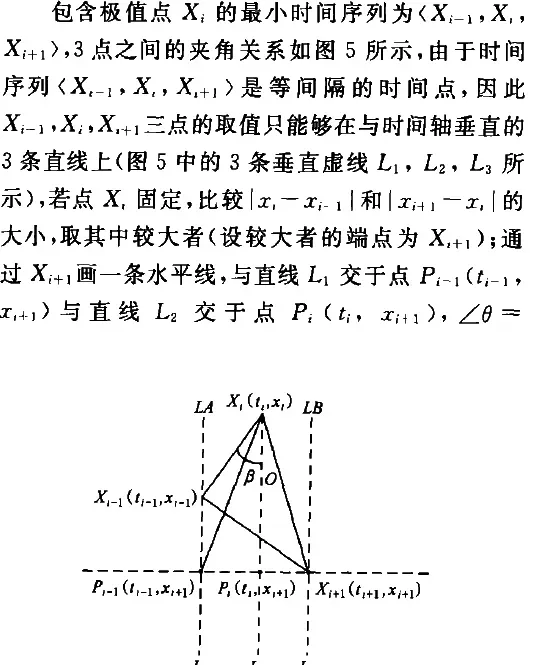

3.2 本文定义的相似度距离计算公式

3.3 开始做实验了
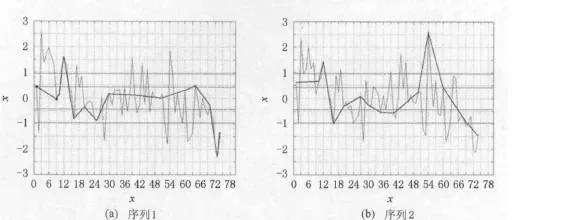
- 4个时间序列,以及对应的正态分布图长这样:
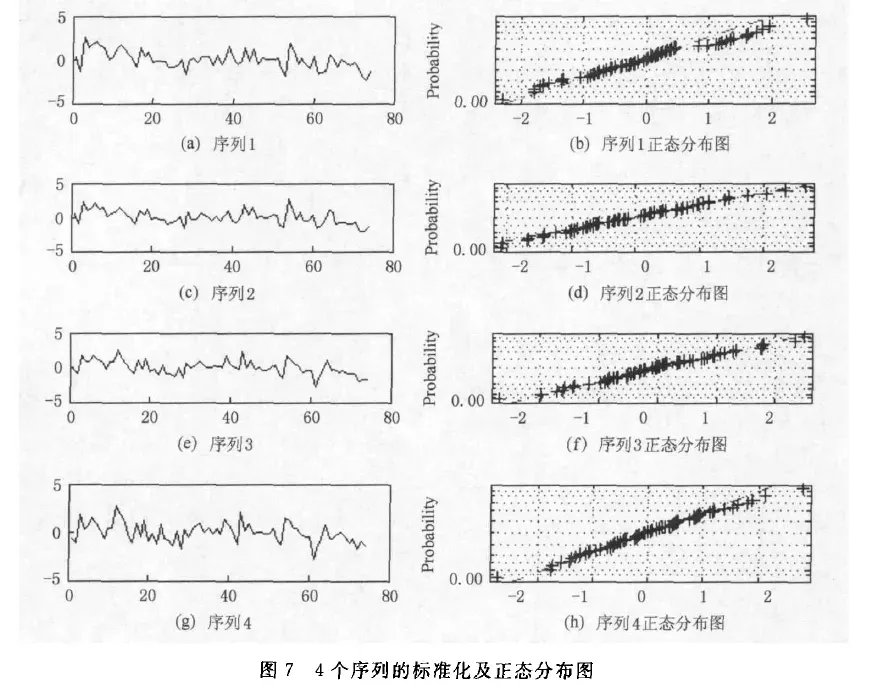
- 用SAX算法进行实验
- PAA是不能有效描述序列的形态变化的,因为它认为每个点再序列中的作用都是等同的。

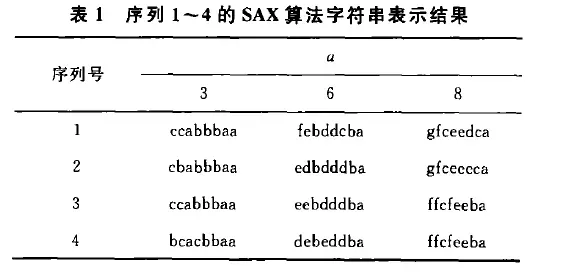
- 对于SAX_KP来说,会在PAA的分8段的基础上,保留关键的极值点。
- 放到例子里面说,比如说序列2,就能很好地捕捉到54 左右的一个极大值点,从而更加有效的描述出了序列形态!
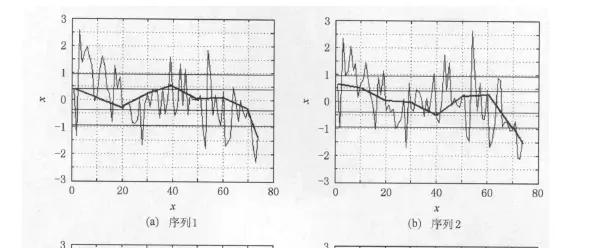

3.4 结论
实验数据表明,SAX对4个序列计算相似度的结果均为0,无法有效区分之间的相似性;
改进算法虽然部分提高了算法的复杂度,但可以有效计算各序列间的相似度距离,达到了改进的目的。
4 总结
- 本文在SAX均分段的基础上,以各个子段为单位,进行符号化表示以及比较,因此可以更好地描述时间序列的形态变化。
文章出处登录后可见!
