论文链接：


https://arxiv.org/pdf/2202.07082.pdf

 

目录

摘要

        近年来，图神经网络（GNNs）快速发展，使无数的图分析任务和应用受益。一般来说，大多数图神经网络依赖于同质性假设，即属于同一类别的节点更有可能被连接。然而，作为众多现实世界场景中普遍存在的图的属性，异质性，即具有不同标签的节点倾向于被连接，大大限制了定制的同质性GNN的性能。因此，异亲图的GNNs在这个社区中得到了越来越多的关注。据我们所知，在本文中，我们首次对嗜异性图的GNNs进行了全面的回顾。具体来说，我们提出了一个系统的分类法，该分类法从本质上管理着现有的异质性GNN模型，同时还提出了一般的总结和详细的分析。此外，我们总结了主流的异质图的基准，以促进稳健和公平的评价。最后，我们指出了潜在的方向，以推进和激励未来对异质图的研究和应用。

1 绪论

        图是无孔不入的结构化数据，已被广泛应用于许多现实世界的场景，如社交网络[Tang等人，2009；Peng等人，2022]、知识库[Vashishth等人，2019]、交通网络[Wu等人，2020b]和推荐系统[Ying等人，2018；Ma等人，2019]。最近，图神经网络（GNN）凭借强大的学习能力取得了显著的成就，成为解决各种图分析任务的普遍模型，如节点分类、链接预测和图分类[Kipf and Welling, 2017; Hamilton et al., 2017; Vashishth et al., 2019; Veliˇckovi ́c et al., 2018]。        

        虽然已经设计了大量具有不同结构的GNNs[Xu等人，2019；Wu等人，2020a；Zhu等人，2020b；Liu等人，2022]，但其中大部分都遵循同质性假设，即具有相似特征或相同类别标签的节点被连接在一起。例如，在引文网络中，一项研究通常会引用来自同一研究领域的参考论文 [Ciotti et al., 2016]。然而，现实世界的图并不总是遵守同质性假设，而是显示出相反的属性，即异质性，即链接的节点具有不同的特征和不同的类别标签。例如，在在线交易网络中，欺诈者更有可能与客户而不是其他欺诈者建立联系[Pandit等人，2007]；在约会网络中，大多数人喜欢与异性约会[Zhu等人，2021]；在分子网络中，蛋白质结构更有可能由不同类型的氨基酸组成，它们被联系在一起[Zhu等人，2020a]。图1中提供了亲同性和亲异性图的例子，以直观地说明它们的区别。重要的是，这种异质性限制了现有的异质性GNN在一般图形结构数据上的学习能力，导致异质性图形的性能明显下降。

        GNN 对 Heterophily 的挑战是什么？我们将性能下降归因于同质设置下的统一消息传递框架。该框架的过程可以概括为：首先聚合从本地邻居节点提取的消息，然后用聚合的邻居消息更新最终的自我节点（当前中心节点本身）表示。然而，在异质性设置下，这种机制主要有两个棘手的局限性：

        (1) 局部邻居被定义为图拓扑中的近端节点，它们无法捕获具有长期距离的信息节点；在异质图上，具有高度结构和语义相似性的节点可能彼此远离。

        （2）统一聚合和更新忽略了相似和不相似邻居之间的信息差异。

        在异质图上，判别节点表示学习渴望以不同的信息传递来获得可区分的信息。

        鉴于这些挑战，最近，越来越多的研究人员开始将注意力转向对具有异质性的 GNN 的研究。研究重点足够广泛，来自异质图数据探索 [Lim et al., 2021b;林等人，2021a； Yan et al., 2021] 到各种技术算法开发 [Bo et al., 2021;杨等人，2021； Chien 等人，2020]。事实上，异质图学习由于其巨大的潜力正在成为一个上升趋势的研究课题。这背后的原因主要有以下几个方面：

        （1）具有异质性的图结构数据在现实世界中广泛存在，从日常生活的人际关系到科学的化学分子研究。异质图的相应应用在学术界和工业界都是光明的前景；

         (2) 异质性图分析任务仍然是开放且有前途的研究课题，而设计强大且富有表现力的异质性 GNN 模型需要解决许多挑战。因此，有必要且及时地概述现有的异质图学习方法；

        在本文中，我们对异质图的GNN进行了全面系统的回顾，以提供异质图研究的总体蓝图。据我们所知，这是第一次在不同的异质性GNN方法之间建立联系并进行比较，从而深入了解不同的方法如何应对挑战。我们期望我们的调查将极大地激发和促进异亲图形的发展。我们工作的贡献总结如下。

        – 全面概述。我们从数据、算法和应用等方面对当前的异质性GNN进行了全面的概述。我们提供了每种模型类型的详细描述，以及必要的比较和要点总结；

        – 系统化的分类法。我们提供了一个系统的异质性GNN分类法，并将现有的方法分为两类，即非本地邻居扩展和GNN架构细化；

        – 未来的方向。我们提出了有希望的未来再搜索方向，并从多个角度讨论了现有的异质性GNN的局限性，即可解释性、稳健性、可扩展性和异质性图形数据探索。

2 初步措施

        符号。让G = (V,E) 是一个无定向、无权重的图，其中是节点集，是边集。节点v的邻居集表示为。节点特征由特征矩阵表示，其中第i行是节点的特征向量，d是特征的数量.

        问题设置。现有的工作主要集中在半监督性节点分类的问题上。在这个任务中，假设每个节点 v 属于 C 类中的一个，在训练节点集中只有一部分节点被提供标签为 。 该任务的目标是预测未给出标签的节点的类别。

        图形神经网络。一般来说，GNN采用的是消息传递机制，每个节点表征的更新是通过聚合本地邻居表征的消息，然后将聚合的消息与它的自我表征相结合[Xu等人，2019]。每个节点v∈V的第l个GNN层的更新过程可以描述为：

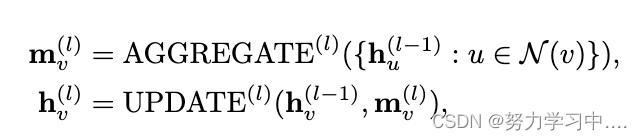
         其中和分别代表第l层节点v的消息向量和表示向量。

        AGGREGATE(·) 和 UPDATE(·) 分别是聚合函数（例如均值、LSTM 和最大池化）和更新函数（例如线性层组合）[Hamilton et al., 2017]。

        给定第一层的输入为 ，L 层 GNN 每一层的学习节点表示可以表示为，对于 和 l = (1,··· ,L)。对于节点分类任务，最终节点表示 将被送到分类器网络（例如，全连接层）以生成类别的预测。

        异质性和同质性的测量。一般来说，图 G = (V,E) 的异质性和同质性可以通过两个指标来衡量：节点同质性 [Pei et al., 2020] 和边同质性 [Zhu et al., 2020a]。具体来说，节点同质性 是每个节点具有相同类别的邻居的平均比例：

         边同质性 是连接具有相同类别的两个节点的边的比例：       

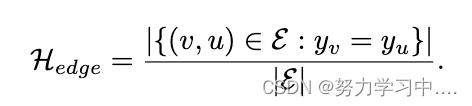
         和的范围是[0,1]。具有强烈同质性的图形具有较高的和（更接近于1）；而具有强烈异质性的图形具有较小的和（更接近于0）。

 3 具有异质性的 GNN

         所提出的算法分类如图 2 所示。从消息传递机制的角度来看，现有的异质性 GNN 可以分为两组，即（1）非局部邻居扩展方法； (2) GNN 架构细化方法。这两个类别对应地解决了两个关键问题：

        (1) 如何发现合适的邻居；

        (2) 如何利用来自已发现邻居的信息。 具体来说，非局部邻居扩展方法可以进一步分为两个子类别，即高阶邻居混合和潜在邻居发现，两者都致力于修改方程式中邻居集 N(v) 的定义。

        另一方面，GNN架构细化方法可以进一步分为三个子组，即自适应消息聚合、自我邻接分离和层间组合方案，分别在函数AGGREGATE(·)、UPDATE(·)和GNN分层架构上工作。

        我们在表1中总结了不同的GNNs采用的异质性方法的技术。可以看出，一些方法将不同的技术正交地结合起来，以获得更强大和更有表现力的异质性GNN。

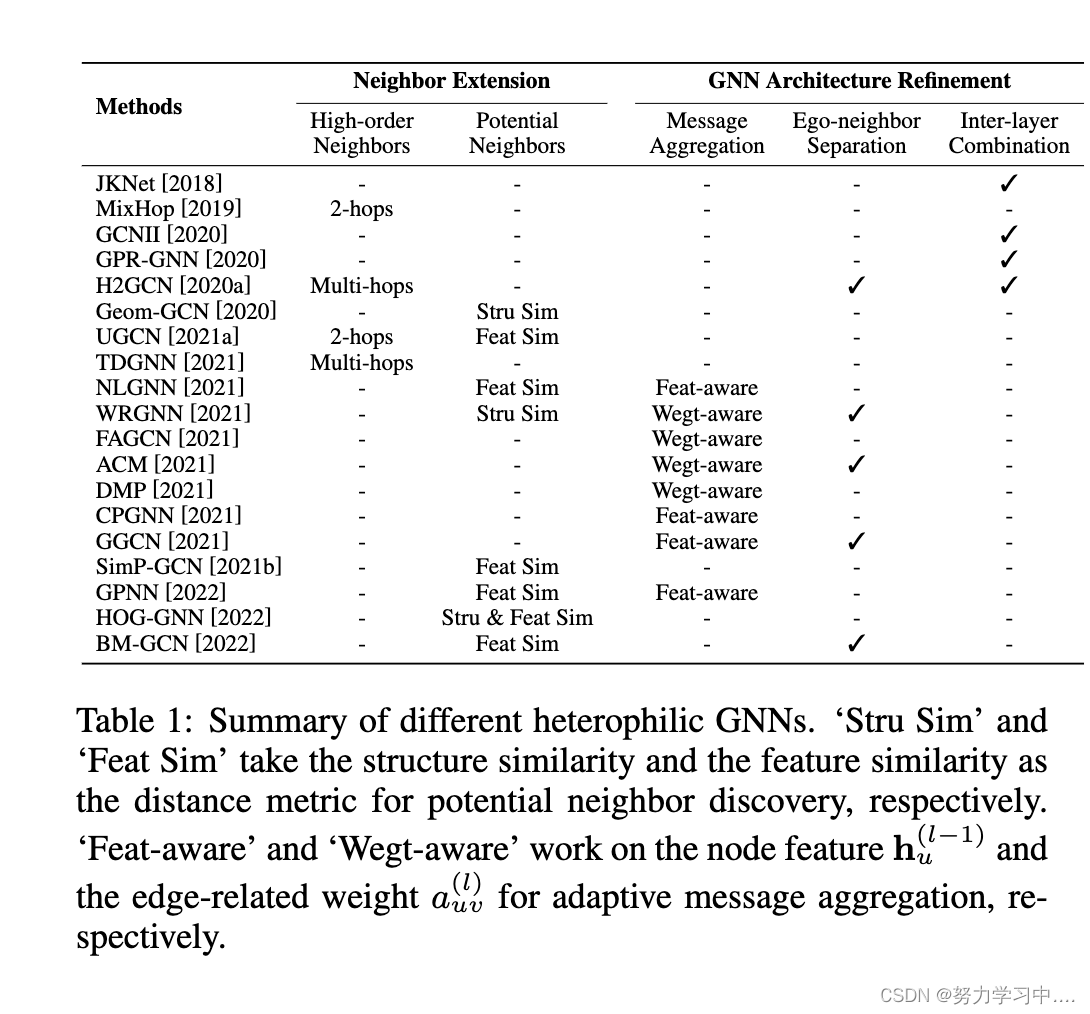
 （不同的异质性GNN的总结。"Stru Sim "和 "Feat Sim "分别将结构相似性和特征相似性作为发现潜在邻居的距离指标。"Feat-aware "和 "Wegt-aware "分别以节点特征和边相关权重作为自适应信息聚合的工作依据。）

 3.1 Non-local Neighbor Extension

        在同质图的统一消息传递框架下，邻域通常被定义为一跳远的所有邻居的集合（例如，GCN），这意味着只有来自图中近端节点的消息被聚合。然而，这样的局部邻域定义可能不适用于异质图，其中同一类的节点表现出高度的结构相似性，但可能彼此相距较远。鉴于这些，当前的异质性 GNN 主要通过两种方案尝试将本地邻居扩展到非本地邻居：高阶邻居混合和潜在邻居发现。因此，通过从遥远但信息丰富的节点捕获重要特征，可以显着提高异质性 GNN 的表示能力。这两个方案的更多细节可以在下面找到。

        高阶邻居混合

        高阶邻居混合允许自我节点从他们的本地一跳邻居和更远的k跳邻居那里接收潜意识表征，因此，异质GNN可以混合来自不同距离的邻居的潜意识信息。形式上，k-hop邻居集被定义为，其中d(u,v)衡量节点u和v之间最短的距离。

        MixHop[Abu-El-Haija等人，2019]是一种有代表性的方法，它聚合了多跳邻居的消息。除了一跳邻居，MixHop还考虑两跳邻居进行消息传播。之后，从不同地点获得的信息通过不同的线性转换进行编码，然后通过串联进行混合。

        与MixHop类似，H2GCN[Zhu等人，2020a]也在每个消息传递步骤中对高阶邻居的信息进行汇总。为了提供理论支持，H2GCN验证了当一跳邻居的标签有条件地独立于自我节点的标签时，两跳邻居倾向于涉及更多与自我节点具有相同等级的节点。按照类似的想法，UGCN[Jin等人，2021a]利用两跳网络作为传播图之一来执行消息传递。为了控制两跳邻居集的规模，UGCN进一步重新定义了两跳邻居集，其中的节点至少有两条不同的路径通往连接的自我节点。此外，TDGNN [Wang and Derr, 2021]利用树状解构，将不同k-hops的邻居分成多个子图，然后并行传播这些子图上的信息。

        潜在的邻居发现

        与直接利用图的固有结构信息的高阶邻居混合方法相比，潜在邻居发现方法重新考虑了异质图中邻居的定义，并通过整个拓扑探索与异质性建立了创新的结构邻居。除了原来的邻居集，这些方法还构建了一个新的潜在邻居集，其中s(u,v)是一个度量函数，用来衡量节点u和v在一个特定定义的潜在空间中的距离，τ是一个限制邻居数量的阈值。

        通常，Geom-GCN[Pei等人，2020]将输入图映射到一个连续的潜在空间，并定义了几何关系，即分割的二维欧几里得几何位置，作为发现潜在邻居的标准。除了原始输入图中的固有邻居，符合定义的几何关系的邻居也参与到GCN的信息聚合中。此外，NL- GNN [Liu et al., 2021] 和 GPNN [Yang et al., 2022] 采用关注机制或利用指针网络，根据关注分数或与自我节点的相关关系对潜在邻居节点进行排序。通过这种方式，可以发现并选择异质图中与自我节点最相似的潜在邻居。

        HOGGCN [Wang et al., 2022]用标签传播技术构建了一个同质性程度矩阵，以探索一对节点在整个异质性图中属于同一类别的程度。通过在传播过程中涉及阶级意识的信息，具有较高异质性（即较低的同质性程度）的阶级内节点将比没有异质性的阶级间节点对邻居聚合的贡献更大。

        考虑到节点的相似性，UGCN[Jin等人，2021a]和SimP-GCN[Jin等人，2021b]通过kNN算法为每个自我节点选择特征级余弦相似度最高的k个相似节点对来构造邻居集。相比之下，WRGNN[Suresh等人，2021]将邻居节点的度数序列作为衡量自我节点之间结构相似性的标准，以重建一个图，其中不同的邻居由不同的边缘关系来表示。

        此外，BM-GCN [He et al., 2022]基于块相似度矩阵构建了一种新的网络拓扑，从而可以探索块引导的邻居，并对异性节点进行不同聚合规则的分类聚合。

3.2 GNN Architecture Refinement

        公式(1)中的一般GNN架构包含两个基本组成部分：聚合函数AGGREGATE(·)整合来自发现的邻居的信息，以及更新函数UPDATE(·)将学到的邻居信息与初始的自我表示相结合。考虑到异质图上的原始本地邻居和扩展的非本地邻居，现有的GNN结构细化方法通过相应地修改AGGREGATE(·)和UPDATE(·)，从以下几个方面促进了对邻居信息的充分利用：

        (1) 自适应消息聚合可以区分相似邻居和不相似邻居的消息。

        (2)自我-邻居分离侧重于自我表征和其邻居信息之间的差异；

        (3)层间组合强调不同传播范围（即GNN层数）对节点表征学习的影响。

        所有这三个方面都是为了同一个目的：通过鼓励区分性和鉴别性的节点表示，提高GNN对异质图的表达能力。

自适应消息聚合

        给定要聚合的邻居，在异质图上集成有益消息的关键是区分相似邻居（可能属于同一类）和不同邻居（可能属于不同类）的信息。为了使异质图上的节点表示更具区分性，自适应消息聚合方法通过在第 l 层为节点对 (u,v) 施加自适应边缘感知权重 来改变聚合操作AGGREGATE(·)：

        这样，不同的方法为制定了不同的权重分配方案，以模拟聚集过程中相似和不相似的邻居的重要性。在下文中，我们将分别介绍现有方法在谱域和空间领域所采用的权重分配方案的细节。具体来说，频谱GNN利用图信号处理理论来设计图滤波器，而空间GNN则关注图的结构拓扑结构来制定聚合策略。 

        在频谱领域，与拉普拉斯平滑[Li et al., 2018]和低通滤波[Wu et al., 2019]在同质图上近似图傅里叶变换不同，异亲图上的频谱GNN同时涉及低通和高通滤波器来自适应提取低频和高频图信号。这背后的基本直觉在于，低通滤波器主要重新保持节点特征的共性，而高通滤波器则捕捉节点之间的差异。

         通常，FAGCN[Bo等人，2021]采用自门控机制，通过将分成两个部分，即和，分别对应于低通和高通滤波器来学习低频和高频信号的比例。通过自适应的频率信号学习，FAGCN可以在不同类型的图上实现同质性和异质性的表现力。除了低通和高通滤波器，ACM[Luan等人, 2021]还涉及到身份滤波器，它是低通和高通滤波器的线性组合。这样，ACM可以自适应地利用每个节点的不同滤波通道的有益邻居信息；同时，其身份滤波器可以保证输入信号的形成损失较小。

        在空间领域，异质GNNs需要对来自相同或不同类别的邻居进行基于拓扑结构的多样化聚合，而不是在异质GNNs中进行平均聚合。因此，邻居的边缘感知权重应该根据空间图拓扑和节点标签来分配。DMP方法[Yang等人，2021]将节点属性作为弱拉贝尔，考虑到节点的异质性以实现多样化的信息传递，并在每条边上指定每个属性传播权重。DMP不是用标量权重来聚合节点层面上具有相同权重的所有节点属性，而是通过在属性二元中操作，将权重扩展为矢量，该矢量可以通过将GAT[Veliˇckovíc等人，2018]的权重放宽为实值或允许对邻居权重进行元素维度平均来计算。相比之下，WRGNN [Suresh等人，2021]首先将原始的input heterophilic图转换为多关系图，在关系边上建立heterophily模型，然后用明确的链接权重进行关系聚合。

        除了自适应边缘感知权重学习之外，还有另一种解决方案通过修改等式（4）中的 来进行邻居表示学习。 传统上，上述方法主要利用邻居的上下文节点表示。相比之下，该解决方案将上下文节点嵌入转换为反映异质性的其他节点级属性。通过这种方式，异质性 GNN 可以捕获异质性的有益信息，用于可区分的节点表示学习。通常，CPGNN [Zhu et al., 2021] 不是传播原始节点特征表示，而是传播基于兼容性矩阵的先验信念估计，因此它可以通过建模之间连接的可能性来捕获异质性和同质性。不同类的节点。此外，GGCN [Yan et al., 2021] 使用余弦相似度在一定的相对节点度约束下发送有符号的邻居特征。通过这种方式，允许消息可选地乘以负号或正号。

         直观地说，签名信息包括由对立类的邻居发送的否定信息，以及由同一类的邻居发送的肯定信息。除了统一的GCN聚合，NLGNN[Liu等人, 2021]和GPNN[Yang等人, 2022]考虑了顺序聚合，其中邻居是根据类的相似性按顺序排列的。一个常规的一维卷积层被应用于提取顺序节点之间的亲缘关系，无论这些节点在异质图中是接近还是疏远。

         自我邻居分离

        在异质图上，一个自我节点很可能与它的邻居在类别标签方面是不一样的。因此，将自我节点表征与邻居节点的聚合表征分开编码将有利于可区分的节点嵌入学习。详细地说，自我邻接分离方法在AGGREGATE(·)中分离了自我节点的自环连接。同时，他们将UPDATE(·)改变为非混合操作，如连接，而不是混合操作，如vanilla GCN中的 "平均"。

        H2GCN [Zhu et al., 2020a]首先提出排除自环连接，并指出更新函数中的非混合操作可确保富有表现力的节点表征在多轮推进中生存，而不会变得过于相似。此外，WRGNN[Suresh等人，2021]对自我节点嵌入及其邻居聚合消息施加了不同的映射函数，而GGCN[Yan等人，2021]将映射函数模拟为可学习的标量参数，以单独学习自我邻居表征。此外，ACM[Luan等人，2021]采用身份过滤器来分离小我嵌入，然后在更新函数中与其邻居信息进行通道级组合。

        层间组合

        与自适应消息聚合方法和自我邻接分离方法不同，层间组合方法通过深入研究GNN的每一层来处理异质图，考虑层间操作来提高GNN在异质情况下的表示能力。这种策略背后的直觉是，在GNN的浅层中，它们收集局部信息，例如两层香草GCN中的一跳邻居定位，当层数越深，GNN逐渐通过多轮邻居传播隐含地捕获全局信息。在异质性设置下，具有相似信息（即类标签）的邻居可能位于局部几何和长期全局拓扑中。因此，结合各层的中间表征，有助于利用不同的邻居范围，考虑到局部和全局的结构特性，从而形成强大的异质性GNNs。

        之前的想法首先来自JKNet[Xu等人，2018]，它灵活地捕捉了同质性设定下不同邻域范围的更好的结构感知表示。由于异质图的结构拓扑比较复杂，H2GCN [Zhu et al., 2020a]受到启发，将之前所有层的节点表示串联起来，在最后一层单独学习异质节点特征。

        与H2GCN使用之前所有的中间表征相比，GCNII [Chen et al., 2020]只将每层的第一层节点嵌入与初始残差连接整合在一起。GPR-GNN[Chien等人, 2020]没有使用简单的连接操作，而是进一步分配可学习的权重，通过广义PageRank（GPR）技术自适应地结合各层的表征。因此，层间组合方法能够进行拓扑特征探索，并受益于信息量大的多轮传播，使异质图的节点特征得以区分。

4 真实世界的基准

        为了为异质图学习的发展提供数据支持，我们收集并列出了当前异质图数据集的真实世界基准，并进行了详细的统计，如表2所示。

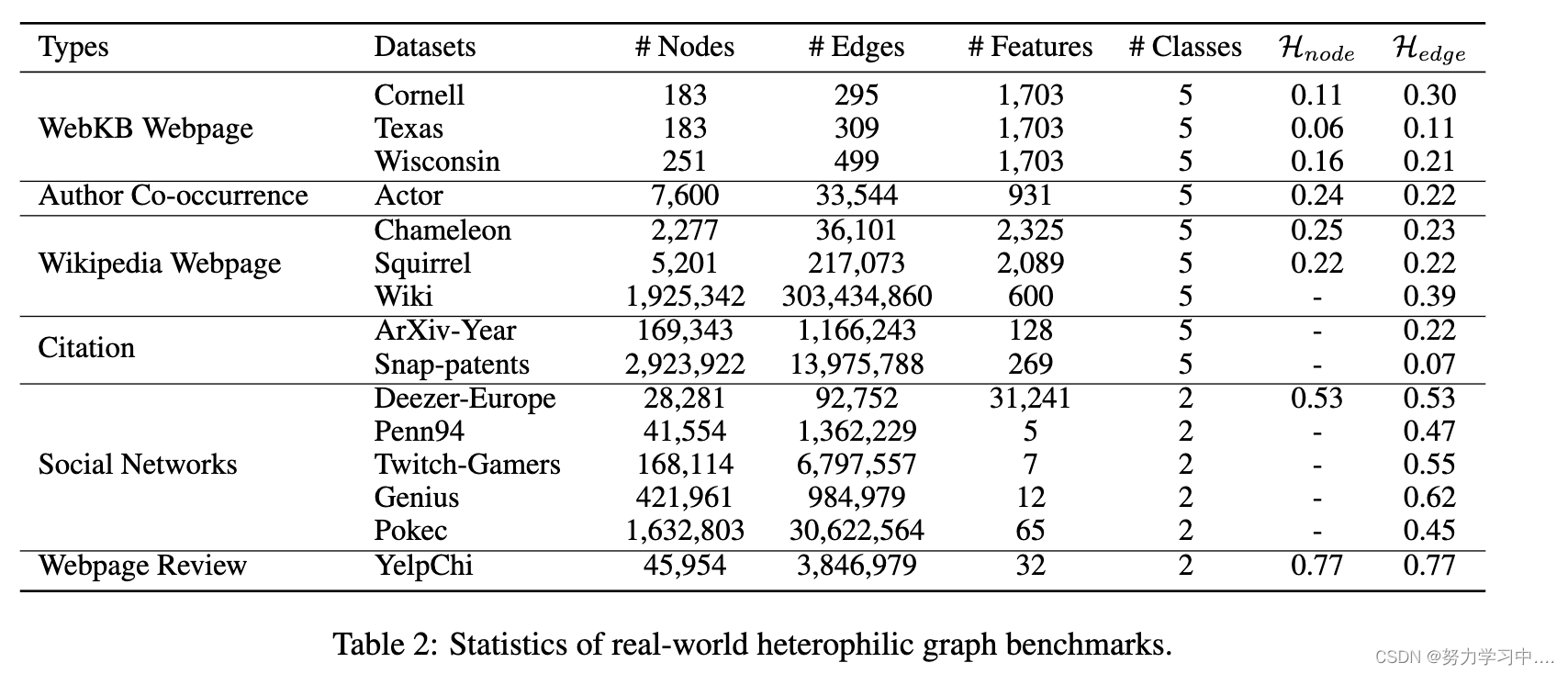
         目前大多数作品都在表2中的前6个数据集上进行实证评估的实验，这些数据集是由工作[Pei等人，2020]最初提出的。具体来说，康奈尔、德克萨斯和威斯康星是WebKB网页数据集[Garc ́a-Plaza等人，2016]中的三个子数据集，其中节点是来自不同大学计算机科学系的网页，边是网页之间的相互链接。

        Chameleon 和 Squirrel 是从 Wikipedia [Rozemberczki et al., 2021] 收集的两个网页数据集，其中节点是特定主题的网页，边是它们之间的超链接。 Actor 是一个演员共现网络 [Tang et al., 2009]，其中节点是演员，边意味着两个演员同时出现在同一个维基百科页面上。

        最近，[Lim et al., 2021a]和[Lim et al., 2021b]收集并发布了一系列来自不同领域的具有较大尺度的新基准数据集。2021b]，包括维基百科网页数据集（Wiki）、两个引文网络数据集（ArXiv-year和Snap-Patents）、五个在线社交网络数据集（Penn94、Pokec、Genius、Deezer-Europe和Twitch-Gamers），以及一个网页酒店和餐厅评论数据集（YelpChi）。可以预见，更多公开可用的异质性基准将被建立，以促进和推动GNN在异质性图上的研究和应用。

5 未来发展方向

        用于异质图的 GNN 在过去几年中发展迅速。 除了当前的研究之外，仍然存在一些值得进一步关注和探索的开放挑战和机遇。 在本节中，我们将讨论以下方向以刺激未来的研究。

        可解释性和稳健性。可解释性和鲁棒性是GNN模型在风险敏感或隐私相关应用领域的两个关键方面，例如健康护理和网络安全。虽然有一些关于同质GNN的可解释性[Ying等人，2019；Luo等人，2020]和鲁棒性[Sun等人，2018]的研究，但如何解释异质GNN的预测以及如何在异亲图上进行对抗性学习仍未被充分探索。异质性使这些任务比同质性更具有挑战性。在可解释性方面，由于大多数近邻节点与自我节点不在同一类别中，从高度异质的图数据中提取可解释的子图要难得多，其中近端和远端拓扑结构都需要被发现和利用。为了提高鲁棒性，简单地添加/检测相似度低的节点对来攻击/防御异质性GNN可能对异质性GNN不起作用，因为由未受干扰的边连接的自我节点本身就与邻居节点有不同的特征。因此，复杂的异质性拓扑结构和语义需要更多的对抗性攻击和防御技术。

        可扩展的异质性GNNs。目前的异质GNN通常在相对较小的图上训练，这极大地限制了它们对大规模数据进行建模和探索更复杂的异亲模式的能力。尽管解决可扩展性的可能方案可以借鉴主流图抽样策略[Chiang等人，2019；Zeng等人，2019]，用于同质GNNs，但如果只抽样小批，异质节点的联系和关系将被低估，特别是当相似和不相似的邻居对学习自我节点表征有不同贡献时。LINKX [Lim et al., 2021a]最近验证了即使是一个简单的基于MLP的模型也能在大规模异质图的小批量训练中胜过GNNs。因此，解决异质图的可扩展性问题需要探索自我邻接节点特征之间的更多关系。此外，在对异质图进行采样时，如何保持固有的异质性不变，仍然是一个开放的问题。

        嗜异质性和过度平滑之间的关系。异质性和过度平滑是限制当前GNNs性能的两个关键方面，其中前者违反了一般的异质性拓扑假设，而后者在性能随着层数的增加而下降时，使大多数GNNs无法深入下去。令人惊讶的是，一些研究表明，可以根据经验利用异质图的GNN来解决过度平滑问题[Bo等人，2021；Liu等人，2021]，反之亦然[Chen等人，2020]。最近的一项工作[Yan等人, 2021]首次尝试解释这两个方面之间的联系，并指出它们可以从统一的理论角度归结为一个共同的原因。然而，在彻底探索和理解异质性和过度平滑之间的关系方面仍然是一个空白。因此，这给研究人员带来了巨大的机会，可以深入研究背后的坚实基础和证明，并进一步共同克服它们。

        综合基准和指标。目前，大多数异质性GNN一般都是在表2中的前6个基准数据集上进行评估，用节点异质性和边异质性来衡量图的异质性程度。首先，这些常用的数据集被认为具有一定的局限性，例如，规模小和协同类，导致异质图的应用范围狭窄。尽管最近发布了大规模的异质图数据集[Lim et al., 2021a]，但还是希望能从更多的真实世界场景中提取异质图数据集，如生物信息学、蛋白质-蛋白质交互和物理过程。同时，除了目前主流的半监督节点分类外，还需要更多的异质图分析任务和应用来进行广泛的异质图数据研究。另外，目前的异质指标只针对嗜血图的节点和边，这大大限制了异质的其他特征的发现，如不平衡的类分布[Lim等人，2021a]和非随机邻居分布[Ma等人，2022]。因此，未来的机会是研究异质性图的基本属性，并提出新的指标来量化这些属性，以进一步加强GNNs的表达能力。