1 基础介绍

在总结粒子滤波之前，还是先从最基本的数学根源问题开始，本质上是一套基于马尔可夫链蒙特卡洛的抽样方法，将这基于MCMC抽样的方法用在机器人状态估计领域，就叫粒子滤波。在《机器人学中的状态估计》一书中是直接从非线性模型开始在贝叶斯框架下描述使用有限数量的随机样本来近似置信度即机器人的后验概率，书中给出了粒子滤波的流程，但没有详细介绍背后的数学来龙去脉。
因此，可以先整理关于抽样方法的数学，在本人之前博客《AI算法-抽样方法》介绍了MCMC的基本思想和技巧，粒子滤波中的MCMC问题主要是研究随机过程的样本容量变化的抽样，也叫序贯抽样。
在蒙特卡洛模拟部分，对模拟的随机误差进行分析，同时讨论如何降低模拟方差的技巧。最后，针对具体的状态估计问题，如何用序贯的MCMC方法解决非线性系统的状态估计, 这些是标准粒子滤波的基本原理性问题。
目前的其他方法都是在标准粒子滤波问题上进行了改进和优化，比如自适应的粒子滤波器，Rao-Blackwellized粒子滤波器。

1.1 隐马尔可夫链

	之前讨论马尔可夫链满足细致平衡条件，还有一条性质是无后效性，即过程的下一状态只与当前状态有关，与以前状态无关。下面会讨论这条性质如何简化模型。

1.1.1 马尔可夫链性质

(1) 随机过程的状态序列为：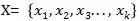

将随机过程的概率分布f(X),表示为条件概率分布形式：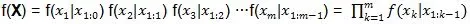

上述形式称为顺序随机过程。顺序随机过程的概率分布写成多个条件概率分布乘积的形式，可以说明两点：
序贯抽样的基本框架是序贯地构造条件概率分布f(X)， 序贯地从条件概率分布f(X)抽样
顺序随机过程的下一个状态不仅与当前状态有关，还与之前的所有状态有关

(2) 马尔可夫链的无后效性
即将来时刻k+1的状态只与当前时刻k的状态有关，与以前任何时刻的状态都无关，用公式表示为：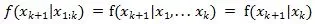

因此马尔可夫链的条件概率分布f(X)可以简化为: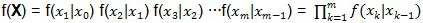

在粒子滤波器权重推导中，也将不使用任何后遗症来简化推导过程。

(3) 隐马尔可夫随机过程

上图是一个简单的马尔科夫模型，状态对观察者是直接可见的，所以状态转移概率是唯一的参数。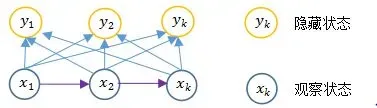

上图是隐马尔可夫模型，它的状态不能直接观察到，但能通过观测向量(黄色的圈圈)序列观察到，每个观测向量都是通过某些概率密度分布表现为各种状态(可以称为隐藏状态)，每一个观测向量是由一个具有相应概率密度分布的状态序列产生。即推测的东西(状态X序列)不能直接观测到，而是根据另一种我们可见的这种观测的东西(状态Y序列)去推算我们想知道的信息。
隐马尔科夫模型的随机过程是马尔科夫随机过程的一种特殊情况，也具备相同的性质，包括无后效性。而机器人中的状态估计问题(粒子滤波) 被表示为动态空间模型,动态空间模型是一种隐马尔科夫随机过程，这样就可以使用隐马尔科夫模型(HMM)的性质。

1.1.2 动态空间模型

(1)动态空间模型，包括过程模型和观测模型，分别由状态方程和观测方程描述。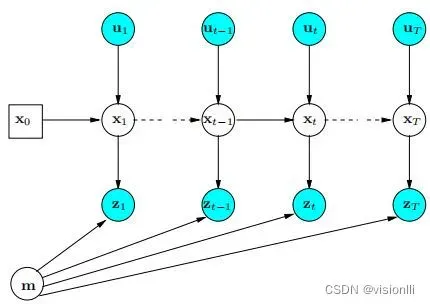

根据上图可知，进程的下一个状态只与当前状态有关，与前一个状态无关。
观察状态X(t+1) 只与X(t) 有关,与X(1:t-1) 无关,状态X(t)接收过程激励U(t)。
隐藏状态Z(t) 只与X(t)有关

(2)动态空间模型的动态方程，是对动态系统的描述，而状态方程和观测方程构成动态方程，根据具体的系统类型有不同的形式,主要包括线性系统

和非线性系统的动力学方程：

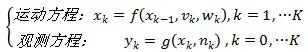
根据动态空间模型， 由过程输入V(或者空间模型图的U)，过程噪声w, 观测值Y(或者空间模型图的Z)和观测噪声n，求解状态X的估计值， 就是状态估计问题。动态空间方程会在后面推导中使用。

1.2 蒙特卡洛模拟

大数定律和概率论的中心极限定理是蒙特卡罗方法的数学基础。蒙特卡洛方法有两个重要特点：一是随机变量或随机
该过程及其概率分布是一个随机抽样问题；另一个是统计量，这是一个统计估计问题，即样本推断总体。

(1 )先看网上比较经典的蒙特卡洛求面积例子：
初学者都能看懂的蒙特卡洛方法以及python实现

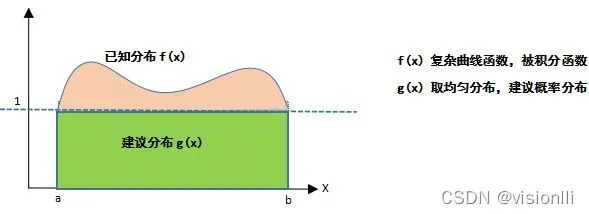
假设要计算的积分问题是：

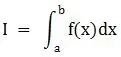
根据变量代入的思想，如果不能直接得到积分函数，可以先从提出的概率分布中采样，然后求解要估计的问题：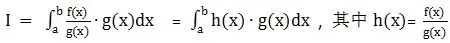

经过以上转化h(x)和g(x) 分别是什么东西了 ？ 在统计学上，分别表示：
(A)g(x) 就是关于x的建议的概率分布函数，作为样本的采样分布。可以自己选择，上面选择的均匀分布。从g(x) 中采样生成样本点：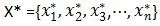

(B)h(x) 表示样本对应的统计量, 样本是进行统计推断的依据，在应用时，往往不是直接使用样本本身，而是针对不同的指标构造样本的适当函数（即统计量），是对样本的一个量化指标，利用统计量进行统计推断。例如统计量的均值和方差。注意不是样本的均值和方差。由统计量的算术平均值得到统计量的估计值， 作为所要求解问题的近似估计值: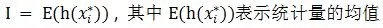

蒙特卡洛算法流程：随机抽样产生样本值，确定并选择统计量，从统计量的算术平均值中得到统计量的估计值，作为待解决问题的近似估计值。

那么蒙特卡洛模拟在粒子滤波中起什么作用呢？

1.3 序贯重要采样

在贝叶斯框架下，经过贝叶斯变换后，被积函数的形式多为积的形式：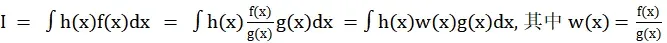

此时的g(x) 是建议的概率分布，在SIS中或叫重要分布，从建议分布g(x)中进行重要性采样，样本值：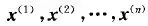

h(x)w(x) 任然是统计量，w(x) 成为重要性权重，权重描述f(x)和g(x)在某个样本点的接近程度。
最后，根据统计量估计，将积分运算换成统计量的均值：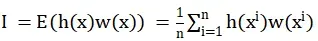

以上分析直是解决了SIS中的重要采样，没有解决序贯的问题，怎么构造序贯了？在采样方法中提到了，序贯采样时把序贯随机过程概率分布写成多个条件概率分布乘积的形式，表明序贯抽样的基本框架是序贯地构造条件概率分布，与1.1节形式一样，因此我们的重要概率分布g(x)：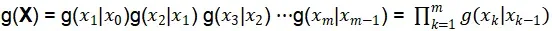

已知分布f(x) 写成多个条件概率分布乘积的形式: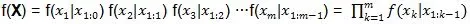

权重可以表示为：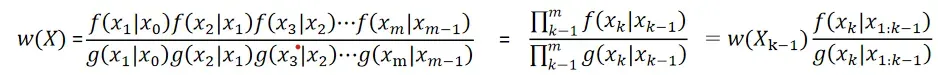

上述过程构成了顺序重要性抽样的主要框架，但不能在实际中使用，需要进一步改进。主要问题是：
序贯重要抽样方法需要进行迭代计算，计算时间消耗很大，更为严重的是由于使用重要抽样技巧而出现样本退化现象。随着迭代次数的增加、权重值计算量不断地增加权重值的方差也不断地增大。极少数样本的权重越来越大，大多数样本的权重越来越小.样本权重将越来越集中到少数几个样本上，除了少数儿个样本外其余样本权重几乎趋于零，因此绝大多数样本权重很快变为零，缺失样本多样性。
如何解决这个问题呢？使用样本拆分和重采样技术：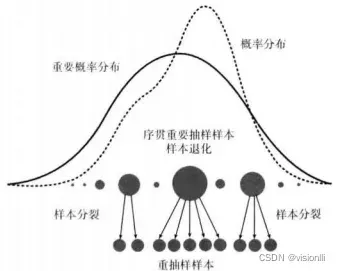

重抽样是淘汰权重小的样本，繁殖权重大的样本，将权重大的样本进行分裂，一个权重大的样本分裂成几个权重相同的小样本，从而抑制退化现象，这里可以说是粒子滤波的精髓，体现了”优胜劣汰”的思想，大量繁殖权重高的粒子，淘汰权重值低的粒子。我们知道重要性权值是对相应的样本值X*的质量好坏的度量，因此重采用算法的问题模型是给定样本集合与权重有序对：

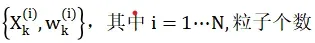
经过采样算法，粒子总数保持不变，权重大的粒子分解为多个粒子，权重小的粒子被抛弃，重采用后粒子权重相同，均为1/N: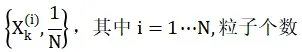

重用主要解决样本统计量方差大的问题。我们知道蒙特卡罗模拟的统计误差定义为：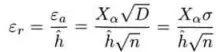

重采样样本的权重都相同，减少了模拟的方差。蒙特卡罗方法的效率与统计量的方差和每次模拟的时间成反比。在降低方差的同时，也增加了算法的仿真时间，提高了效率。

除了重采样（样本拆分），还有什么技巧可以减少方差吗？目前主要有两种技术：
(1)只改变概率分布f(x)： 重要抽样是把概率分布改变为重要概率分布，分层抽样是把整层概率分布改为分层概率分布。
(2)只改变统计量h(x)： 例如，控制变量、对偶随机变量、公共随机数和样本分裂(重采样)。
(3)同时改变概率分布和统计量。

后面会分析AMCL使用了种技巧来降低方差技巧。

重采样就完美了吗？不必要。重采样后，权重较大的样本被重复复制，所有样本都会收敛到一个点，严格的样本会失去统计独立性。幸运的是，粒子滤波问题的下一个状态只与当前状态有关，与前一个状态无关，在统计上是独立的。马尔可夫结构的频繁重采样不会导致严重的样本耗尽问题。

1.4 贝叶斯推断

1.4.1 贝叶斯公式

在粒子滤波或者状态估计里面，贝叶斯干了啥了，实际基于贝叶斯估计框架因为含有高维积分，很难求解，不具备解决实际问题的意义，但是贝叶斯提供了一套理论框架。状态变量x的先验概率分布为f(x), 观测变量y的 概率分布为f(y|x) , 由贝叶斯定理得到状态变量x的后验概率分布为f(x|y)：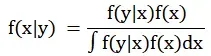

这里没有具体展开。可以参考《概率机器人》的贝叶斯过滤章节。下面的递归权重需要用到两个关键公式，为了方便，用简单的随机变量表示：
（1）贝叶斯公式：f(A|B)=f(B|A)*f(A)/f(B)
（2）联合概率 = 条件概率 * 边缘概率：f(A,B) = f(A|B) * f(B)
（3）条件概率分布变换规则:f(a,b|c) = f(a|b,c) * f(b|c)，这个公式在后验概率推导中很关键。

1.4.2 后验概率分布

在粒子滤波中，采用一个PDF来刻画当前状态的估计问题，即后验概率分布f(X|Y) ，状态X的下标是多少了？有些书中下标是k,有些是0:k, 因为对当前状态的估计需要考虑历史所有状态的情况，正规的下标是采用0:k，表明后验概率分布是对过去所有时刻状态的后验。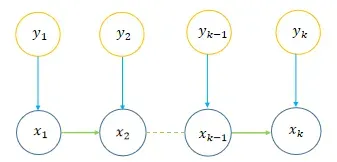

后验概率分布形式在上面定义为：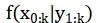

2 粒子滤波

基于以上的基础，蒙特卡罗模拟是要求0:k的状态，通过状态样本的统计量，构造蒙特卡罗状态估计问题模型，将统计量的估计值 作为所要求解问题的近似值。
(1) 待求解的问题统计量设为：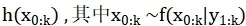

（2) 构造蒙特卡罗积分:

（3) 选取建议(重要)概率分布:

(4) 对(3)中积分展开，蒙特卡洛样本值统计量估计(估计后验概率分布);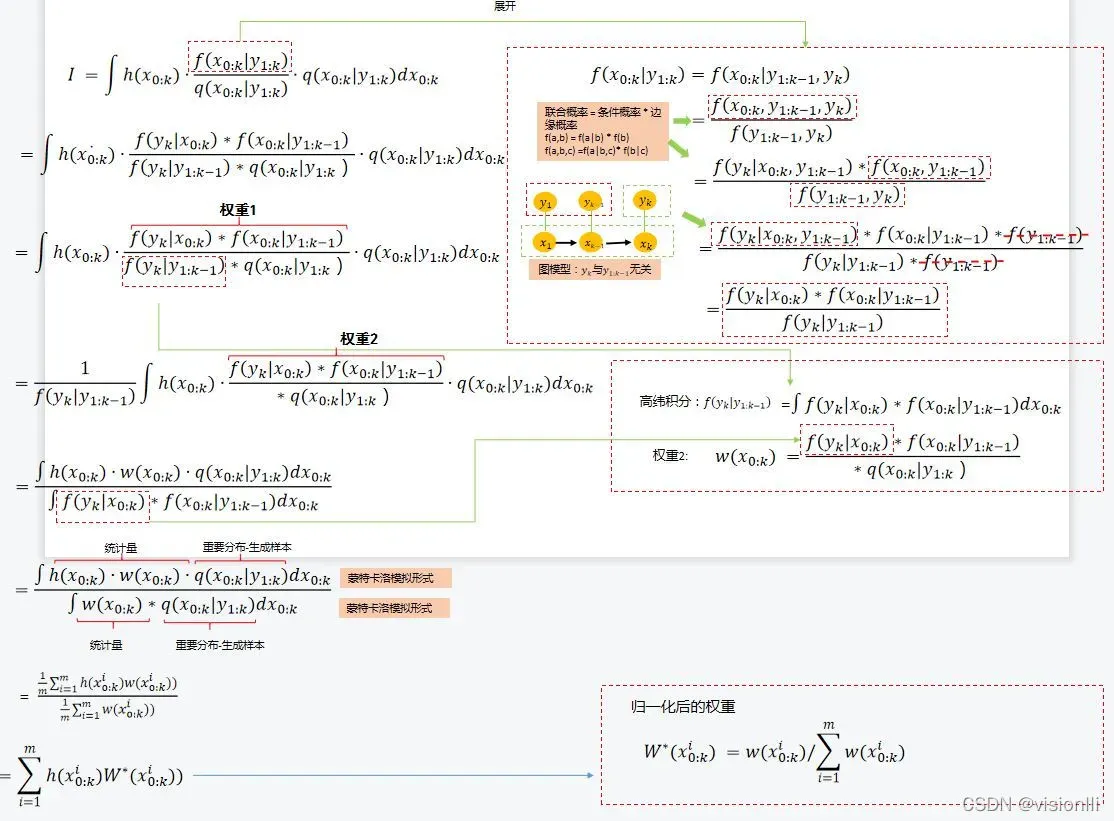

（5） 序贯递推权重，根据(4) 知道权重2作为最终的样本点权重，可以继续展开权重2，目的是写出与上一时刻的递推关系：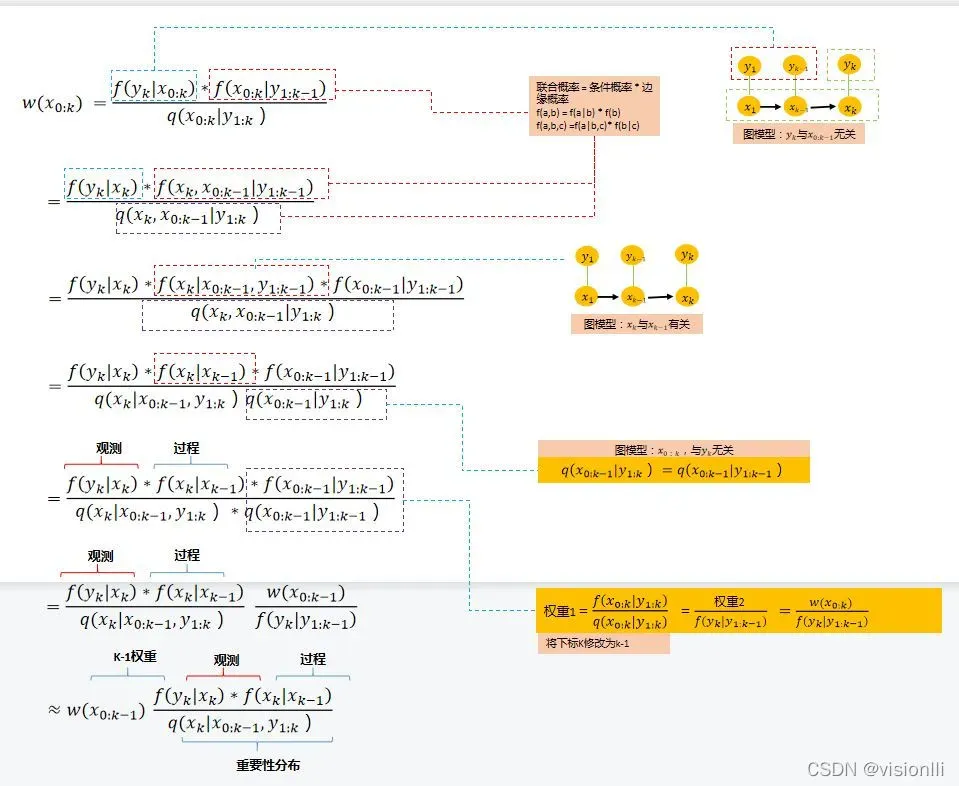

初始权重：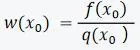

（6）重要性分布具体选择：
在标准粒子滤波器中：选择重要性分布作为过程分布（prior distribution）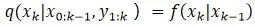

那么权重递归可以进一步简化为：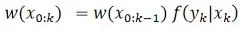

总结：先k-1时刻从重要性分布(先验分布)采样，生成k时刻的样本， 然后通过K时刻的观测，修正k-1时刻的粒子权重。
还有个问题f(y|x)在统计学上叫观测似然，具体是什么形式了。

2.1 标准粒子滤波

2.2 AMCL滤波

2.2.1 似然模型f(y|x)

统计学中，似然函数是一种关于统计模型参数的函数。给定输出样本x时, 用样本估计y。f(y|x)表示在状态x出现的条件下，测量y出现的概率。博客[2] 将f(y|x)等价于一个高斯分布，并不具备实际的应用意义。

在机器人导航定位中，针对于距离传感器来说，其在定位过程中的作用，主要任务是解决 f(y|x)，也就是在给定机器人位置x之后，如何评估获得已知观测信息 y的概率的问题。如何测量这个概率，就是传感器模型要解决的问题。

在机器人状态估计模型中f(y|x)，具体形式表示为：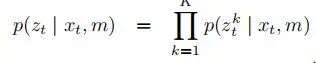

将观测似然写成各个观测值乘积的形式，即在给定机器人位置之后，其所有的观测都是独立的。AMCL中提供了两种模型：
(1) 波束模型（Beam model）
传感器模型为了准确描述测量（measurement），重点是要定义各种测量误差并且量化这些误差。
参考书籍《PROBABILISTIC ROBOTICS》

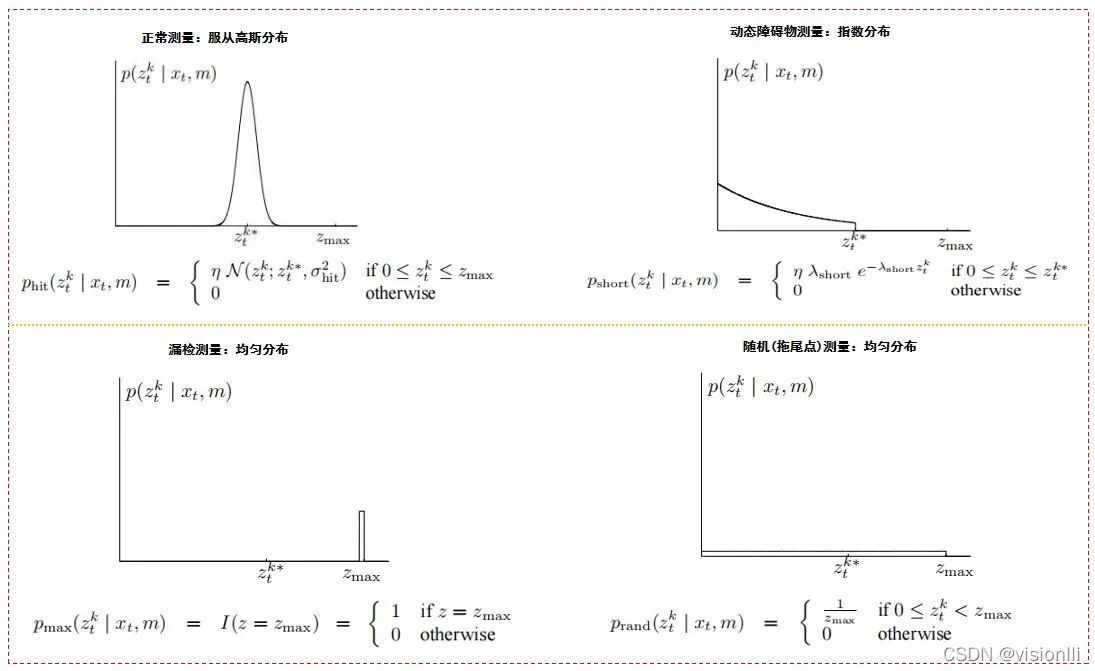
我们需要的p(z|x,m)（或f(y|x)）如何将这四类测量都考虑进去了，怎么分配四类测量的比列？这里采用权重表示，形式如下：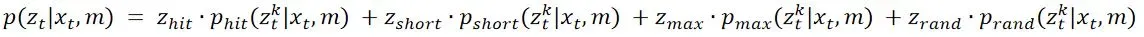

其中权重满足：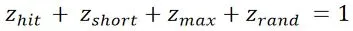

写成矩阵形式：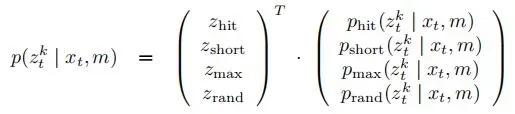

(2) 似然域（Likelihood Field）

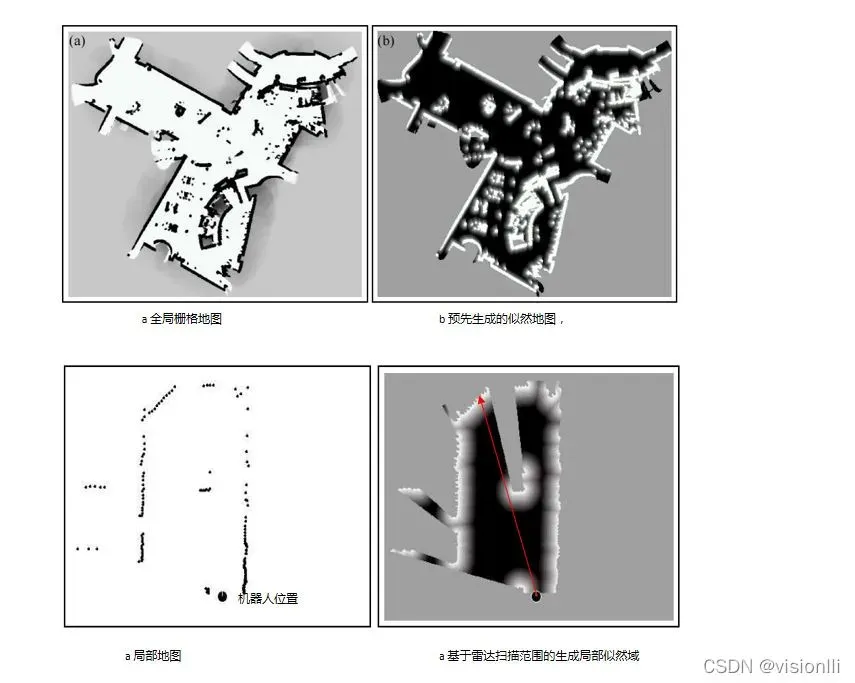
似然域是单色（黑、白、灰）的灰度图像。颜色越白，检测区域内障碍物的可能性就越大。相反，颜色越深，可能性越小。

定量噪声是指障碍物的测量位置不能与地图上显示的障碍物位置完全匹配。这种噪声可以用两者之间的欧几里得距离作为地图上距离测量终点最近的障碍物中心进行高斯分布拟合。也就是说，该模型中概率分布的求解只关心测量已知障碍物的末端，而不关心所有光束的数学和物理性质。在似然域模型中只需要考虑以下三个分布：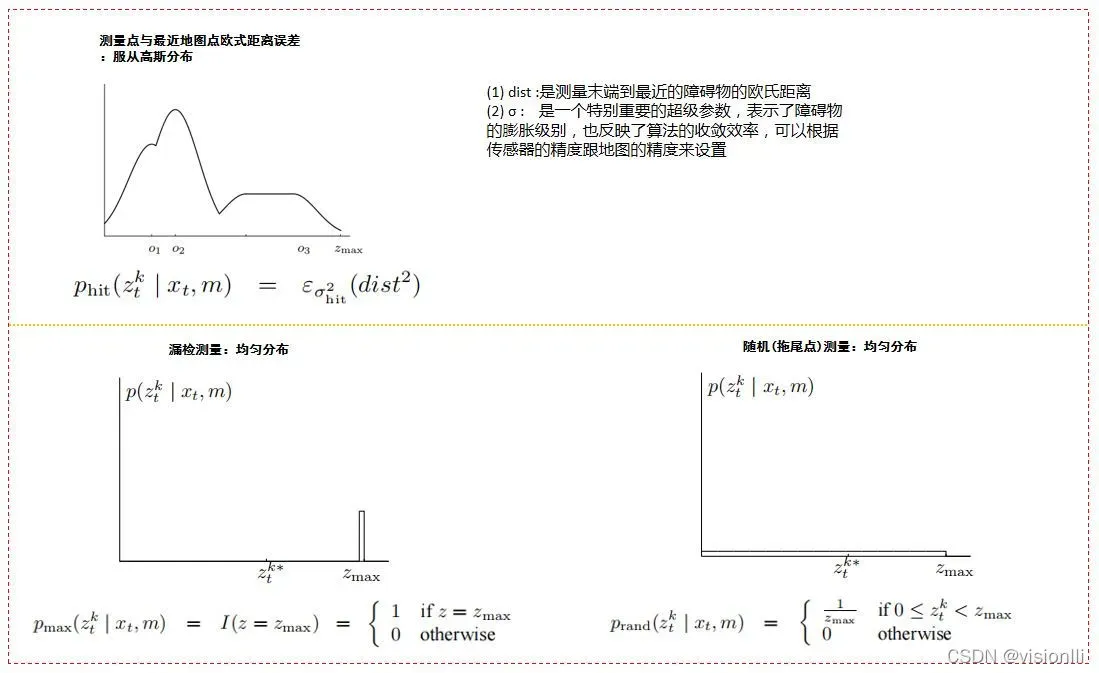

怎么根据似然域确定观测似然的分量值了Zt ，从机器人上的测距仪的一条扫描线开始，依次的从机器人出发、沿虚线向远处依次检测的过程，判断曲线属于那种误差分布，并且计算相应的概率值，然后累加。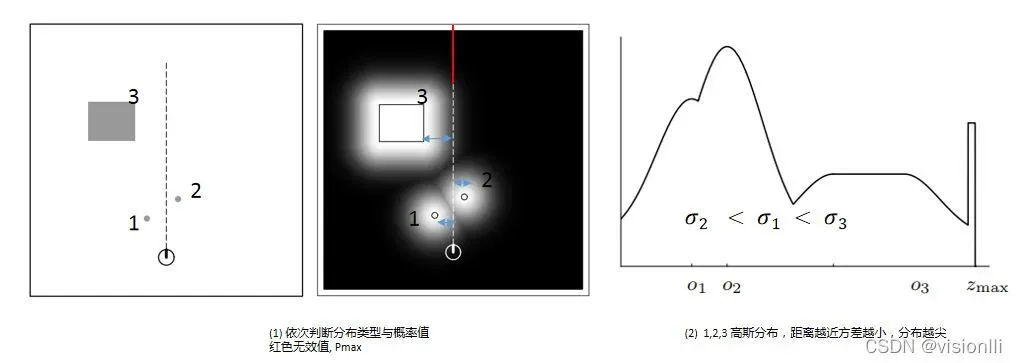

我们需要的**p(z|x,m)**形式如下：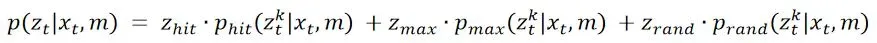

其中权重满足：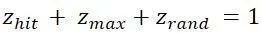

综上所述，计算观察似然度的算法流程如下：

以上是AMCL的观测似然模型，相对标准粒子滤波，还有什么不同的了？

2.2.2 KLD采样

(1) 在线改变粒子数
标准粒子滤波器样本总数保持不变，每次模拟使用预先给定的固定样本数，
AMCL其主要的不同地方是自适应的在线改变粒子数量，其背后的目的是提高蒙特卡洛模拟的效率同时可以兼顾精度，在收敛到平稳分布前，通过增加粒子数量,保证样本统计量具备较小的方差，当达到平稳后，可以适当的减小粒子数，此时的粒子的目标分布更接近真正的分布,减小适当的减小粒子数可以蒙特卡洛模拟的效率，减小内存消耗。

(2) 相对熵
先看KLD是啥？是不是粒子滤波特有的？KLD来自信息论，要了解KLD前需要准备一些基础知识：
相对熵（relative entropy），又被称为Kullback-Leibler散度（Kullback-Leibler pergence）或信息散度（information pergence），是两个概率分布（probability distribution）间差异的非对称性度量 。在信息理论中，相对熵等价于两个概率分布的信息熵（Shannon entropy）的差值。 KLD采样背后的思想就是根据基于采样近似质量的统计界限来确定粒子数量。 更特殊的，在粒子滤波器的每次迭代过程中，KLD采样以概率1−σ来确定样本数量，真实的后验概率与基于采样的近似分布之间的差异小于ε。

先看基本定义1： 相对熵
设P(x)和Q(x)是随机变量x上的两个概率分布，则在离散和连续随机变量的情形下，相对熵的定义分别为: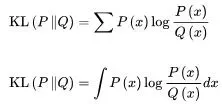

再看基本定义2：卡方分布
Baidu Chi-square distribution

让我们看看如何使用它：
继续上面的过程，我们知道标准粒子滤波器已经初始化，重要性采样，重采样得到一组加权样本集。接下来，我们知道如何使用样本集的估计分布来判断样本与真实概率分布的差异。距离。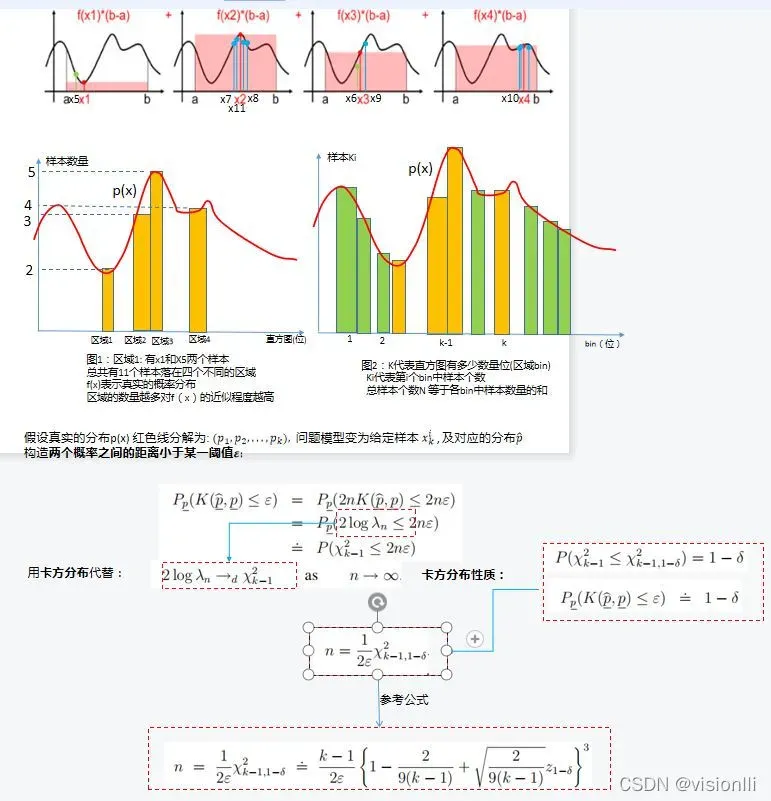

KLD中主要的思想就是用卡方分布去近似计算估计概率分布和真实概率分布之间的距离。下面直接看论文KLD论文中：

2.2.2 算法流程

具体来分析一下KLD是怎么体现在线改变粒子数的过程：

最后, 其他粒子滤波算法都是在标准粒子滤波算法上的改进，无外乎改进概率分布，统计特性(包括重采样)，衍生出了不同的算法除了AMCL还有Rao-Blackwellized粒子滤波器，又在哪一步做了改进，与卡尔曼有什么关系, gmapping是怎么用的？**
基于以上基本流程，后面会分专文分析介绍。

参考

[1]: https://www.cnblogs.com/pinard/p/6638955.html
[2] https://blog.csdn.net/guo1988kui/article/details/82778293
[3] https://zhuanlan.zhihu.com/p/126199044
[4]: 《蒙特卡罗方法理论和应用》康崇禄
[5]: 《粒子滤波算法及其应用》朱志军
[6] https://blog.csdn.net/weixin_42530239/article/details/96501814