1.基础

见《数字图像处理第四版》P137-P209

1.1傅里叶变换Fourier Transform

Fourier Transform由法国的一位数学家和物理学家Jean-Baptiste Joseph Fourier (1768-1830)提出，主要包括适用于周期函数的傅里叶级数(Fourier Serier)和应用于非周期函数(曲线下面积有限)的傅里叶变换。

• 傅里叶级数
  傅里叶级数意味着周期为的连续变量的周期信号可以表示为正弦函数和余弦函数之和乘以适当的系数。
  借助欧拉公式和欧拉恒等变换，

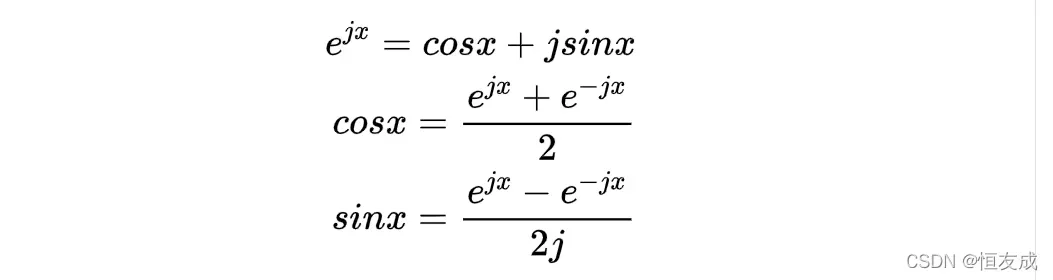
傅里叶级数可以用复指数的形式表示，形式为，

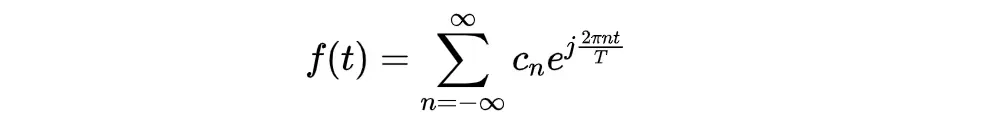
其中，系数可表示为：、
从傅里叶级数的的公式可以看出，周期函数被分解成了使用不同频率，幅度，相角的正弦和/或余弦函数表示的形式。能够将信号从时域在频域上展开来进行分析。这正是傅里叶变换的意义，关于其形象化的描述可参考

• 连续函数的傅里叶变换
  非周期函数可以看成是一个周期无限大的函数。参照傅里叶级数中的，其频率与系数大小的关系，即傅里叶变换，可表示为：
  

1.2卷积定理

连续变量t的两个连续函数和的卷积的定义为：

其中，表示对卷积核函数旋转180度，是一个函数滑过另一个函数的位移，是积分虚拟变量。上式的傅里叶变换表示为：

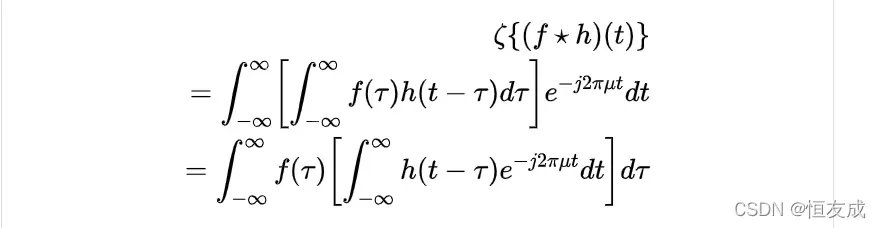
式中方括号内是的傅里叶变换，,是的傅里叶变换，式（5）可表示为：
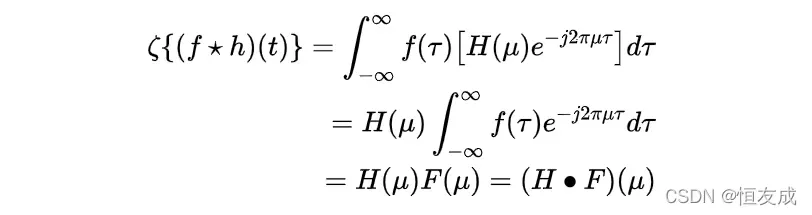其中表示乘法，表示傅里叶变换。

从上式可以看出，两个函数在空间域的卷积的傅里叶变换等于两个函数在频域的傅里叶变换的乘积。反之，如果频域有两次傅里叶变换的乘积，则可以通过计算傅里叶逆变换得到空间域的卷积。综上所述，卷积定理可以表示为：

1.3冲激函数及其取样性质

连续变量在处的单位冲量表示为，表示为：

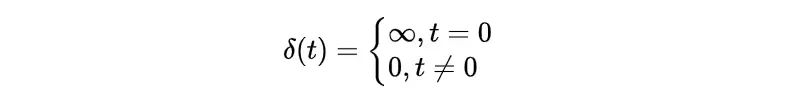
脉冲函数满足以下性质：

• 满足身份：
• 采样属性：，采样属性刚好在脉冲位置处得到的值。

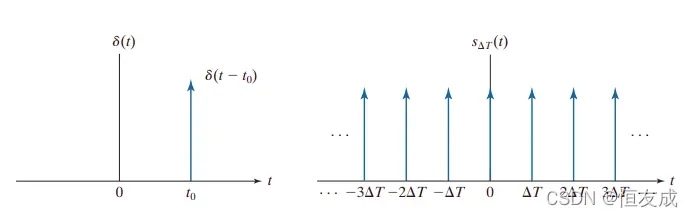
实际采样时，需要使用一系列脉冲信号，以为间隔进行采样，这样可以定义脉冲串：

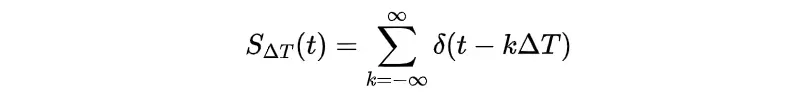
在上面，被解释为一个连续的时间变量。对于离散变量，冲激函数定义为：

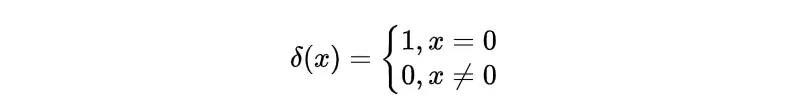
满足的性质等价于：

• 身份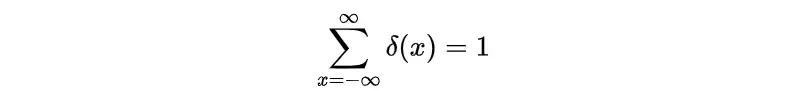：– 采样属性：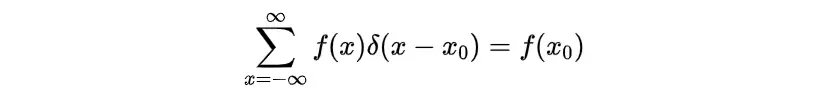

1.4冲激和冲激串的傅里叶变换

根据连续单变量函数傅里叶变换的定义，函数的傅里叶变换可表示为：

在处，脉冲的傅里叶变换为：

为了获得离散信号，通常需要使用周期性脉冲序列进行采样。因此，在推导离散信号的傅里叶变换时，需要先得到周期脉冲序列的傅里叶变换。

首先，由上面的定义的傅立叶变换和反变换可知，若函数有傅立叶变换,则函数的傅里叶变换为,由此性质,冲激的傅立叶变换为，则的傅里叶变换为。记,则的傅立叶变换为,对于冲激函数，除外，都为0，因此，也即。

由1.3知是周期为的周期函数，其傅立叶级数表示为：

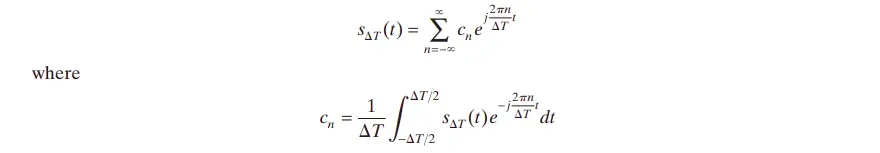
周期对的积分只包括原点的冲量，所以可以表示为：

那么，傅里叶级数可以表示为：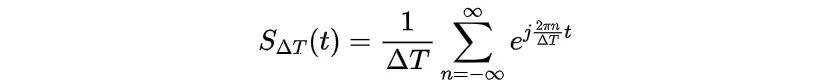
结合以上，则

组合和的傅里叶变换等于各分量的傅里叶变换之和，则周期脉冲串的傅里叶变换为

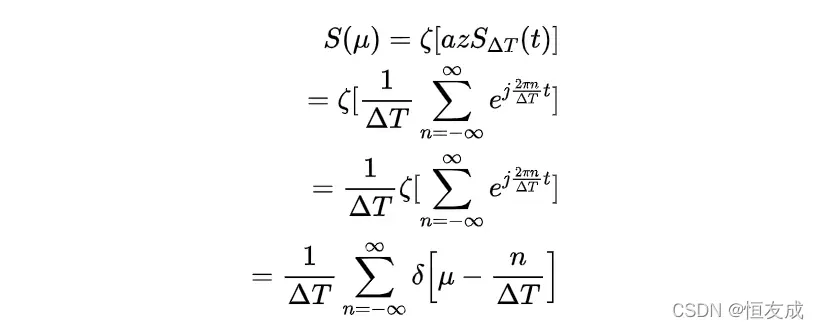由上式可知，周期为的脉冲串的傅里叶变换仍是脉冲串，其周期为，其周期成反比。

1.5取样后函数的傅里叶变换和取样定理

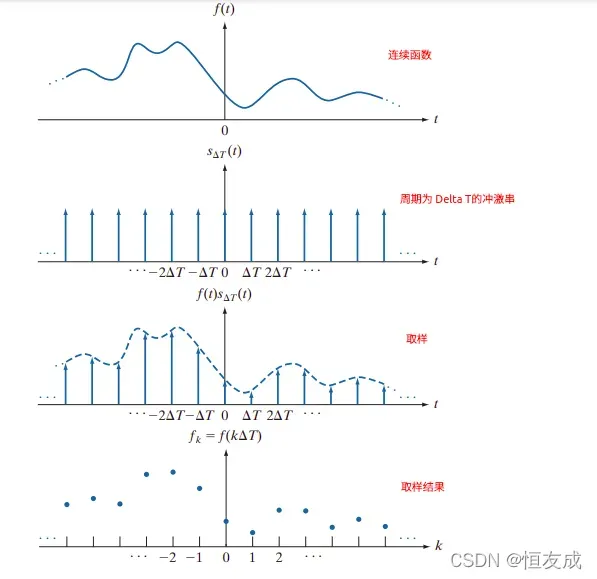
使用脉冲序列采样的过程如上图所示，其数学表达式为：

表示采样后的函数。采样后，采样序列中任意一个样本的值由下式给出：

采样函数的傅里叶变换表示：
表示连续函数函数的傅里叶变换，采样函数和与脉冲串的乘积。根据卷积定理，空间域中两个函数的乘积的傅里叶变换是频域中两个变换的卷积。因此，的傅里叶变换可以表示为：

由以上推导可知，脉冲序列的傅里叶变换为：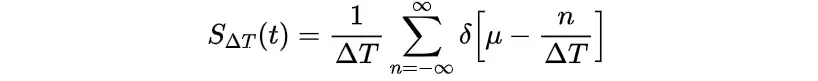

根据一维卷积的定义，和的卷积可以表示为：

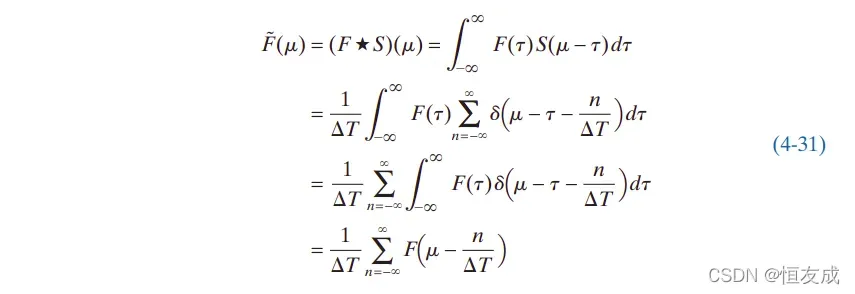
由以上推导可知，采样函数的傅里叶变换是原函数傅里叶变换的无限循环复制序列。考虑带限函数的傅里叶变换示意图：

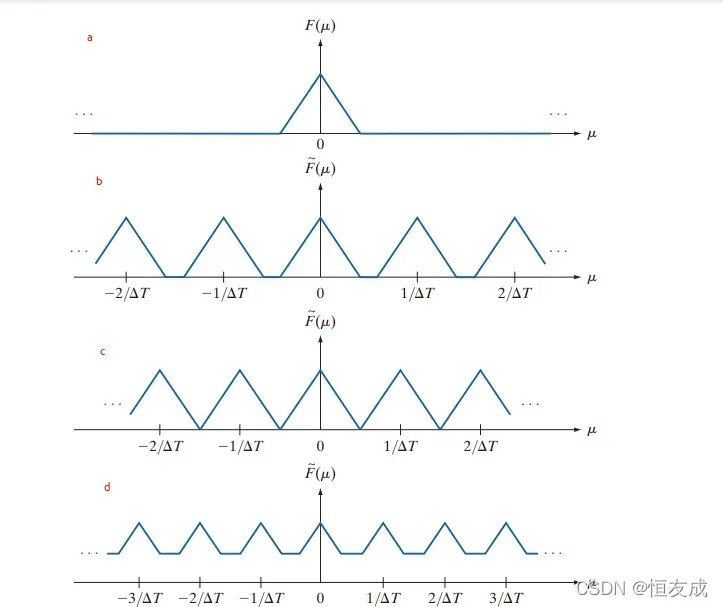
上图中，图a是函数的傅里叶变换,图b是函数的傅里叶变换，是取样函数的取样率，从上图可以看到取样率要高到足以在各个周期之间提供有效的间隔，以保持的完整性。图c和图d分别对应的是临界取样和欠取样。

对于以原点为中心的有限区间以外的频率值，傅里叶变换为零的函数称为带限函数。从上图可以看出，当很大时，会重叠，完整的不能与分开，即无法通过傅里叶逆变换恢复原始信号。因此，为了恢复原始信号，必须提高采样频率，如下图所示：

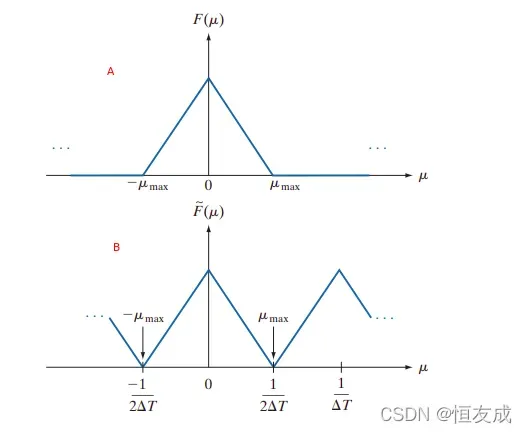
当时可以保证足够的间隔：，该式表明，如果以超过函数最高频率2倍的取样率来得到样本，那么连续带限函数就能由其样本集合复原，该结论即取样定理。

1.6由取样后的数据复原函数

定义函数为：
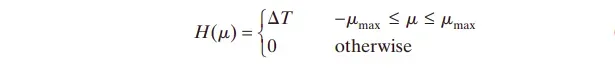则为：，得到后，可通过傅里叶逆变换恢复：

从我们可以得到：

即频域中函数的处理相当于空间域中的卷积。

2.离散傅里叶变换（Discrete Fourier Transform)

2.1一维离散傅里叶变换

前面讨论采样定理时，发现了采样函数的傅里叶变换与原函数的傅里叶变换之间的关系，但没有给出的表达式。定义要求：

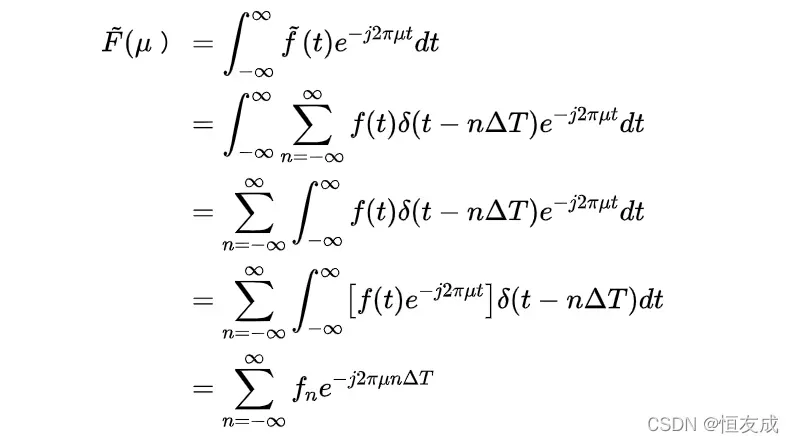
由与的关系，可知，是周期为的无限周期连续函数，因此表征只需要一个周期。假设从到的一个周期内等间隔的取的M个样本，在如下频率处取样可实现：把代入上面的公式中可得的表达式为:

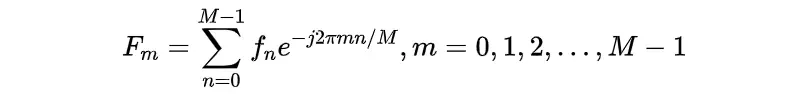
已知一个由f(t)的M个样本组成的集合时,上式给出了一个与输入样本集合的离散傅里叶变换相对应的M个复值集合。反之，求得时也可由傅里叶反变换求得

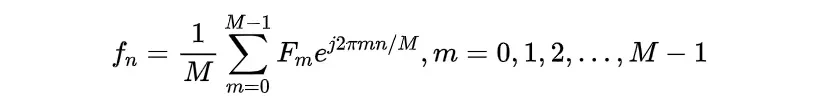在图像中，和通常用于表示图像坐标，和用于表示频率变量。这些变量被理解为整数，上面的傅里叶变换对可以表示为：

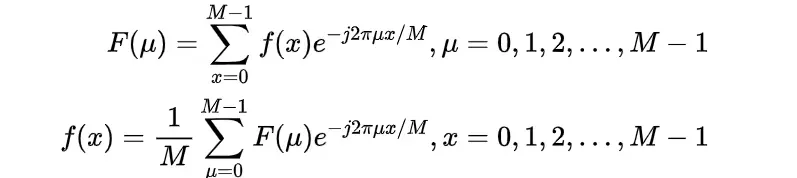
2.2二维函数的傅里叶变换：

将前面的概念扩展到两个维度。

二维脉冲函数：

二维脉冲函数的采样性质：

二维连续函数的傅里叶变换对：

和

二维脉冲序列（二维采样函数）：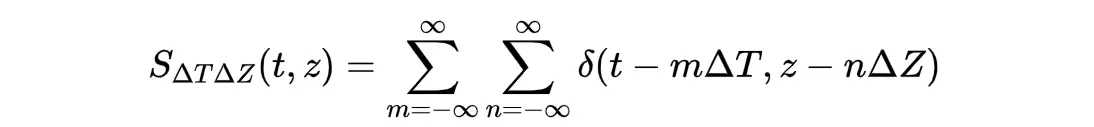

二维采样定理：

2D 信号的混叠：

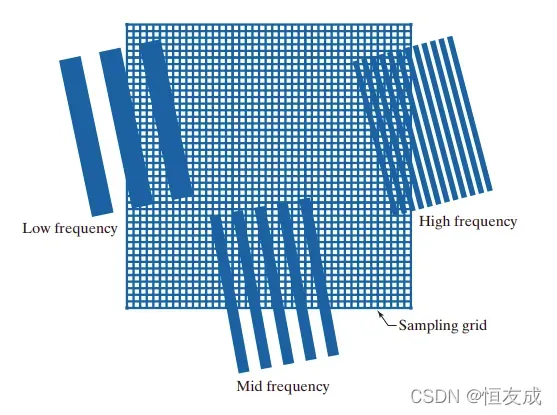二维离散傅里叶变换对：

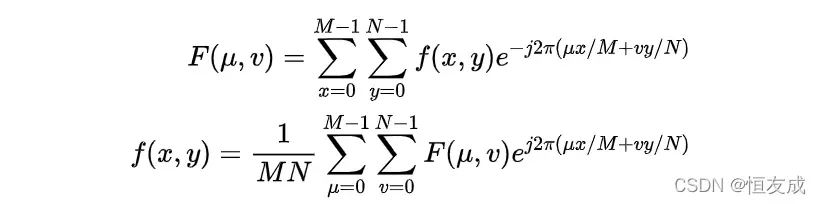
二维离散傅里叶变换的平移旋转和周期性：

从定义可以得到：

• 潘：
  
  用所示的指数项乘以将使DFT的原点移动到处，用负指数乘以将使的原点移动到点处。平移不影响的幅度
• 回转：
  使用极坐标：,则有如下变换对：$f(r,\theta+\theta_0)\Leftrightarrow F(\omega, \varphi + \theta_0)\theta_0F(\mu,v)F(\mu,v)f(x,y)$也旋转相同的角度。
• 定期：
  在同一维下，二维离散傅里叶变换及其逆变换在和方向上是无限周期性的，即：
  
  和
  
  从第一部分的分析，可发现，区间0到M-1上的变换数据由在点处相遇的两个半周期组成，可以发现该周期内较第部分的出现在较高的频率处，不便于分析和滤波。根据上述的平移性质，
  
  该式将把数据的原点平移到,若另,则指数项变为,因为x是整数，故根据欧拉公式，其可表示为,代入上式可得：
  
  如下所示。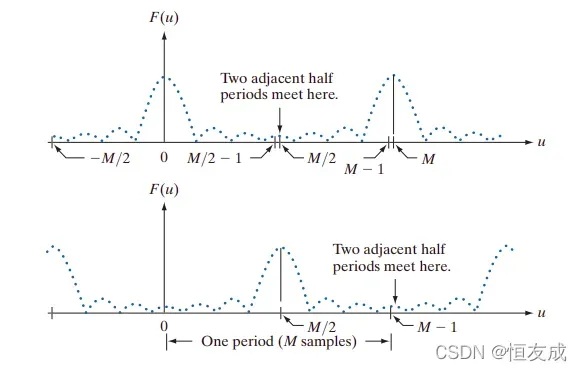
  对于二维情况，可以表示为：
  

频谱、相位频谱和功率频谱：

从前面的分析可知，二维DFT通常是复函数，用极坐标形式表示为：

傅里叶光谱：

相谱：

功率谱：

一张图像的光谱示意图如下：

图A是原图像，图B是直接对原图像进行傅里叶变换得到的频谱，可以看到四个角较亮，但因为其值分散在四个角落，因此很难观察，使用前述的变换，对原函数乘以将其变换的中心移动到图像的中心可得图C，更便于观察分析。图D是对频谱值取对数后的结果。

2.2二维离散卷积定理

将一维离散卷积定理扩展到两个变量，我们得到：

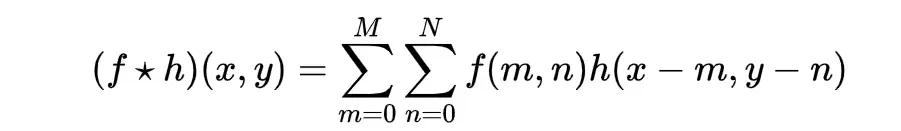二维卷积定理可以表示为：

使用卷积定理时的问题：

如果使用DFT和卷积定理来求得如下图左列相同的卷积结果时，需考虑DFT表达式中固有的周期性。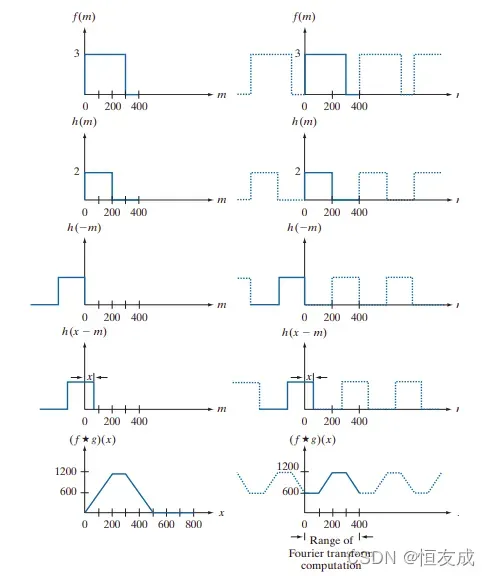

上图中左列，是根据定义使用尺寸为400的卷积核对尺寸为400的原信号进行卷积，先对卷积核函数旋转180度，再依次滑过原信号，得到图左列最后所示的卷积结果。

若使用卷积定理，则f,h都具有周期性，若根据卷积定理，先计算f和h的DFT，然后让这个变换相乘，再计算傅里叶反变换，将得到如上图右侧所示的结果，显然如此计算的卷积结果是不对的。

交叠错误很容易解决。考虑f(x)和h(x),他们分别由A个样本和B个样本组成，可证明，若在这两个函数中填充零，使他们长度P相同，则选择

可以避免重叠错误。

令和分别表示大小为像素和像素的图像阵列.它们循环卷积中的交叠错误可通过对这两个函数填充零来避免，

其中，、

填充零后图像大小为,若两个阵列大小相同，都为,则要求和.DFT算法执行偶数大小的阵列时速度较快，因此通常选择满足上述公式的最小偶整数作为P和Q的值，若两个阵列相同，则和

3.频率域滤波步骤

• 1）一幅大小为的输入图像,由前述公式得到填充零后的尺寸P=2M和Q=2N
• 2)使用零填充，镜像填充或者复制填充，形成大小为的填充后的图像
• 3)根据前述二维傅里叶变换的平移性质，将乘以，使傅里叶变换位于大小的频率矩形的中心
• 4）计算步骤3得到的图像的DFT，即
• 5）建一个实对称滤波器传递函数,其大小为,中心在处
• 6）采用对应像素相乘得到,即和
• 7）计算的IDFT得到滤波后的图像(大小为PXQ)：
• 8）最后，从的左上象限提取一个大小为的区域，得到与输入图像大小相同的滤波结果

4.OpenCV API

• int cv::getOptimalDFTSize ( int vecsize )
  在进行傅里叶变换时，需要对原始图像进行扩展以提高处理速度。这种方法正是为了获得满足最优处理速度的最小扩展。
• void cv::copyMakeBorder ( InputArray src, OutputArray dst, int top, int bottom, int left, int right, int borderType, const Scalar & value = Scalar() )对图像进行扩充，可设置上下左右的扩充大小和类型
• void cv::merge ( const Mat * mv, size_t count, OutputArray dst )将数组mv合并成count channel的dst，与split刚好相反
• void cv::dft ( InputArray src, OutputArray dst, int flags = 0, int nonzeroRows = 0 )执行1d或2d离散傅里叶变换
• void cv::magnitude ( InputArray x, InputArray y, OutputArray magnitude )计算和的模，

例子：

// https://docs.opencv.org/4.x/d8/d01/tutorial_discrete_fourier_transform.html
#include "opencv2/core.hpp"
#include "opencv2/imgproc.hpp"
#include "opencv2/imgcodecs.hpp"
#include "opencv2/highgui.hpp"

#include <iostream>

using namespace cv;
using namespace std;

static void help(char ** argv)
{
    cout << endl
        <<  "This program demonstrated the use of the discrete Fourier transform (DFT). " << endl
        <<  "The dft of an image is taken and it's power spectrum is displayed."  << endl << endl
        <<  "Usage:"                                                                      << endl
        << argv[0] << " [image_name -- default lena.jpg]" << endl << endl;
}

int main(int argc, char ** argv)
{
    help(argv);

    const char* filename = argc >=2 ? argv[1] : "lena.jpg";

    Mat I = imread( samples::findFile( filename ), IMREAD_GRAYSCALE);
    if( I.empty()){
        cout << "Error opening image" << endl;
        return EXIT_FAILURE;
    }

    //! [expand]
    Mat padded;                            //expand input image to optimal size
    int m = getOptimalDFTSize( I.rows );
    int n = getOptimalDFTSize( I.cols ); // on the border add zero values
    copyMakeBorder(I, padded, 0, m - I.rows, 0, n - I.cols, BORDER_CONSTANT, Scalar::all(0));
    //! [expand]

    //! [complex_and_real]
    Mat planes[] = {Mat_<float>(padded), Mat::zeros(padded.size(), CV_32F)};
    Mat complexI;
    merge(planes, 2, complexI);         // Add to the expanded another plane with zeros
    //! [complex_and_real]

    //! [dft]
    dft(complexI, complexI);            // this way the result may fit in the source matrix
    //! [dft]

    // compute the magnitude and switch to logarithmic scale
    // => log(1 + sqrt(Re(DFT(I))^2 + Im(DFT(I))^2))
    //! [magnitude]
    split(complexI, planes);                   // planes[0] = Re(DFT(I), planes[1] = Im(DFT(I))
    magnitude(planes[0], planes[1], planes[0]);// planes[0] = magnitude
    Mat magI = planes[0];
    //! [magnitude]

    //! [log]
    magI += Scalar::all(1);                    // switch to logarithmic scale
    log(magI, magI);
    //! [log]

    //! [crop_rearrange]
    // crop the spectrum, if it has an odd number of rows or columns
    magI = magI(Rect(0, 0, magI.cols & -2, magI.rows & -2));

    // rearrange the quadrants of Fourier image  so that the origin is at the image center
    int cx = magI.cols/2;
    int cy = magI.rows/2;

    Mat q0(magI, Rect(0, 0, cx, cy));   // Top-Left - Create a ROI per quadrant
    Mat q1(magI, Rect(cx, 0, cx, cy));  // Top-Right
    Mat q2(magI, Rect(0, cy, cx, cy));  // Bottom-Left
    Mat q3(magI, Rect(cx, cy, cx, cy)); // Bottom-Right

    Mat tmp;                           // swap quadrants (Top-Left with Bottom-Right)
    q0.copyTo(tmp);
    q3.copyTo(q0);
    tmp.copyTo(q3);

    q1.copyTo(tmp);                    // swap quadrant (Top-Right with Bottom-Left)
    q2.copyTo(q1);
    tmp.copyTo(q2);
    //! [crop_rearrange]

    //! [normalize]
    normalize(magI, magI, 0, 1, NORM_MINMAX); // Transform the matrix with float values into a
                                            // viewable image form (float between values 0 and 1).
    //! [normalize]
    imshow("Input Image"       , I   );    // Show the result
    imshow("spectrum magnitude", magI);
    waitKey();

    return EXIT_SUCCESS;
}

结果：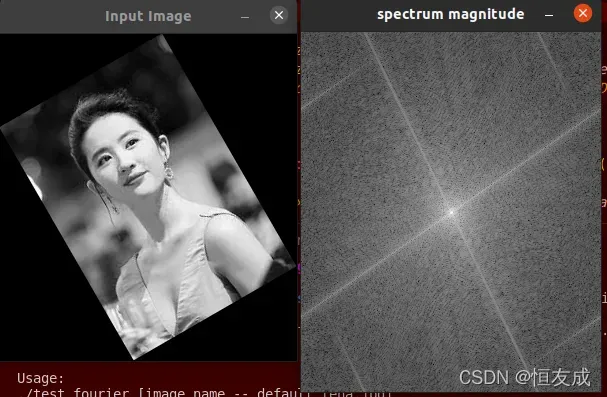

REF:

1.https://zhuanlan.zhihu.com/p/351173878
2.https://zhuanlan.zhihu.com/p/19763358
3.https://zhuanlan.zhihu.com/p/31371519
4.https://docs.opencv.org/4.x/d8/d01/tutorial_discrete_fourier_transform.html
5.https://www.cnblogs.com/HL-space/p/10546602.html