一、理论基础
1、混沌博弈优化算法
混沌博弈优化(Chaos game optimization, CGO)算法是基于混沌理论的原理提出的一种优化算法,它利用分形和混沌博弈的基本概念,建立了CGO算法的数学模型。
在该算法中,每个候选解()由一些决策变量(
)组成,这些决策变量代表这些合格种子在Sierpinski三角形中的位置。在该算法中,Sierpinski三角形被视为候选解的搜索空间。数学模型如下:
其中,
是Sierpinski三角形(搜索空间)内合格种子(候选解)的数量,
是这些种子的维数。
这些合格种子的初始位置在搜索空间中随机确定如下: 其中
代表合格种子的初始位置;
和
是
候选解的
决策变量的最小值和最大值;
是区间
中的随机数。
该数学模型的主要概念是在搜索空间内创建不同的合格种子,以完成Sierpinski三角形的整体形状。对于搜索空间()中的每个合格种子,将绘制一个包含3个种子的临时三角形,如下所示:
- 迄今为止全局最优解(Global Best,
)
- 种群的平均位置(Mean Group,
)
- 第i个候选解(
)作为所选种子的位置
其中,是目前找到的合格水平最高的最佳候选解,
是随机选取的一些合格种子的平均值。
为了实现该算法的优化目标,开发了4种创建种子的方法。其中,第一个种子位于,第二个种子位于
,第三个种子位于
,第四个种子的位置基于随机候选解产生。
第一种子产生的过程的数学表示如下:其中,
是第
个候选解;
是迄今为止发现的全局最优解;
是一些选定的合格种子的平均值;
是随机生成的阶乘,用于模拟种子的移动限制,而
和
分别表示1或2的随机整数,用于模拟掷骰子的可能性。
与第一种子的移动过程类似,第二种子可以向和
之间的连接线的一点移动,并且使用一些随机生成的因子来限制该移动。该过程的数学表示如下:
其中,
是随机生成的阶乘,用于模拟种子的移动限制,而
和
分别表示1或2的随机整数,用于模拟掷骰子的可能性。其他参数如第一个种子所述。
第三个种子是根据的位置随机生成的,其数学模型如下:
为实现搜索空间中合格种子位置更新的变异阶段,还采用另一个过程生成第四个种子。这个种子的位置更新是基于随机选择的决策变量的一些随机变化。第四个种子的数学建模如下:
其中
是
区间内的随机整数,
是
区间内均匀分布的随机数。
为了控制和调整CGO算法的探索和利用率,针对提出了四种不同的公式,用于控制种子的移动限制:
其中,
是
区间内的均匀分布随机数,而
和
是
区间内的随机整数。
2、CGO算法伪代码
CGO算法伪代码如图1所示。
2. 仿真实验及结果分析
将CGO与GWO、WOA、SOS和TLBO进行对比,以常用23个测试函数的F1、F2(单峰函数/30维)、F10、F11(多峰函数/30维)和CEC2017测试函数的F6和F7(30维)为例,种群规模设置为50,最大迭代次数设置为500,每个算法独立运算30次。结果显示如下: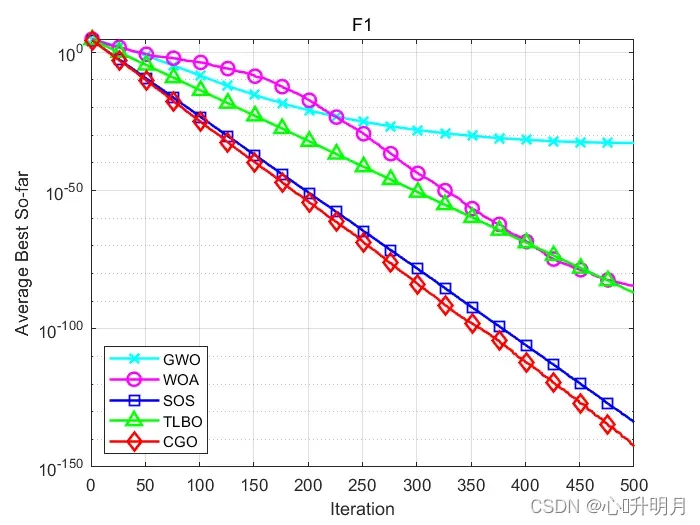
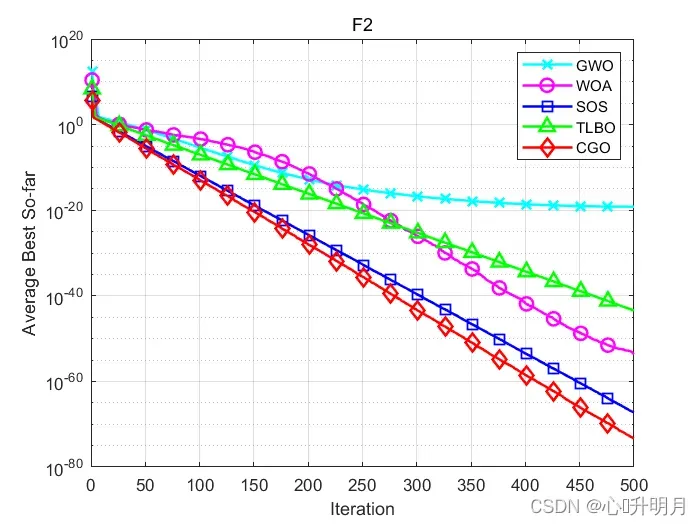
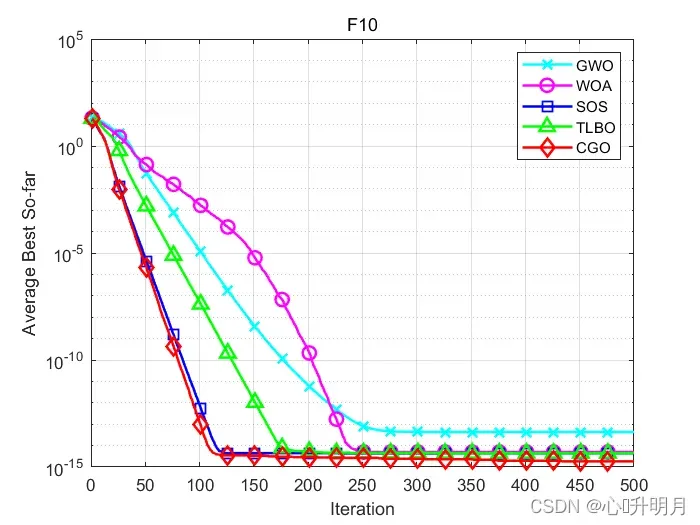
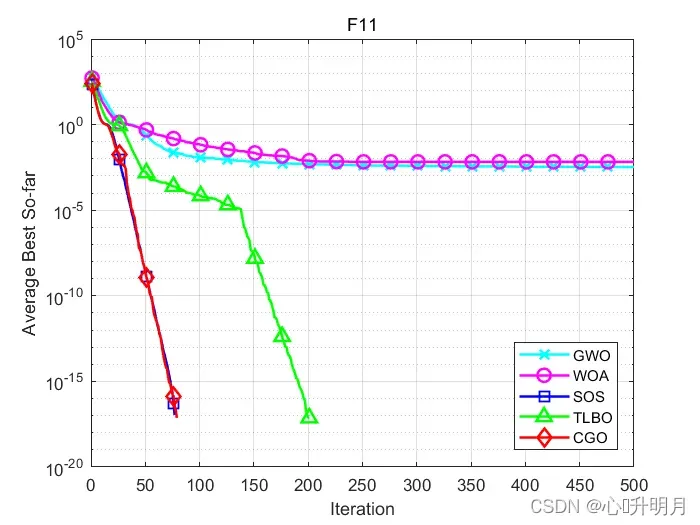
函数:F1
GWO:最差值: 9.0138e-33,最优值:5.5583e-35,平均值:1.6987e-33,标准差:1.8232e-33,秩和检验:3.0199e-11
WOA:最差值: 6.3404e-84,最优值:5.0426e-95,平均值:3.7613e-85,标准差:1.262e-84,秩和检验:3.0199e-11
SOS:最差值: 1.9813e-133,最优值:2.0348e-136,平均值:1.4282e-134,标准差:3.5494e-134,秩和检验:3.0199e-11
TLBO:最差值: 3.963e-87,最优值:1.6727e-89,平均值:1.0494e-87,标准差:1.1013e-87,秩和检验:3.0199e-11
CGO:最差值: 3.9198e-142,最优值:4.9139e-150,平均值:2.3955e-143,标准差:8.0333e-143,秩和检验:1
函数:F2
GWO:最差值: 1.859e-19,最优值:6.1822e-21,平均值:6.5773e-20,标准差:4.5807e-20,秩和检验:3.0199e-11
WOA:最差值: 5.5072e-53,最优值:1.7111e-59,平均值:2.2437e-54,标准差:1.0037e-53,秩和检验:3.0199e-11
SOS:最差值: 3.5483e-67,最优值:1.7269e-69,平均值:5.3583e-68,标准差:8.4905e-68,秩和检验:3.0199e-11
TLBO:最差值: 1.1781e-43,最优值:7.143e-45,平均值:3.5969e-44,标准差:2.394e-44,秩和检验:3.0199e-11
CGO:最差值: 5.6983e-73,最优值:0,平均值:4.4647e-74,标准差:1.1209e-73,秩和检验:1
函数:F10
GWO:最差值: 5.0626e-14,最优值:3.9968e-14,平均值:4.3165e-14,标准差:3.5343e-15,秩和检验:5.551e-12
WOA:最差值: 7.9936e-15,最优值:8.8818e-16,平均值:5.033e-15,标准差:2.8119e-15,秩和检验:1.2084e-05
SOS:最差值: 4.4409e-15,最优值:8.8818e-16,平均值:4.3225e-15,标准差:6.4863e-16,秩和检验:3.3774e-08
TLBO:最差值: 4.4409e-15,最优值:4.4409e-15,平均值:4.4409e-15,标准差:0,秩和检验:5.3591e-09
CGO:最差值: 4.4409e-15,最优值:8.8818e-16,平均值:1.8356e-15,标准差:1.5979e-15,秩和检验:1
函数:F11
GWO:最差值: 0.017041,最优值:0,平均值:0.0033471,标准差:0.0053964,秩和检验:0.0013702
WOA:最差值: 0.093766,最优值:0,平均值:0.0066683,标准差:0.021302,秩和检验:0.081523
SOS:最差值: 0,最优值:0,平均值:0,标准差:0,秩和检验:NaN
TLBO:最差值: 0,最优值:0,平均值:0,标准差:0,秩和检验:NaN
CGO:最差值: 0,最优值:0,平均值:0,标准差:0,秩和检验:NaN
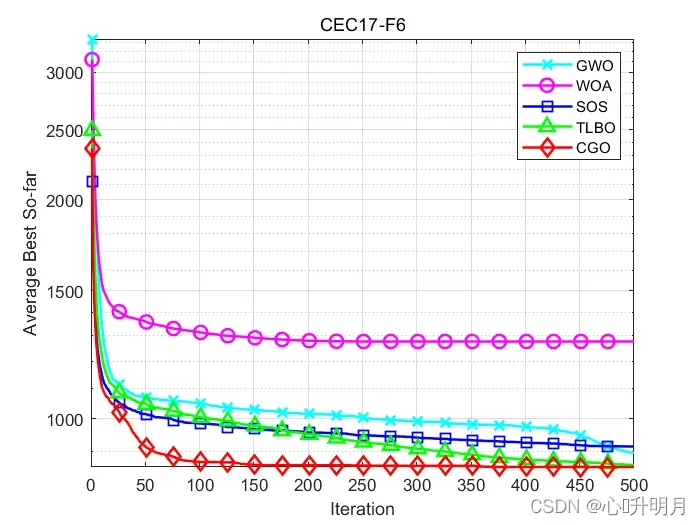
函数:CEC17-F6
GWO:最差值: 1008.7738,最优值:814.5043,平均值:897.0891,标准差:50.9036,秩和检验:0.0030339
WOA:最差值: 1448.0519,最优值:1119.6555,平均值:1276.6888,标准差:95.0696,秩和检验:3.0199e-11
SOS:最差值: 957.3604,最优值:851.0151,平均值:915.1328,标准差:27.5783,秩和检验:1.5964e-07
TLBO:最差值: 964.3504,最优值:803.85,平均值:862.9625,标准差:40.8144,秩和检验:0.48252
CGO:最差值: 975.0231,最优值:808.2228,平均值:857.5276,标准差:36.3624,秩和检验:1
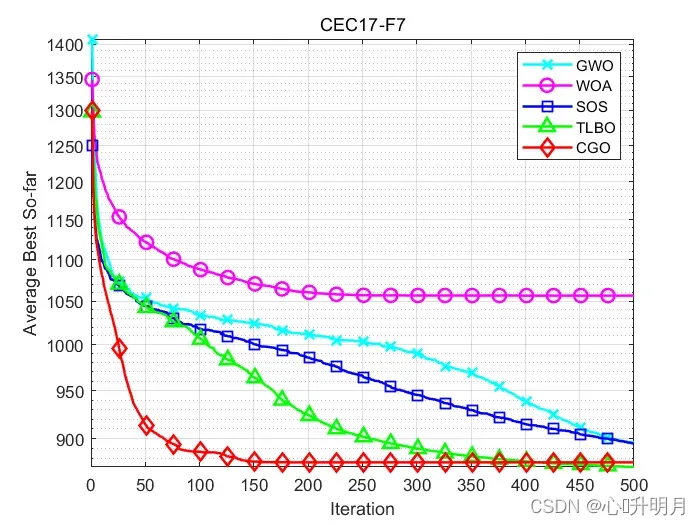
函数:CEC17-F7
GWO:最差值: 1041.3225,最优值:861.6842,平均值:896.2543,标准差:35.0411,秩和检验:0.014412
WOA:最差值: 1166.4361,最优值:976.7906,平均值:1056.624,标准差:54.2451,秩和检验:3.0199e-11
SOS:最差值: 956.527,最优值:843.8169,平均值:895.1846,标准差:36.0076,秩和检验:0.059428
TLBO:最差值: 906.1988,最优值:843.0764,平均值:872.0592,标准差:16.7959,秩和检验:0.40354
CGO:最差值: 922.3795,最优值:843.7781,平均值:876.6448,标准差:21.91,秩和检验:1
所得结果证明:在大多数情况下,CGO优于其他启发式算法。
3. 参考文献
[1] Talatahari, S., Azizi, M.Chaos Game Optimization: a novel metaheuristic algorithm[J]。Artificial Intelligence Review, 2021, 54: 917-1004.
版权声明:本文为博主心️升明月原创文章,版权归属原作者,如果侵权,请联系我们删除!
原文链接:https://blog.csdn.net/weixin_43821559/article/details/123209143
