前言
从机器学习到模式识别,已经遇到了很多次EM算法,但是好像并没有真正的理解,本篇文章将从浅到深,从通俗的语言到数学推导来讲解这个算法。
(这里默认大家都已经掌握了极大似然的思想)
简介
EM算法(Expectation-maximization algorithm),期望最大算法,是在概率模型中寻找参数最大似然估计或者最大后验估计的算法,其中概率模型依赖于无法观测的隐性变量。
EM算法经过两个步骤交替进行计算:
- 计算期望(E),利用对隐藏变量的现有估计值,计算其最大似然估计值;
- 最大化(M),最大化在E步上求得的最大似然值来计算参数的值。M步上找到的参数估计值被用于下一个E步计算中,这个过程不断交替进行。
示例1
假如有两枚硬币A和B,随机抛掷后正面朝上的概率为
P
A
,
P
B
P_A,P_B
PA,PB。假如我们已轮流抛掷硬币A,B,每一轮抛五次,进行5轮,所得结果如下:
| 硬币 | 结果 | 统计 |
|---|---|---|
| A | 正正反正反 | 3正-2反 |
| B | 反反正正反 | 2正-3反 |
| A | 正反反反反 | 1正-4反 |
| B | 正反反正正 | 3正-2反 |
| A | 反正正反反 | 2正-3反 |
在这个问题中,我们要做的是极大似然估计,即通过一观测到的这5行结果,来估计参数
P
A
,
P
B
P_A,P_B
PA,PB。
以最大似然的思想,
P
A
P_A
PA直接等与
正
的
次
数
总
次
数
\frac{正的次数}{总次数}
总次数正的次数时达到最大似然。
现在,引入隐变量,就是说我们并不知道每一轮抛的是硬币A or B,只知道结果,也就是如下表格:
| 硬币 | 结果 | 统计 |
|---|---|---|
| … | 正正反正反 | 3正-2反 |
| … | 反反正正反 | 2正-3反 |
| … | 正反反反反 | 1正-4反 |
| … | 正反反正正 | 3正-2反 |
| … | 反正正反反 | 2正-3反 |
即类似如下的隐马尔科夫模型:
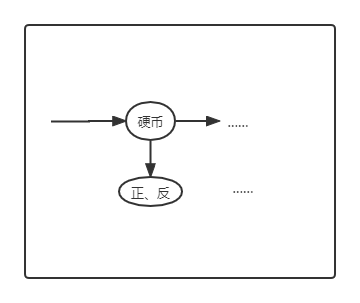
这种情况下,我们该如何去最大似然
P
A
,
P
B
P_A,P_B
PA,PB,如果还按照之前的思想,那需要知道每一轮抛的是哪个硬币,但是想要知道每一轮抛的那个硬币,就需要知道
P
A
,
P
B
P_A,P_B
PA,PB才能去做似然估计,看起来是一个死锁无法解决的问题,接下来就正式引入EM算法,一起来领略下它的美丽:
EM算法的思想就是,先随机初始化
P
A
,
P
B
P_A,P_B
PA,PB,用初始化的
P
A
,
P
B
P_A,P_B
PA,PB去估计每一轮抛的哪一个硬币,然后再根据所得结果更新
P
A
,
P
B
P_A,P_B
PA,PB,重复此过程直至收敛。
即:
- 随机初始
P
A
=
0.2
,
P
B
=
0.7
P_A=0.2,P_B=0.7
PA=0.2,PB=0.7; - 求解每一轮抛哪个硬币使得到对应结果的概率最大:
| 轮数 | 若为硬币A | 若为硬币B |
|---|---|---|
| 1 | 0.00512,即0.2 0.2 0.2 0.8 0.8,3正-2反 | 0.03087,3正-2反 |
| 2 | 0.02048,即0.2 0.2 0.8 0.8 0.8,2正-3反 | 0.01323,2正-3反 |
| 3 | 0.08192,即0.2 0.8 0.8 0.8 0.8,1正-4反 | 0.00567,1正-4反 |
| 4 | 0.00512,即0.2 0.2 0.2 0.8 0.8,3正-2反 | 0.03087,3正-2反 |
| 5 | 0.02048,即0.2 0.2 0.8 0.8 0.8,2正-3反 | 0.01323,2正-3反 |
如上表格,根据极大似然的思想选择对概率大的,则:
第1轮中最有可能的是硬币B
第2轮中最有可能的是硬币A
第3轮中最有可能的是硬币A
第4轮中最有可能的是硬币B
第5轮中最有可能的是硬币A;
- 更新
P
A
,
P
B
P_A,P_B
PA,PB分别为
5
15
,
6
10
\frac{5}{15},\frac{6}{10}
155,106; - 重复上述三个步骤直至收敛。
示例2
接下来举一个更复杂的例子,即EM求解隐马尔科夫模型的参数(HMM三大问题中的模型参数的学习问题)。
记一个隐马尔科夫模型为
(
A
,
B
,
π
)
(A,B,\pi)
(A,B,π),其中A为状态转移矩阵,B为观测(发射)概率矩阵,
π
\pi
π为初始状态概率向量,I为状态序列,O为观测序列(一个观测序列可能有多种对应的状态序列)图示如下:
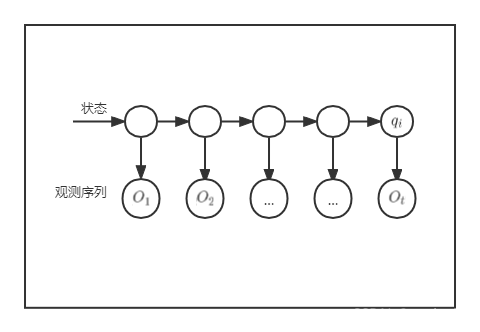
我们需要做的是,已知观测序列,估计参数
λ
=
(
A
,
B
,
π
)
\lambda=(A,B,\pi)
λ=(A,B,π),基于EM算法的Baum-Welch求解思想如下:
我们要最大化的目标是:
P
(
O
∣
λ
)
=
∑
I
P
(
O
,
I
∣
λ
)
=
∑
I
P
(
O
∣
λ
,
I
)
P
(
I
∣
λ
)
P(O|\lambda)=\sum_{I}P(O,I|\lambda) =\sum_{I}P(O|\lambda,I)P(I|\lambda)
P(O∣λ)=I∑P(O,I∣λ)=I∑P(O∣λ,I)P(I∣λ)
算法中的Q函数定义如下:
Q
(
λ
,
λ
(
i
)
)
=
E
z
[
l
o
g
P
(
I
,
O
∣
λ
)
∣
O
,
λ
(
i
)
]
Q(\lambda,\lambda^{(i)})=E_z[logP(I,O|\lambda)|O,\lambda^{(i)}]
Q(λ,λ(i))=Ez[logP(I,O∣λ)∣O,λ(i)]
即:
Q
(
λ
,
λ
(
i
)
)
=
∑
I
l
o
g
P
(
I
,
O
∣
λ
)
P
(
O
,
I
∣
λ
(
i
)
)
Q(\lambda,\lambda^{(i)})=\sum_{I}logP(I,O|\lambda)P(O,I|\lambda^{(i)})
Q(λ,λ(i))=I∑logP(I,O∣λ)P(O,I∣λ(i))
其中迭代求解的过程就是在不断的最大化Q函数。
1.初始化
λ
\lambda_0
λ0,计算所有I情况下的
P
(
O
,
I
∣
λ
(
i
)
)
P(O,I|\lambda^{(i)})
P(O,I∣λ(i))并带入Q函数,(需要明确的就是当
λ
\lambda_0
λ0和观测序列已经知道的时候。所有可能的状态序列的概率是可以算出来的,这里不再过多解释)
2.Q函数可分解为三项,分别对每一项用拉格朗日求解极大值点,得到参数更新公式。
(这里先大概了解下大概思想就好,具体的推导见Baum-Welch的推导)
EM算法
接下来我们正式的进入一般形式的EM算法。
推导流程可见这篇博客,非常清晰
EM算法
正文
本篇文章将从另一个角度说明EM算法的E和M步骤都增大了对数似然函数的一个良好定义的下界的值,并且完整的EM循环会使得模型的参数向着使对数似然函数增大的方向进行改变(除非已经收敛),如下:
记观测变量为X,隐变量为Z,参数
θ
\theta
θ,我们最大化的目标函数是(通俗的解释就是说观测变量可能有多种对应的状态序列,那我们求和即可):
P
(
X
∣
θ
)
=
∑
Z
P
(
X
,
Z
∣
θ
)
P(X|\theta)=\sum_{Z}P(X,Z|\theta)
P(X∣θ)=Z∑P(X,Z∣θ)
引入一个定义在隐变量上的分布
q
(
Z
)
q(Z)
q(Z)
易推导下式成立:
l
n
P
(
X
∣
θ
)
=
L
(
q
,
θ
)
+
K
L
(
q
∣
∣
p
)
lnP(X|\theta)=L(q,\theta)+KL(q||p)
lnP(X∣θ)=L(q,θ)+KL(q∣∣p)
其中:
L
(
q
,
θ
)
=
∑
Z
q
(
Z
)
l
n
{
p
(
X
,
Z
∣
θ
)
q
(
Z
)
}
L(q,\theta)=\sum_Zq(Z)ln\{\frac{p(X,Z|\theta)}{q(Z)}\}
L(q,θ)=Z∑q(Z)ln{q(Z)p(X,Z∣θ)}
K
L
(
q
∣
∣
p
)
=
−
∑
Z
q
(
Z
)
l
n
{
p
(
Z
∣
X
,
θ
)
q
(
Z
)
}
KL(q||p)=-\sum_Zq(Z)ln\{\frac{p(Z|X,\theta)}{q(Z)}\}
KL(q∣∣p)=−Z∑q(Z)ln{q(Z)p(Z∣X,θ)}
(把这两个式子拆开待会原式就可以证出来)
我们可以发现,
K
L
(
q
∣
∣
p
)
KL(q||p)
KL(q∣∣p)表示的其实是
q
(
Z
)
q(Z)
q(Z)和后验分布
p
(
Z
∣
X
,
θ
)
p(Z|X,\theta)
p(Z∣X,θ)之间的KL散度,KL散度恒大于等于零,当且仅当两个概率分布相等时取零(由吉布斯等式可证),也就是说KL
≥
\geq0
≥0,
即,
l
n
P
(
X
∣
θ
)
≥
L
(
q
,
θ
)
lnP(X|\theta)\geq L(q,\theta)
lnP(X∣θ)≥L(q,θ)
表示
L
(
q
,
θ
)
L(q,\theta)
L(q,θ)是
l
n
P
(
X
∣
θ
)
lnP(X|\theta)
lnP(X∣θ)的一个下界。
而EM就是在不断优化这个下界,从而达到最大化目标函数的效果。
(这个下届是个凹函数)
E步
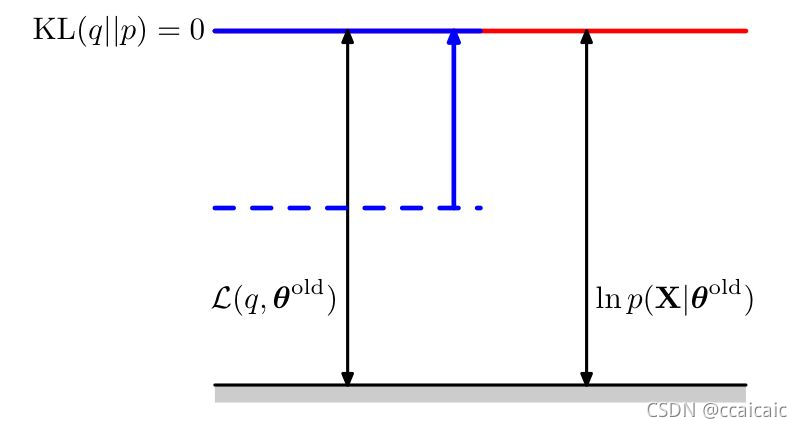
在E步中,q分布被更新为当前参数值下的后验概率分布,即KL式等于0,这使得下界上移到与对数函似然函数值相同的位置。
M步
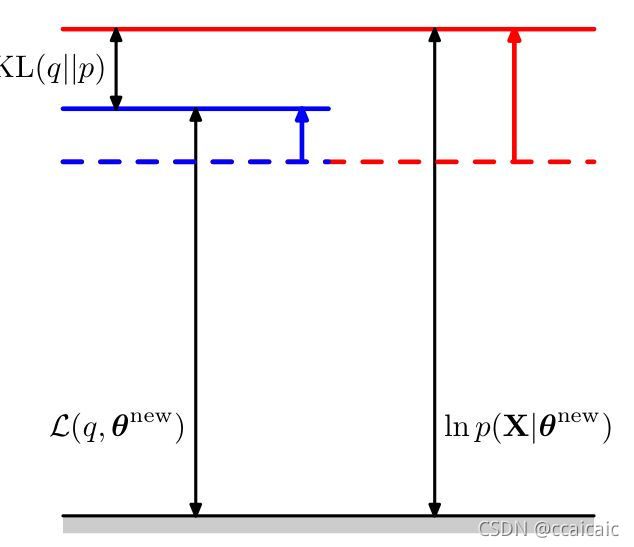
在M步,固定E步得到的
q
(
Z
)
q(Z)
q(Z),下界关于参数最大化从而更新
θ
\theta
θ。由于KL散度非负,故对数似然函数的增量至少与下界的增量相等。
综上,个人理解:观测序列已知,E步其实就是初始化参数,然后根据参数和观测序列得到隐变量的分布或者说所有可能的状态序列;M步就是根据E步得到的状态序列以及已有的观测序列去更新参数,从而反复迭代,直至不变收敛。
版权声明:本文为博主ccaicaic原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接和本声明。
原文链接:https://blog.csdn.net/m0_49673695/article/details/121424438
