线性代数初等变换

初等变换–分初等行(列)变换

定理:任意矩阵都可以通过初等变换化为,标准形矩阵.

标准形1,第一个必须是开头是1,左上角开始一串1(不能断),不一定是方阵

$\left( \begin {aligned} 1 & \ & 0 & \ & \ 0 & & \ 0\\0 & \ & 1 & \ & \ { 0} & & 0\\ 0 & \ & 0 & \ & \ 1 & & 0 \\ 0 & \ & 0 & \ & \ 0 & & 1\end{aligned} \right )$ 像这样可以. $\left( \begin {aligned} 1 & \ & 0 & \ & \ 0 \\0 & \ & 1 & \ & \ { 0} \\ 0 & \ & 0 & \ & \0 \end{aligned} \right )$ ,也可以这样 $\left( \begin {aligned} 1 & \ & 0 & \ & \ 0 \\0 & \ & 0 & \ & \ { 0} \\ 0 & \ & 0 & \ & \ 0 \end{aligned} \right )$ , $\left( \begin {aligned} 0 & \ & 0 & \ & \ 0 \\0 & \ &0 & \ & \ { 0} \\ 0 & \ & 0 & \ & \ 0 \end{aligned} \right )$ 最后一个就是行列式是0 了.

初等变换包括以下几种:

1交换两行,行列式的值变号

$\left( \begin {aligned} 1 & \ & 0 & \ & \ 0 & & \ 0\\0 & \ & 1 & \ & \ { 0} & & 0\\ 0 & \ & 0 & \ & \ 1 & & 0 \\ 0 & \ & 0 & \ & \ 0 & & 1 \end{aligned} \right )$ 交换1,3两行—> $\left( \begin {aligned} 0 & \ & 0 & \ & \ 1 & & \ 0\\0 & \ & 1 & \ & \ { 0} & & 0\\ 1 & \ & 0 & \ & \ 0 & & 0 \\ 0 & \ & 0 & \ & \ 0 & & 1 \end{aligned} \right )$ 行列式记作 $\left | E(i, j ) \right | =-1$

2, 用非零k乘以某行, $\left( \begin {aligned} 1 & \ & 0 & \ & \ 0 & & \ 0\\0 & \ & 1 & \ & \ { 0} & & 0\\ 0 & \ & 0 & \ & \ 1 & & 0 \\ 0 & \ & 0 & \ & \ 0 & & 1 \end{aligned} \right )$ —>第三行乘5 $\left( \begin {aligned} 1 & \ & 0 & \ & \ 0 & & \ 0\\0 & \ & 1 & \ & \ { 0} & & 0\\ 0 & \ & 0 & \ & \ 5 & & 0 \\ 0 & \ & 0 & \ & \ 0 & & 1 \end{aligned} \right )$

3,某行乘以l倍加到另外一行 $\left( \begin {aligned} 1 & \ & 0 & \ & \ 0 & & \ 0\\0 & \ & 1 & \ & \ { 0} & & 0\\ 0 & \ & 0 & \ & \ 1 & & 0 \\ 0 & \ & 0 & \ & \ 0 & & 1 \end{aligned} \right )$ —->第三行乘5 加到第一行 $\left( \begin {aligned} 1 & \ & 0 & \ & \ 5 & & \ 0\\0 & \ & 1 & \ & \ { 0} & & 0\\ 0 & \ & 0 & \ & \ 1 & & 0 \\ 0 & \ & 0 & \ & \ 0 & & 1 \end{aligned} \right )$

行列式记作: $\left | E(i, j(k)) \right | = 1$

初等方阵是对单位阵进行一次初等变换(行,列)

1,初等方阵均可逆,

2,初等方阵的转置也是初等方阵,

3,逆矩阵的也是初等方阵

E(2(3)) = $\left( \begin {aligned} 1 & \ & 0 & \ & \ {0} \\ 0 & \ & 3 & \ & \ { 0} \\ 0 & \ & 0 & \ & \ 1 \end{aligned} \right )$ ,第二行乘以3,

E(1,3) = $\left( \begin {aligned} 0 & \ & 0 & \ & \ {1} \\ 0 & \ & 1 & \ & \ {0} \\ 1 & \ & 0 & \ & \ 0 \end{aligned} \right )$ 交换1,3行

例如A = $\left( \begin {aligned} 1 & \ & 2 & \ & \ {3} \\ 4 & \ & 5 & \ & \ {6} \\ 7 & \ & 8 & \ & \ 9 \end{aligned} \right )$ ,

E(2(3)) A = $\left( \begin {aligned} 1 & \ & 0 & \ & \ {0} \\ 0 & \ & 3 & \ & \ { 0} \\ 0 & \ & 0 & \ & \ 1 \end{aligned} \right )$ $\left( \begin {aligned} 1 & \ & 2 & \ & \ {3} \\ 4 & \ & 5 & \ & \ {6} \\ 7 & \ & 8 & \ & \ 9 \end{aligned} \right )$ = $\left( \begin {aligned} 1 & \ & 2 & \ & \ {3} \\ 12 & \ & 15 & \ & \ 18 \\ 7 & \ & 8 & \ & \ 9 \end{aligned} \right )$ ,左乘A ,用3乘A的第二行

AE(1,3) = $\left( \begin {aligned} 1 & \ & 2 & \ & \ {3} \\ 4 & \ & 5 & \ & \ {6} \\ 7 & \ & 8 & \ & \ 9 \end{aligned} \right )$ $\left( \begin {aligned} 0 & \ & 0 & \ & \ {1} \\ 0 & \ & 1 & \ & \ {0} \\ 1 & \ & 0 & \ & \ 0 \end{aligned} \right )$ = $\left( \begin {aligned} 3 & \ & 2 & \ & \ {1} \\6 & \ & 5 & \ & \ { 4} \\ 9 & \ & 8 & \ & \ 7 \end{aligned} \right )$ ,有乘A, 交换A的1,3

左乘行,右乘列

AE(1(4)) = $\left( \begin {aligned} 1 & \ & 2 & \ & \ {3} \\ 4 & \ & 5 & \ & \ {6} \\ 7 & \ & 8 & \ & \ 9 \end{aligned} \right )$ $\left( \begin {aligned} 4 & \ & 0 & \ & \ {0} \\ 0 & \ & 1 & \ & \ {0} \\ 0 & \ & 0 & \ & \ 1 \end{aligned} \right )$ = $\left( \begin {aligned} 4 & \ & 2 & \ & \ 3 \\ 8 & \ & 5 & \ & \ {6} \\ 28 & \ & 8 & \ & \ 9 \end{aligned} \right )$

定理:任意矩阵经过初等变换,P1,P2,…Ps , Q1,Q2,…,Qt

$P_s...P_2P_1AQ_1Q_2...Q_t$ 化为标注形

推论:A,B等价 == 存在可逆矩阵P,Q, PAQ = B

A经过初等变换为B

$P_s...P_2P_1AQ_1Q_2...Q_t$ = B

定理2:A可逆,A的标准形为E

必要条件:A可逆,标注形为D

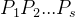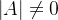
定理3:A可逆,A= $P_1P_2...P_s$ , $\left | A \right | \neq 0$

A = $P_1^{-1}P_2^{-1}...P_s^{-1}E Q_t^{-1}...Q_2^{-1}Q_1^{-1}$

初等变换法:

(A,E)—>(E, $A^{-1}$ )

A = $\left( \begin {aligned} 1 & \ & 1 & \ & \ {1} \\ 2 & \ & 1 & \ & \ { 0} \\ -3 & \ &2 & \ & \ -5 \end{aligned} \right )$ ,求 $A^{-1}$

(A, E) = $\left( \begin {aligned} 1 & \ & 1 & \ & \ {1} \\ 2 & \ & 1 & \ & \ { 0} \\ -3 & \ &2 & \ & \ -5 \end{aligned} \right )$ $\left( \begin {aligned} 1 & \ & 0 & \ & \ {0} \\0 & \ & 1 & \ & \ { 0} \\ 0 & \ &0 & \ & \ 1 \end{aligned} \right )$ 先对A削掉第一列的2,3行为0 第一行*(-2)加到第二行,第一行*3加到第三行

$\left( \begin {aligned} 1 & \ & 0 & \ & \ {1} & \ & \ {1}& \ & \ {0}& \ & \ {0}\\ 0 & \ & 1 & \ & \ { -2} & \ & \ {-2}& \ & \ {1}& \ & \ {0}\\ 0 & \ & 2& \ & \ -2 & \ & \ {3}& \ & \ {0}& \ & \ {1}\end{aligned} \right )$ ,去掉第三行第二列2,第二行*(-2)加第三行

$\left( \begin {aligned} 1 & \ & 0 & \ & \ {1} & \ & \ {1}& \ & \ {0}& \ & \ {0}\\ 0 & \ & 1 & \ & \ { -2} & \ & \ {-2}& \ & \ {1}& \ & \ {0}\\ 0 & \ & 0& \ & \ 2 & \ & \ {7}& \ & \ {-2}& \ & \ {1}\end{aligned} \right )$ ,去掉第二行第三列-2,第三行*(1)加第二行,去掉第一行第3列1,第三行成(-1/2)加第一行,

$\left( \begin {aligned} 1 & \ & 0 & \ & \ {0} & \ & \ {-5/2}& \ & \ {1}& \ & \ {-1/2}\\ 0 & \ & 1 & \ & \ { 0} & \ & \ {5}& \ & \ {-1}& \ & \ {-1}\\ 0 & \ & 0& \ & \ 1 & \ & \ {7/2}& \ & \ {-1}& \ & \ {1/2}\end{aligned} \right )$ 最后去第三行,第三列2变1,第三行乘1/2

$A ^{-1}= \left( \begin {aligned} {-5/2} & \ & 1 & \ & \ {-1/2} \\ 5 & \ & -1 & \ & \ { 1} \\ {7/2} & \ & -1 & \ & \ {1/2} \end{aligned} \right )$

注意事项:

1,先第一列,再第二列,再第三列

2,写整行,对整行进行操作,

3,第一行处理, 就不处理

4,()—>()–>() 矩阵操作用箭头

5,只做行变换

6,不管是否可逆

等出结果需要验证 $AA^{-1} = E$

原文链接：https://blog.csdn.net/aa644128600/article/details/130093340