深入理解机器学习——概率图模型（Probabilistic Graphical Model）：马尔可夫随机场（Markov Random Field，MRF）

分类目录：《深入理解机器学习》总目录

马尔可夫随机场（Markov Random Field，MRF）是典型的马尔可夫网，这是一种著名的无向图模型，图中每个结点表示一个或一组变量，结点之间的边表示两个变量之间的依赖关系。马尔可夫随机场有一组势函数（Potential Functions），亦称“因子”（Factor），这是定义在变量子集上的非负实函数，主要用于定义概率分布函数。

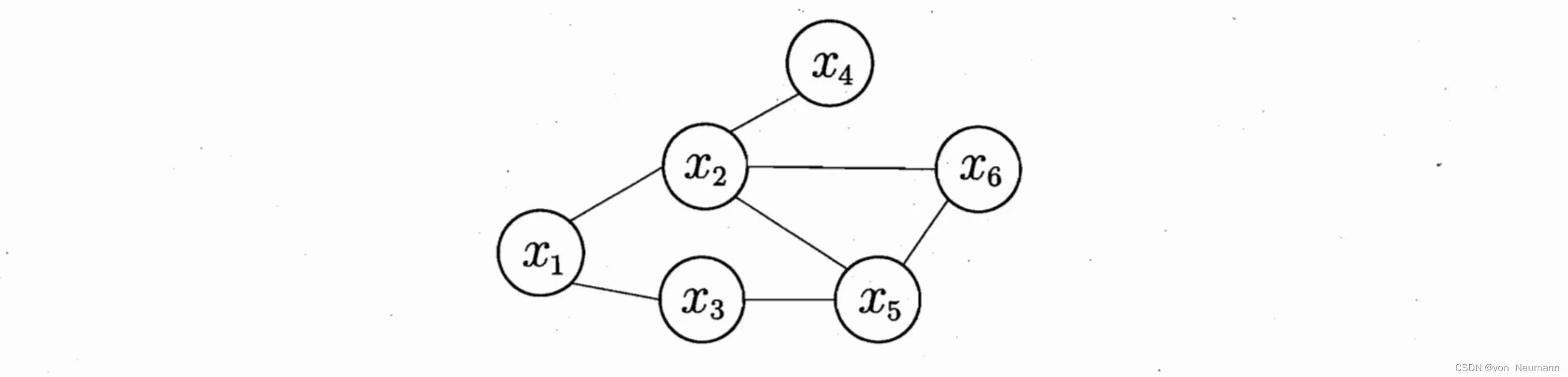
上图显示出一个简单的马尔可夫随机场，对于图中结点的一个子集，若其中任意两结点间都有边连接，则称该结点子集为一个“团”（Clique），若在一个团中加入另外任何一个结点都不再形成团，则称该团为“极大团（Maximal Clique）；换言之，极大团就是不能被其他团所包含的团，例如，在上图中、、、、、、和都是团，并且除了、和之外都是极大团；但是，因为和之间缺乏连接，并不构成团，显然，每个结点至少出现在一个极大团中。

在马尔可夫随机场中，多个变量之间的联合概率分布能基于团分解为多个因子的乘积，每个因子仅与一个团相关，具体来说，对于个变量，所有团构成的集合为，与团对应的变量集合记为，则联合概率定义为：

其中为与团对应的势函数，用于对团中的变量关系进行建模，为规范化因子，以确保是被正确定义的概率，在实际应用中，精确计算通常很困难，但许多任务往往并不需获得的精确值显然，若变量个数较多，则团的数目将会很多（例如，所有相互连接的两个变量都会构成团），这就意味着上式会有很多乘积项，显然会给计算带来负担。注意到若团不是极大团，则它必被一个极大团所包含，即。这意味着变量之间的关系不仅体现在势函数中，还体现在中。于是，联合概率可基于极大团来定义。假定所有极大团构成的集合为，则有：

如上图中，联合概率分布定义为：

其中，势函数定义在极大团上，由于它的存在，使我们不再需为团、和构建势函数。

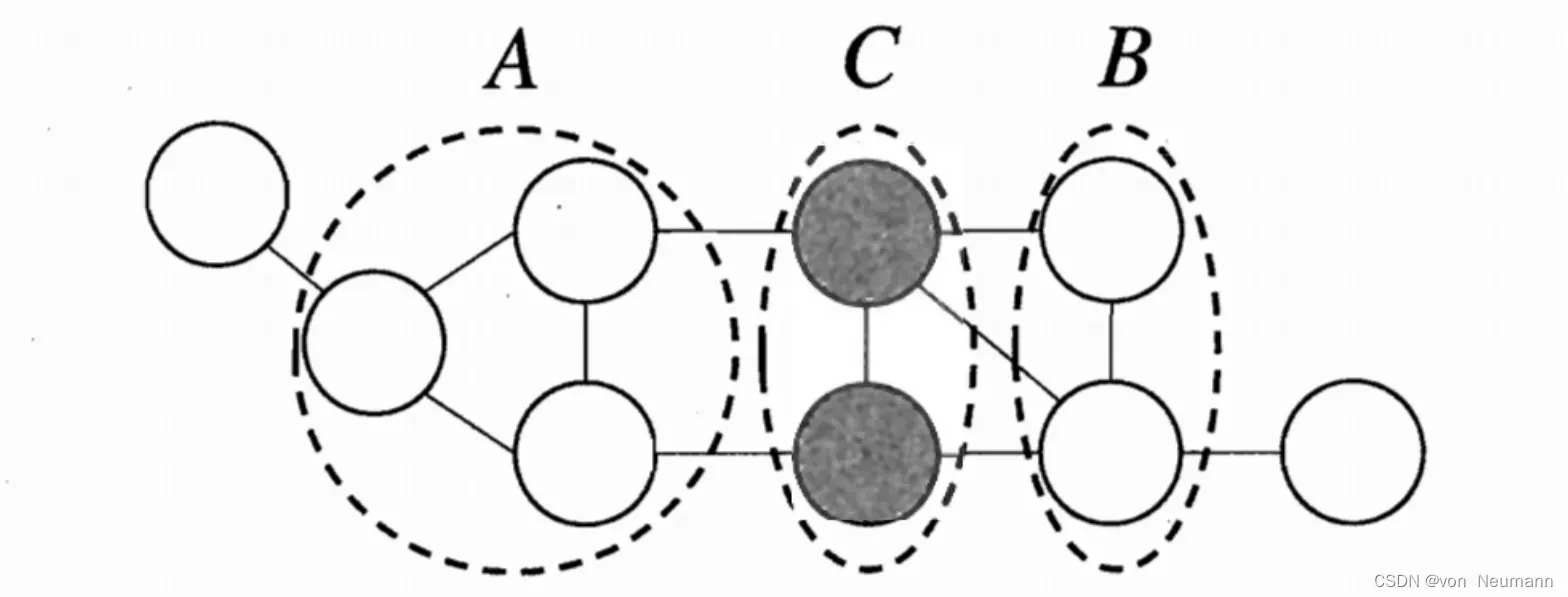
在马尔可夫随机场中如何得到“条件独立性”呢？同样借助“分离”的概念，如下图所示，若从结点集中的结点到中的结点都必须经过结点集 中的结点，则称结点集和被结点集分离，称为“分离集（Separating Set）。对马尔可夫随机场，有全局马尔可夫性（Global Markov Property），即给定两个变量子集的分离集，则这两个变量子集条件独立。如下图，若令、和对应的变量集分别为，和，则和在给定的条件下独立，记为：。

• 局部马尔可夫性（Local Markov Property）：给定某变量的邻接变量，则该变量条件独立于其他变量。形式化地说，令为图的结点集，为结点在图上的邻接结点，，则有
• 成对马尔可夫性（Pairwise Markov Property）：给定所有其他变量，两个非邻接变量条件独立。形式化地说，令图的结点集和边集分别为和，对图中的两个结点和，若，则

现在我们来考察马尔可夫随机场中的势函数，显然，势函数的作用是定量刻画变量集中变量之间的相关关系，它应该是非负函数，且在所偏好的变量取值上有较大函数值，例如，假定上图的变量均为二值变量，若势函数为：

则说明该模型偏好变量与拥有相同的取值，与拥有不同的取值；换言之，在该模型中与正相关，与负相关。所以，令与相同且与不同的变量值指派将取得较高的联合概率，为了满足非负性，指数函数常被用于定义势函数，即：

其中，是一个定义在变量上的实值函数，常见形式为：

其中和是参数。上式中的第二项仅考虑单结点，第一项则考虑每一对结点的关系。

参考文献：
[1] 周志华. 机器学习[M]. 清华大学出版社, 2016.