神经网络特性介绍
三层BP神经网络可以逼近任意连续的函数。三层BP神经网络简单易行,可靠性好,故只选择一个隐含层。
假设隐藏层单元数为,输入层单元数为
,输出层单元数为
,有一个经验公式:
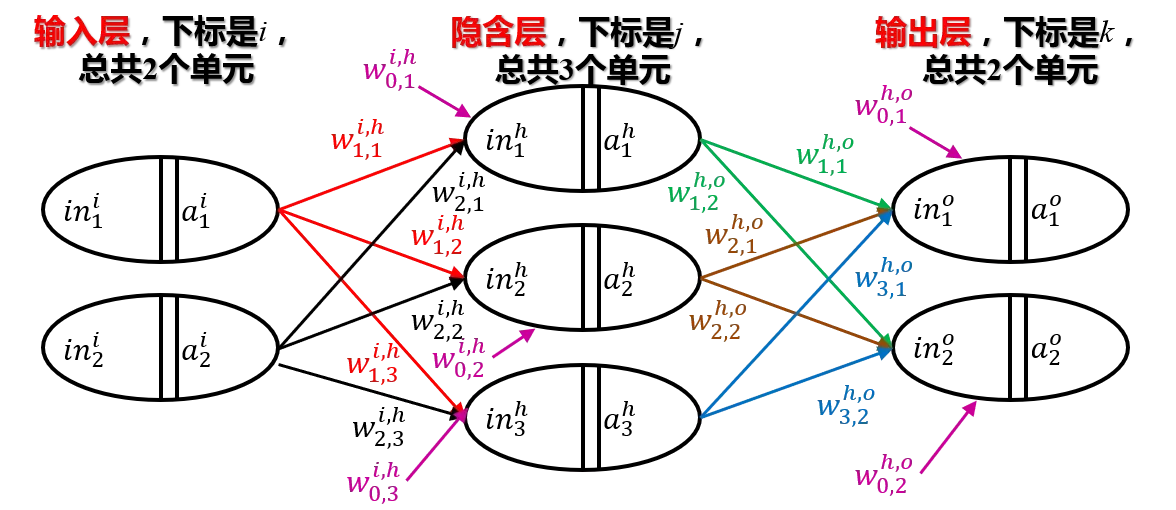
设层的输入为向量
,
单元的值为
第层的输出为向量
,第
单元的值为
从层的
th输出单元到
th层的
th输入单元的传递常数为
,形成矩阵
,其中
从
开始,具有常数项输入。
请注意,矩阵是根据索引的转置排列的。
信息前向传输
转移过程可以写成如下矩阵表达式:
展开式写成:
其中
每一层的输入和输出之间存在传递关系:
核函数
该函数为LOGISTIC函数,其具有微分性质:
有
这使得每一层的输出为的概率数。
设输入向量为,输出向量为
。输出向量与最后一层的输出顺序相同
有:
我们的目标是通过神经网络的输出来逼近输出
错误反向更新(第 2 层 → 第 3 层)
定义损失函数
设迭代次数为,梯度下降法公式
首先将从
层更新到
层:
所以:
记住:
所以:
写成矩阵形式,我们有
错误反向更新(第 1 层 → 第 2 层)
所以
认为
所以:
伪代码实现
从文件中获取
从文件中获取定义函数FUN1(训练集输入x,训练集输出y)
中间隐藏层数
第一层输入
第一层的输出
第二层输入
第二层输出
第三层输入
第三层输出
第 1 层到第 2 层传输矩阵
第 2 层到第 3 层传输矩阵
增强向量
增强向量定义函数
定义错误
定义学习参数
定义迭代次数
损失函数的初始值被赋值
从第一层到第二层的传递矩阵的初始值赋值为
第二层到第三层的传递矩阵赋初值(第一次更新)
损失函数被赋予一个初始值
(死循环)
(错误反向更新)
(前传)if
,跳出循环
else
返回
、
定义函数FUN2(测试集
,
,
)
(总式:)
返回
文章出处登录后可见!
已经登录?立即刷新
