- 文献阅读:DeepNet: Scaling Transformers to 1,000 Layers
- 1. 文章简介
- 2. 核心技术点
- 1. DeepNet整体结构
- 2. 参数初始化考察
- 3. DeepNorm考察
- 3. 实验考察
- 1. 可行性考察
- 2. 有效性考察
- 4. 结论 & 思考
- 文献链接: https://arxiv.org/abs/2203.00555
1. 文章简介
这篇文章是我司前阵子发布的一篇对于transformer的优化文章,一作还是我室友兼师弟,也是挺有意思的。
这篇文章针对了当前经典的transformer模型在深度很深的情况下训练往往不稳定,容易发散的现象进行了一定的研究,对这个现象的原因进行了比较深入的分析,并基于此提出了一种deepnorm的layernorm方法,从而在数学上可以确保训练的稳定性。
基于此,文中直接把transformer的最大训练层数推到了1000层,视觉效果上是真的厉害。
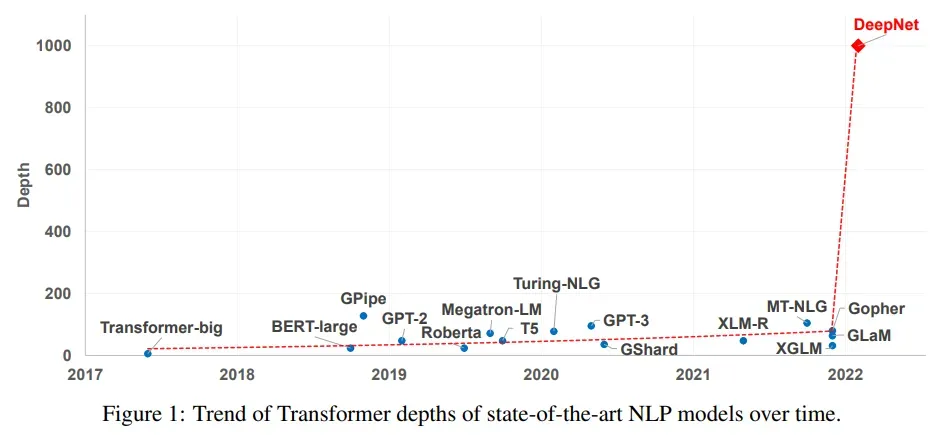
2. 核心技术点
1. DeepNet整体结构
文中主要的模型架构,即DeepNet的模型结构倒是相对简单,和传统的transformer其实只有一点微小的变动,具体包含以下两点:
- 调整参数初始化
- 调整残差设计
具体功能伪代码和超参数建议在文中直接给出如下:

下面,我们详细检查其具体假设和有效性分析。
2. 参数初始化考察
关于参数初始化为什么可以优化transformer训练稳定性的问题,我本人是了解的不太多,不过看文中的内容似乎已经有了几个对应的研究工作,比如以下三个:
- Improving Deep Transformer with Depth-Scaled Initialization and Merged Attention
- Improving Transformer Optimization Through Better Initialization
- Optimizing Deeper Transformers on Small Datasets
而在这篇文章当中,作者同样给出了一个可行的参数初始化优化方案,具体而言就是在ffn和value的参数初始化上调整正态分布的参数的标准差
,将其调整为gain为超参数
的Glorot初始化。
而关于Glorot初始化的定义,可以直接从torch的官网获取其定义。
综上,我们可以得到最终的参数初始化分布为:
其中,为参数矩阵的长宽,具体公式为:
特别的,对于self-attention,其初始化参数参数分布就是,其中
就是模型的维度。
关于超参数的选择,论文中给出的定义是:
其中,表示transformer的总的层数,而
表示对应的transformer的层数。
显然,越是下层,越小,参数初始化约接近于0。
关于不同初始化下模型梯度随层数的变化,论文中给出的实验结果如下:
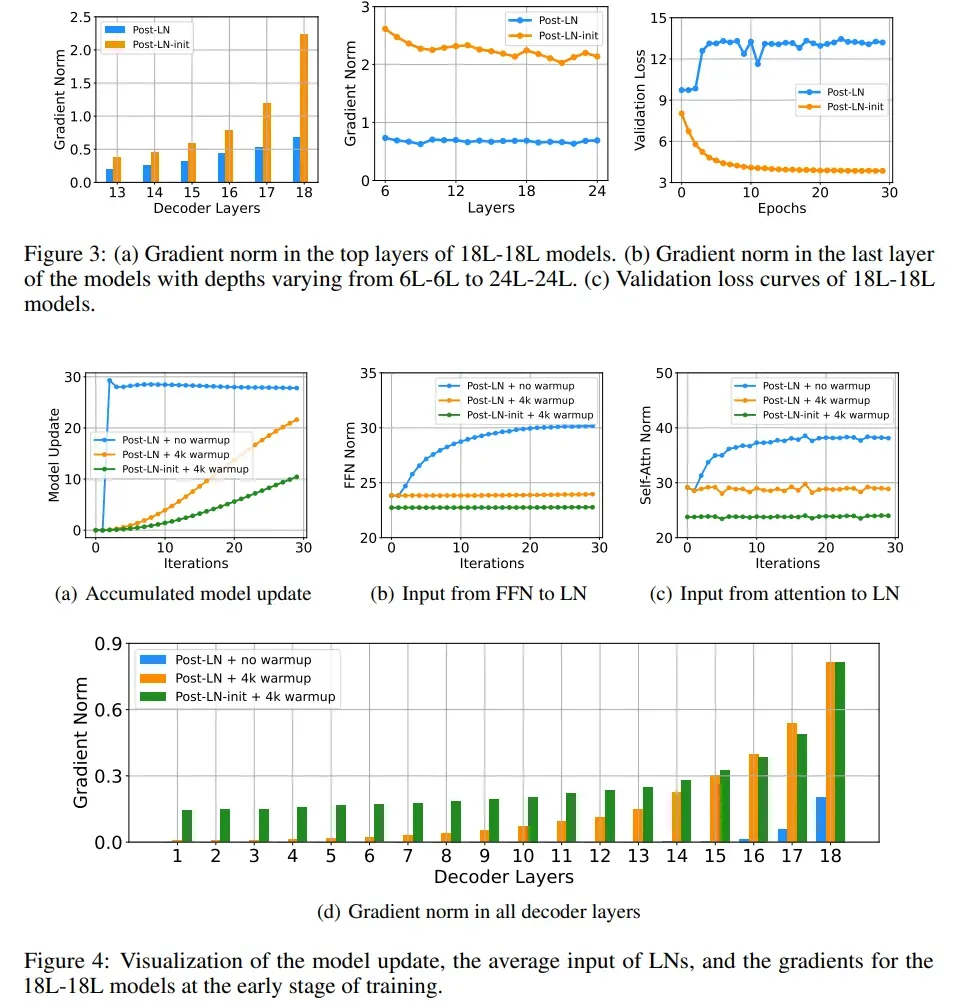
从图3-b可以看出,调整了初始化之后,模型会在顶层获得更大的梯度,但是从图3-a可以看到,虽然其梯度绝对值会变大,但是随着梯度的回传,下层的梯度不会发生爆炸,而是会逐渐收敛的。
事实上,同样的结论可以从图4-d中看出,可以看到,如果不使用Post-LN-init,那么模型的梯度随着反向传播的深入会出现梯度弥散,虽然warmup可以一定程度抑制上述现象的发生,但是随着层数的增加依然无法避免其出现。
具体表现到训练上面,就是模型的顶层会快速地收敛到一个local minimum,而下层的参数很难得到一个很好的训练,这个结果从图3-c以及图4-a中都能够得到印证。
更进一步的,如果打印出layernorm的输入随着训练步数的变化(图4-b以及图4-c)可以看到Post-LN-init更可以令其输入保持在一个相对比较小的值,而原始的初始化方法则更倾向于收敛到一个比较大的输入上面。
而根据文献On Layer Normalization in the Transformer Architecture,layer normalize的梯度大小与其输入模长的反比是在一个量级的(),因此输入的模长越大,梯度也就会越小。
这个结论印证了上图4-d中的结论。
综上所述,我们最终得出结论:
- 传统的transformer参数初始化下的模型梯度会随着的深度的增加快速地发生梯度弥散,从而导致下层无法得到很好的训练,模型陷入到一个local minimum当中,导致效果变差;
- 通过warmup或者调整参数初始化可以优化这个问题,文中提出的 Post-LN-init 就是一个可行的参数初始化优化方案。
3. DeepNorm考察
在检查了参数初始化之后,我们来看看模型的训练过程。
文中同样是先提出了一种DeepNorm的方法,然后再证明了这个方法的有效性。
具体关于这个DeepNorm是什么,其实也简单,就是在LayerNorm的基础上对input进行一下加权,具体而言,就是:
其中,对于attention layer,就是attention函数,对于ffn layer,
就是ffn函数。
文中通过3个定理给出了模型参数改动的上限,然后通过调整超参的方式来对其进行限定,使之不会超过一个常数。
这里的推导还是有些繁琐的。坦白说,我懒得去查计算,所以我只是把文中的结论拿来如下:
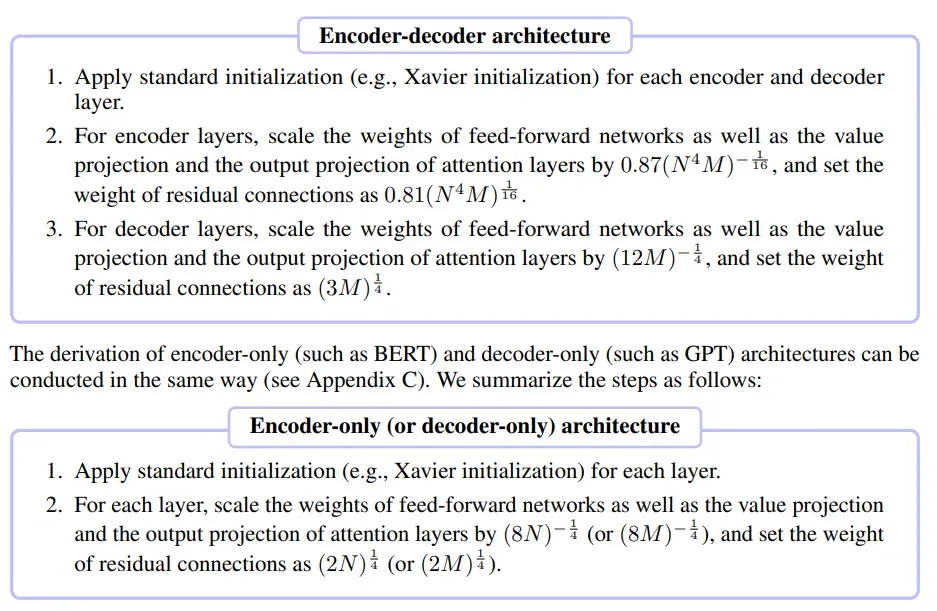
这个事实上图2当中已经有了,不过在这里重新给出一下,毕竟这个是全文的核心。
同样,将模型参数在不同深度的变化打印在论文中,以验证上述推论。
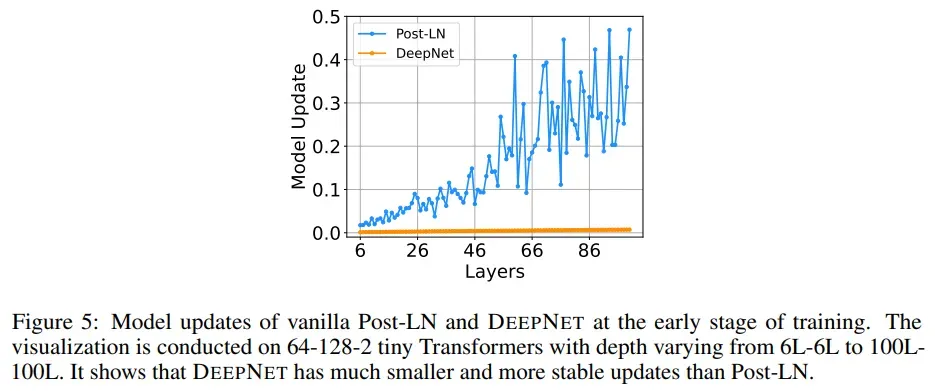
可以看到,使用了DeepNet之后,模型的参数变化就变的平稳和缓慢的了,由此,模型原则上也就能够获得一个长期的训练,而不是快速地陷入到一个local minimum当中。
3. 实验考察
1. 可行性考察
实验方面,首先我们来看一下是否真的DeepNet能够做到在深层模型上面的训练,给出文中实验结果表格如下:
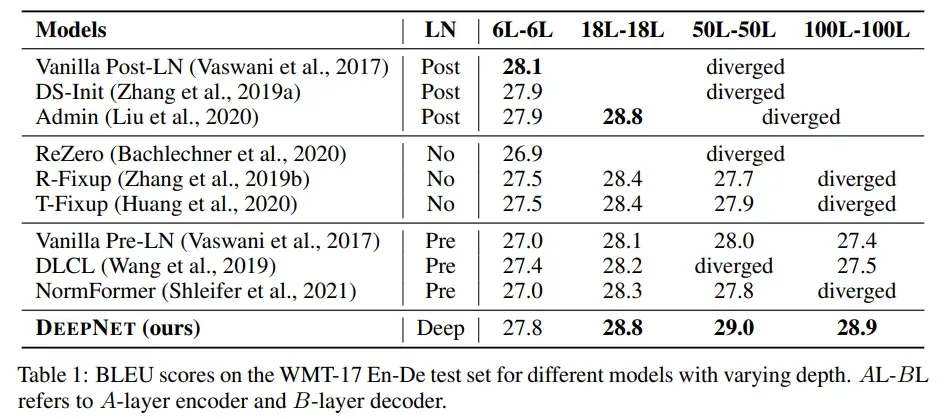
看得见:
- 对于100层的transformer网络,大多数模型都已经失去了效果,不过DeepNet依然可以训练,并且在18层以上的深度都达到了最优的效果。
更进一步的,文中还给出了不同层数下翻译任务中各个模型BLEU指标的变化以及DeepNet的loss随着训练步数增加而发生的变化。
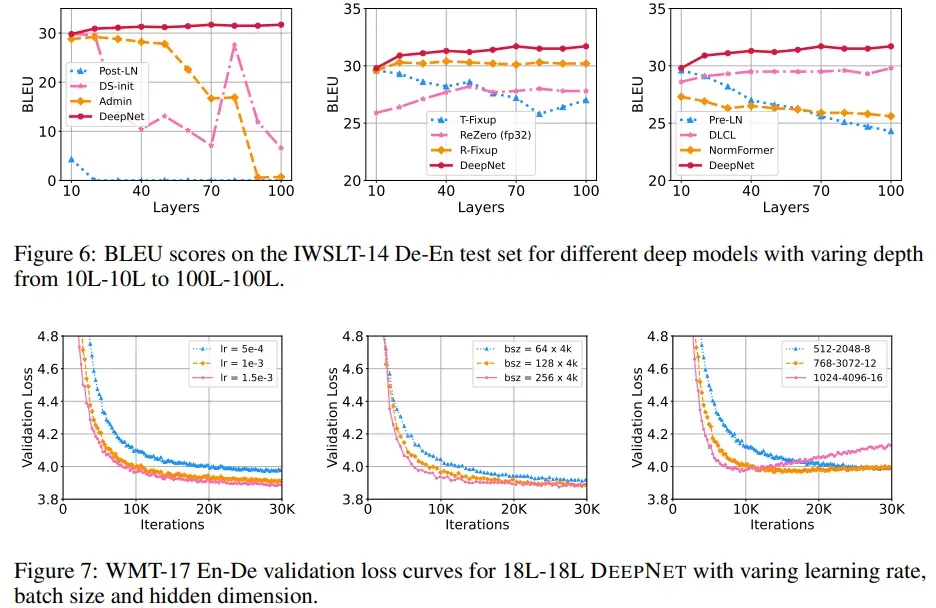
从上图6中可以看到,不同的模型随着深度的增加都会出现一些效果的下滑,只有DeepNet效果一直坚挺,且随着深度的增加还会有效果的收益。
而从图7可以看到,DeepNet广泛地适用于不同配置下的transformer模型,是一个足够general的方法。
2. 有效性考察
最后,我们来看一下deepnet的有效性考察,这个其实在上面的表1当中也能够看到,deepnet模型随着深度的增加是能够带来效果收益的。
而为了更加深入的证明这一点,文中给出了深度为1000的模型在翻译任务当中的效果。
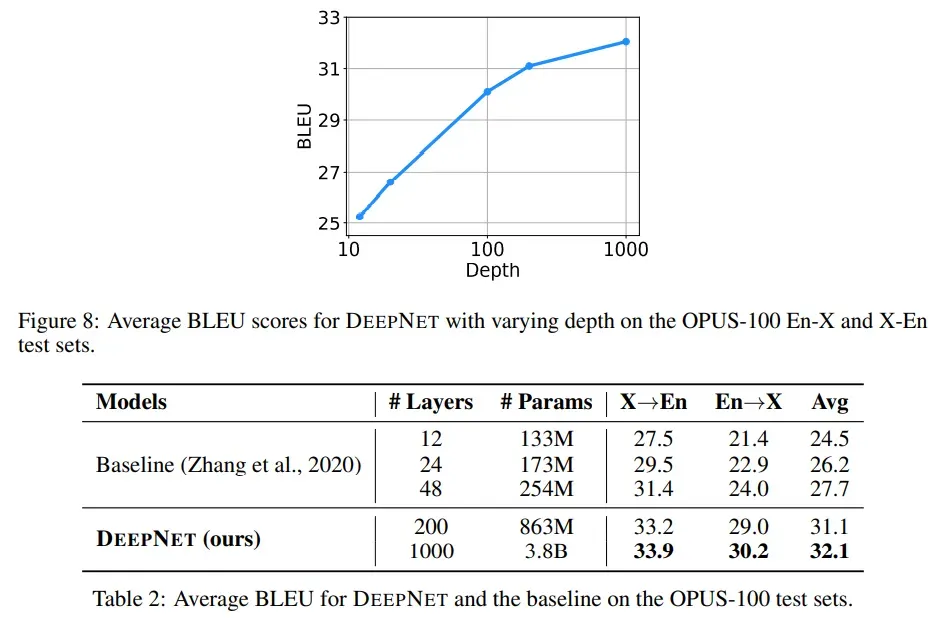
可以看到,200层的模型就已经达到了sota的效果,1000层的模型甚至还能获得更好的效果。
而在其他的翻译任务当中,DeepNet同样是有效的。

4. 结论 & 思考
综上,个人认为文中最主要的贡献就在于说是研究了一下transformer为什么在深层的网络当中会失效(梯度弥散),然后确实地给出了一种可行解使得transformer不仅在深层网络结构下面可以正常训练,并且还能够成功产生收益。
个人觉得这个还是值得借鉴的,虽然1000层网络本身噱头大于用处,不过光是稳定性训练本身就足够对于后续的基于transformer相关的工作提供一定的优化方向了。
文章出处登录后可见!
