在写LSTM之前呢,不得不吐槽甄姬三个技能都带水,还不明白什么意思吗,啊?这个傻鸟下水道英雄我看哪个蠢驴还在一楼拿。
二、LSTM
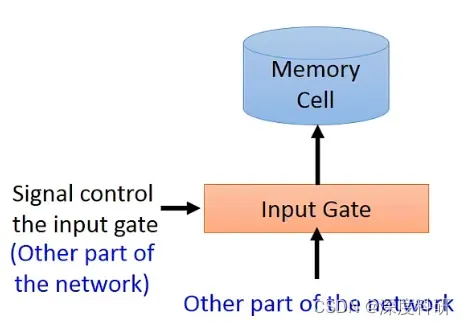
在(一)里面写的呢都是非常原始简单的RNN,每一个输入都会被memory记住。现在RNN的标准做法基本上已经是LSTM。LSTM是一个更加复杂的设计,最简单的设计是每一个neuron都有四个输入,而一般的NN只有一个输入。在(一)里面提到RNN的memory,其实这个memory是最单纯的,为什么这么说呢?因为我们随时都可以把值存到memory里面去,也可以随时呢把值从memory里面读出来。但现在比较常用的memory呢,称之为Long Short-term Memory。这种Long Short-term 的memory呢它的简写就是我们熟知的LSTM——长短期记忆。这种Long Short-term 的memory呢是比较复杂的,它有3个gate,当neural的某个output想要写到memory里面的时候呢,它必须先通过一个闸门——input gate。这个input gate它要被打开的时候,你才能够把值写到memory cell里面去;如果input gate被关起来的时候,其他neuron就没有办法把值写进去。那至于这个input gate是打开还是关闭,这个是要我们的neural network自己学。所以neural network它可以自己学说,什么时候要把input gate打开,什么时候要把input gate关闭。
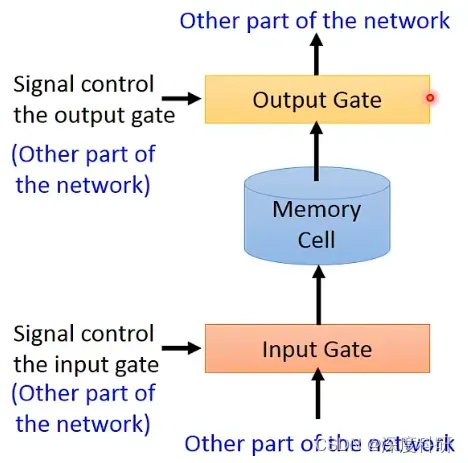
相应地,输出的地方有一个叫做output gate的东西,那这个output gate会决定过说,其他的neuron可不可以从这个memory里面把值读出来。同样地,当output gate被关闭的时候,就没有办法把值给读出来,output gate被打开的时候才能够把值给读出来。跟input gate一样,output gate是打开还是关闭,network是可以自己学出来。
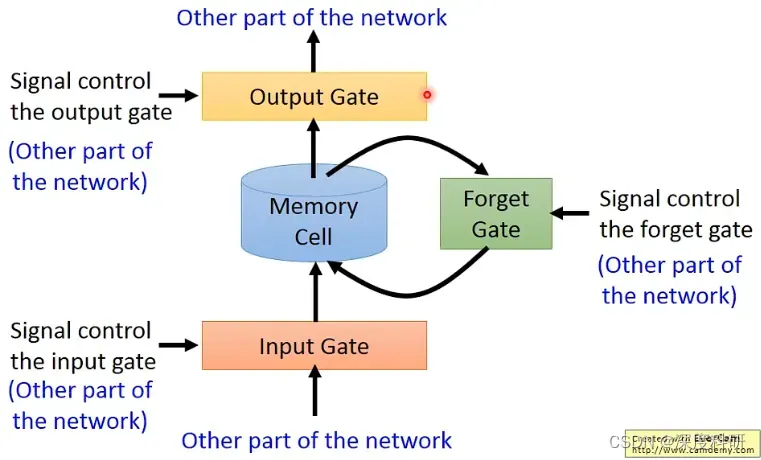
第三个gate呢叫做forget gate。 forget gate决定说什么时候memory cell呢要把过去记得的东西format掉,抑或是存在memory cell里面的值继续保留下来。那是format掉memory cell里面的值还是保留,这个呢同样是network自己学出来的。
所以整个LSTM呢有4个input,1个output。那这4个input是什么呢?这4个input是:①想要被存到memory cell里面的值(但是它不一定存的进行,这取决于说input gate要不要这个information过去)、②操控input gate打开还是关闭的讯号;③操控output gate的讯号;④以及操控forget gate的讯号。
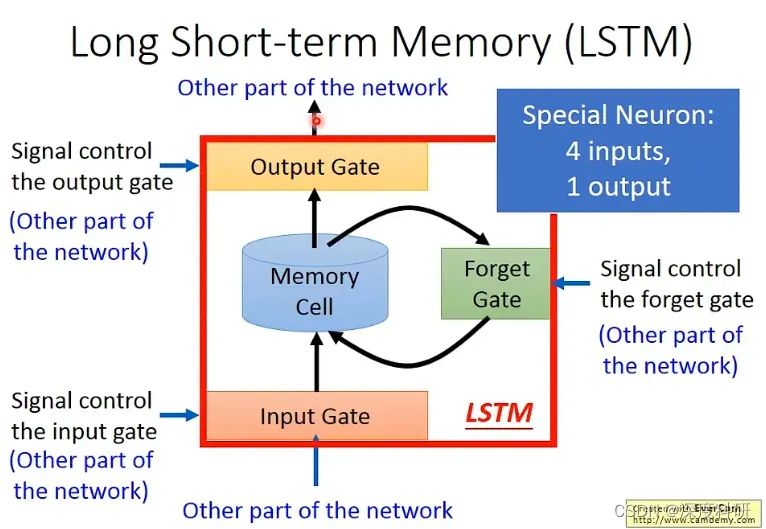
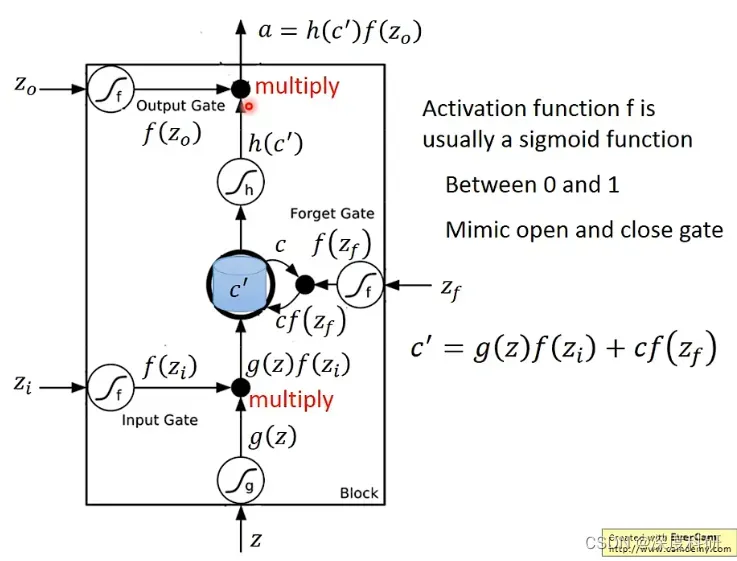
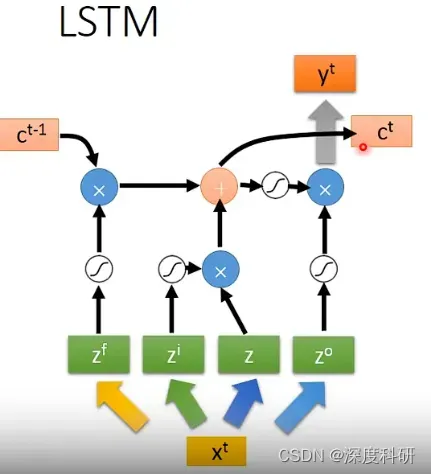
那LSTM的更具体的结构长什么样呢?它就长下面这样。那我们假设呢,现在要被存到cell里面的input叫做,操控input gate的signal叫做
,这个所谓操控input gate的signal其实就是一个scalar(标量)。那你会说这个scalar是从哪里来的呢?看下去可能就就明白了。反正就是说现在有一个数值被当作input gate的input。操控forget gate的数值叫做
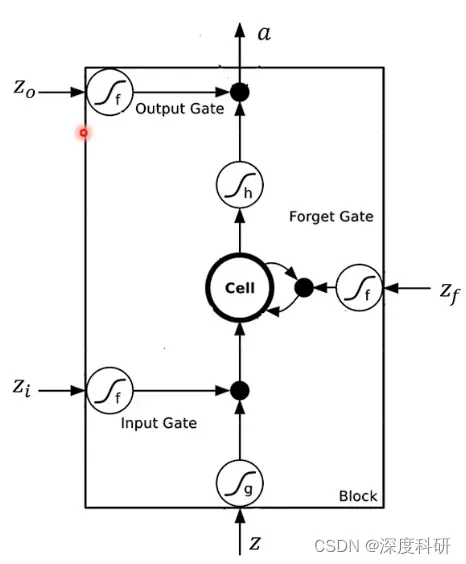
现在,我们假设在有这四个输入之前,cell里面已经存了一个值。现在要输入
,三个gate呢分别是由
、
、
所操控的,那我们的输出
会长什么样子呢?从图中可以看到,我们把
呢通过一个activation function,得到
;然后把
通过另外一个activation function,得到
;要说明的是,图中的这几个activation function通常我们会选择sigmoid function。选择sigmoid function的意义是sigmoid的值是介于0~1之间的,而0~1之间的值代表了这个gate打开与否:如果经过activation function后的值是1,那代表说这个gate是出于被打开的状态;反之呢代表这个gate是被关闭的。接下来呢,我们就把
与
相乘,得到
。forget gate的signal
也通过sigmoid activation function得到
。紧接着,我们把存在memory里面的值
,乘上
,得到
,然后与
相加得到
,即
。
就是新的存在memory cell里面的值。所以到目前为止,我们可已发现说,
就是控制
可不可以输入的一个关卡。因为假设
,那
就等于0,这就意味着没有输入一样;如果
,那就相当于直接输入
。同理,
就决定说我们要不要把存在memory cell里面的值format掉,因为假设
,那
就等于0,这意味着forget gate是被关闭的,过去存在memory里面的值呢就会被format掉变成0;如果
,forget gate是被打开的, 那
等于1,过去存在memory里面的值被保留下来。forget gate的开关呢跟我们的直觉好像是相反的,forget gate打开的时候代表的是“记得”,它被关闭的时候,代表的是“遗忘“。然后我们把
和
相加起来,写到memory里面得到
。之后,我们把
通过sigmoid activation function,得到
。在这边呢,有一个output gate,它受
所操控。
通过sigmoid activation function得到
,然后与
相乘得到
=
。显然,如果
是0的话,output gate被关闭,那
就等于0,这表示说我的
无法输出;如果
是1的话,output gate被打开,相当于直接输出
.
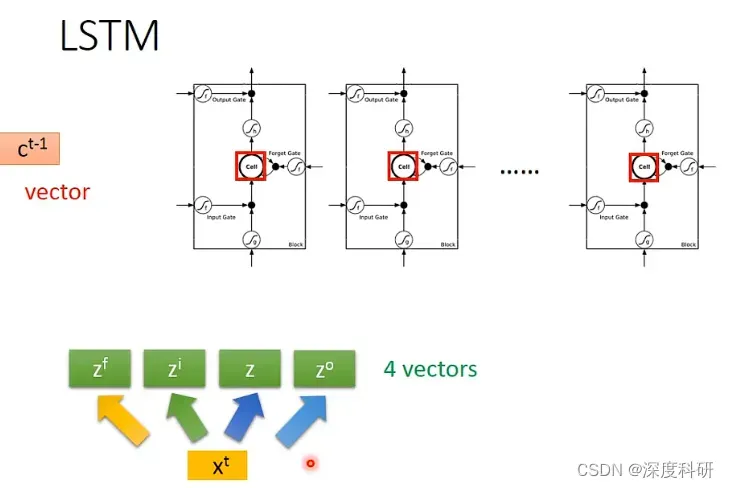
假设我们现在有一整排的LSTM,假设这一整排的LSTM里面它们每一个的memory cell里面都预先存了一个scale,把所有的scale接起来,它们就变成一个vector,这里用来表示。也就是说vector
里面的某一个dimension就代表了某个cell里面的scale。现在在时间点
,input一个vector
,
首先会被乘上一个linear的transform,也就说
会被乘上一个矩阵,变成vector
。说明一下的是,下图中的粗箭头代表的就是说乘上一个linear的transform,希望你不会有所诧异。那
这个vector代表什么呢?向量
里面的每一个dimension呢,就代表了操控每一个LSTM的input。所以向量
的dimension正好是LSTM的memory cell的数目,那
的第一维就丢给第一个LSTM的input,第二维就丢给第二个LSTM的input,以此类推。那向量
呢会再乘上一个matrix得到向量
,
的dimension也跟LSTM的memory cell的数目一样,
的每一个dimension都会去操控每一个LSTM的input gate。那forget gate和output gate分别由
、
的每一维所操控,那
、
也是向量
乘上一个matrix所得到的,这里就不再赘述。综上所述,我们把
乘上四个不同的matrix得到四个不同的vector,这4个vector的dimension都跟LSTM的memory cell的数目是一样,这4个vector的dimension的每一维都控制着不同gate的输入。
那我们现在知道,一个LSTM的输入分别是、
、
和
。需要强调的是,这四个输入都是vector,都到LSTM里面的值呢其实只是每一个vector里面的一个dimension,因为每一个LSTM input的dimension都是不一样的,所以每个LSTM output的值呢也会是不一样的。但是所有的LSTM cell是可以共同被运算的,怎么一起共同被运算呢?我们说
要通过activation function跟
相乘,这里的相乘是element-wise的product的意思。
要通过activation function跟预先存在memory cell里面的值(也就是下图中
)相乘后,再与
通过activation function跟
相乘的值相加。
通过activation function与之前的output相加以后的结果相乘,得到最后的输出
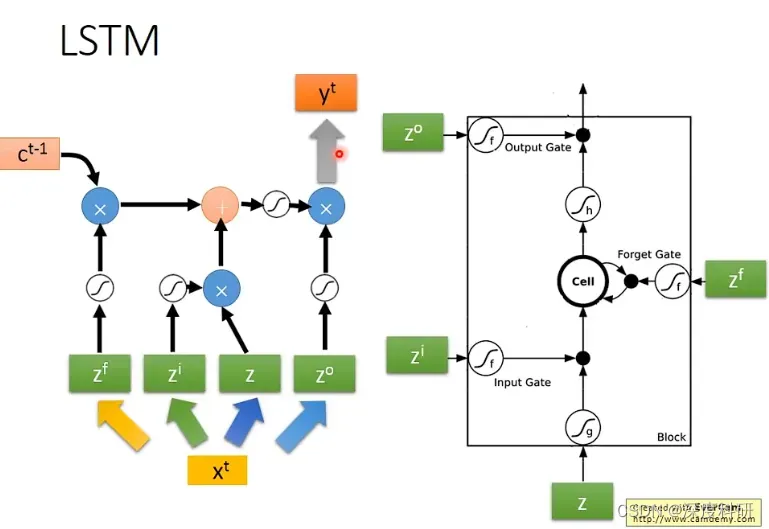
在上图中,相加以后的结果,就是存在memory cell里面的值
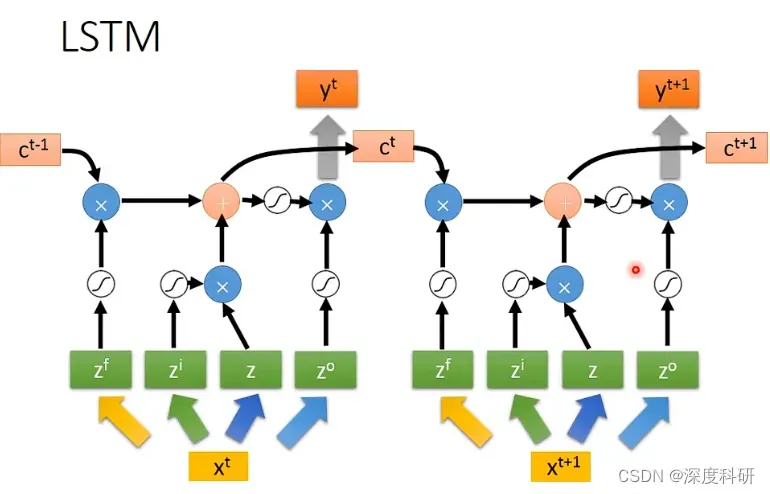
那这个process就反复的进行下去,在下一个时间点 input …
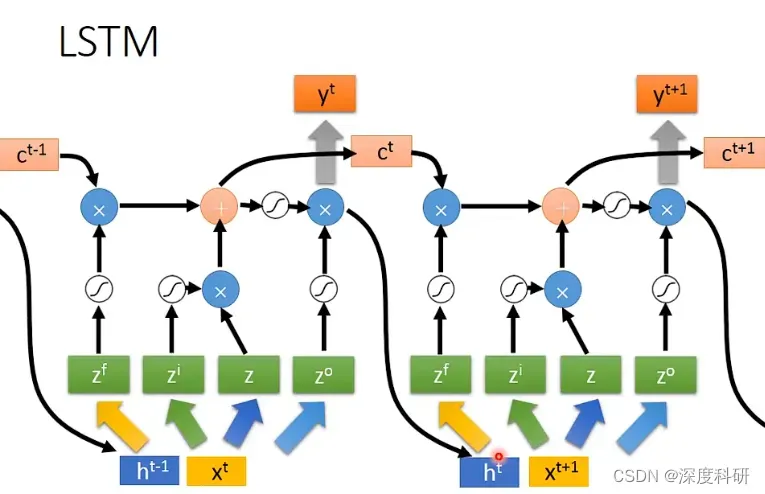
在LSTM中还会把蓝色部分的输出接到输入,形成更复杂的结构…
参考:李宏毅机器学习视频李宏毅2021/2022春机器学习课程
文章出处登录后可见!
