一、设计要求
-
熟悉并掌握MATLAB中有关声音(wave)录制、播放、存储和读取的函数;
-
在MATLAB环境中,使用声音相关函数录制2秒左右自己的声音,抽样率是8000Hz;
-
分别取8000个和16000个数据进行频谱分析,得到幅度和相位谱,比较二者异同并分析原因;
-
针对电话信道(最高3500Hz),设计一个FIR或IIR滤波器进行滤波,把抽样率转变为7000Hz,并进行频谱分析,得到幅度和相位谱;
-
把处理后的所有数据储存为声音文件,与原始声音进行比较。
二、 原理简介
1.MATLAB中声音获取
- 录制:
recObj = audiorecorder(fs,8,2),抽样率fs, 8位数据,2通道,recObj为audiorecorder类。
recordblocking(recObj,2),录2秒 钟
- 播放
play(输入参数为audiorecorder类) 或 sound(输入参数为语音信号数据,向量或矩阵形式,还要输入抽样率)
- 存储
y = getaudiodata(recObj), 获取时域语音信号数据y,向量或矩阵形式, 以后处理都用这个数据
audiowrite(‘原始录音.wav’,y,fs)
- 读取
[y,fs] = audioread('原始录音.wav');
2. 降采样
M倍的降采样,时域下每隔M1个点抽取一个点形成新的信号;频域下频谱扩展了M倍,周期仍为2π,幅度变为原来的1/M.
3. 滤波
IIR滤波器
IIR的冲击响应h[n]为无限长。根据所要设计滤波器的参数去确定一个模拟滤波器的传输函数H(s),然后再根据这个传输函数,通过双线性变换、或脉冲响应不变法来进行数字滤波器的设计。
选用巴特沃斯滤波器。巴特沃斯滤波器的特点是通带内的频率响应曲线最大限度平坦,没有起伏,而在阻带则逐渐下降为零。
巴特沃斯低通滤波器可用如下振幅的平方对频率的公式表示:
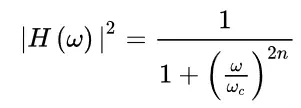
其中,n为滤波器的阶数,ωc为截止频率,即振幅下降为3分贝时的频率。
设计时需要指定通带边界频率wp(归一化的),阻带边界频率ws,通带的波纹系数Rp, 阻带最小衰减Rs. 调用MATLAB函数buttord可自动计算出巴特沃斯滤波器的参数:阶数N, 截止频率wc. 见如下命令。
[N,wc]=buttord(wp,ws,Rp,Rs)
[num,den]=butter(N,wc) 该命令可以生成传递函数的分子num与分母den的系数向量。
yf=filter(num,den,y) 将滤波器作用于语音时域数据y,得到滤波后的yf.
FIR滤波器
FIR的冲击响应h[n]为有限长。使用窗函数法设计时域的系统函数h[n]。理想的h[n]为无限长sinc函数,需要加窗来限定为有限长,于是频域下变为有过渡带,阻带有波动的滤波器。选的窗不同,阻带最小衰减不同。
MATLAB命令 num=fir1(N,wc) 指定阶数N, 截止频率wc, 可生成Hamming窗的传递函数系数num
IIR, FIR的选择
从性能上来说,IIR滤波器传递函数包括零点和极点两组可调因素,对极点的惟一限制是在单位圆内。因此可用较低的阶数获得高的选择性,所用的存储单元少,计算量小,效率高。但是这个高效率是以相位的非线性为代价的。选择性越好,则相位非线性越严重。FIR滤波器传递函数的极点固定在原点,是不能动的,它只能靠改变零点位置来改变它的性能。所以要达到高的选择性,必须用较高的阶数;对于同样的滤波器设计指标,FIR滤波器所要求的阶数可能比IIR滤波器高510倍,结果,成本较高,信号延时也较大;如果按线性相位要求来说,则IIR滤波器就必须加全通网络进行相位校正,同样要大大增加滤波器的阶数和复杂性。而FIR滤波器却可以得到严格的线性相位。
从使用要求上来看,在对相位要求不敏感的场合,如语言通信等,选用IIR较为合适,这样可以充分发挥其经济高效的特点;对于图像信号处理,数据传输等以波形携带信息的系统,则对线性相位要求较高,如果有条件,采用FIR滤波器较好。
三、实验步骤
-
用MATLAB录音2秒(抽样率8000),存储声音文件,获得时域音频数据y. 编写了record函数,输出音频数据y。
-
将y做fft变换,画出幅度(abs)和相位(angle)谱。取y的8000个数据(2倍降采样)做fft变换,画出幅度和相位谱。编写了process_draw(y)函数,音频数据y作为输入参数。
-
重新录制抽样率为7000的语音。设计IIR 巴特沃斯低通滤波器,对语音进行处理。
利用freqz函数画出滤波器的频谱图,画出语音信号处理前后的频谱图。为了更好展现滤波效果,幅值使用对数坐标,单位分贝,MATLAB公式:20*log10(abs(Y))
其中Y为fft的结果。
播放、存储处理后的语音。编写了yf=process_filter(y)函数,输入为处理前语音数据y,输出为处理后语音数据yf.
四、结果分析
1.录音结果
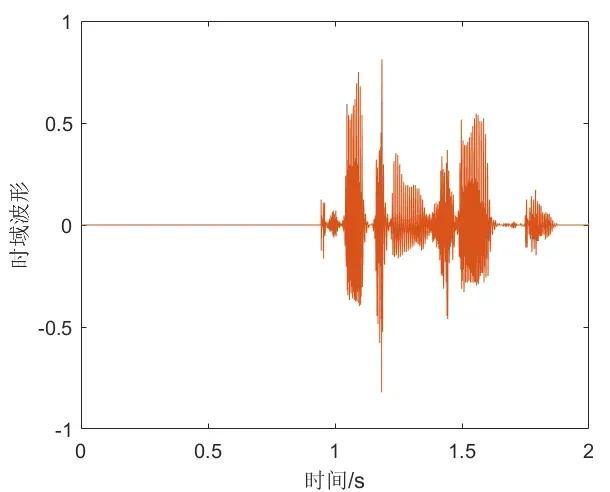
采用双通道录音,效果会比单通道好。上图为时域波形数据,双通道的数据几乎重合。录音时,开始的1秒无法录入语音。
2. 分别取8000个和16000个数据进行频谱分析
录音的抽样率为8000Hz,录音2秒,总共得到16000个数据点。取8000个数据点进行频谱分析,相当于对音频进行2倍的降采样。
绘制频谱图时,频率轴采用归一化的数字频率,截取fft变换的前半部分显示,对应数字角频率0π。因为频谱是关于π对称的。
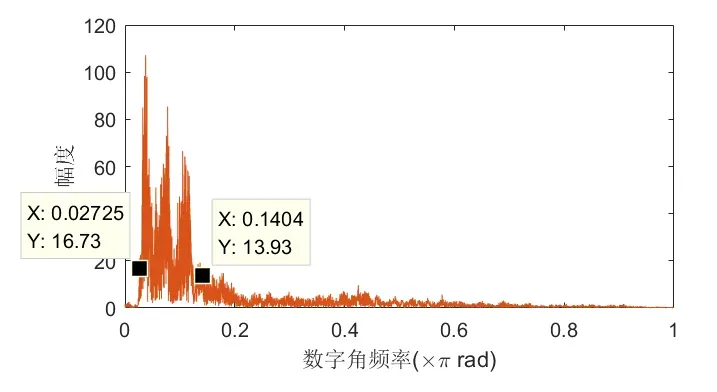
上图结果显示,语音信号的幅度集中在0.03π至0.14π之间,对应模拟频率为0.034000=120Hz到0.144000=560Hz之间。
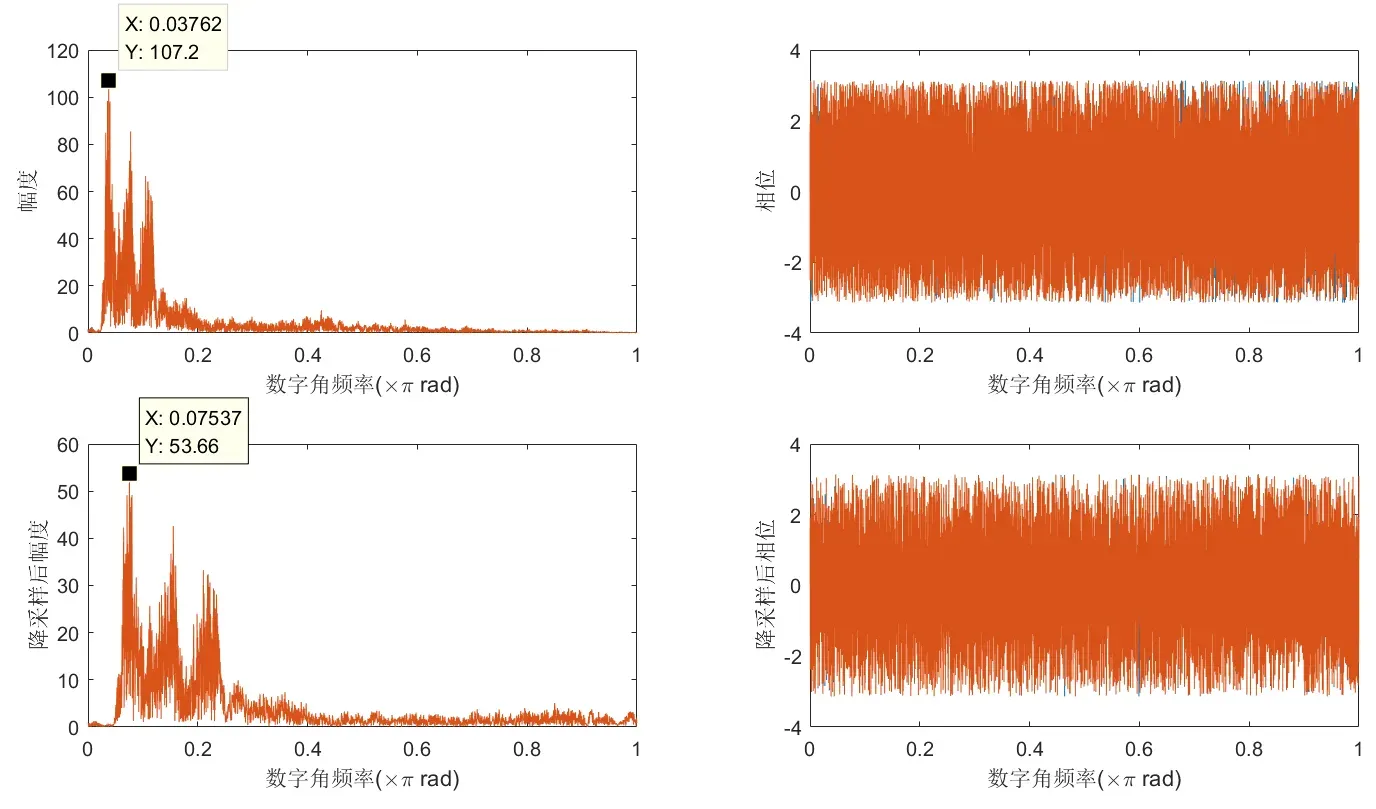
上图为2倍降采样前后频谱的对比,可见幅度近似变为了原来的0.5倍,而频率近似扩展到原来的2倍,符合理论预期。结果并不是完全精确的理论的倍数,因为原信号在数字频率0.5以上仍有微小的幅度分量,2倍降采样后,该部分会造成混叠。
3. 抽样率转变为7000Hz进行录音,进行低通滤波
- IIR滤波器
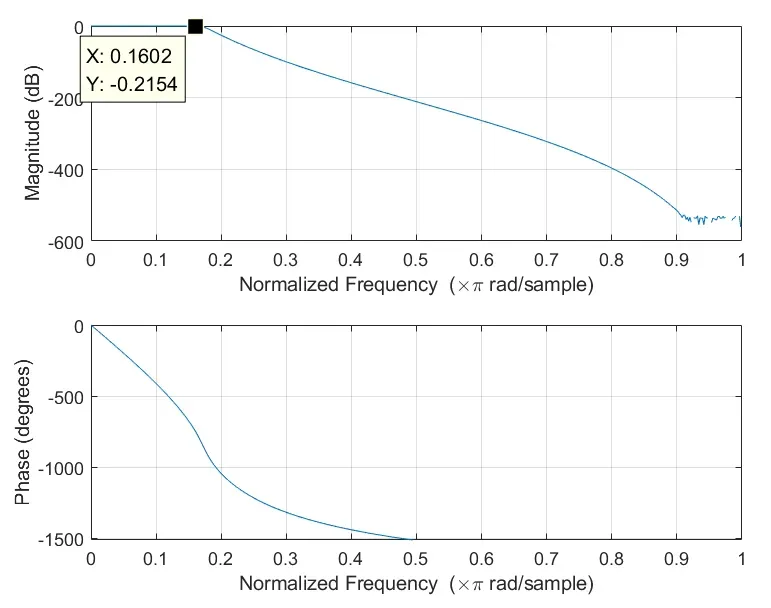
上图为巴特沃斯滤波器的频谱图,滤波器参数为:通带边界频率ωp=0.16π,阻带边界频率ωs=0.3π,通带的波纹系数Rp=0.42, 阻带最小衰减Rs=100dB。语音滤波前后的幅度谱(分贝)和相位谱见下图。可见0.2π左右幅度大幅衰减。
播放滤波后的语音信号,发现声音更加低沉,因为滤掉了高频成分。
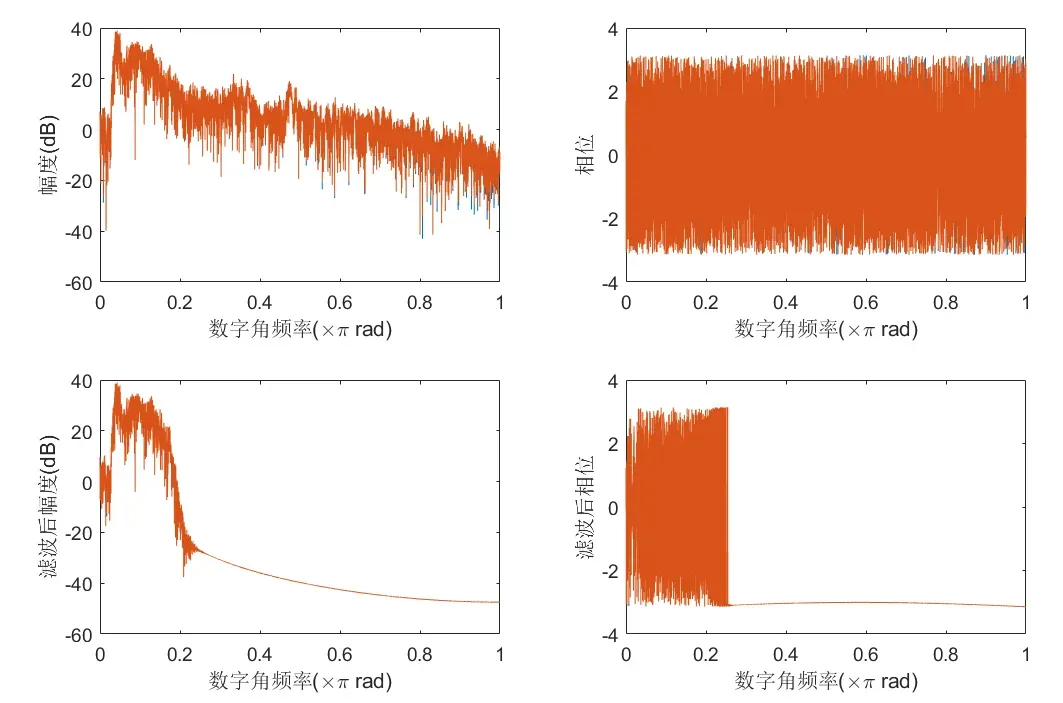
- FIR滤波器
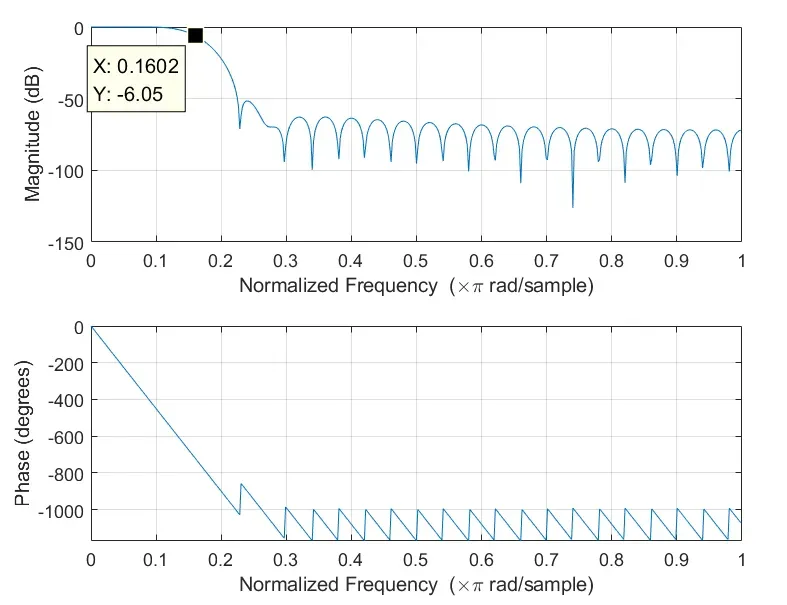
上图为N=50, 截止频率0.16π的Hamming窗的幅度相位频谱图,可见在00.2π范围内为线性相位。
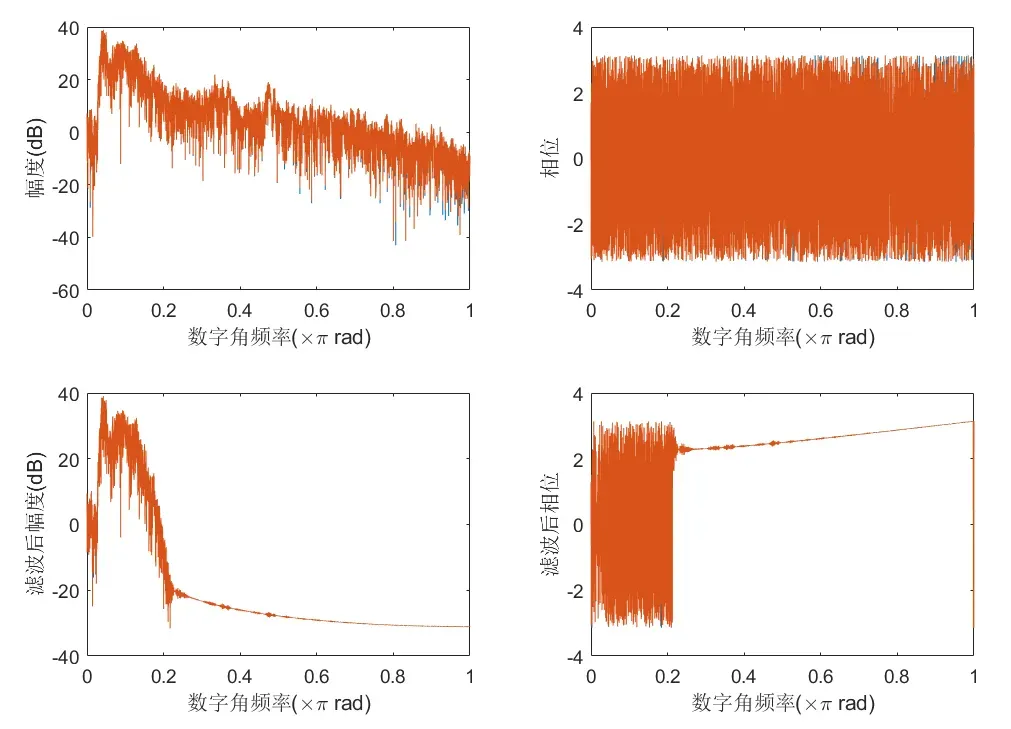
上图为滤波前后的幅度谱(分贝)和相位谱。可见0.2π以后衰减至20dB以下。
播放滤波后的语音信号,发现声音更加低沉,因为滤掉了高频成分。
五、 补充内容
为了更好地验证滤波器的效果,对原始音频加单频噪声,即时域数据加上一个cos信号,其频谱为单频的脉冲。下图为加了噪声后的时域波形,可见几乎完全将原始语音信号覆盖。
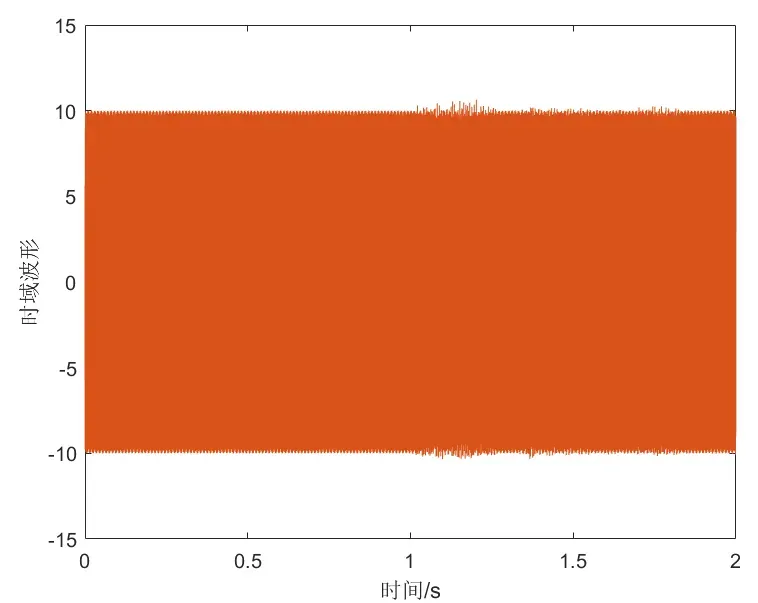
再使用IIR滤波,滤波器参数与上面相同
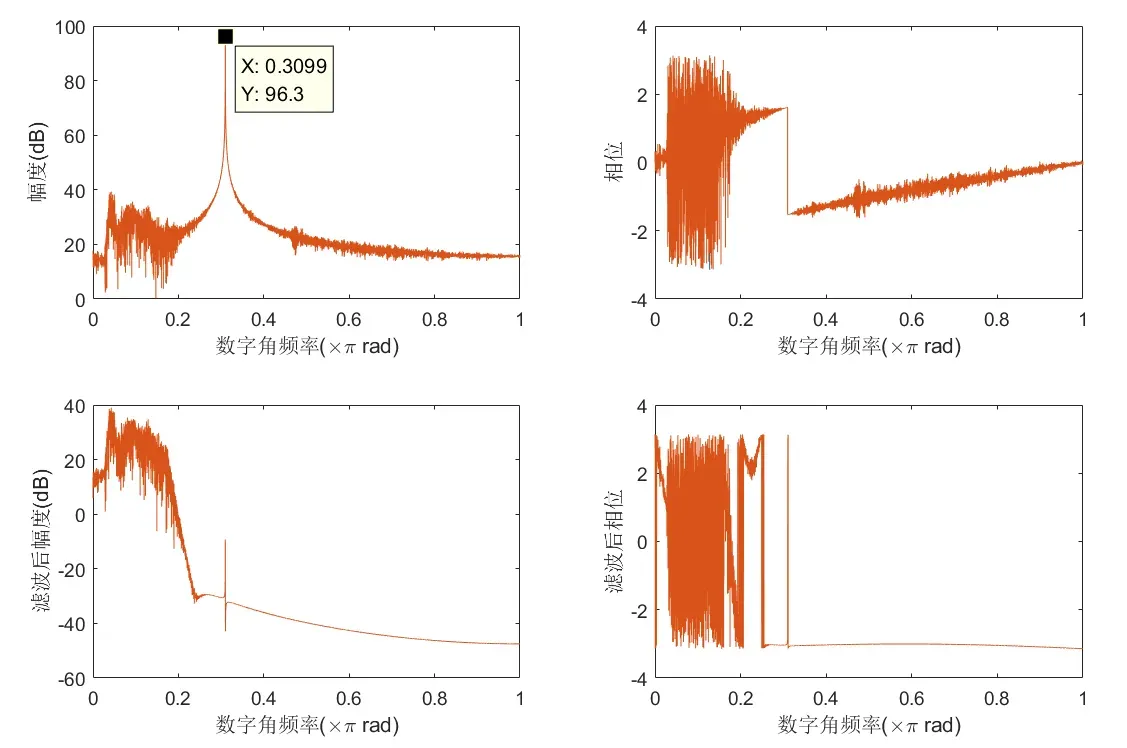
滤波前后频谱图见上图。可见0.3π左右加了一个单频噪声,播放录音时完全将语音盖住。滤波后,该噪声的幅度大幅度衰减,播放音频,不会再听到噪音。
六、附录
代码:
有四个函数文件:record, process_draw, process_filter, add_noise
运行示例,命令行依次输入:

Hz抽样率录音,画频谱图)

Hz抽样率录音,滤波)

(加噪声后滤波)
function y=record()
close all
fs=7000;
%取样频率
duration=2;
%录音时间2s
disp('按任意键开始录音')
pause
recObj = audiorecorder(fs,8,2);
%抽样率fs 8位数据 2通道
disp('开始录音')
recordblocking(recObj, duration);
% 录音录2秒钟
disp('结束录音');
% 回放录音数据
play(recObj);
% 获取录音数据
y = getaudiodata(recObj);
audiowrite('原始录音.wav',y,fs)
function process_draw(y)
%y为两通道,16000*2
close all
fs=8000;
%取样频率
duration=2;
%录音时间2s
t=linspace(0,duration,duration*fs);
% 绘制录音数据波形
figure
plot(t,y);
xlabel('时间/s')
ylabel('时域波形')
n=size(y,1);
%n 采样点个数
f=(0:n/2-1)/n*2;
%归一化的数字频率 前一半频谱
fd=f(2:2:end);
yd=y(2:2:end,:);
%抽取一半 降采样
Y=fft(y);
Yd=fft(yd);
Y=Y(1:n/2,:);
%画出前一半频谱,角频率0-pi
Yd=Yd(1:n/4,:);
figure
subplot(221)
plot(f,abs(Y))
xlabel('数字角频率(\times\pi rad)')
ylabel('幅度')
subplot(222)
plot(f,angle(Y))
xlabel('数字角频率(\times\pi rad)')
ylabel('相位')
subplot(223)
plot(fd,abs(Yd))
xlabel('数字角频率(\times\pi rad)')
ylabel('降采样后幅度')
subplot(224)
plot(fd,angle(Yd))
xlabel('数字角频率(\times\pi rad)')
ylabel('降采样后相位')
function yf=process_filter(y)
close all
%下面为IIR巴特沃斯滤波器设计
wp=0.16;
%通带边界频率
ws=0.3;
%阻带
Rp=0.42;
%通带波纹系数
Rs=100;
%最小阻带衰减
[N,wc]=buttord(wp,ws,Rp,Rs)
[num,den]=butter(N,wc);
%下面为FIR hanning滤波器设计
% N=50;
% wc=0.16;
% num=fir1(N,wc);
% Hamming window
% den=1;
%FIR滤波器传递函数分母为1
figure(1)
freqz(num,den)
yf=filter(num,den,y);
%滤波后
sound(yf,7000)
audiowrite('IIR滤波后.wav',yf,7000)
n=size(y,1);
%n 采样点个数
f=(0:n/2-1)/n*2;
%归一化的数字频率 前一半频谱
Y=fft(y);
Yf=fft(yf);
Y=Y(1:n/2,:);
%画出前一半频谱,角频率0-pi
Yf=Yf(1:n/2,:);
figure(2)
% 绘制滤波前后频谱
subplot(221)
plot(f,20*log10(abs(Y)))
xlabel('数字角频率(\times\pi rad)')
ylabel('幅度(dB)')
subplot(222)
plot(f,angle(Y))
xlabel('数字角频率(\times\pi rad)')
ylabel('相位')
subplot(223)
plot(f,20*log10(abs(Yf)))
xlabel('数字角频率(\times\pi rad)')
ylabel('滤波后幅度(dB)')
subplot(224)
plot(f,angle(Yf))
xlabel('数字角频率(\times\pi rad)')
ylabel('滤波后相位')
function yn=add_noise(y)
fs=7000;
n=size(y,1);
%n 采样点个数
%noise=0.1*randn(n,1);
%加白噪声
fn=1000;
n=10*cos(fn*[1:n])';%加单频噪声
noise2=[n n];
yn=y+noise2;
sound(yn,fs)
audiowrite('加单频噪声后录音.wav',yn,fs)
文章出处登录后可见!
