目录

神经网络基础

        在本节中您需要重点记忆的专业术语有：神经元、权重、偏重、阈值、激活函数、输入层、隐藏层、输出层

（一）从感知机到神经网络

1、感知机

        感知机是由美国学者FrankRosenblatt 在1957 年提出来的。为何我们现在还要学习这一很久以前就有的算法呢？因为感知机也是作为神经网络（深度学习）的起源的算法。

        下图是最简单的感知机，x1、x2 是输入信号，y 是输出信号，w1、w2 是权重，图中的○称为“神经元”或者“节点”，输入信号被送往神经元时，会被分别乘以固定的权重（w1x1、w2x2）。神经元会计算传送过来的信号的总和，只有当这个总和超过了某个界限值时，才会输出1。这也称为“神经元被激活” 。这里将这个界限值称为阈值，用符号θ 表示。

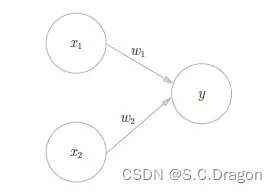
 将上述内容用数学公式可表达为：（权重越大对应的信号重要性就越大）

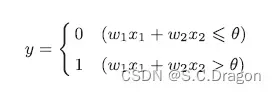
2、基于感知机实现简单逻辑电路

        神经网络的基础也可类似于数字逻辑电路，在这里我们首先用感知机实现简单的逻辑电路（例如：与门）。与门是有两个输入和一个输出的门电路，真值表如下图所示：

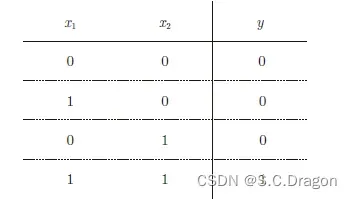
        满足上述条件的权重和阈值有无限多个，例如，当(w1, w2, θ) = (0.5, 0.5, 0.7) 时，可以满足图的条件。此外，当(w1, w2, θ)为(0.5, 0.5, 0.8) 或者(1.0, 1.0, 1.0) 时，同样也满足与门的条件。设定这样的参数后，仅当x1 和x2 同时为1 时，信号的加权总和才会超过给定的阈值θ，从而确定输出的数据。

3、导入权重和偏置

刚才的与门的实现比较直接、容易理解，但是考虑到以后的事情，我们将其修改为另外一种实现形式。在此之前，首先把1、中的数学表达式的θ 换成−b，于是可以用下述式子来表达：

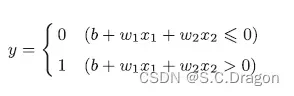
这两个数字虽然只有一个符号不同，但表达的内容是完全相同的。此处，b 称为偏置，w1 和w2 称为权重。

4、感知机的局限性

 异或门电路中，仅当x1 或x2 中的一方为1 时，才会输出1，其真值表如下图所示，我们现在思考一下，我们能否用感知机来实现异或门电路呢？如果能那么它们的权重和偏置又分别为多少呢？

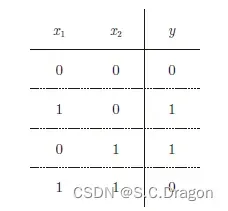
 现在我先给出明确的答案：用感知机不能表达出异或门电路，原因我们现在来探讨：

        首先，我们试着将或门的动作形象化。或门的情况下，当权重参数(b, w1, w2) = (−0.5, 1.0, 1.0) 时，可满足如下图或门真值表的条件

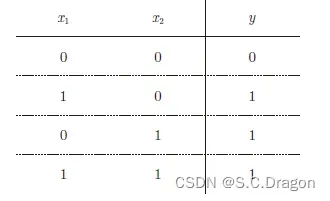
其数学表达式为：

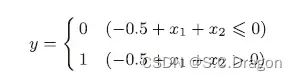
 上述表示的感知机会生成由直线−0.5 + x1 + x2 = 0 分割开的两个空间。其中一个空间输出1，另一个空间输出0。如下图所示：

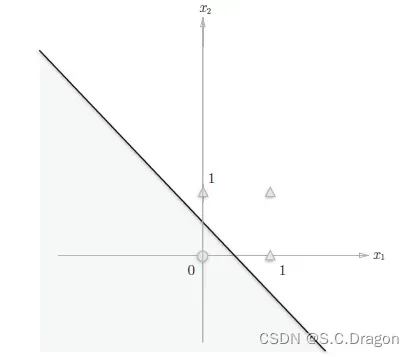
 但换成异或门电路，能否像或门那样子输出呢？答案是不能的，因为上述感知机只能实现线性“分割”，如下图所示的异或门空间就不能用一条直线分割而成，需要用一条曲线（非线性），这也就是感知机的局限所在

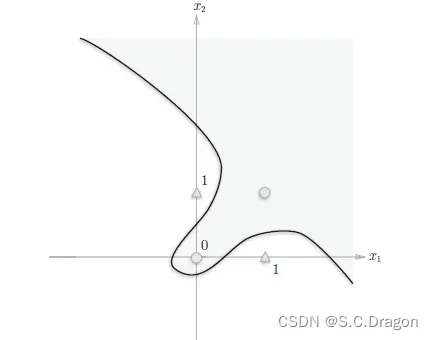
5、多层感知机实现非线性

为了实现非线性，可以使用多层感知机来实现：
如下图所示为组合与门、或门实现异或门的逻辑电路图

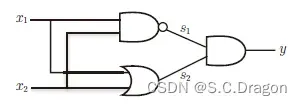
 真值表为：（可以看出完全符合异或门的真值表）

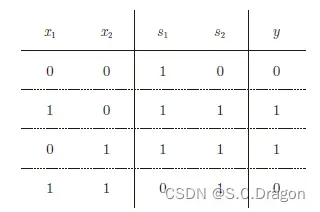
 上述组合门的逻辑电路图可简化成如下图：

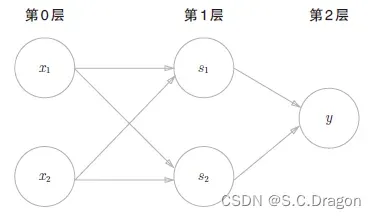
 （ps：看这个组合图是不是又点神经网络内味了，别着急我们马上引出神经网络！）

6、从感知机到神经网络

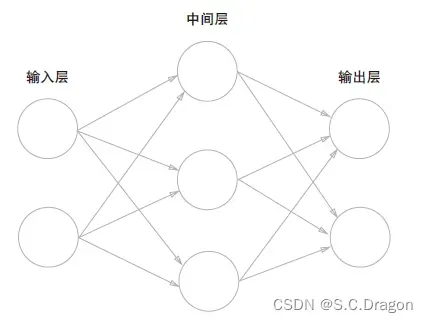
         我们把最左边的一列称为输入层，最右边的一列称为输出层，中间的一列称为中间层，中间层也可称作隐藏层

现在我们把感知机部分中的数学表达式更换一下（为了引出激活函数）

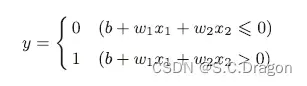
将上述的感知机的数学表达式改写成 y = h(b+w1x1+w2x2)

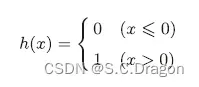
 用神经网络结构图可表示成：

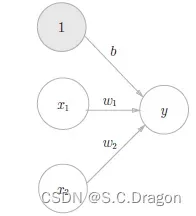
（二）激活函数

1、什么是激活函数

        刚才所说的h（x）函数会将输入信号的总和转换为输出信号，这种函数一般称为激活函数（activation function）。如“激活”一词所示，激活函数的作用在于决定如何来激活输入信号的总和。将上述式子再分解成如下所示：

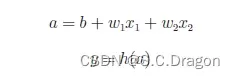
 用神经元来体现激活函数的工作过程：

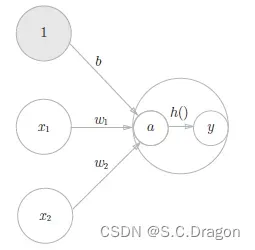
 下面我们将介绍常见的激活函数

 2、Sigmoid函数

数学表达式：

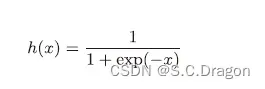
函数大致图像：

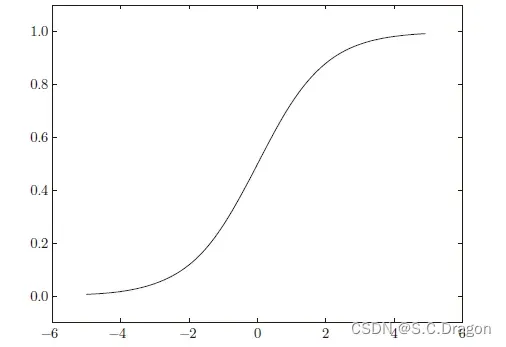
 代码实现：

def softmax(x):
    if x.ndim == 2:
        x = x.T
        x = x - np.max(x, axis=0)
        y = np.exp(x) / np.sum(np.exp(x), axis=0)
        return y.T 

    x = x - np.max(x) # 溢出对策
    return np.exp(x) / np.sum(np.exp(x))

2、ReLU函数

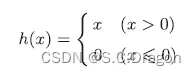
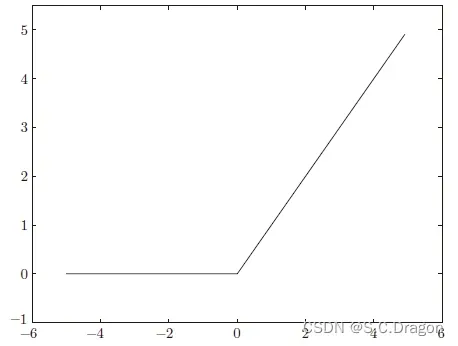
代码实现：

def relu(x):
    return np.maximum(0, x)