投影矩阵的性质
1,投影矩阵不可逆。
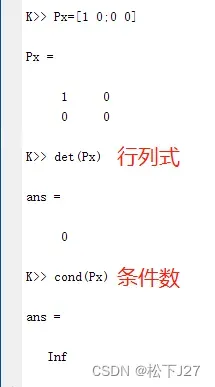
例1:P1,P2分别是可以把二维空间中任意向量投影到x轴和y轴上的两个投影矩阵。

分别计算他们的行列式和条件数,行列式的值为0,条件数无穷大,说明该矩阵不可逆是一个奇异矩阵singular matrix。
例2:三维空间中,可以把任意向量投影到向量a上的投影矩阵P。

同样:行列式的值为0,条件数趋近于无穷大,说明该矩阵不可逆,是一个奇异矩阵singular matrix。

2,投影矩阵是一个对称矩阵。
对称矩阵:就是形如下面的一些矩阵,矩阵沿对角线成镜像对称。
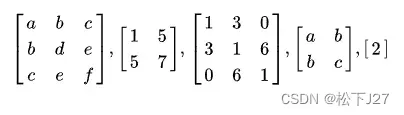
当然,最经典的对称矩阵就是单位矩阵Identity matrix
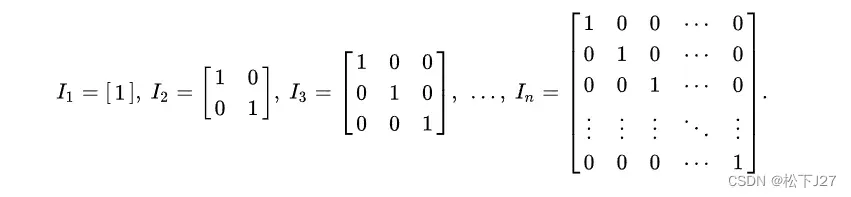
3,对于把任意向量投影到某一个方向的投影矩阵而言,投影矩阵是一个秩为1的矩阵(例如,在由n个线性无关的列向量所张成的n维列空间中,把向量投影到第
个方向上的投影矩阵)。但对于,能够把向量投影到某个平面或子空间上的投影矩阵而言,则不然(例如,在三维空间中,能够把向量投影到x-y平面上的投影矩阵的秩为2)。
任何一个秩等于1的矩阵都可以用如下形式来表示(其中,u,v都是列向量,又因为u,v的维数可以不同,所以,A不一定是方阵):
例如:在图像处理中最常被用来模糊图像的二维高斯核,就是一个秩为1的矩阵。

4, 对于任何投影矩阵P而言,有:
也就是说,无论投影多少次,最终得到的都是同样的投影向量p,即:
这是合理的,因为投影在相同方向的二次投影就是他自己。
5,用相同尺寸的单位矩阵I减投影矩阵P,会得到一个新的投影矩阵I-P,这个新的投影矩阵I-P的投影方向和P的投影方向相互垂直。如果用这个投影矩阵I-P去左乘向量b,得到的正好是垂直于投影向量p的误差向量e,即:
个人学习笔记:


注:笔记中第4条结论有误。
(全文完)
作者 — 松下J27
参考文献(鸣谢):
1,《Introduction to Linear Algebra》,5th Edition – Gilbert Strang
2,线性代数及其应用,侯自新,南开大学出版社,1990.
3,https://en.wikipedia.org/wiki/Identity_matrix
外国优秀哲理诗词赏析:


(配图与本文无关)
版权声明:所有的笔记,可能来自很多不同的网站和说明,在此没法一一列出,如有侵权,请告知,立即删除。欢迎大家转载,但是,如果有人引用或者COPY我的文章,必须在你的文章中注明你所使用的图片或者文字来自于我的文章,否则,侵权必究。 —-松下J27
版权声明:本文为博主作者:松下J27原创文章,版权归属原作者,如果侵权,请联系我们删除!
原文链接:https://blog.csdn.net/daduzimama/article/details/127908063
