线性代数最被低估的一个事实:矩阵是图,图是矩阵。
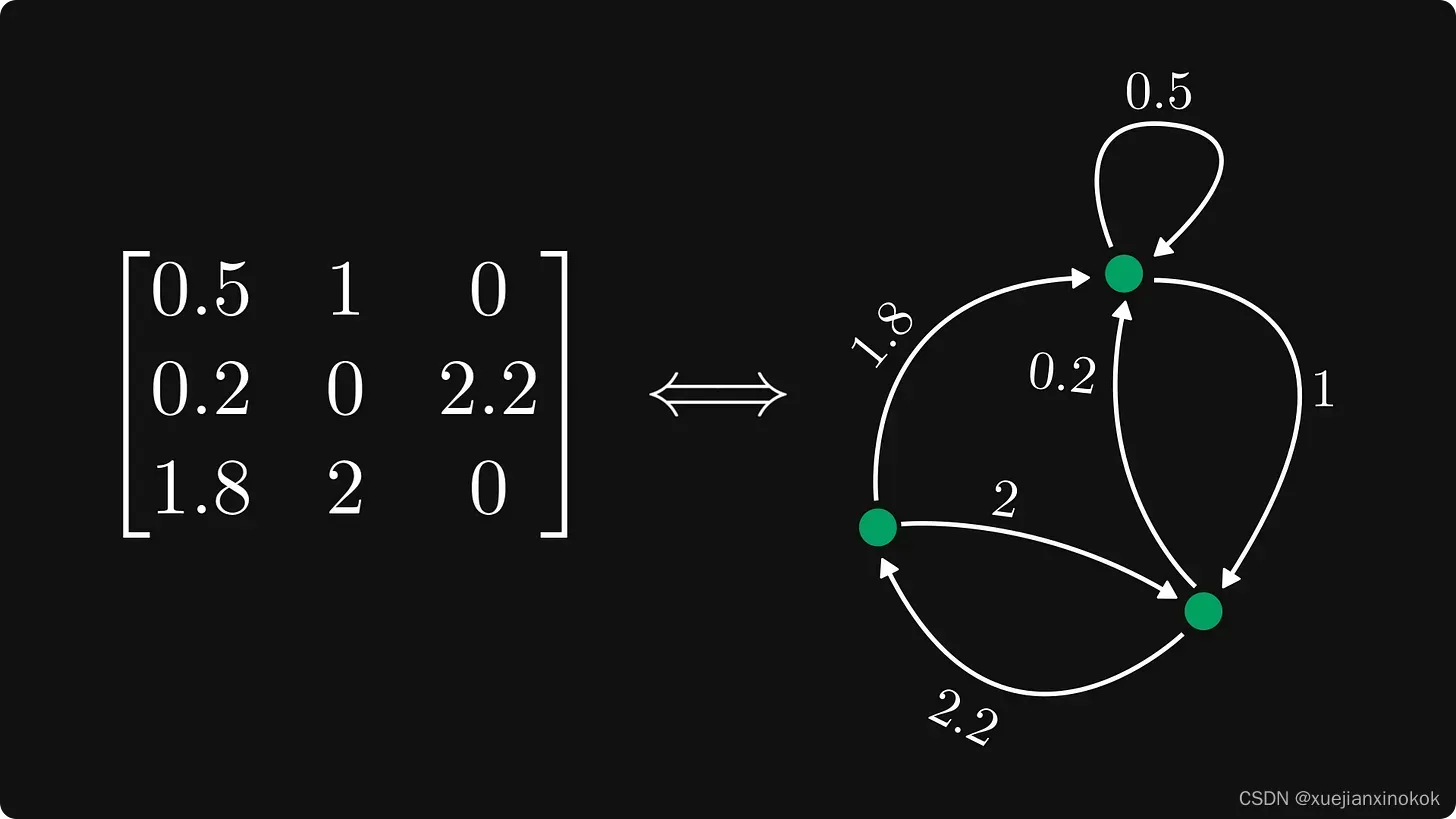
将矩阵编码为图是一种取巧的行为(cheat code),它其使复杂的行为变得易于研究。
让我告诉你怎么做!
1. 非负矩阵的有向图 (The directed graph of a nonnegative matrix)
如果你看了上面的例子,你可能就明白了这个规则。
每一行都是一个节点,每个元素代表一条有向加权边。零元素的边被省略。第 i 行第 j 列中的元素对应于从 i 到 j 的一条边。
得到的图称为矩阵的有向图(或有向图)。
为了稍微展开一下定义,让我们检查第一行,它对应于从第一个节点传出的边。
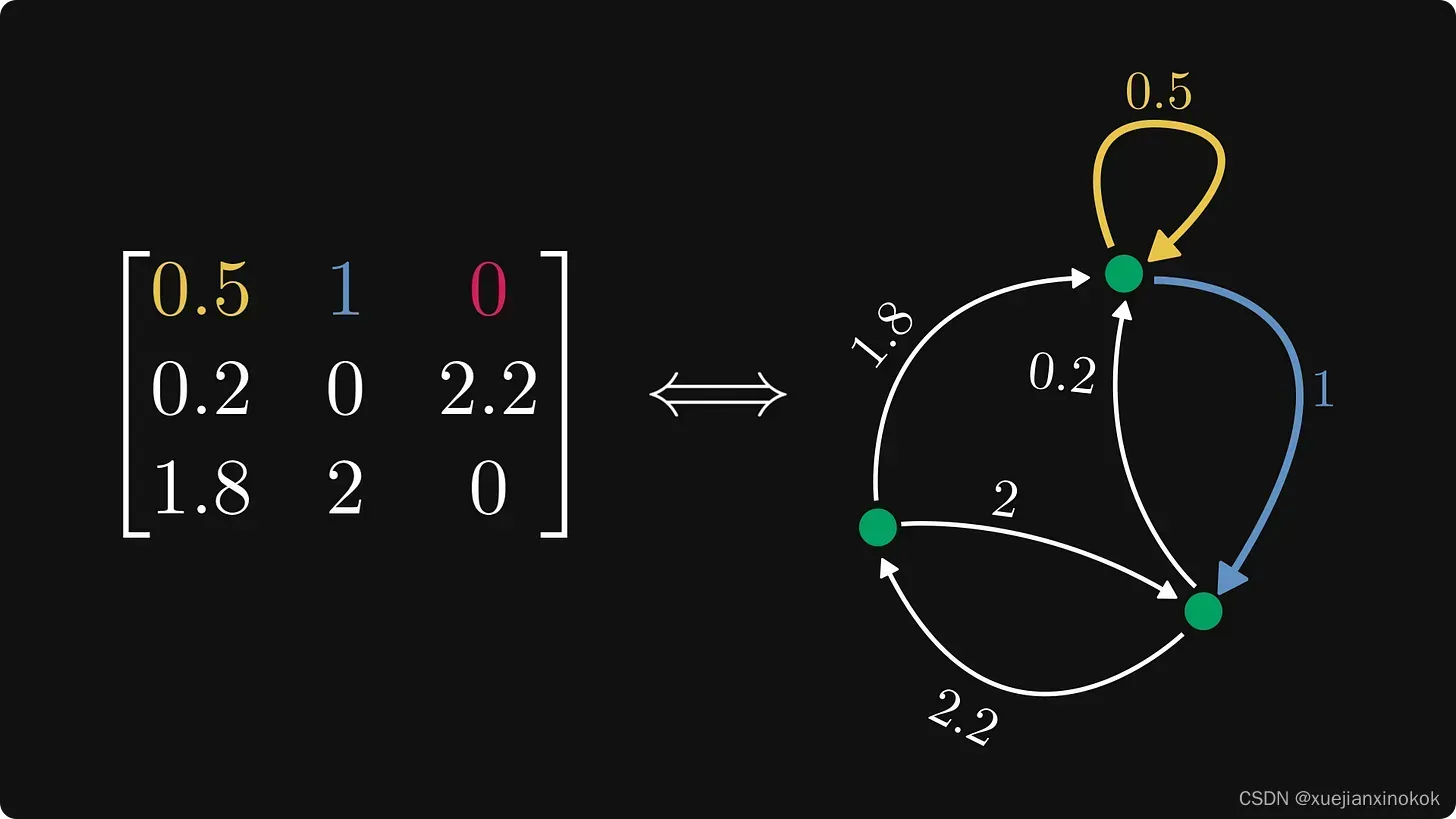
第一行对应于从第一个节点传出的边
类似地,第一列对应于传入第一个节点的边。

第一列对应于传入第一个节点的边
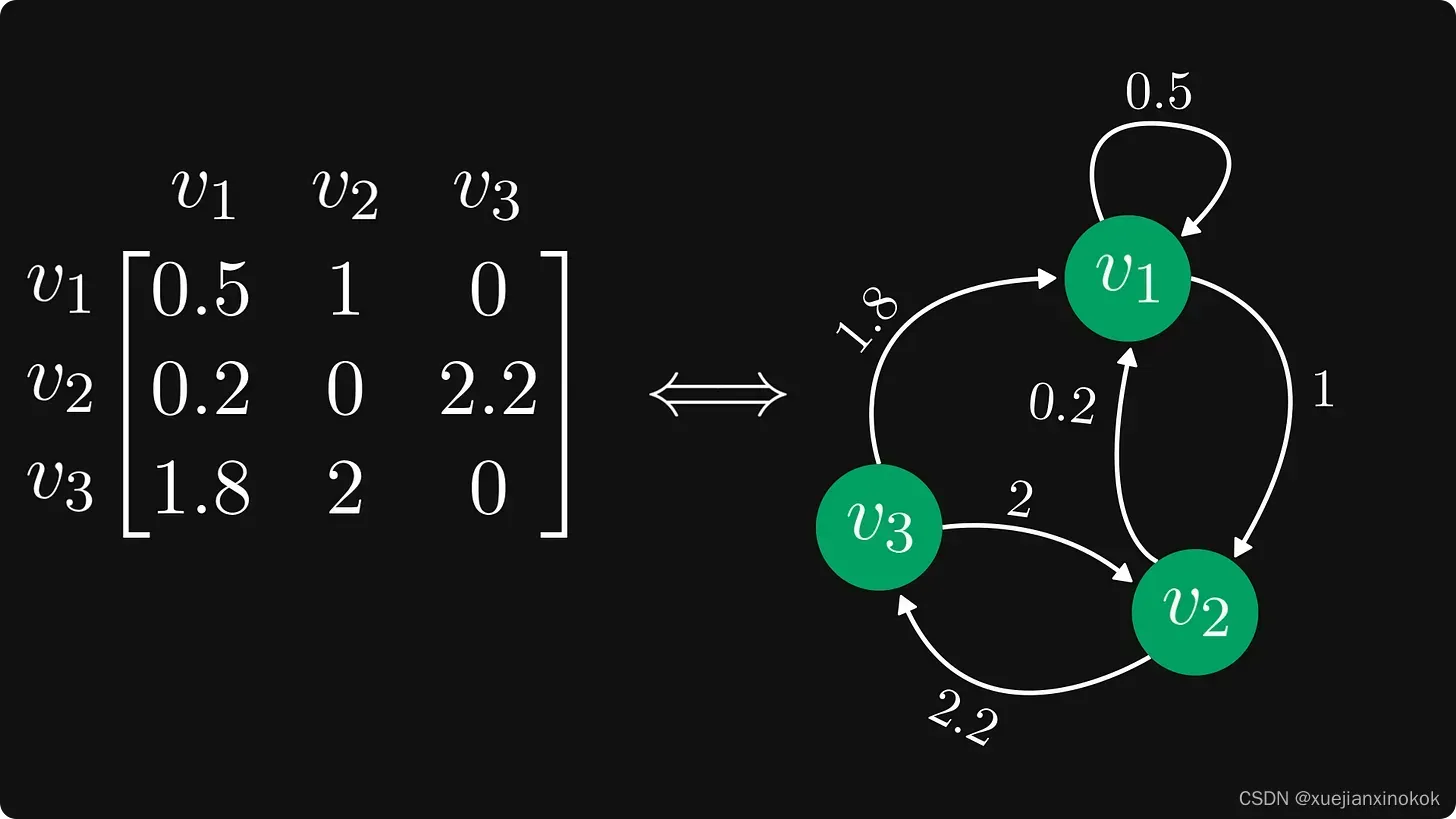
这是完整的图片,节点被明确标记。
2. 图表示的好处(Benefits of the graph representation)
为什么有向图表示对我们有益?
其一,矩阵的幂对应于图中的转移(the powers of the matrix correspond to walks in the graph)。
看一下方阵的元素。所有可能的 2 步 转移(2-step walk)均计入定义 A² 元素的总和中。
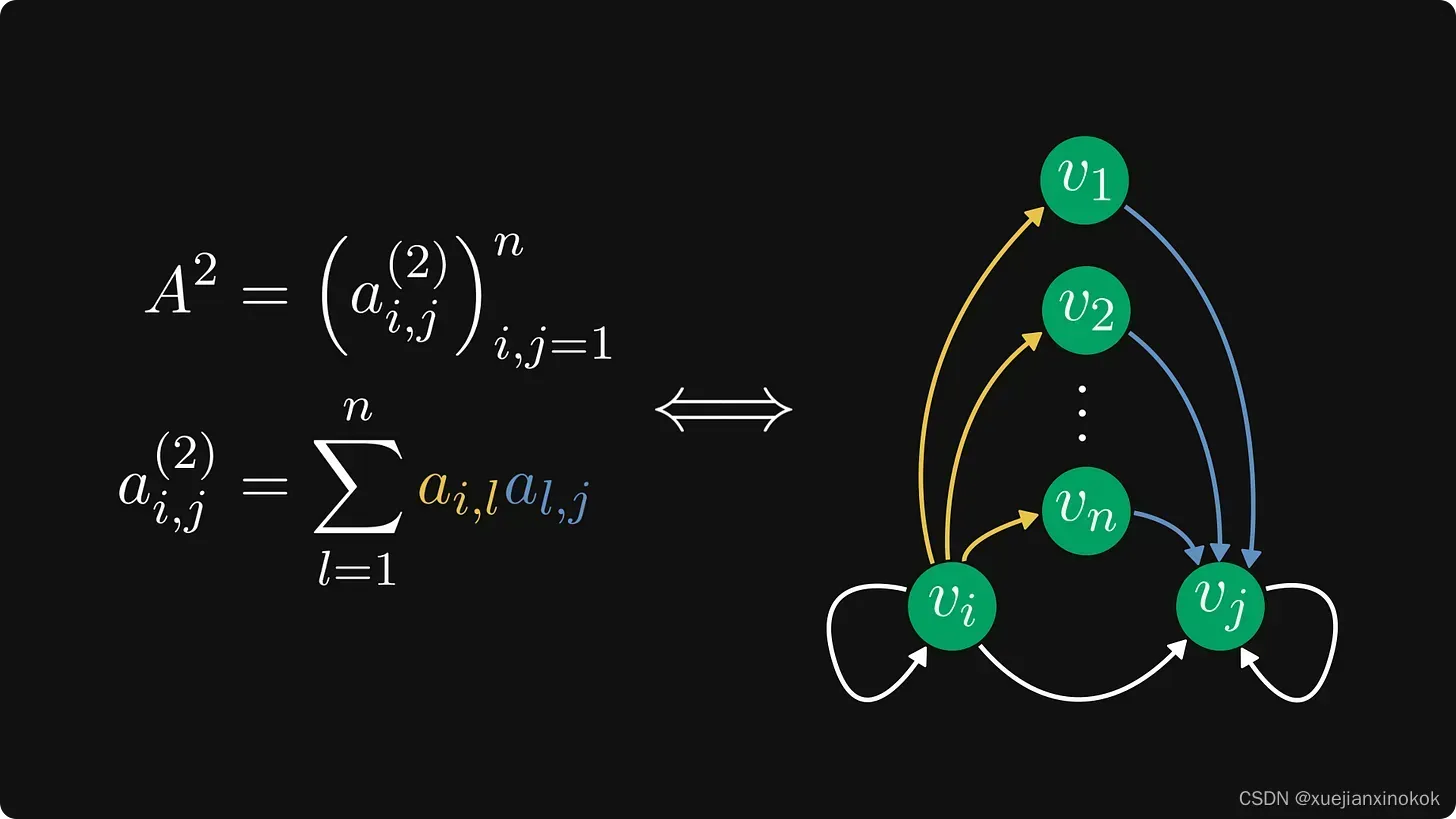
如果有向图表示马尔可夫链的状态,则其转移概率矩阵的平方本质上表示该链在两步后具有某种状态的概率。
.
这种联系还有更多内容。
例如,它让我们深入了解非负矩阵的结构。
为了了解图表示为矩阵的情况,我们来讨论一下强连通分量的概念。
3. 图的连通性(The connectivity of graphs)
如果每个节点都可以从每个其他节点到达,则有向图是强连通的。
如果这不成立,则该图不是强连通的。
下面,您可以看到两者的示例。

对应于强连通图的矩阵称为不可约矩阵。所有其他非负矩阵都称为可约矩阵。很快,我们就会知道原因。(判断矩阵是否是一个不可约矩阵还有一个等价方式,就是看矩阵对应的有向图是否是强连通图)

(为简单起见,我假设每条边都有一个单位权重,但现实中每个权重可以是任意非负数。)

回到一般情况!
尽管并非所有有向图都是强连通的,但我们可以将节点划分为强连通的 子组件。
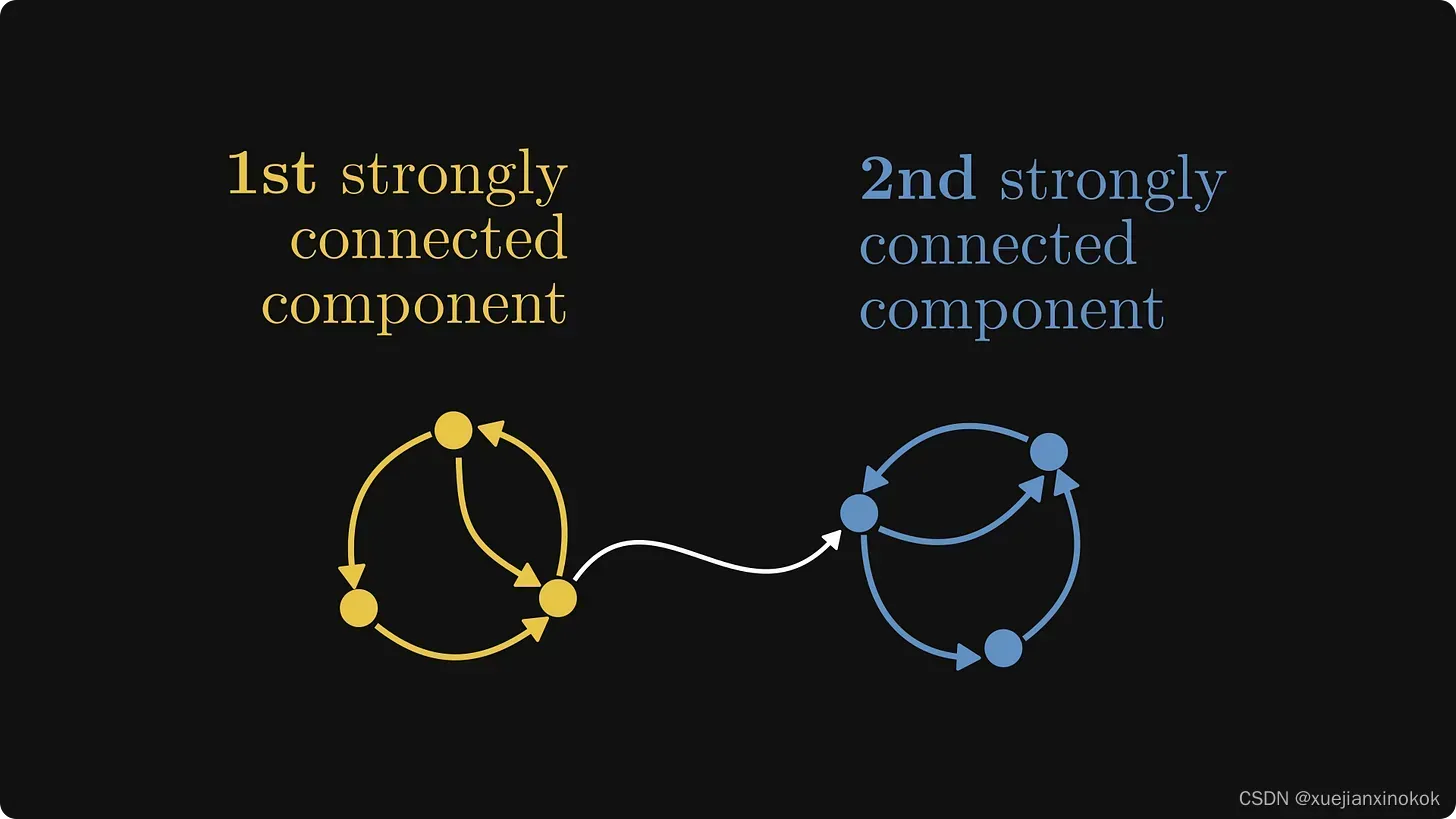
让我们标记这个图的节点并构造相应的矩阵!
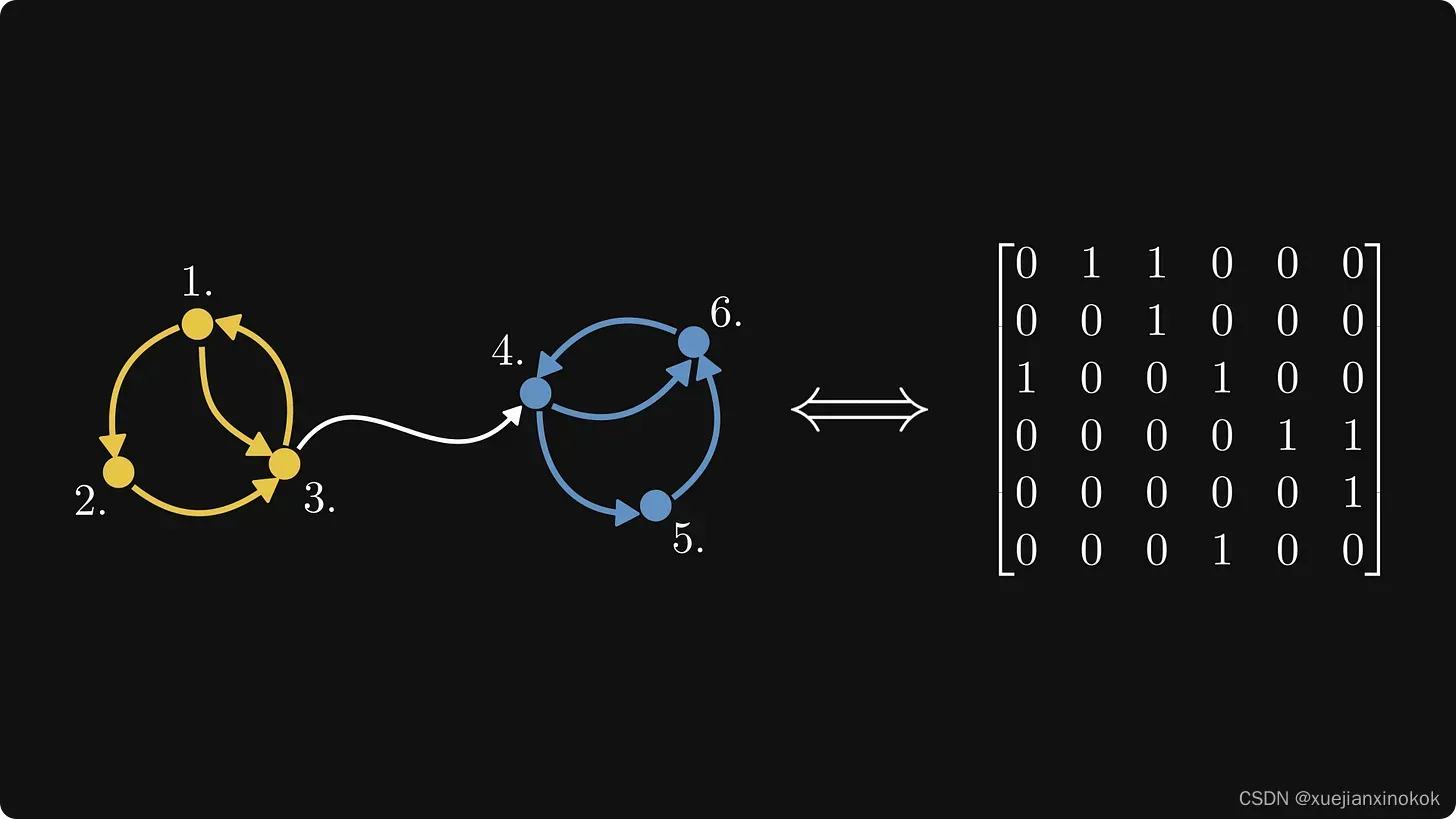
(为简单起见,假设所有边都有单位权重。)您注意到某种模式了吗?
图对应的矩阵可以简化为更简单的形式!
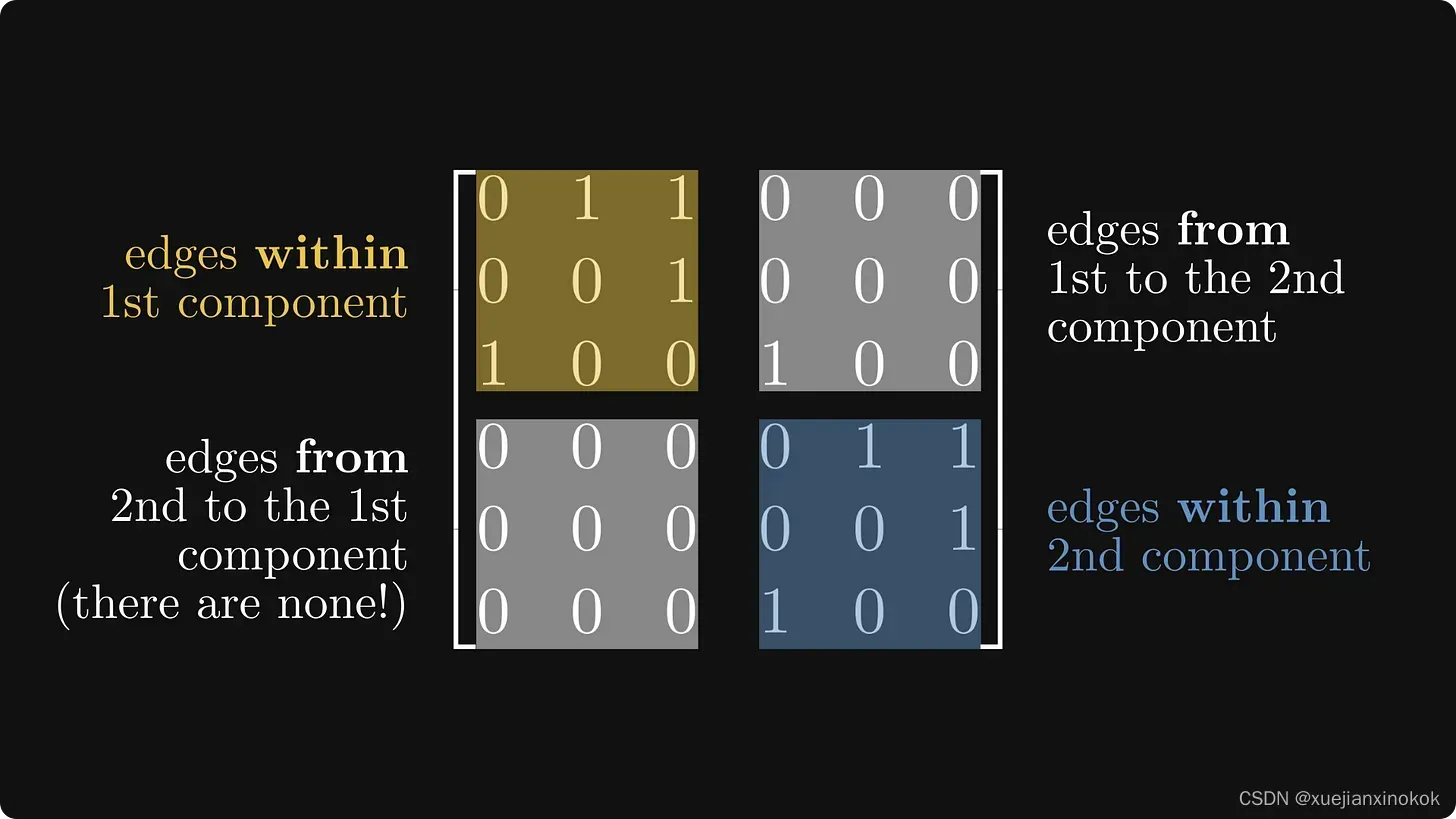
它的 对角矩阵 由图强连通的 子矩阵块组成。 (也就是说,子矩阵块是不可约的。)此外,对角线下方的块为零。
对于所有非负矩阵都是如此吗?
你猜猜。下边进入Frobenius normal form。
4. The Frobenius normal form
一般来说,我们刚刚看到的这种块矩阵结构称为Frobenius normal form。
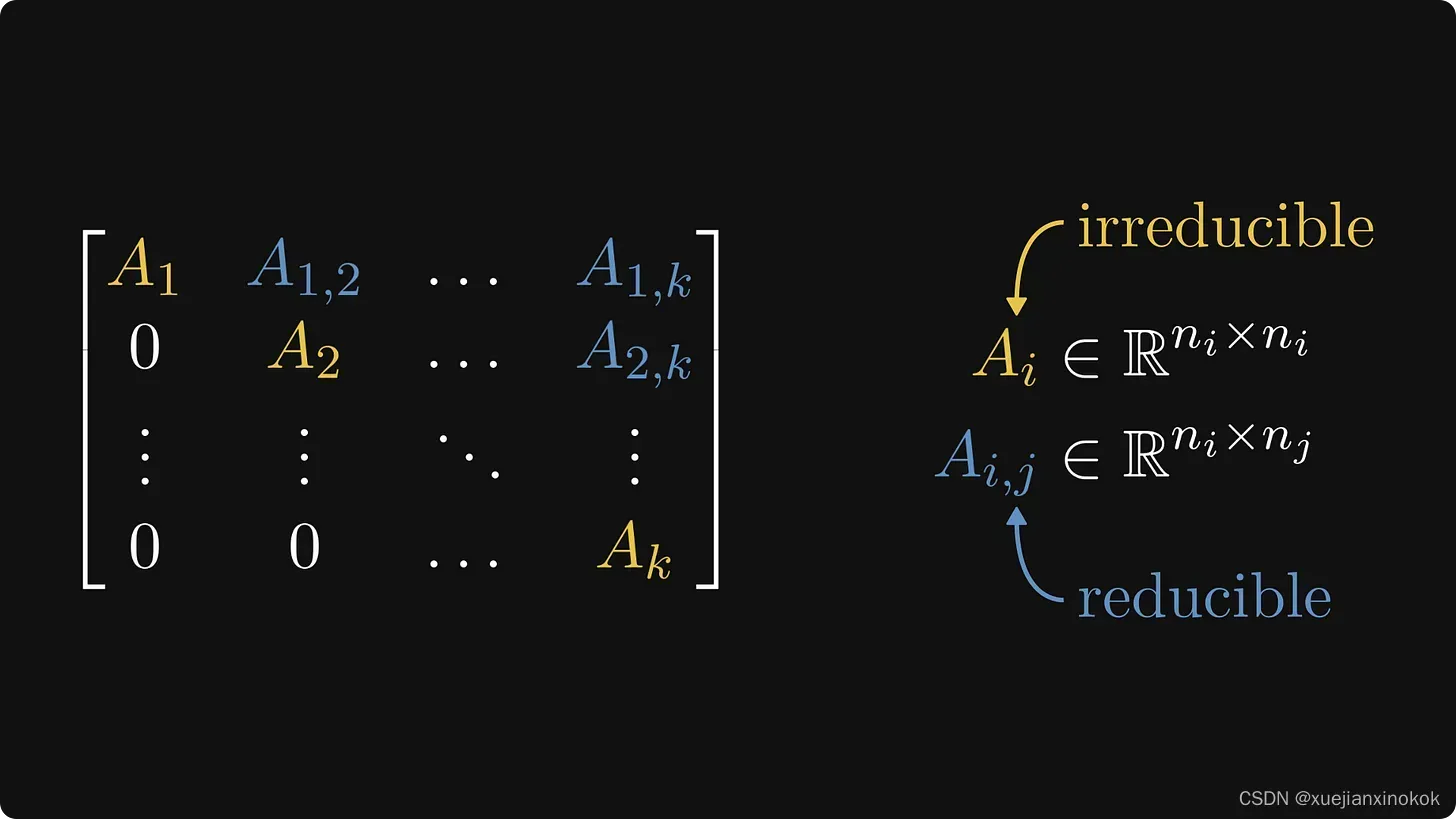
如果你的眼睛很敏锐,并且有点强迫症,你可能会注意到我稍微改变了颜色。从现在开始,不可约块(又名对应于强连接图的矩阵)将是米黄色,而可约块将是浅蓝色。
让我们把问题反过来:我们可以将任意非负矩阵转换为 Frobenius normal form?
是的,在有向图的帮助下,这比纯粹使用代数更容易显示。
这是著名定理的完整形式。

但什么是置换矩阵(permutation matrices)?
5. Permutation matrices 置换矩阵
让我们看一个特殊情况:如果我们 将 2 x 2 矩阵乘以

一个简单的零一矩阵 ?通过快速计算,您可以验证
当从左边相乘时它会切换行,
当从右侧相乘时它会切换列。
像这样:
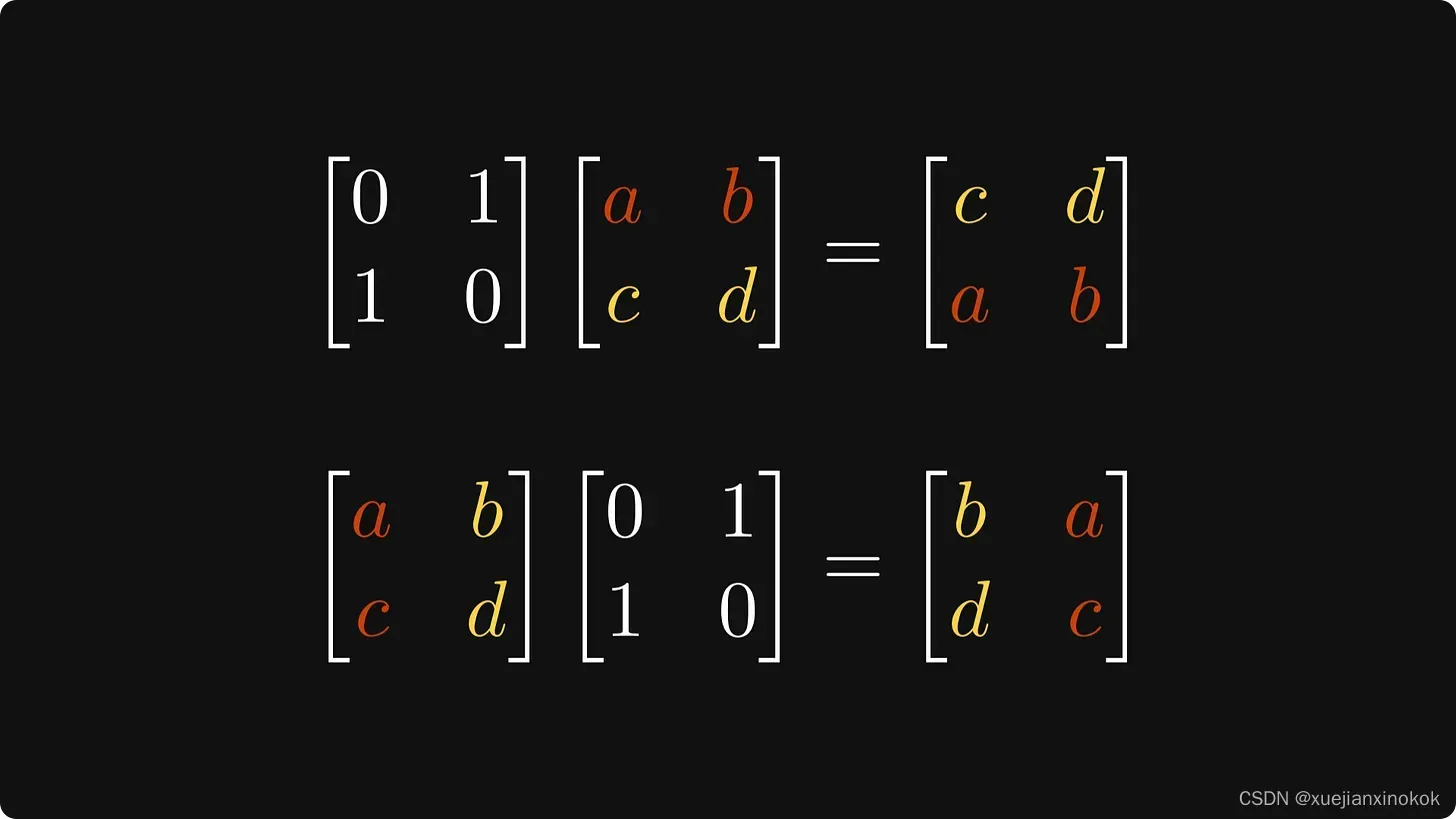
从左侧和右侧乘以 P 会产生复合效果:它会切换行和列。

(顺便说一下,这是一个相似变换,因为我们特殊的零一矩阵是它自己的逆矩阵。这不是偶然的;稍后会详细介绍。)
我们为什么要看这个?因为在幕后,这种转换(相似变换即从左侧和右侧乘以 P )不会改变底层的图结构,只是重新标记其节点!
您可以轻松地手动验证这一点,但我在下面为您可视化了它。

在一般的 n x n 情况下也存在类似的现象。在这里,我们通过交换单位矩阵的第 i 行和第 j 行来定义所谓的转置矩阵:

与转置矩阵(transposition matrix)相乘具有相同的效果:从左侧切换行,从右侧切换列。
我们不会详细说明它(因为过于复杂的符号使它特别痛苦),但您可以手动验证这确实是正在发生的事情。
这是一个简短的总结。请记下这些,因为它们很快就会变得至关重要。

对我们来说最重要的性质:使用转置矩阵(transposition matrix)的相似变换只是重新标记两个节点,但在其他方面使图结构保持不变。
现在,关于前面提到的置换矩阵(permutation matrices)。置换矩阵只是转置矩阵( transposition matrices)的乘积。

置换矩阵(Permutation matrices)从其构建块继承了一些性质。最重要的是,
their inverse is their transpose,
-
它们的逆是它们的转置,
-
它们的
相似变换只是节点的重新标记,使图结构保持不变。
要了解后一个,请考虑下面的论点。
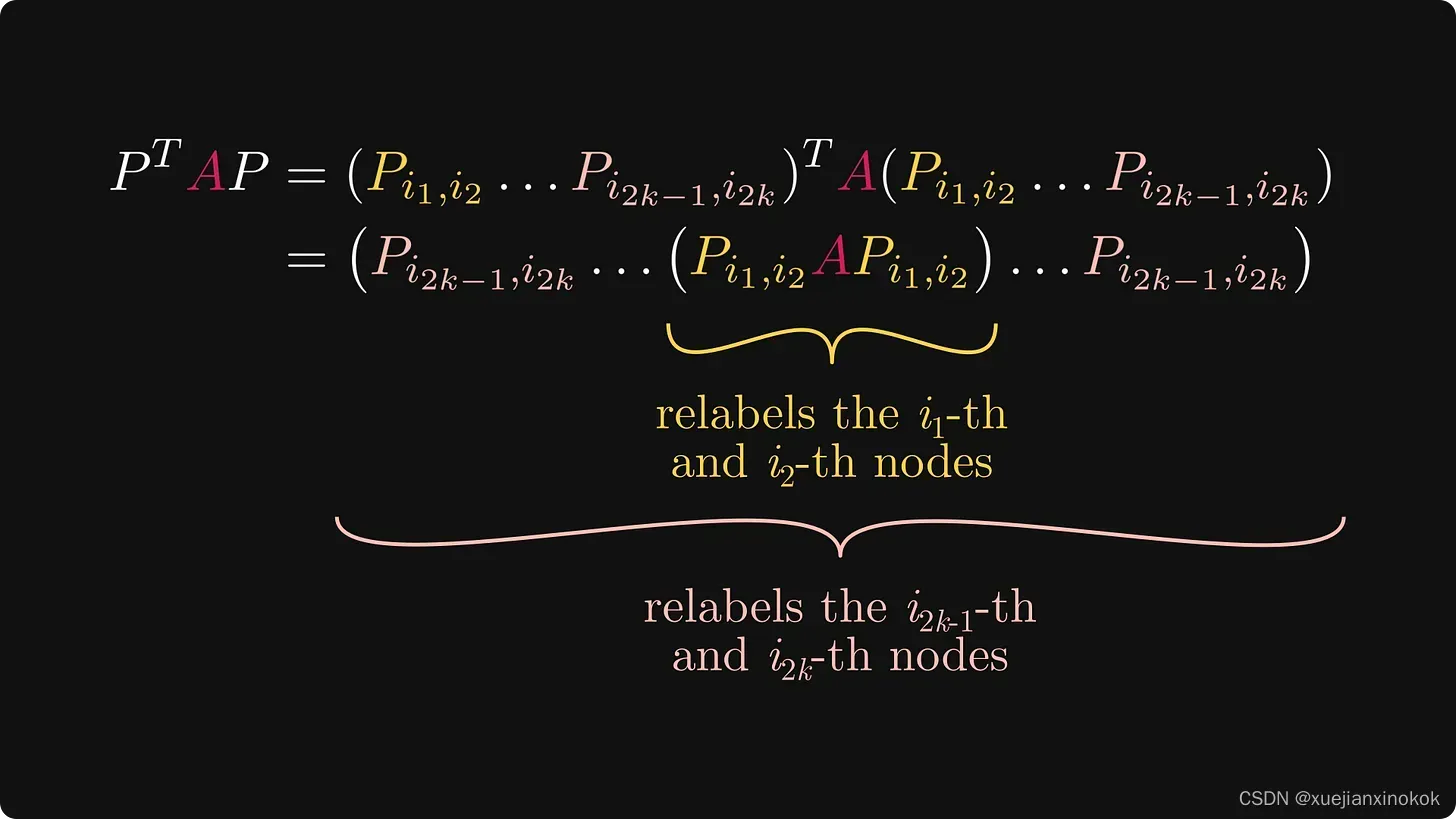
(Recall that transposing a matrix product switches up the order, and transposition matrices are their own transposes.)
(回想一下,转置 一个 矩阵乘积 会改变顺序,而转置矩阵就是它们自己的转置。)
Conversely, every node relabeling is equivalent to a similarity transformation with a well-constructed permutation matrix.
相反,每个节点重新标记相当于具有构造良好的置换矩阵(permutation matrix)的相似变换。
我们为什么要谈论这个?因为节点的正确标记是 Frobenius normal form的关键。
6. 有向图及其强连通分量(Directed graphs and their strongly connected components)
现在,我们来谈谈图。我们将看到每个有向图如何分解为强通的分量。为此,让我们看一个具体的。

这将是我们的教科书示例。
从给定节点可以到达多少个节点?不一定是全部。比如说,对于右下角的那个,只能访问图表的一部分。
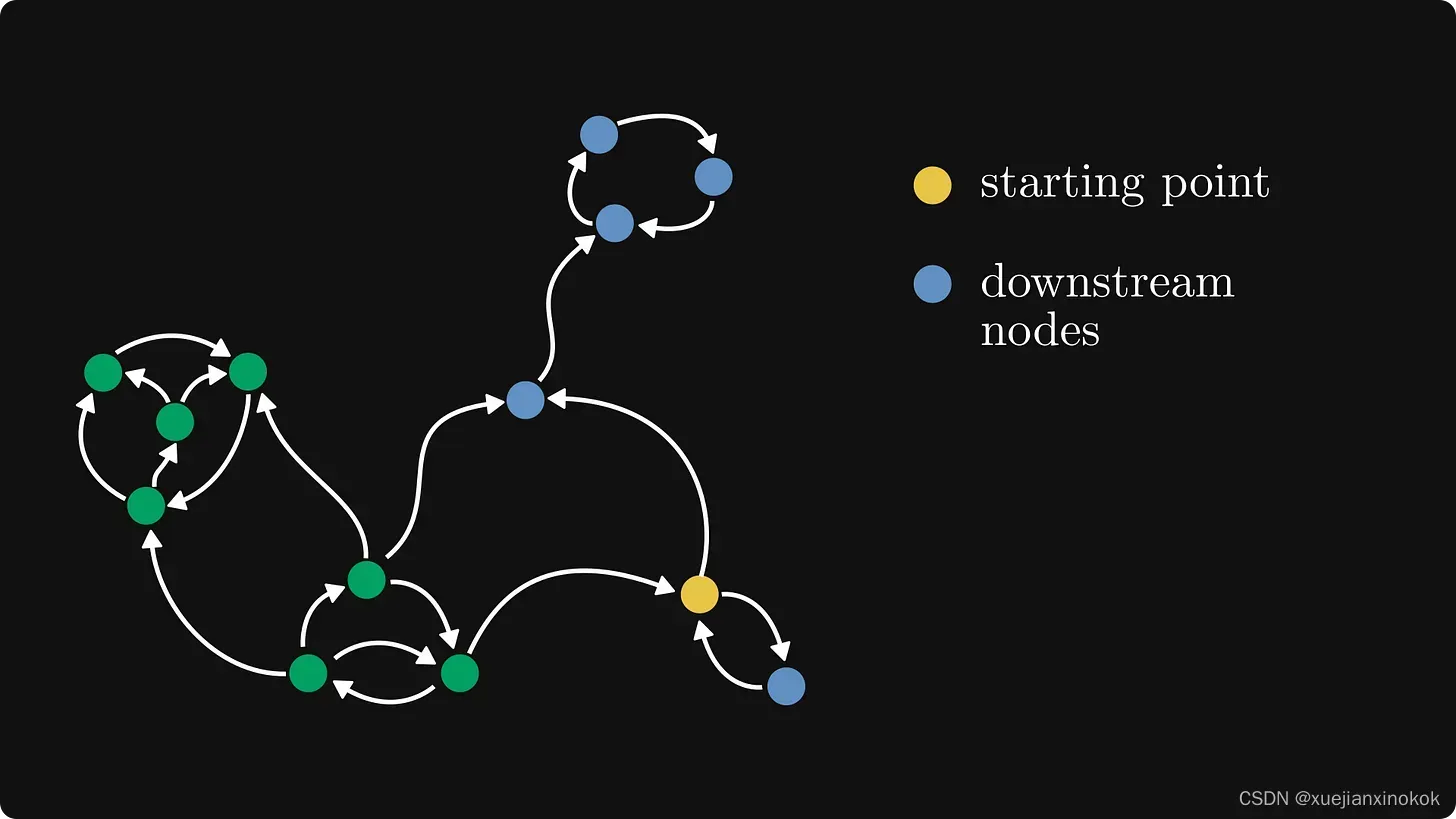
然而,相互可达的节点集要小得多。

从代数上来说,“a和b互可达”的关系是等价关系。换句话说,它将节点集划分为不相交的子集,使得
-
来自同一子集的两个节点相互可达,
-
并且来自不同子集的两个节点不能相互可达。
(等价关系是数学的主力。如果您不熟悉它们,请查看这篇关于分区的维基百科文章,了解它们之间的关系。)
该分区的子集称为强连通分量,我们总是可以用这种方式分解有向图。

现在,让我们将所有内容连接在一起! (不是以图的方式,但你知道,以健康的数学方式。)
7. 将图和置换矩阵放在一起 (Putting graphs and permutation matrices together)
我们距离证明每个非负方阵都可以通过置换矩阵变换为 Frobenius normal form还有两步。
这是计划。
-
为我们的非负矩阵构建图。
-
找到强连通分量。
-
以巧妙的方式重新标记节点。
就是这样!为什么?因为,正如我们所见,重新标记图节点与使用置换矩阵(permutation matrix)的相似变换相同。
只有一个小问题:最好的实现方法是什么?接着往下看!
首先,我们“骨架化”图:将 组件(components) 以及它们之间的任何边合并在一起。将每个 组件 视为一个黑盒子:我们不关心里面有什么,只关心它们的外部连接。

在这个骨架中,我们可以发现无法从其他组件进入的组件。这些将是我们的起点,即第零类组件。在我们的示例中,我们只有一个。
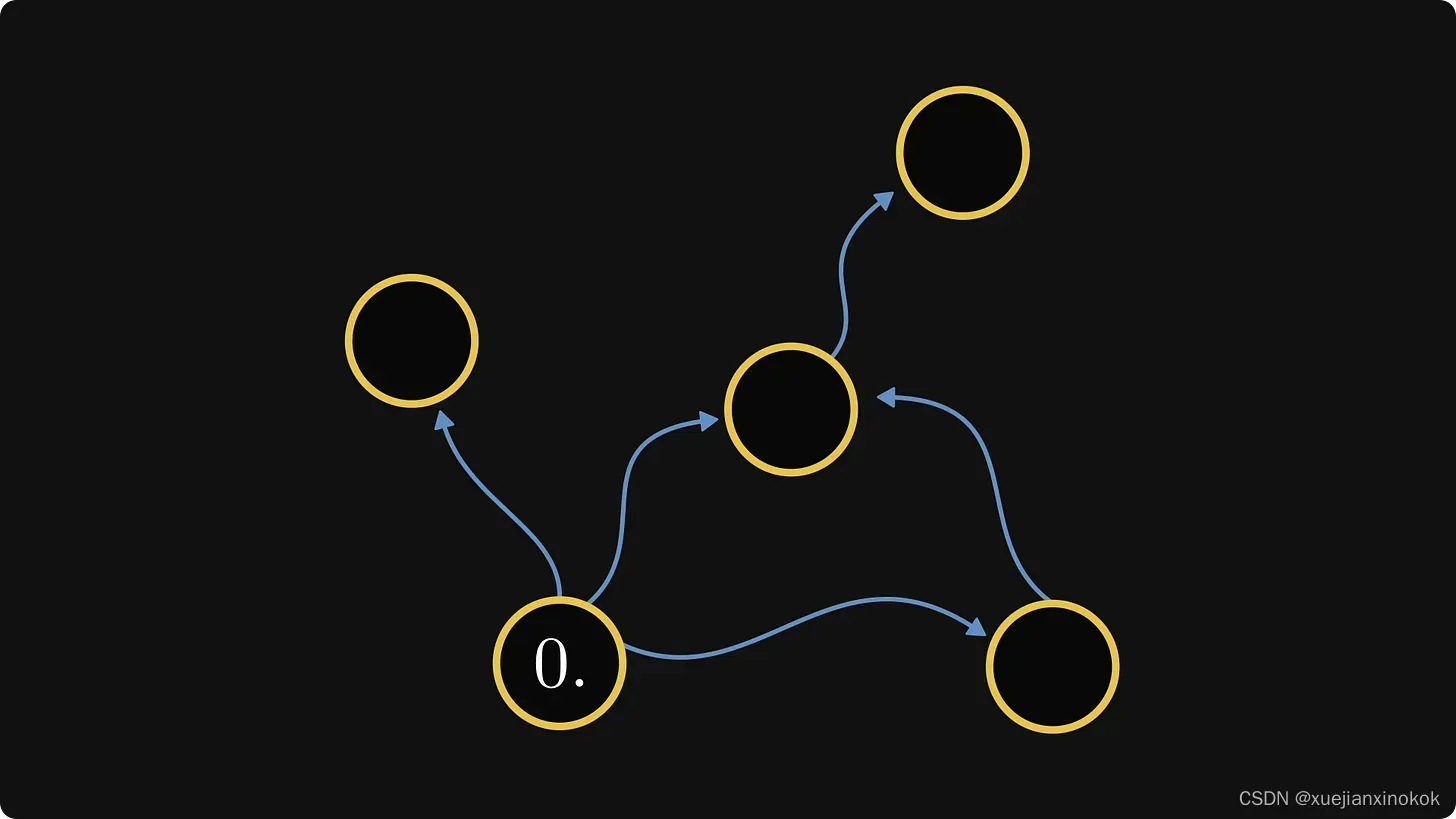
Now, things get a bit tricky. We number each component by the longest path from the farthest zero-class component from which it can be reached.
现在,事情变得有点棘手。我们按照距离最远的零类组件的最长路径对每个组件进行编号。
这甚至都很难阅读,更不用说理解了。所以,这就是发生的事情。

要点是,如果您可以从第 n 级到达第 m 级,则 n < m。
最后,我们有以下内容。
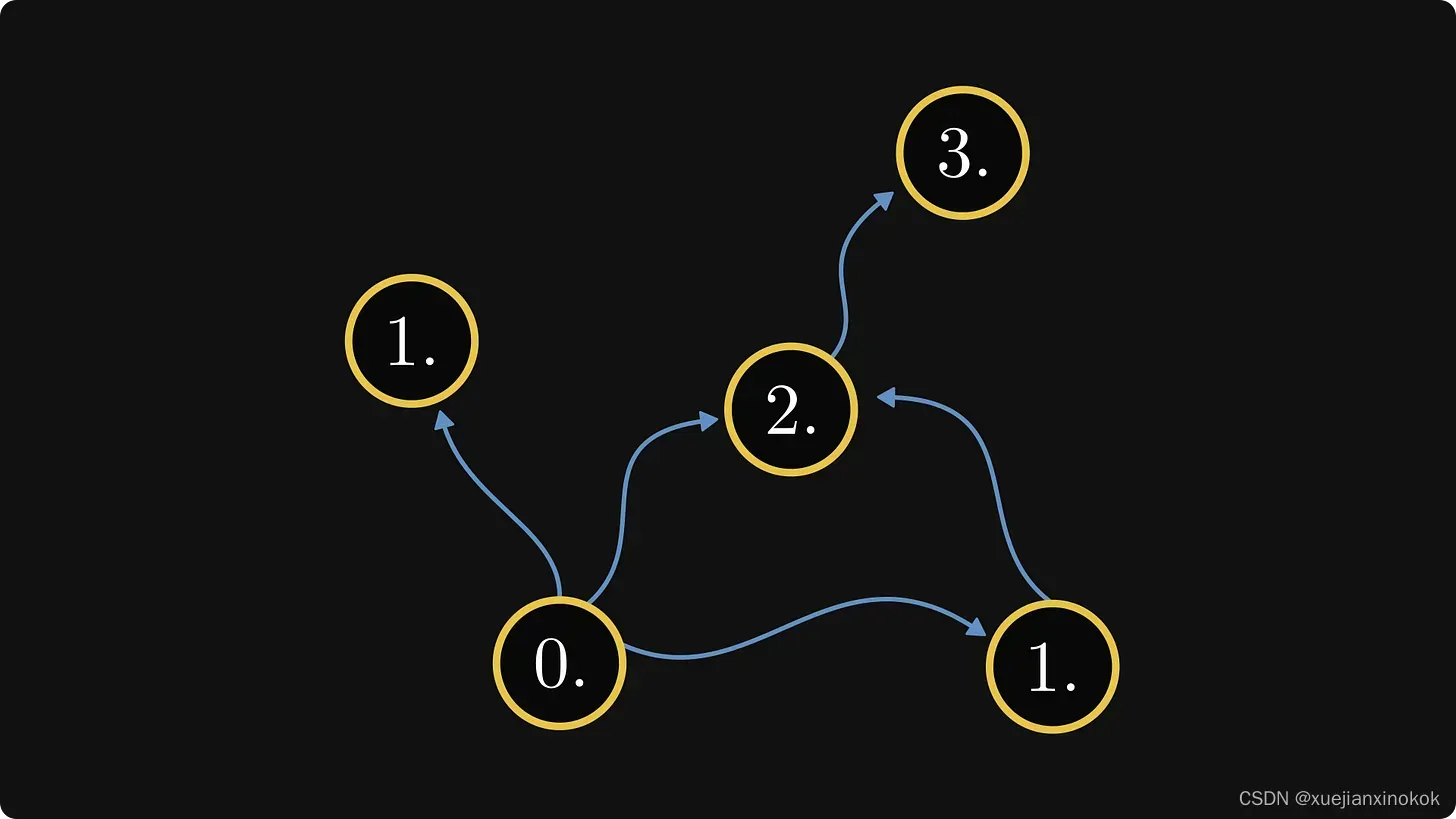
这定义了组件的顺序。 (如果您想更精确,则为部分排序。)
现在,我们标记里面的节点,这样
-
高阶类优先(higher-order classes come first,)
-
如果可能的话,连续索引是来自同一组件的标签节点。(and consecutive indices are labeling nodes from the same component if possible.)
就是这样。
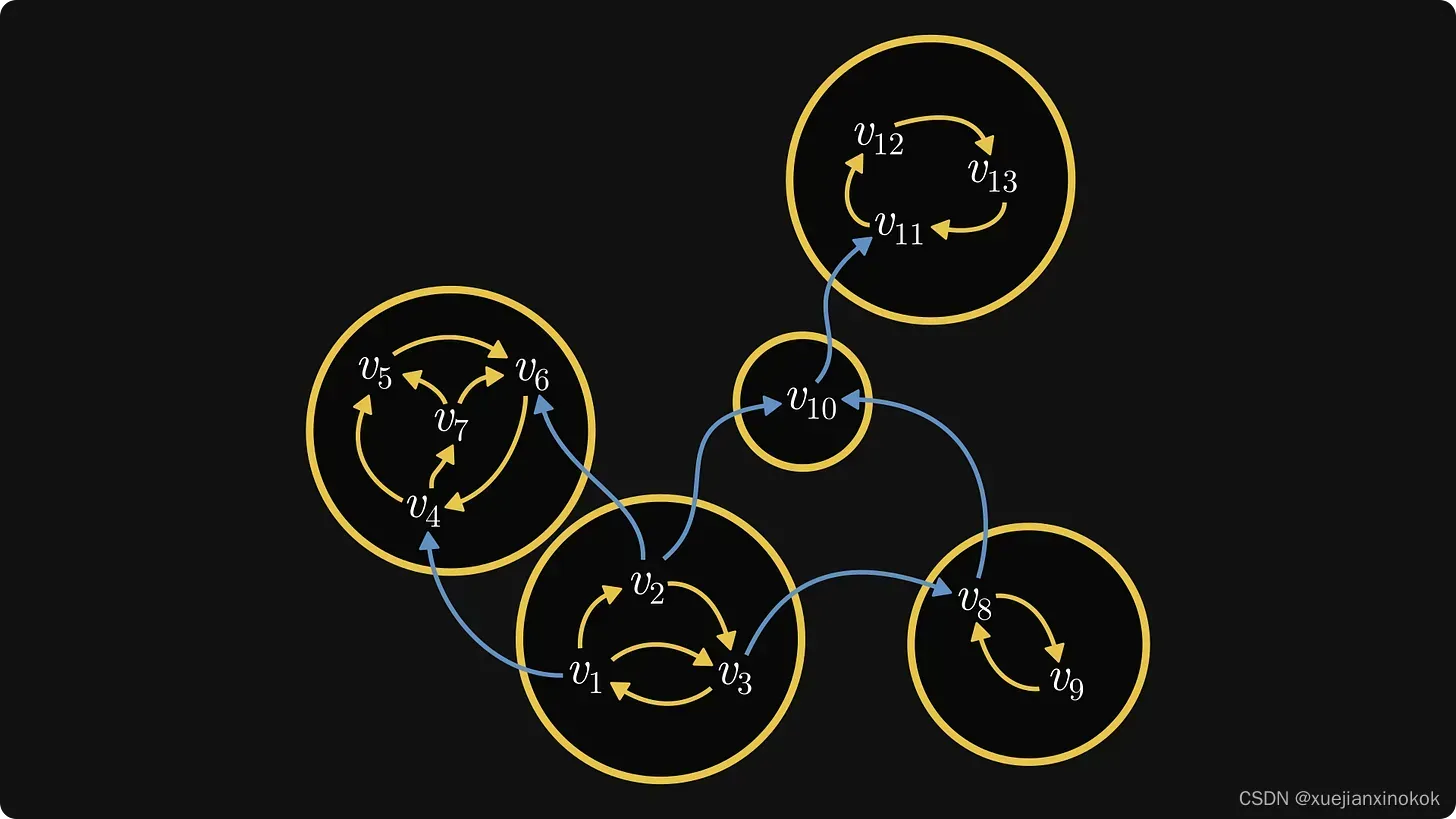
如果图本身来自实际矩阵,则这种重新标记会产生 Frobenius normal form!
下面是这个特定示例中的矩阵,为了简单起见,使用了 0 和 1:

我们巧妙标记的图的邻接矩阵
现在一切都已完成,Frobenius normal form变换背后的“证明”也完成了!
提醒您,这是该定理的完整形式:

8. 结论
我们所看到的只是冰山一角。例如,借助矩阵,我们可以定义图的特征值!这个想法催生了谱图理论这个迷人的话题,这是一个美丽的数学领域。
利用矩阵和图之间的关系对于图论和线性代数来说都是非常有利可图的。
如果你对细节感兴趣,我有两本书推荐给你。其中之一是 Richard A. Brualdi 和 Dragos Cvetkovic 撰写的精彩的《矩阵理论及其应用的组合方法》,这是我最喜欢的关于该主题的学习资源。
其次,我最近写完了机器学习的线性代数书。虽然这篇文章的内容还不是本文的一部分,但电子书格式的好处是我可以随时返回并添加新的章节。
因此,我计划将这篇文章扩展为类似教科书的章节,并可能附带交互式代码示例。如果您有兴趣,请查看我的书的前两章!
版权声明:本文为博主作者:xuejianxinokok原创文章,版权归属原作者,如果侵权,请联系我们删除!
原文链接:https://blog.csdn.net/xuejianxinokok/article/details/132357691
